谈三角形角平分线长度的处理方式

顾冬梅

[摘  要] 在高考中，时间就是分数，在确保解题正确率的前提下，解题的速度决定着整张高考试卷的得分，因此，在有限的时间内，部分压轴题的“秒杀”成为很多教师和学生研究的一项课题，也成为学生训练解题能力、突破思维断点的关键.

[关键词] 秒杀;高中数学;方法

本题以一道高考模拟题为例，呈现多种不同的解法，也深入剖析这题的科学性、严密性、价值性. 一方面以此为例，拓展我们的解题思路，引领学生发散思维的提升，启发学生站在不同的维度去分析题目的本质和内涵，也引领学生注重方法与思想的积累，在解决压轴题的过程中，达到举一反三、由此及彼的效果，引领学生敢于质疑、敢于反驳，以此促进学生的再生长.另一方面，也借此抛砖引玉，与同仁、专家一起深入研究高考题的价值与内涵，促进教师解题、讲题、命题能力的提升，进一步服务于后续教育教学质量的提升和优化，促进教师专业素养的提升.

■原题呈现

例题：在△ABC中，角A，B，C所对的边分别为a，b，c，若A=■，a=4■，角A的平分线交边BC于点D，其中AD=3■，求△ABC的面积S.

法一：（等积变形和余弦定理求两边之积）过点D向AB，AC作垂线，垂足分别为E，F.

根据角平分线性质得

DE=DF=ADsin■=3■×■=■，

根据面积公式，有

S=■bcsinA=■bcsin■=■bc，

且S=■AB·DE+■AC·DF=■·（b+c），

所以bc=3（b+c）.？摇？摇①

又由余弦定理，得

a2=b2+c2-2bccosA，

即16×7=b2+c2-bc.？摇②

联立①②，解得b+c=16，所以

S=■（b+c）=12■.

法二：（角平分线的向量表达式）根据角平分线定理得■=■=■，

所以■=■■+■■.

兩边平方，得27=■■c2+2■·bccos■+■■b2，

整理可得bc=3（b+c），以下同法一，略去.

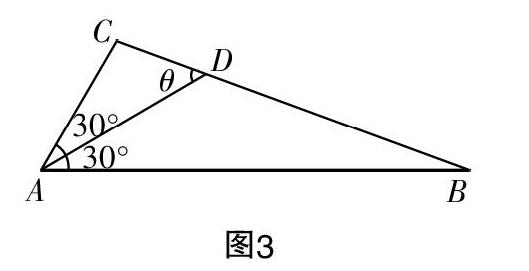
法三：（正弦定理求两已知线段的夹角）如图3所示，设∠CDA=θ.

由正弦定理可得

■=■，

■=■.

两式相加，并整理得

■=■+■=■=■=■，

即（■sinθ-2）（8sinθ+■）=0，考虑到sinθ>0，所以sinθ=■，故S=■AD·BCsinθ=■×3■×4■×■=12■.

■评价与反思

1. 对三种方法的分析

法一和法二的指导思想是一致的，既然已经知道了一个特殊角，那么就设法把这个角的夹边乘积bc求出来，而利用余弦定理和BC的长可以建立一个关于bc和b+c的关系式，那么还需要利用角平分线AD的长建立另一个关系式，法一用的是角平分线上的点到角两边的距离相等，结合等积变形建立方程，法二则是利用角平分线定理进行向量运算. 两种方法大体思路一致，手段的采取略有不同，但都值得参考.

法三和前两种方法相比有点小突破，不再盯着三角形ABC的边长，而是把原三角形看成两个小三角形拼起来的.由于这两个小三角形两个边长均已知晓，故只要求两边夹角的正弦即可，那么很自然地就利用正弦定理求解了.

2. 对解题过程的补充说明

法一对bc=3（b+c）的探究过程其实也是张角定理的推导过程（山东李振杰老师就是用张角定理快速解决了本题），张角定理内容及简证如下：

定理内容：三角形ABC中，D是边BC上一点，∠CAD=α，∠BAD=β，则■=■+■.

简证：由■AC·ABsin（α+β）=■·AB·ADsinβ+■AC·ADsinα整理即得.

法三过程中出现了sin（θ+30°）·sin（θ-30°）的形式，它可以利用下述“平方差公式”快速计算：

sin（α+β）sin（α-β）=sin2αcos2β-cos2αsin2β.

在上述的方法剖析中，我们不仅可以感受到方法的巧妙性、严密性，也反映了教师和学生在这个环节处理过程中的基本功与思维能力.在常态的教学过程中，如何促进学生思维能力的真正提升？方法有很多，一题多解、一题多变，站在不同的思维角度引领学生成长起着至关重要的作用.