数据稀缺与更新条件下基于概率密度演化-测度变换的认知不确定性量化分析

万志强，陈建兵

(同济大学土木工程防灾国家重点实验室，土木工程学院，上海 200092)

土木工程中存在诸多不确定性因素。例如，混凝土抗压强度一般存在15%~20%的变异性[1]；岩土体抗压强度参数，如黏聚力和内摩擦角，可存在20%甚至更大的不确定性[2-3]；钢筋开始锈蚀的时间，也存在显著的随机性[4]。合理表征与量化上述不确定性，是进行工程设计决策的基础。

通常，工程中的不确定性可分为固有不确定性与认知不确定性两大类。前者是由事物的客观属性决定的，这种不确定性无法降低；而后者则是由知识不完备导致的，这种不确定性将随着人们对问题认识的深入和获得信息的增加而降低[5-6]。对于固有不确定性，目前普遍采用概率论方法，即用确定性概率密度或概率分布函数描述该不确定性量[7]。而对于认知不确定性，同样可用概率的方法对其进行描述，即考虑该概率密度或分布函数是不确定的，例如其分布类型或分布参数是不定的[8-10]。Bootstrap抽样技术[2,11]和Bayes更新方法[6]为这种分布类型及分布参数的不确定性提供了可行途径。

与此相应，在工程设计中需要反映两类不确定性在系统中的传播及其对可靠性的影响。数十年来，针对固有不确定性的传播与分析问题，人们发展了Monte Carlo方法[12]、随机摄动方法[13]、正交多项式展开理论[14]和概率密度演化理论[15]等多种方法。近年来，为了进一步提升效率，各种代理模型方法的研究得到了高度重视[16]。工程实际问题中，固有不确定性与认知不确定性往往是耦合的。上述方法原则上可以用于同时存在两类不确定性的问题。例如，唐小松等[2]基于Bootstrap方法、采用Monte Carlo模拟对由于数据稀缺导致存在认知不确定性时的边坡可靠度进行了分析。但在上述方法中，通常需要两重迭代，因而计算工作量极大[2,8-9]。最近，Chen和Wan[17]结合概率密度演化理论与概率测度变换(PDEM-COM)，提出了统一处理两类不确定性的逻辑框架，对于具有认知不确定性和固有不确定性耦合的不确定性量化与传播问题发展了高效分析策略。

在上述研究工作的基础上，本文基于工程实测数据，首先分别引入Bootstrap方法和Bayes更新方法进行认知不确定性表征。在此基础上，结合PDEM-COM方法，给出了基于数据进行工程系统不确定性量化、传播与可靠性分析的基本途径与数值方法。实例分析表明，本文建议方法具有很高的精度和效率，便于实际工程应用。

1 两类不确定性的表征方法

不失一般性，记系统响应为：

式中：Θ为模型的不确定性参数；Λ为确定性参数；f(·)为线性或非线性算子。进一步，记具有固有不确定性的参数为ΘAU，具有认知不确定性的参数为ΘEU，则有：Θ=(ΘAU,ΘEU)T，或

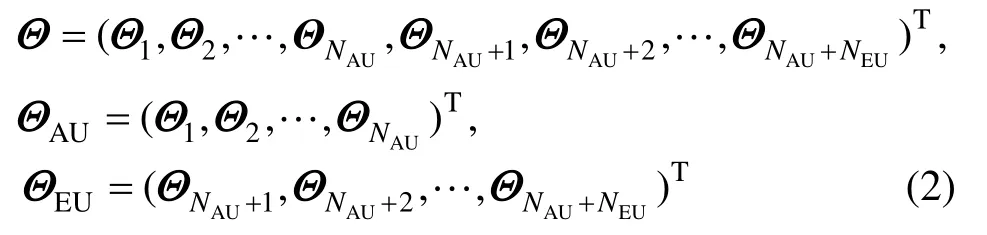
即有NAU个固有不确定性参数、NEU个认知不确定性参数。

在本文中，考虑一类重要的认知不确定性来源，即固有不确定性参数ΘAU的概率分布具有不确定性[1,8]。例如，在岩土工程中，由于试验数据十分有限，导致边坡可靠度分析所需的工程抗剪强度参数的分布参数变异性极大，这是分布参数不确定性的体现[2-3]；在结构工程中，混凝土抗压强度的试验数据可能同时通过正态分布和Weibull分布的假设检验[18]，这是分布类型不确定性的表现。上述概率分布的不确定性，可通过Bootstrap方法和Bayes更新方法进行表征和量化，详述如下。

1.1 Bootstrap方法

Bootstrap方法[10]是对原始试验数据进行有放回随机抽样、以获取分布参数不确定性信息的方法。当实测数据较为稀缺时，该方法是量化认知不确定性的有效途径[2]。

例如，假定原始试验数据为D=(θ1,θ2,…,θn)，进行K次Bootstrap抽样后可得：

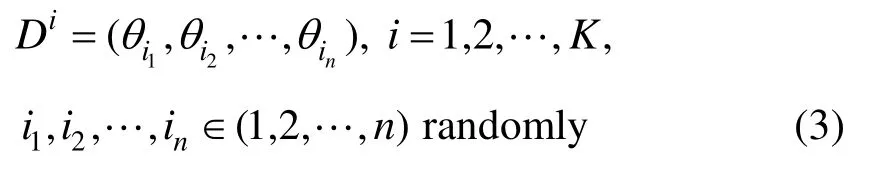
若仅根据原始数据D进行统计分析，可以得到前二阶矩估计值，即均值μΘ和标准差σΘ。通过Bootstrap抽样技术，可进一步获得一系列矩估计值当随机变量Θ的分布类型确定时，Bootstrap提供了表征分布参数认知不确定性的途径。此时，随机变量Θ的概率描述不再是唯一的概率密度函数pΘ(θ,μΘ,σΘ)，而变为概率密度函数族相应地，工程结构或系统分析模型的输出量X不再具有唯一确定的概率密度函数，而是对应的概率密度函数族在第2节中，将详细阐述如何在不显著增加计算成本的前提下，进行上述不确定性的量化。

1.2 Bayes更新方法

另一种可能的工程情况是：在结构设计阶段，通过现场实测得到一批试验数据，需要对设计参数进行更新[19]；或在工程监测时获得一批新的实测数据，需要对设计阶段的分析结果进行验算。这两种情况可统一为如下表述：

记随机变量Θ的原始观测数据集为D1、新增观测数据集为D2。同时，记由数据D1通过统计推断得到的概率密度函数为其中ζ1为由数据D1统计推断得到的分布参数。若考虑Θ的推断过程中存在认知不确定性，即ζ1本身是不确定性的。在一般情况下，ζ1的先验分布pζ(ζ)是人为假定的。事实上，根据1.1节的讨论，该先验分布可基于Bootstrap方法给出。当引入新增数据D2后，通过Bayes更新方法，可得参数的后验分布：

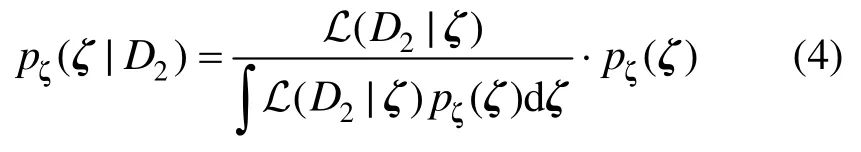
其中，L(·)为极大似然函数，有：

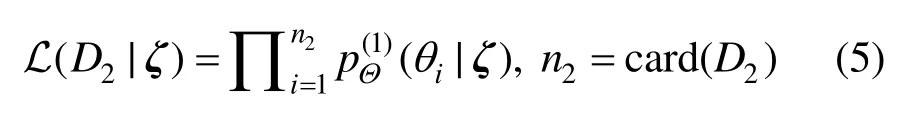
式中，card(·)表示集合中的元素个数。由式(4)和式(5)可得：

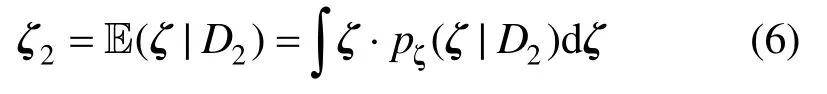
由此，随机变量Θ的概率密度函数由pΘ(θ|ζ1)更新为pΘ(θ|ζ2)。此时，工程模型输出对应的概率分布亦应由更新为这一更新过程，可通过下节介绍的高效方法完成。

2 概率密度演化与概率测度变换

本节将简述概率密度演化理论(PDEM)与概率测度变换(COM)的基本原理。在此基础上，介绍固有不确定性与认知不确定性同时存在的情况下不确定性量化与传播的PDEM-COM统一理论框架。

2.1 概率密度演化理论(PDEM)

不失一般性，考虑随机微分方程：

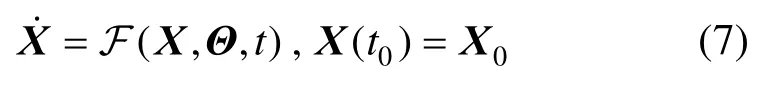
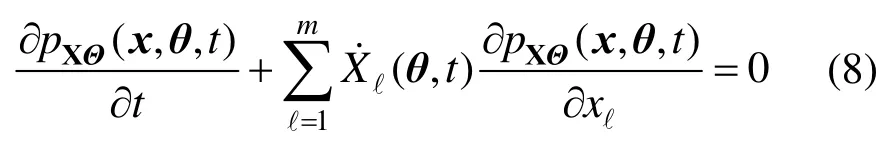
其中，pXΘ(x,θ,t)为(X,Θ)的联合概率密度函数。相应的初始条件为：

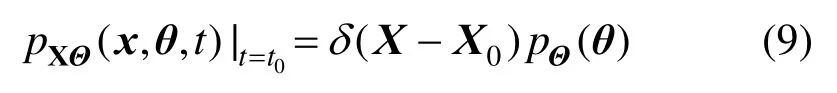
式中，δ(·)为Dirac函数。求解式(8)并对Θ积分可得：

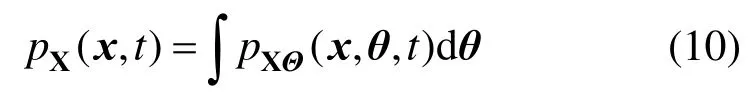
求解方程组式(7)~式(9)的数值算法如下[20]：

1) 对概率空间ΩΘ进行剖分，记剖分子域为：

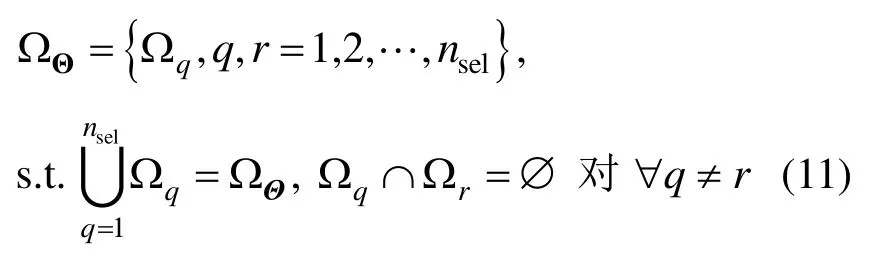
由此，可获得对应的代表点Θ=θq,q=1,2,…,nsel及其对应的赋得概率：

其中，nsel为代表点个数。本文采用使得GF-偏差最小化[21]的点集优选策略获得上述代表性点集。

2) 对每一个代表点求解物理方程式(7)，获得速度状态量

3) 对每一个代表点求解如下概率密度演化方程：

4) 累计求和：

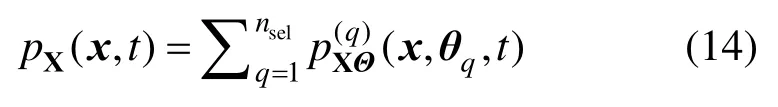
由此，一旦给定一组系统输入Θ的概率信息pΘ(θ)，通过上述概率密度演化理论可十分方便地获得相应的系统输出概率信息pX(x)。

2.2 概率测度变换(COM)

考虑μ和ν是σ-有限测度，且定义于可测空间(ΩΘ,F)；若ν相对于μ绝对连续，则存在可测函数T :ΩΘ→[0,∞)，使其满足[22]：

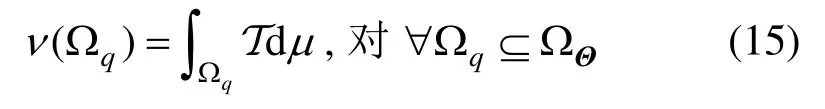
式中，函数T=dν/dμ称为Radon-Nikodym导数。换言之，不同测度之间可以通过算子T进行变换，而不需要引入额外计算工作量。

基于此，当同时存在固有不确定性与认知不确定性时，Chen和Wan[17]结合概率密度演化理论(PDEM)与概率测度变换(COM)，提出了一类不确定性量化与传播的高效方法(简记为PDEM-COM)，其算法如下：

1) 给定一组概率信息pΘ(θ)，进行一轮PDEM分析。分析时，储存代表性点集及速度状态量和pX(x,t)。当研究的是静力分析问题时，可采用等价极值分布方法[23]。

4) 重复步骤2)~3)，直至所有需要重新量化的认知不确定性完成不确定性传播过程。

注意到，在PDEM-COM中，仅在第一轮概率密度演化分析中进行确定性物理过程分析(一般为300次~500次左右)。在随后的认知不确定性量化分析过程中，将集中于测度变换的计算(新的赋得概率)。此时，与复杂物理系统确定性分析的计算成本相比，新增的计算工作量很小。而且，物理系统越复杂，这一优势越明显。

3 工程算例

3.1 无限边坡稳定分析模型

考虑一个无限边坡稳定分析模型[2]，如图1所示，其极限状态方程为：

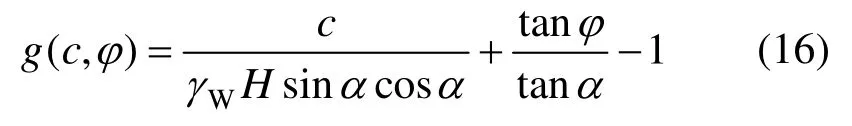
取边坡几何参数H=5m和α=30°，土体重度γW=17kN/m3。抗剪强度参数c和φ分别代表土体有效黏聚力和有效内摩擦角，分别服从对数正态分布和正态分布。

抗剪强度参数的试验数据往往不易获得，如文献[2]仅给出了24组观测值。唐小松等[2]根据这24组观测值，采用Bootstrap方法考察了抗剪强度参数分布的两类认知不确定性，并给出了边坡可靠度在这两类不确定性下的可靠度指标量化范围。文献[2]同时还指出，该分析需要与Bootstrap抽样次数等量的可靠度计算次数，因此对于复杂的边坡可靠度分析问题而言，这种需要进行双重循环的认知不确定性分析方法计算工作量巨大。

根据第2节的基本理论，对认知不确定性分析，可采用如下流程：

1) 令原始数据集为D=(ci,φi),i=1,2,…,n，本例取n=24；定义Bootstrap子样本为Dj,j=1,2,…,B，其中B为Bootstrap抽样次数，本例取B=104。

2) 由Bootstrap方法对24组观测值进行认知不确定性度量，即给出抗剪强度参数c和φ的均值μc和μφ、标准差σc与σφ的Bootstrap分布及其95%置信区间(表1)，下横线对应区间下限值，上横线对应区间上限值，即：

3) 基于概率密度演化理论，以下列分布参数进行一次可靠度分析[16,20-21,23]：

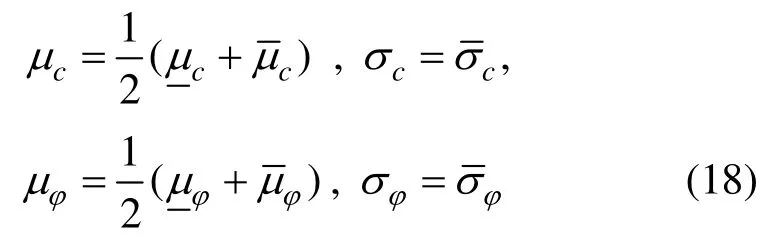
4) 针对每一个Bootstrap子样本Dj计算统计量并计算对应的测度变换算子

5) 由3)得到的概率密度演化分析结果，结合4)计算得到的测度变换算子，给出每个Bootstrap子样本对应的概率密度演化分析结果。这里的概率密度演化分析结果，可以是响应的一阶、二阶矩信息，亦可是可靠度指标信息，由问题本身确定。在本例中，考虑边坡可靠度指标，即：

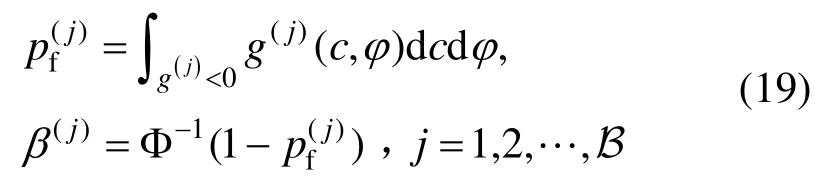
式中，Φ(·)为标准正态分布的分布函数。

由此可得到存在认知不确定性的情况下的边坡可靠度指标β={β(j),j=1,2,…,B}及其5%分位值和95%分位值，如图2所示。为验证本方法的计算精度，采用500万次Monte Carlo模拟求解本例的可靠度分布，如图3所示。从图2与图3的对比中可见，不仅可靠指标分布直方图总体形状一致，而且相应的均值与分位值均具有很高的计算精度。特别指出，在PDEM-COM中，仅需要进行一轮完整的概率密度演化分析，因而全部分析中仅需要进行500次确定性分析。

表1 由Bootstrap方法给出的95%置信区间(例3.1)Table 1 95% confidence interval by Bootstrap (E.3.1)

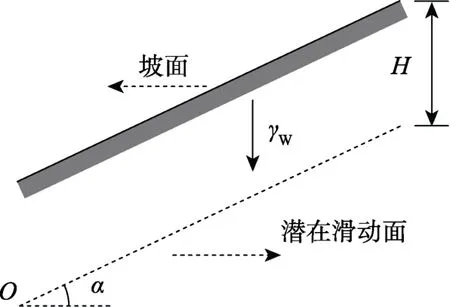
图1 无限边坡稳定分析模型[2]Fig.1 Infinite slope model for stability analysis[2]

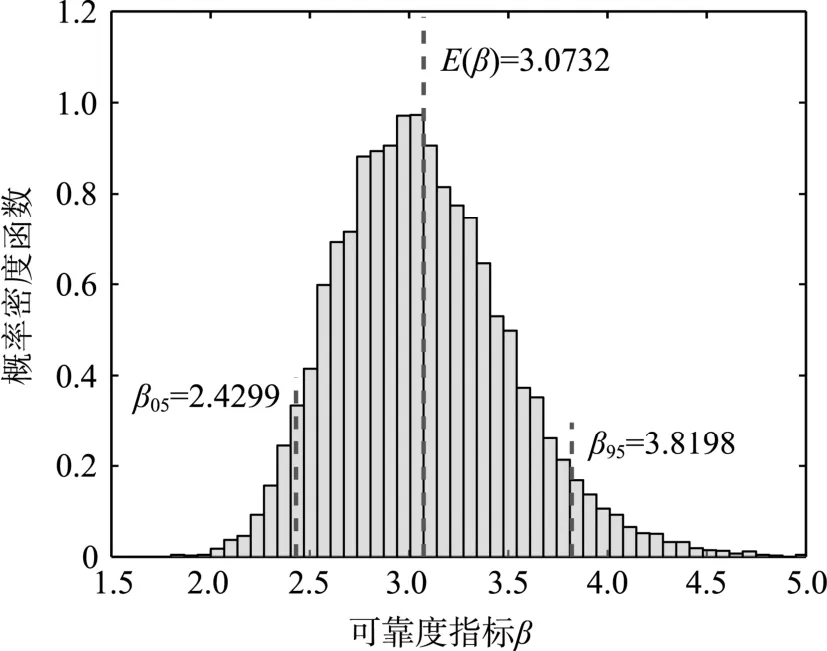
图2 边坡可靠度指标的Bootstrap分布(PDEM-COM)Fig.2 Bootstrap distribution of reliability index of infinite slope model (PDEM-COM)

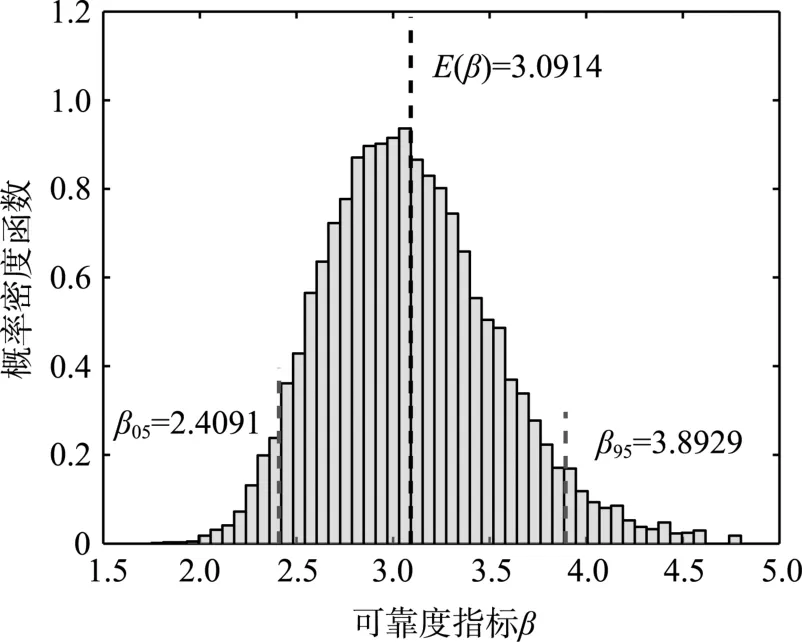
图3 边坡可靠度指标的Bootstrap分布(5×106 MCS)Fig.3 Bootstrap distribution of reliability index of infinite slope model (5×106 MCS)

3.2 挡土墙稳定性分析模型

考虑挡土墙稳定性分析模型[3]，如图4所示。在承载力满足的情况下，该模型可能存在两种失效模式，其对应的功能函数分别为：

1) 滑移破坏模式

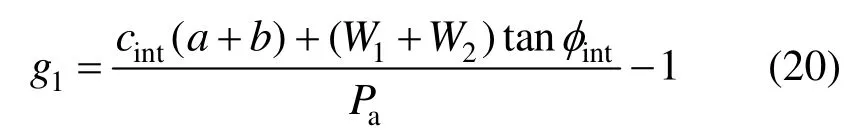
式中：cint=1/3·cb和φint=2/3·φb分别为接触面处的粘聚力和内摩擦角，cb和φb是对应地基处的粘聚力与内摩擦角；Pa为主动土压力(忽略墙体表面裂缝影响)，有：

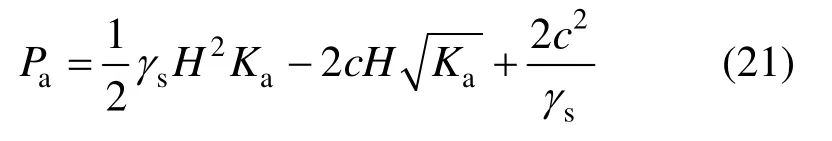
式中，Ka为主动土压力系数，由Rankine理论给出：

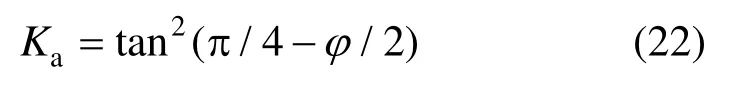
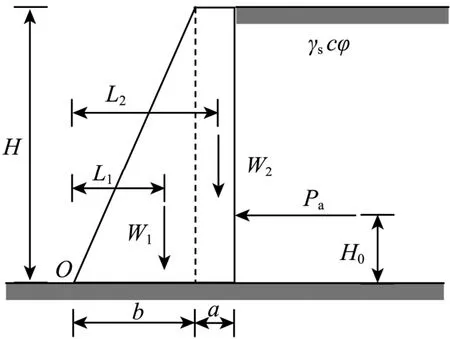
图4 挡土墙稳定性分析模型[3]Fig.4 Stability analysis model of retaining wall[3]

式(20)~式(22)其他参数取值及定义详见表2。

表2 挡土墙稳定性分析模型参数(例3.2)Table 2 Model parameters of retaining wall (E.3.2)

2) 倾覆破坏模式

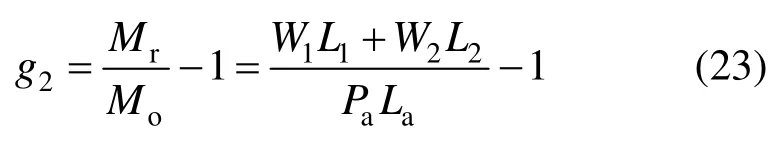
其中，L1、L2和La分别取为：

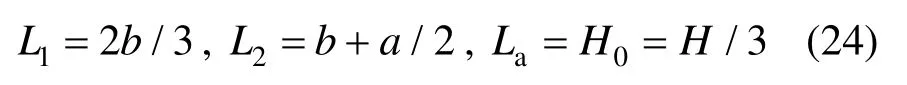
显然，两种失效模式均为有效粘聚力c与有效内摩擦角φ的函数。文献[3]提供了63组固结排水情况下的抗剪强度参数试验数据，本节将利用该数据考察认知不确定性对挡土墙稳定性分析的影响。

3.2.1 情况1：由Bootstrap方法度量认知不确定性

首先考察数据样本大小带来的认知不确定性。记该63组数据的前30组数据为D1(数据集1)，全部数据为D2(数据集2)。同样地，由Bootstrap方法可给出抗剪强度参数c和φ的均值μc和μφ及标准差σc和σφ的Bootstrap分布及其95%置信区间，见表3所示。将8组置信区间绘制于图5可见，在样本量较小时置信区间范围也较大，扩大样本量确能缩小该不确定性范围；二阶统计矩的缩小程度要比一阶统计矩大。

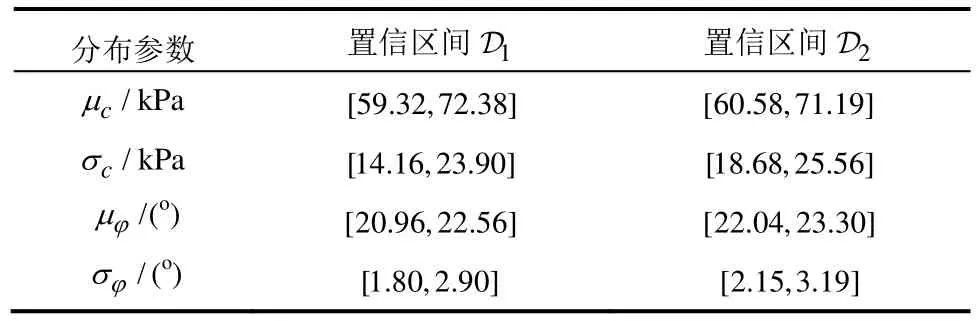
表3 由Bootstrap方法给出的95%置信区间(例3.2.1)Table 3 95% confidence interval by Bootstrap method(E.3.2.1)

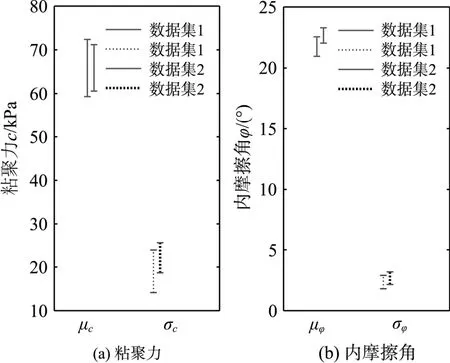
图5 两组数据集给出的Bootstrap分布的95%置信区间Fig.5 95% confidence intervals of two data sets by Bootstrap method

由数据集D1和D2给出的挡土墙可靠度的Bootstrap分布如图6和图7所示。可以看到，当认知不确定性较大的时候(如数据集D1相对于数据集D2)，其可靠度指标的变化范围也较大。需要注意的是，当增加统计样本数量以减少认知不确定性时，可靠度指标的不确定性范围虽然随之变窄，但其期望值却下降了。这说明，若不考虑该认知不确定性带来的影响，如将可靠度指标的期望作为最终分析评估的结果，将使得分析结果偏于不安全。因此，有必要根据实际工程案例进行认知不确定性量化工作。

3.2.2 情况2：由Bayes更新度量认知不确定性

首先由数据集D1给出抗剪强度参数c和φ的分布参数(先验概率密度函数)，然后通过额外数据集(算子⊖代表取差集)对进行更新，可得到(后验概率密度函数)。特别地，若考虑用所有已知数据D2进行参数识别，亦可得到对应的(全信息概率密度函数)。图8给出上述三种情况对应的概率密度函数。在PDEM-COM分析中，以为分析工况进行一次概率密度演化分析即可，而的情况用测度变换方法给出，由此给出的可靠指标如表4所示，括号中数值为采用100万次MCS直接模拟得到的结果。从表中可见，采用PDEM-COM可以得到精度很高的可靠指标估计结果。

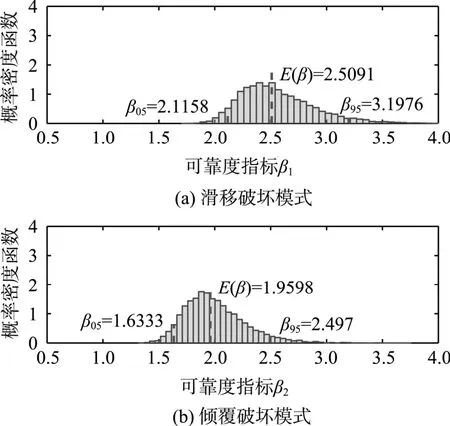
图6 由数据集D1得到的两种失效模式的可靠度分布Fig.6 Distributions of reliability index of two failure modes by data set D1

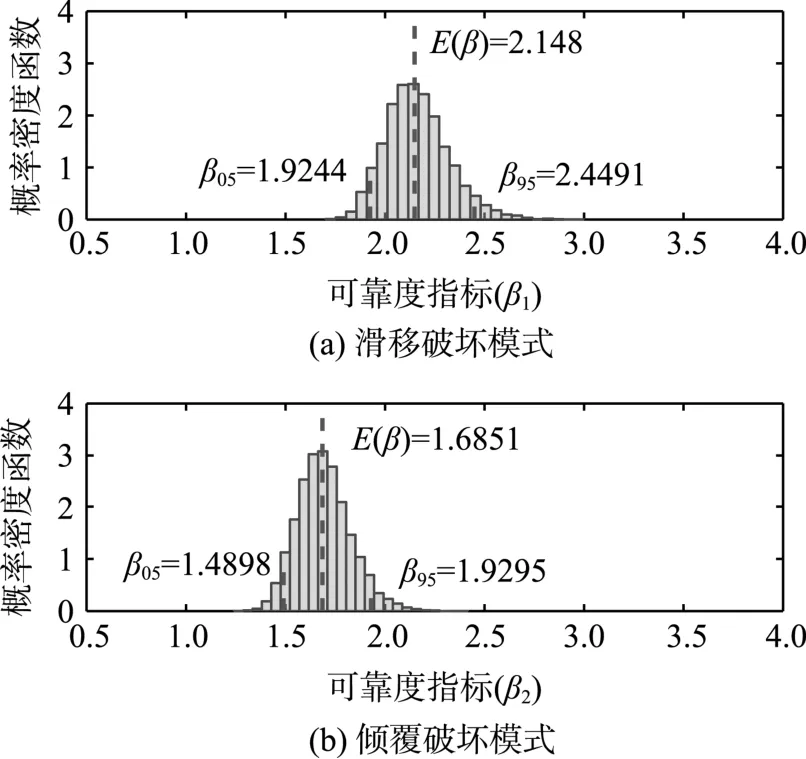
图7 由数据集D2得到的两种失效模式的可靠度分布Fig.7 Distributions of reliability index of two failure modes by data set D2

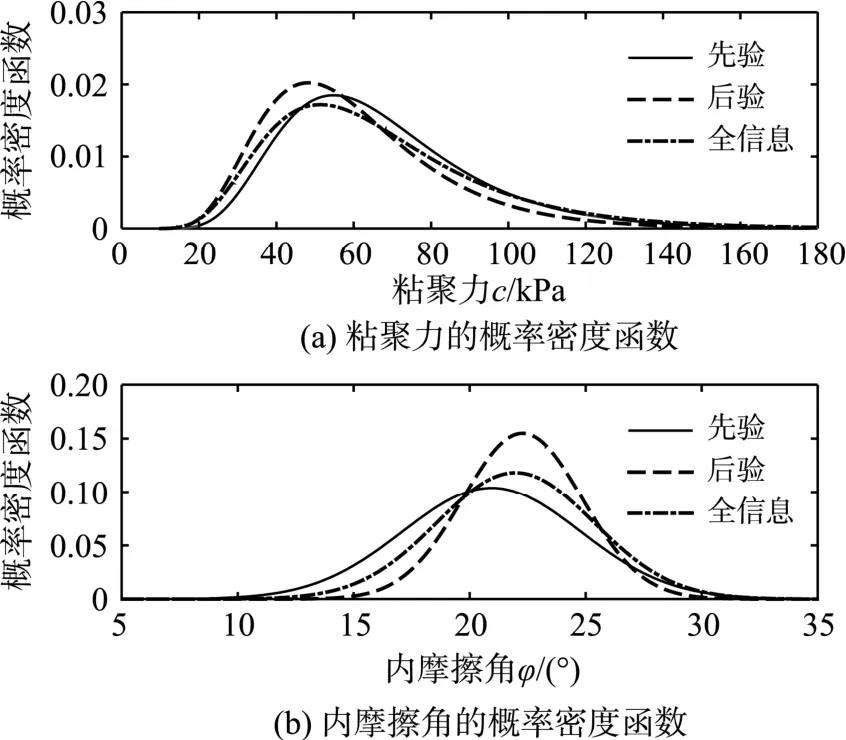
图8 三种情况下抗剪强度参数的概率密度函数Fig.8 PDFs of shear parameters on three conditions

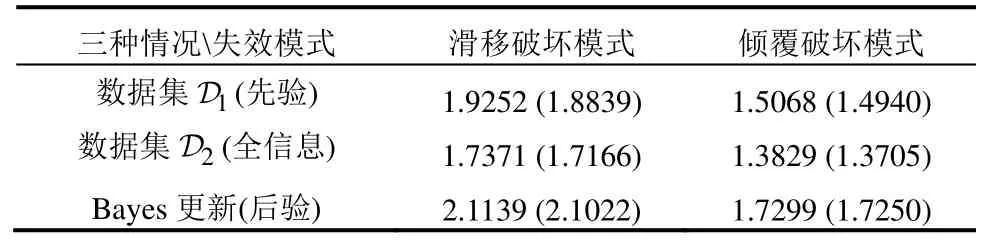
表4 两种失效模式的可靠度指标(例3.2.2)Table 4 Reliability indexes of two failure modes (E.3.2.2)

3.3 屋面桁架结构

考虑一个屋面桁架结构[24](如图9所示)，其功能函数定义为：

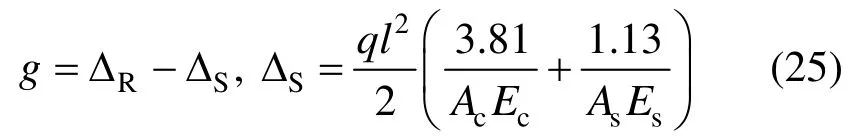
式中：q为均布荷载，简化为三个集中力P=ql/4；Ac和As分别为混凝土构件与钢构件的截面积；Ec和Es分别为混凝土材料与钢材的弹性模量值；ΔS为屋顶竖向位移；极限变形位移取ΔR=l/400。

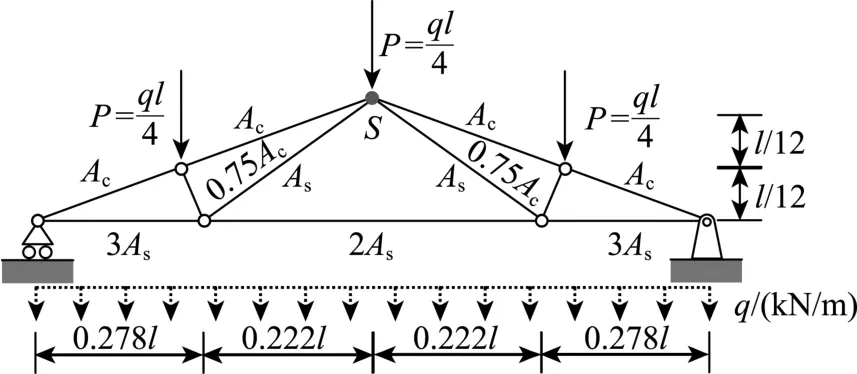
图9 屋面桁架结构[24]Fig.9 Roof truss structure[24]

本节考察认知不确定性与固有不确定性同时存在时对结构可靠性分析的影响。若进行结构弹性位移下的可靠度分析(关于杆件内力可靠度分析可详见文献[25])，可考虑混凝土弹性模量与截面积存在不确定性，其他设计参数均为确定性的。进一步，由于既有试验数据有限，考虑混凝土截面积的不确定性仅为固有不确定性，即服从给定的概率分布；而混凝土弹性模量则同时存在认知不确定性和固有不确定性，即其概率分布是不确定性的，由既有试验数据并结合Bootstrap抽样技术进行表征。本例取文献[26]给出的100组商品混凝土弹性模量试验值，将其分为数据集D1(前30组数据)和数据集D2(所有数据)两部分，分别进行Bootstrap分析，数据分析结果如图10所示。

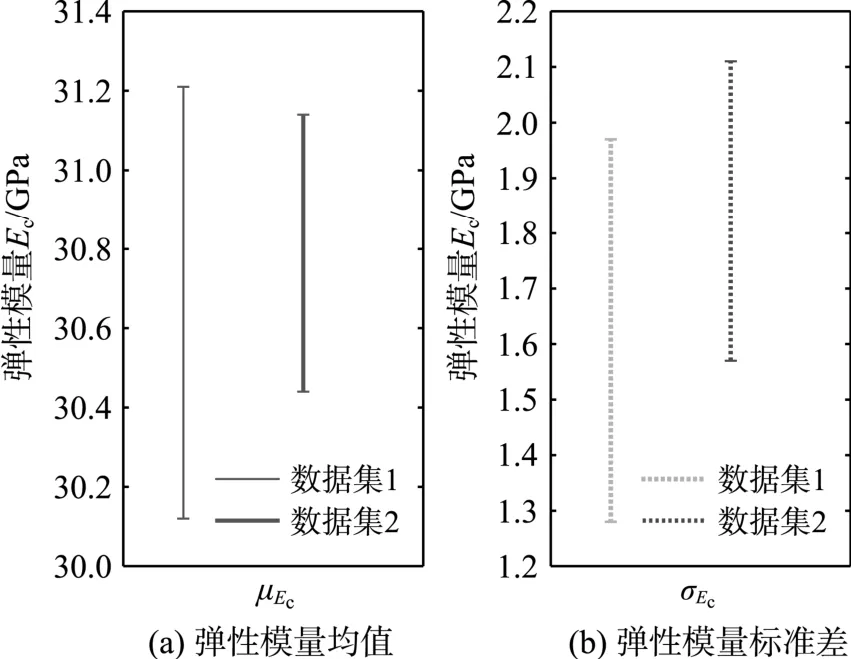
图10 两组数据集给出的Bootstrap分布的95%置信区间Fig.10 95% confidence intervals of two data sets by Bootstrap method

从图中可见，增大样本数量降低了不确定性的变化范围，这与图5中的特征是一致的。本例中的结构分析参数详见表5和表6。

表5 屋面桁架结构确定性参数(例3.3)Table 5 Deterministic parameters of roof truss model (E.3.3)

表6 屋面桁架结构不确定性参数(例3.3)Table 6 Uncertain parameters of roof truss model (E.3.3)

采用极限状态函数式(25)，基于PDEM-COM方法得到可靠度分析结果如图11所示。注意到，在初始时，由混凝土弹性模量数据进行Bootstrap分析得到的95%置信区间(见图10)范围很窄，这说明该物理参数的认知不确定性程度较低。因此，从图11可见结构可靠指标的变化范围亦较小。

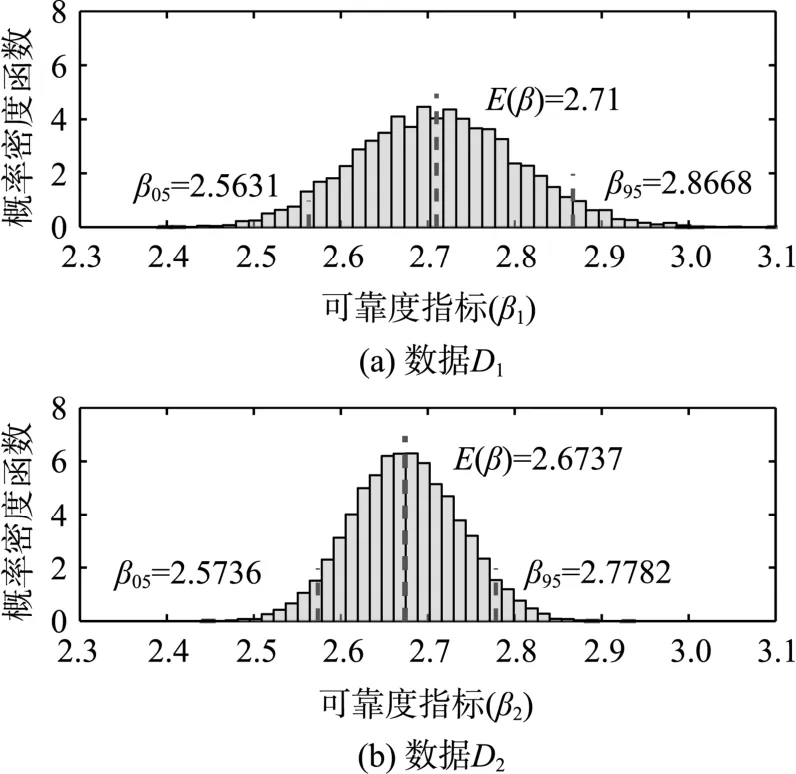
图11 屋面桁架结构可靠度分布Fig.11 Reliability index distributions of roof truss structure via

4 结论

针对数据稀缺与信息更新导致的认知不确定性，引入Bootstrap方法和Bayes更新的方法进行表征。进而，针对固有不确定性与认知不确定性耦合问题，结合概率密度演化理论与概率测度变换(PDEM-COM)，提出了从数据出发到系统中的不确定性量化、传播与可靠性分析的基本途径和数值算法，实现了考虑认知不确定性的工程可靠性高效分析。通过3个工程实例分析，验证了所提方法的有效性。主要结论如下：

(1) 采用Bootstrap方法和Bayes更新方法进行数据稀缺与信息更新时的认知不确定性表征，可方便地结合概率密度演化-测度变换，形成从数据出发到系统不确定性量化的有效途径；

(2) 由于认知不确定性的存在，结构可靠度不再是一个确定值，而是一个随机变量，其置信区间与认知不确定性的程度密切相关；

(3) 基于PDEM-COM的不确定性传播方法具有较高的精度和效率，可适用于工程实际问题分析。

对于认知不确定性导致分布信息发生大偏差、随机输入下复杂工程系统整体动力可靠度及其不确定性量化等问题，尚需今后进一步深入研究。