二维自由振动问题的自适应有限元分析初探

袁 驷，孙浩涵

(清华大学土木工程系，土木工程安全与耐久教育部重点实验室，北京 100084)

自振频率和振型反映了结构动力特性，是抗震分析和结构设计的重要基础，根据已有结构的振型信息判断其受损分布也是当前损伤识别研究的热点[1]。二维自由振动在数学上归结为偏微分方程特征值问题，精确求解缺乏可行性，因而集中质量法、能量法和有限元法(FEM)等一系列离散和近似方法得到了充分发展。凭借处理复杂结构的灵活性和通用性，各类有限元法逐渐成为求解的主要手段[2]。

自适应有限元法(AFEM)是提升求解质量和效率的一种有效方法[3―4]，主要思路是反复在前一次网格的求解信息基础上，利用可靠的误差估计手段对有限元解精度做出估计，并结合有效的网格细化技术调整网格，以获得优化的网格，直至满足用户事先给定的误差限。

单元能量投影(Element Energy Projection，简称EEP)法是袁驷等[5―6]基于数学理论和力学概念，提出的新型有限元超收敛后处理算法，基于其超收敛的优良特性，一整套有限元自适应分析方法已得到充分的发展和应用。该算法基于位移超收敛解估计误差，指导网格细分，可给出按最大模度量的、逐点满足给定误差限的解答，在二维[7―9]及三维[10]线性问题中取得一系列成功，并已成功推广至部分非线性问题[11―12]。

基于EEP法的一维FEM和二维FEMOL特征值问题自适应分析已经取得成功[13―14]。本文方法基于类似的线性化思想，合理引入二维线性问题的EEP自适应分析技术，提出了二维自由振动问题的自适应有限元求解策略。文末若干算例表明，本法可靠，冗余度小，效果颇佳。

1 基本模型及有限元求解

本文以弹性薄膜为模型问题，进行相应的公式推导及算法说明。不失一般性，该算法流程可推广至更加复杂的线弹性体自由振动及失稳分析。

1.1 弹性薄膜自由振动问题

弹性薄膜自由振动在数学上对应于二维Laplace特征值问题，其控制方程可以表示为：

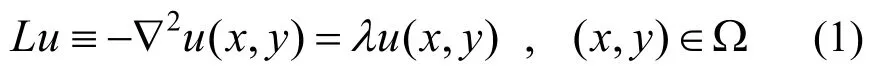
式中：L为线性微分算子；▽2为Laplace算子；λ=ω2ρ/T，ω为自振频率，ρ为薄膜密度，T为薄膜张力；u为对应的振型函数。为方便讨论，沿用数学表达，下文也将λ称为特征值，u称为特征函数，将二者合称为特征对。此外，还应满足适当给定的边界条件。

1.2 二维有限元离散

本文采用双m次四边形单元，单元试探函数uh借助双m次形函数对结点位移插值得到：

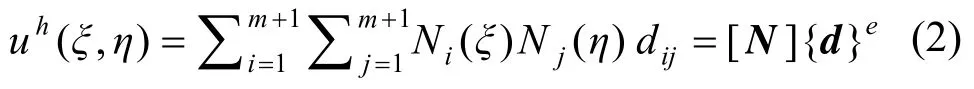
式中：Ni和Nj为m次Lagrange或Hierarchical形函数；dij为相应的结点位移。单元检验函数vh采用相同的形函数插值形式。

由于二维EEP超收敛计算要求，本方案的有限元网格须是“拟线法网格”，即先利用FEMOL的离散方式用一组结线对求解区域进行半离散，然后再沿结线维度进一步离散，得到的网格既是FEMOL常微分方程组(Ordinary Differential Equations，简称ODEs)的广义一维有限元网格，也是原问题的二维有限元网格，如图1所示。

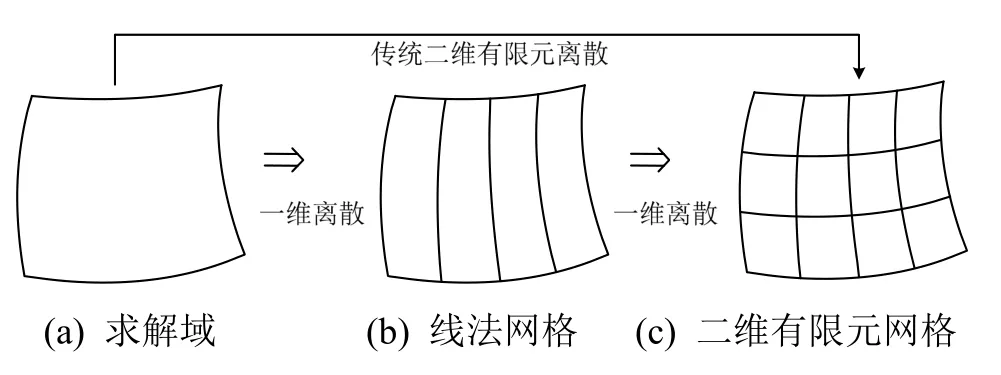
图1 二维问题逐维离散示意图Fig.1 D-by-D discretization of 2D problems

给定网格划分π，标准的FEM过程将建立如下的矩阵广义特征值问题：

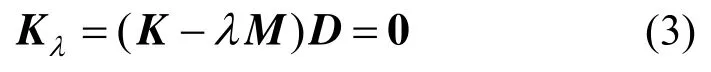
式中：D为振型向量；K和M分别为传统FEM中的整体静力刚度矩阵和一致质量矩阵，二者均与λ无关。

1.3 矩阵广义特征值问题求解

经由1.2节的有限元过程，在当前网格π下，原问题1近似转化为式(3)所示的矩阵广义特征值问题。在本文算法中，采用基于Sturm序列的计数法及逆幂(子空间)迭代进行求解。

对于式(3)，设任给一试探值λa并作特征值移位，则可写作如下形式：

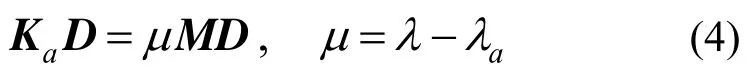
式中，Ka=Kλ(λa)。根据Sturm序列的性质，低于λa的特征值总数可通过J计数公式求得，即：

式中，s{Ka}代表对Ka符号的计数，即以Gauss消元法将Ka消成上三角阵后主对角线上负元素的个数。

以J计数为基础，可通过二分法确定待求阶特征值的区间范围(λl,λu)，从而获得较好的移位值λa∈(λl,λu)(一般可取为λa=(λl+λu)/2)，而后对问题3进行特征值移位后的逆幂(子空间)迭代(即对式(4)进行求解)，并不断更新上、下界(λl,λu)，既保证了特征值的精度，也大幅提高了收敛速度。

2 误差估计及自适应求解

2.1 自适应求解目标

设要求解前n阶特征对(λk,uk) (k=1,2,…,n)，用户给定特征值及特征函数的误差限均为tol。本文算法的最终目标是：在精确解(λk,uk)(k=1,2,…,n)未知的情况下，得到充分好的FEM网格πk，使得该网格下的FEM解(k=1,2,…,n)同时满足。

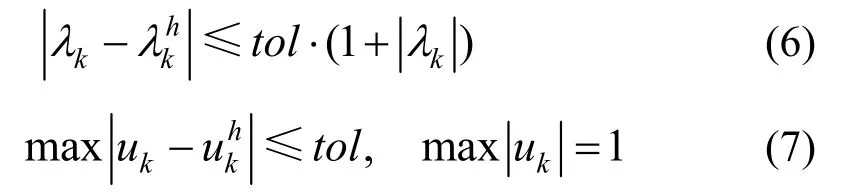
在实际计算时，由于精确解λk、uk未知，上述目标不能作为停机准则，因而采用以下误差控制准则：

2.2 误差估计及自适应网格划分

二维有限元误差估计是本文算法的核心，主要思想是通过等价线性问题[11]，将二维线性有限元EEP超收敛计算方法引入非线性的特征值问题求解中。与传统的基于超收敛分片恢复SPR等方法的误差估计[15―17]不同，在获取超收敛的位移场后，我们采用最大模而非能量模进行误差控制，从而直接控制特征函数求解的误差，十分自然合理。为简化表示，此处以(λh,uh)表示第k阶特征对在当前FEM网格下的解。此时若将式(1)的右端项λu代换为λhuh，则其转化为如下线性问题：

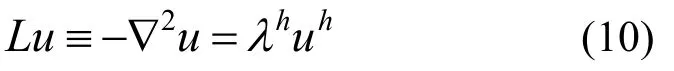
由于逆幂(子空间)迭代已经收敛，若无网格调整，式(10)的FEM解仍为(λhuh)。又由于此时原非线性问题已转化为式(10)的线性问题，从而可引入二维线性EEP超收敛求解公式进行后处理计算，获得合理的误差估计。

限于篇幅，这里不讨论二维线性有限元EEP超收敛公式的具体推导过程，仅简单介绍思路。与“逐维离散”方式相呼应，二维EEP法超收敛计算采用的是“逐维修复”方案。如图2所示，借助有限元线法作为桥梁，分两步利用单元能量投影定理导出单元上任一点的超收敛计算公式。其主要过程为：

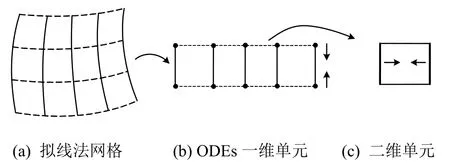
图2 二维问题逐维恢复示意图Fig.2 D-by-D recovery of 2D problems

1) 二维有限元解：在当前网格πk下，经由第1节所述的有限元过程获得第k阶的有限元解(λh,uh)。

2) 拟线法解：采用式(11)对线法常微分方程组的广义一维有限元解进行超收敛计算得到“拟线法解”，用之代替线法解，其计算公式为：

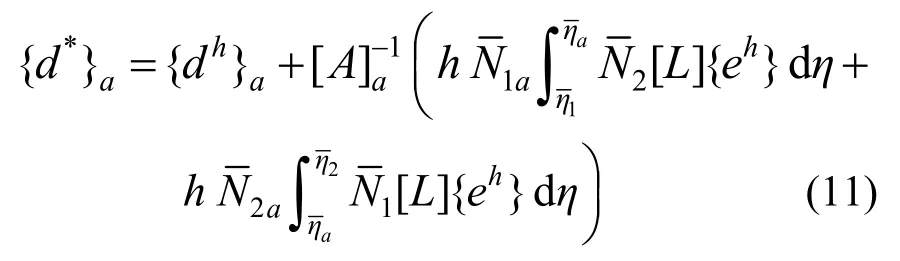
3) 全域超收敛解：将问题视为有限元线法的超收敛计算，再次利用单元能量投影定理，通过式(12)获得全域的二维有限元超收敛解，其计算公式为：

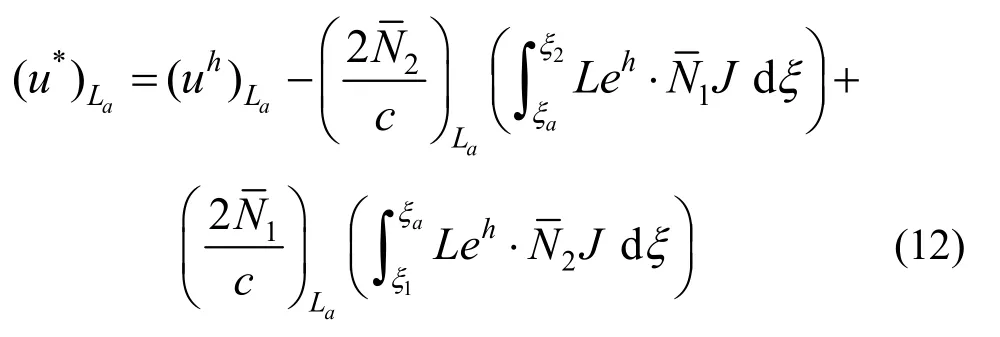
式(11)和式(12)中各参数的含义及计算请详见文献[7―8]，在此不再赘述。通过以上过程获得EEP超收敛解后，即可定义单元上任意一点的估计误差：

在本文中，基于该误差估计，采用均差法[9]进行网格细分，其高效稳健特性已被大量数值算例验证。该法生成的网格分布合理、误差冗余度小。

2.3 自适应求解步骤

与基于FEMOL的特征值问题自适应求解类似[13]，对每阶待求的特征对，基于以上分析本文算法可归结为：

1) 划界阶段：在当前二维FEM网格上(首阶网格π0人为给定，第k+1阶初始网格取为第k阶最终网格)，基于J计数采用二分法得到待求特征值的上、下界。

2) 定解阶段：采用移位的逆幂(子空间)迭代法得到该网格上特征对的有限元解，利用二维有限元的EEP超收敛公式计算超收敛解，检验误差并进行必要的网格细分；在获得的新网格上重复该迭代过程，不断更新待求特征值的上、下界及相应特征函数，直至满足误差要求。

该算法高效、精确、通用、可靠，实现了精确的频率和振型求解。相对于课题组之前提出的特征值问题FEMOL自适应分析算法，本文算法在二维的两个方向进行离散，进一步降低了冗余度，提高了求解效率，增强了灵活性。

3 数值算例

本文算法已编制成Fortran90程序。若无特殊说明，下文算例均采用三次元进行计算，误差限给定为tol=10-3。为保证超收敛计算的准确性，在进行逆幂(子空间)迭代时，收敛指标设置为更加苛刻的10-8，即当前后两次迭代符合

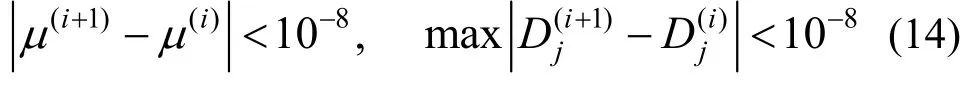
认为该次逆幂(子空间)迭代已经收敛。下文中，第k阶最终特征值取为估计上、下界的中值，即误差比较采取特征值混合误差

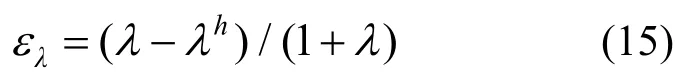
和振型绝对最大误差

并相应定义特征值误差比ελ/tol及振型误差比εu/tol，误差比小于1即表明自适应求解圆满完成。下面通过若干典型的弹性薄膜自由振动算例表明算法的有效性。

例1.固支方膜

考虑图3所示的四边固支方膜的自由振动问题，其精确解如下：

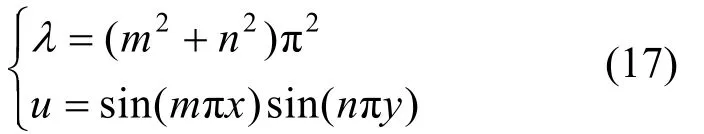
其中，m(m=1,2,3,…)及n(n=1,2,3,…)分别表示在x及y方向的半波数目，当二者交换取值时将出现重频。采用本文方法求解前10阶特征对，并将结果汇总至表1。

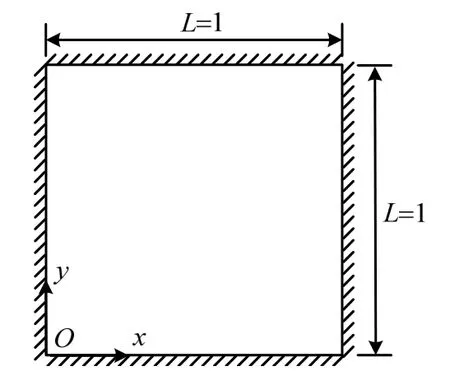
图3 固支方膜计算简图Fig.3 Clamped square membrane model

表1 固支方膜自由振动求解结果Table 1 Results for clamped square membrane vibration

从表1结果可以看到，该算法能够很好地进行误差控制，各阶特征对求解均满足误差要求，且从振型误差比可以看到，本方法冗余度小。重频情况可以有无穷多种振型组合，因此其振型误差比不在此列出。

图4为固支方膜的第1阶振型图，图5和图6分别为最终网格下的第1阶振型真实误差分布及估计误差分布，可以看到，针对有限元解进行的EEP后处理过程在全域给出了相当准确的误差估计，从而可以有效地指导网格划分。本文方法对于重频求解依然有效，以第5阶及第6阶的重频为例，得到的振型分别如图7、图8所示，对应于m=1,n=3及m=3,n=1的情况。

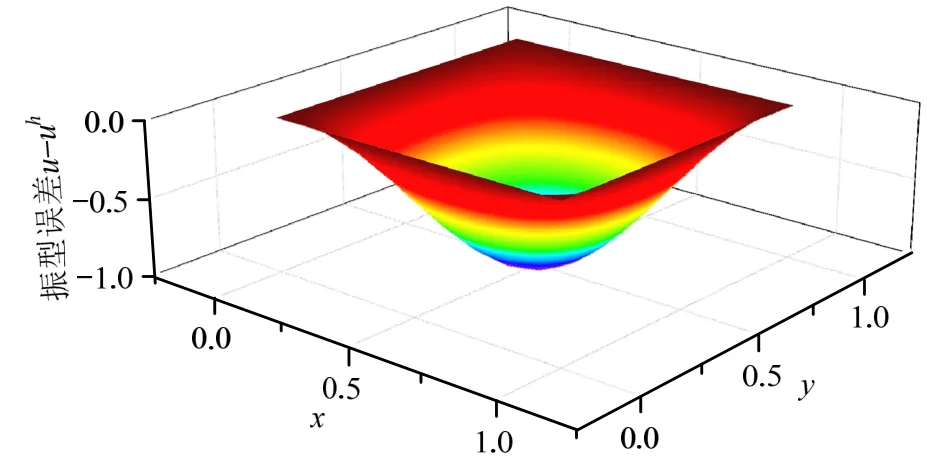
图4 固支方膜第1阶FEM解振型图Fig.4 1st order vibration mode of clamped square membrane by FEM

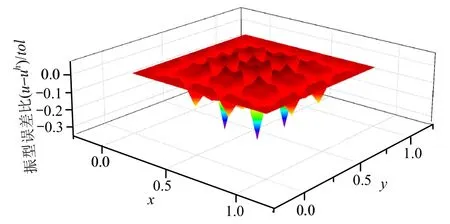
图5 固支方膜第1阶振型域内误差分布Fig.5 Error distribution of 1st order vibration mode of clamped square membrane

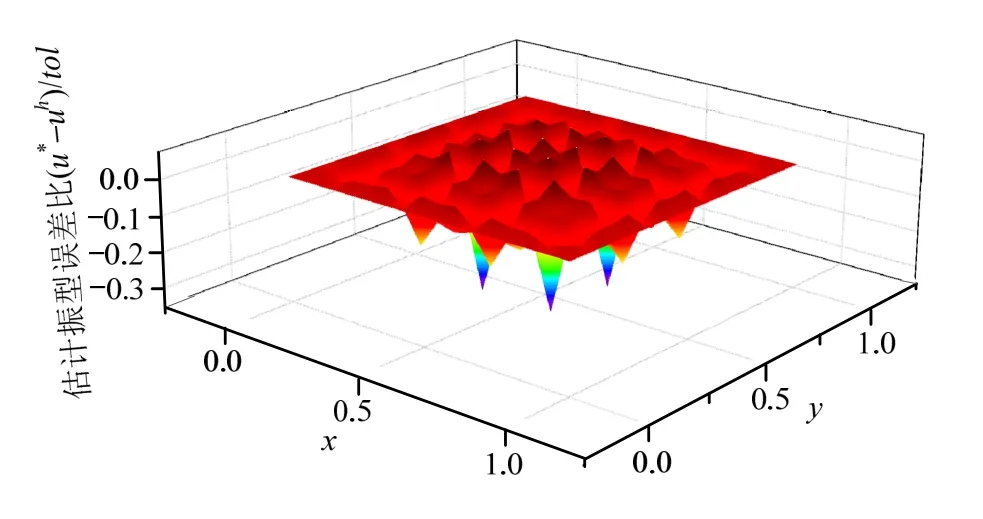
图6 固支方膜第1阶振型域内估计误差分布Fig.6 Error estimation of 1st order vibration mode of clamped square membrane

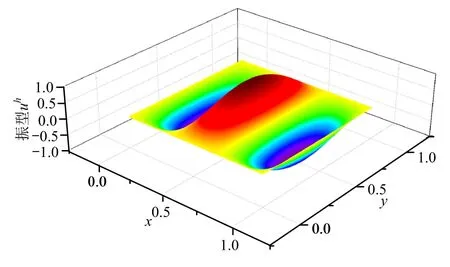
图7 固支方膜第5阶FEM解振型图Fig.7 5th order vibration mode of clamped square membrane by FEM

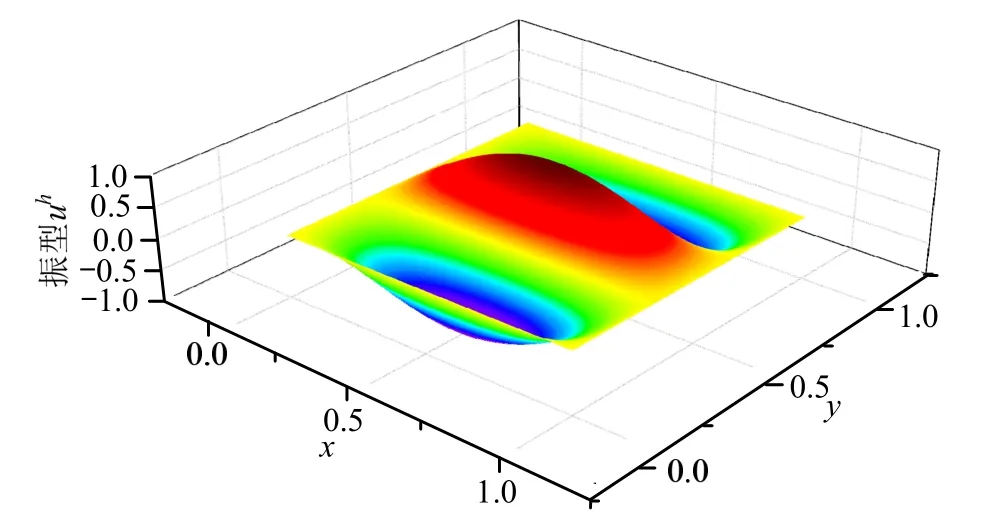
图8 固支方膜第6阶FEM解振型图Fig.8 6th order vibration mode of clamped square membrane by FEM

例2.固支L形膜

考虑L形固支薄膜自由振动问题。计算简图如图9所示，初始网格采用2个四边形单元。该例中求解域的凹角造成了一定的奇异性，从而增大了求解的难度。作为经典的具有奇异性的问题，已有很多学者对该问题进行过研究，文献[18]给出了其较为准确的频率上、下界估计。

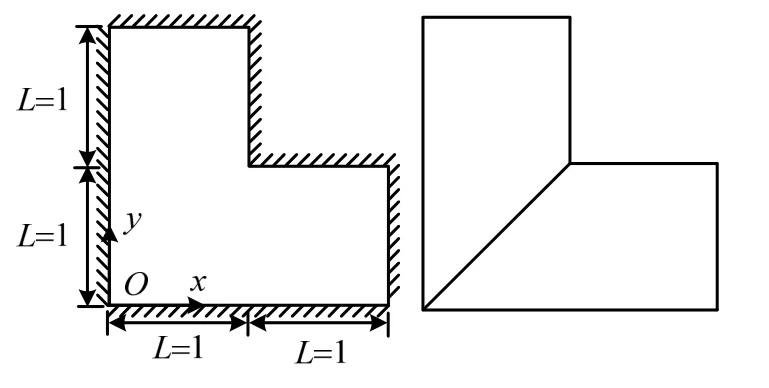
图9 固支L形膜计算简图(左)及初始网格(右)Fig.9 Clamped L-shape membrane model (left) and initial mesh (right)

图10为首阶特征对自适应求解的最终网格。不同于文献[13]中采用特殊的射线网格以适应问题的奇异性，我们看到随着自适应过程的进行，网格自动地向奇异点附近加密以适应问题性质。图11和图12给出了具有典型性的第1阶及第5阶振型图。表2给出了该问题前10阶求解结果，均严格满足求解目标。

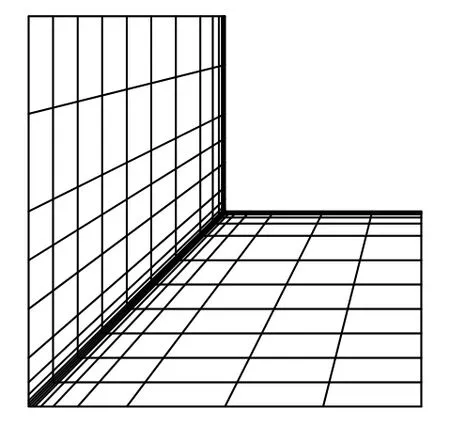
图10 固支L形膜第1阶特征对自适应求解最终网格Fig.10 Final mesh of adaptive procedure for 1st order eigenpair of clamped L-shaped membrane

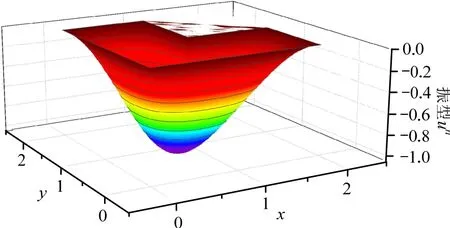
图11 固支L形膜第1阶FEM解振型图Fig.11 1st order vibration mode of clamped L-shaped membrane by FEM

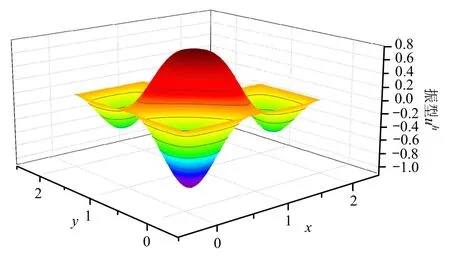
图12 固支L形膜第5阶FEM解振型图Fig.12 5th order vibration mode of clamped L-shaped membrane by FEM

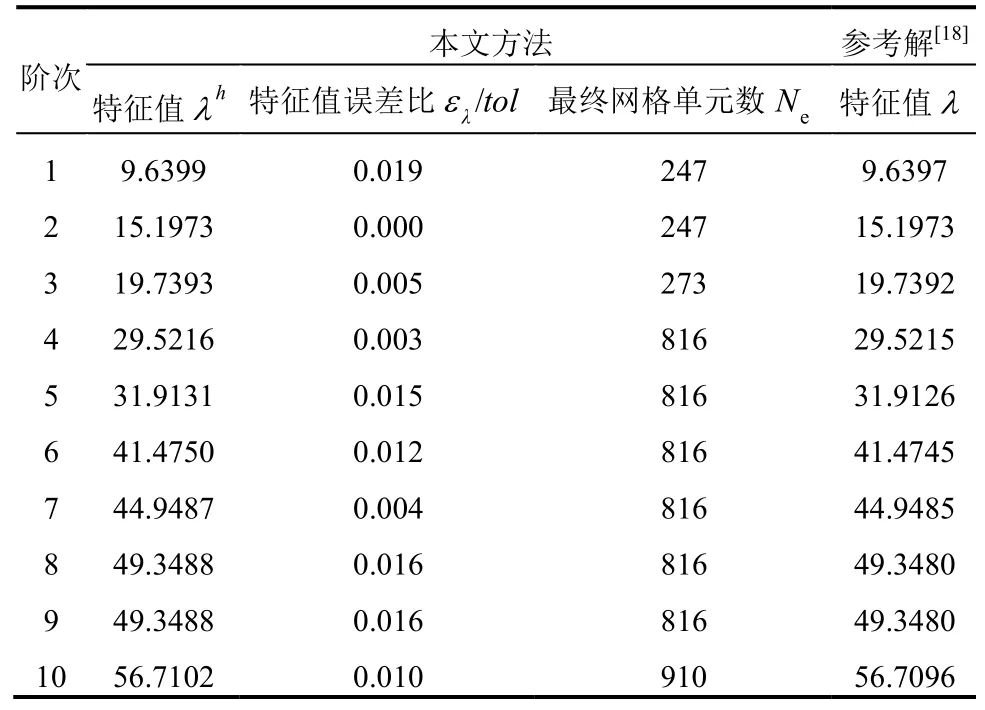
表2 固支L形膜自由振动求解结果Table 2 Results for clamped L-shaped membrane vibration

例3.带裂缝方膜

考虑具有奇异性的带裂缝方膜问题，其计算模型及初始网格如图13所示。根据对称性，取半结构进行计算，只计算对称情况的自由振动。该问题可定义为：

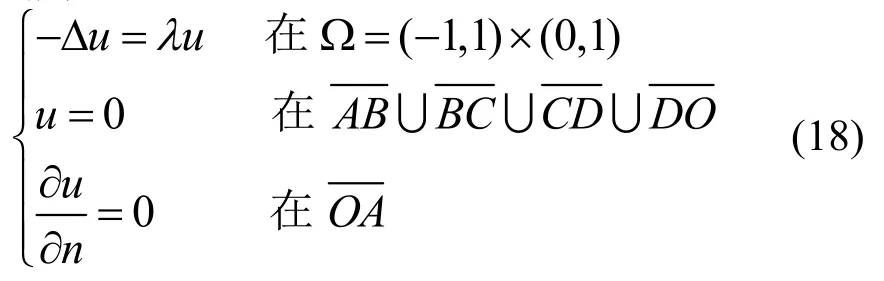
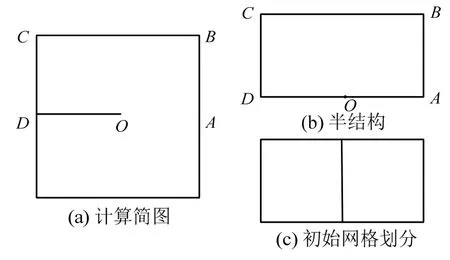
图13 带裂缝方膜Fig.13 Square membrane with an inside crack

在文献[19]中，作者采用Trefftz方法对Laplace算子的特征值问题进行求解，并对该带裂缝方膜问题给出了前两阶数值精确的特征值，可用来检验本文算法的可靠性。图14为自适应求解第1阶特征对的最终网格，可以看到无须人为干涉，自适应过程便自动识别了该问题在O点的强奇异性。

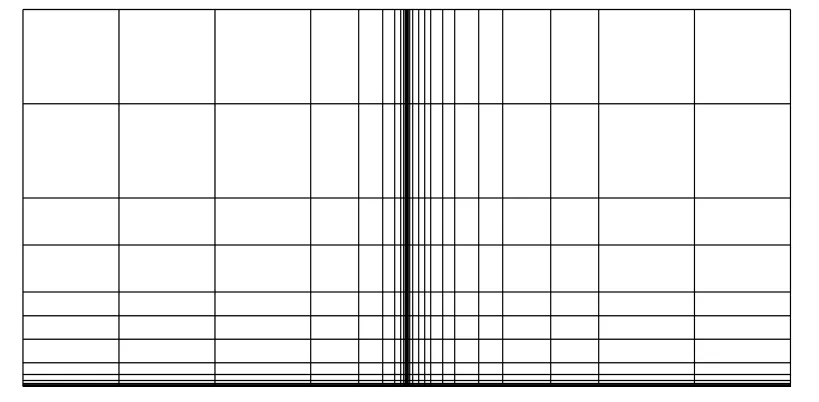
图14 带裂缝方膜第1阶特征对自适应求解最终网格Fig.14 Final mesh of adaptive procedure for 1st order eigenpair of crack membrane

图15和图16分别为第1阶和第3阶振型图。表3列举了前5阶的求解结果，与文献中前2阶的结果相比较，本算法获得了令人满意的效果。

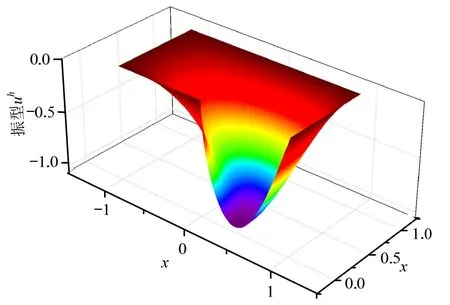
图15 带裂缝方膜第1阶FEM解振型图Fig.15 1st order vibration mode of crack membrane by FEM

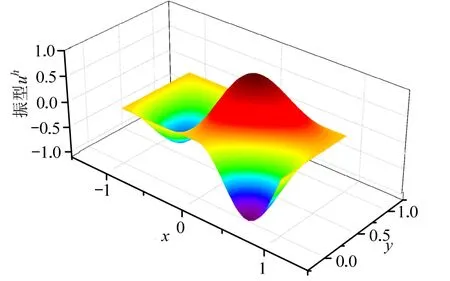
图16 带裂缝方膜第3阶FEM解振型图Fig.16 3rd order vibration mode of crack membrane by FEM

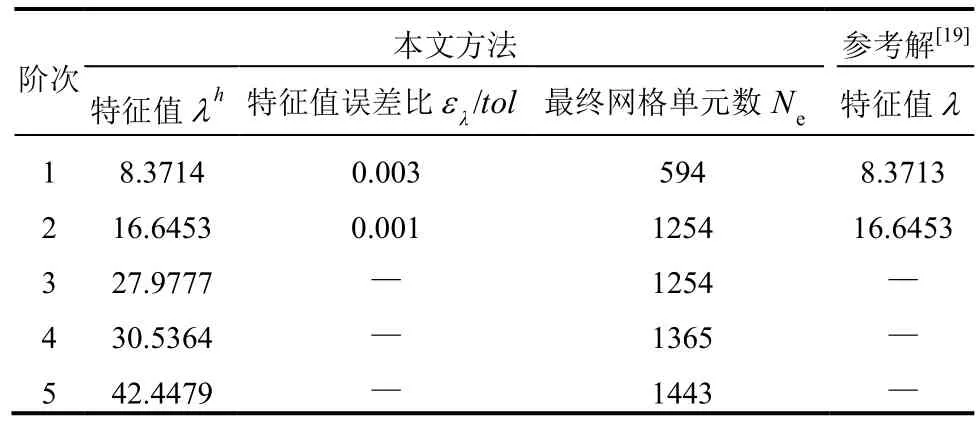
表3 带裂缝方膜自由振动求解结果Table 3 Results for crack membrane vibration

例4.固支圆膜

考虑定义在半径为1的圆形区域的Laplace特征值问题，计算简图及初始网格如图17所示。其极坐标下解析的特征值及特征函数[20]为：

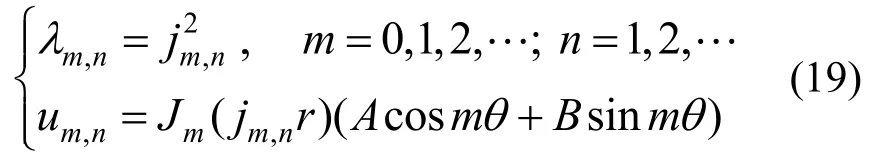
式中：Jm为第一类m阶Bessel函数；jm,n为其第n阶根，即：

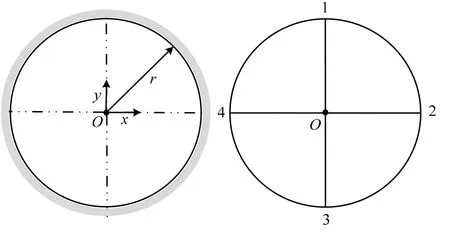
图17 固支圆膜计算简图(左)及初始网格(右)Fig.17 Clamped circular membrane model (left) and initial mesh (right)

对于该圆膜自由振动问题，文献[21]也通过理论分析和数值方法给出了自振频率。我们采用四次精确几何单元进行计算，将前10阶的计算结果汇总至表4。由于圆膜的对称性，在有限元求解过程中我们发现对于其中若干阶次，将求得重频率的情况。但遵循文献[20―21]的表示，表4中不再对其单独列举。由于该问题并不具有奇异性，从图18所示的自适应最终网格我们也可以看到其性质相对均匀，再次说明基于EEP误差估计的网格划分具有良好的合理性。图19～图22分别为有限元求得的固支圆膜第3阶、4阶、5阶、7阶振型。

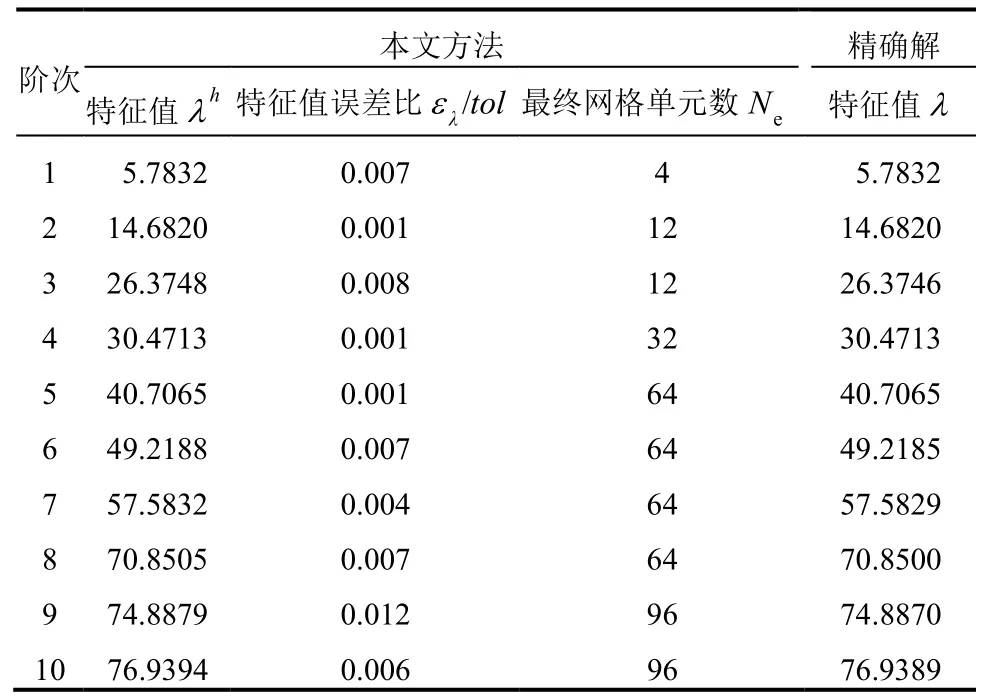
表4 固支圆膜自由振动求解结果Table 4 Results for clamped circular membrane vibration

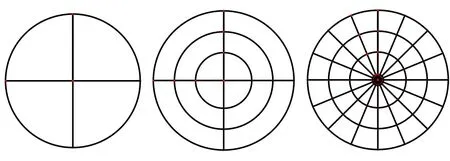
图18 固支圆膜第1阶、3阶、5阶自适应最终网格Fig.18 Final mesh of 1st, 3rd and 5th order with adaptive procedure for the clamped circular membrane

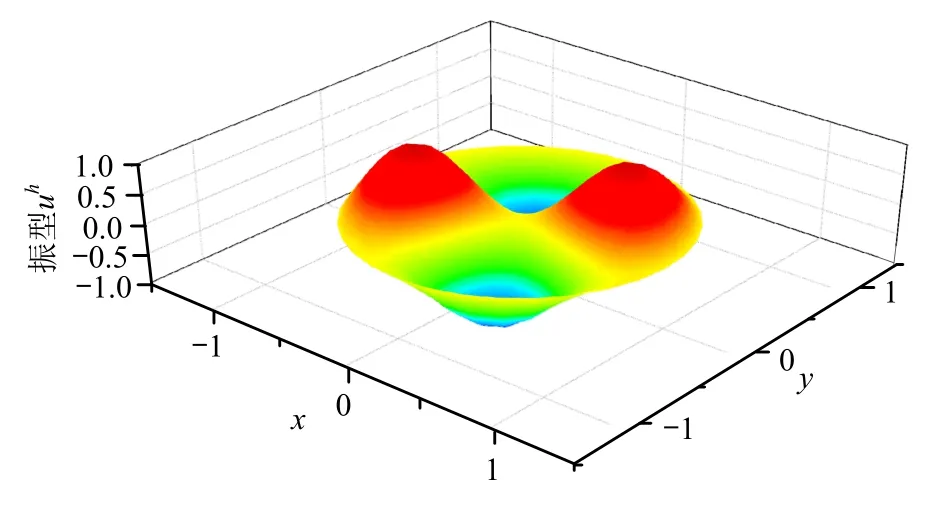
图19 固支圆膜第3阶FEM解振型图Fig.19 3rd order vibration mode of clamped circular membrane by FEM

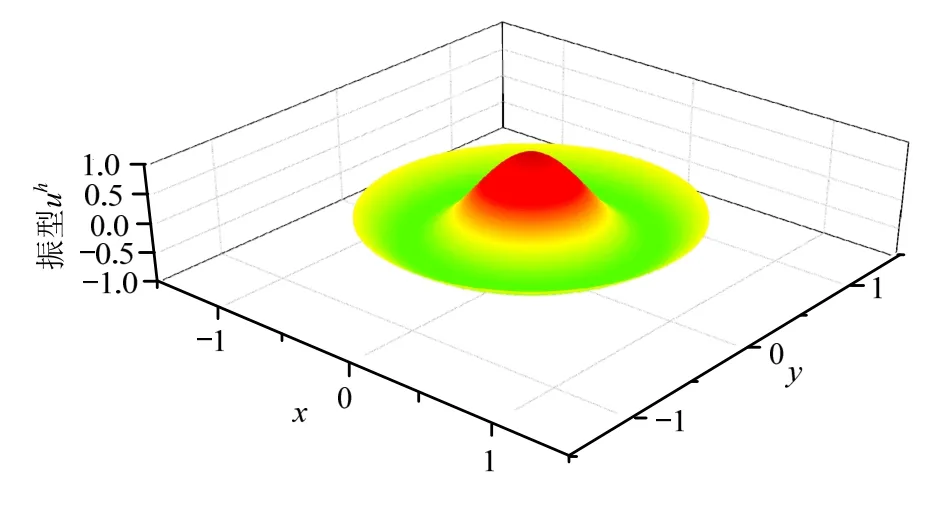
图20 固支圆膜第4阶FEM解振型图Fig.20 4th order vibration mode of clamped circular membrane by FEM

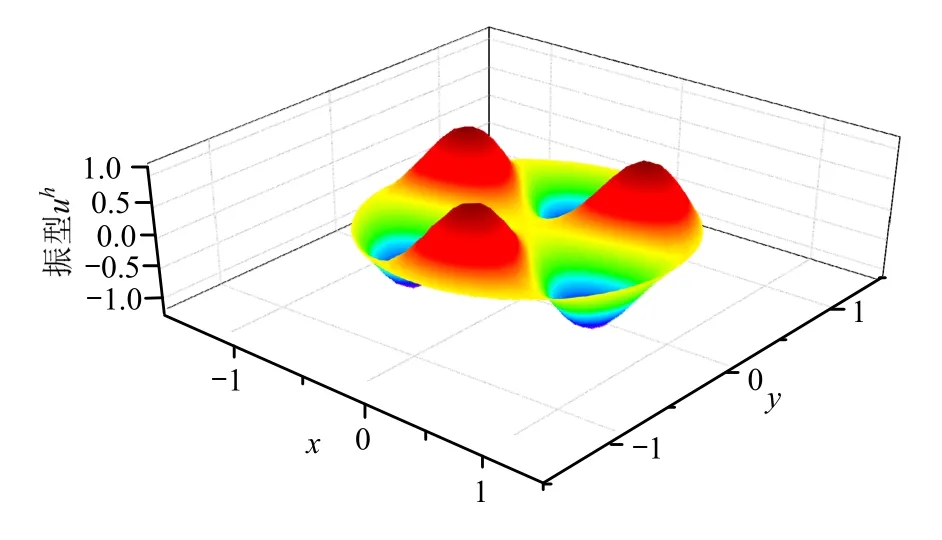
图21 固支圆膜第5阶FEM解振型图Fig.21 5th order vibration mode of clamped circular membrane by FEM

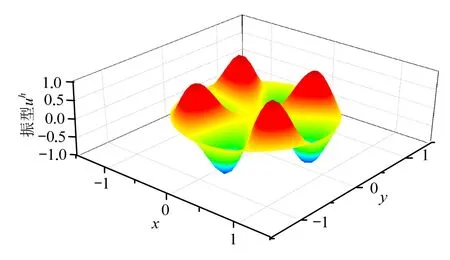
图22 固支圆膜第7阶FEM解振型图Fig.22 7th order vibration mode of clamped circular membrane by FEM

图23及图24分别给出了第4阶振型自适应最终网格下的实际误差及估计误差，全域上逐点误差比均满足要求，且估计误差分布与实际误差分布接近。

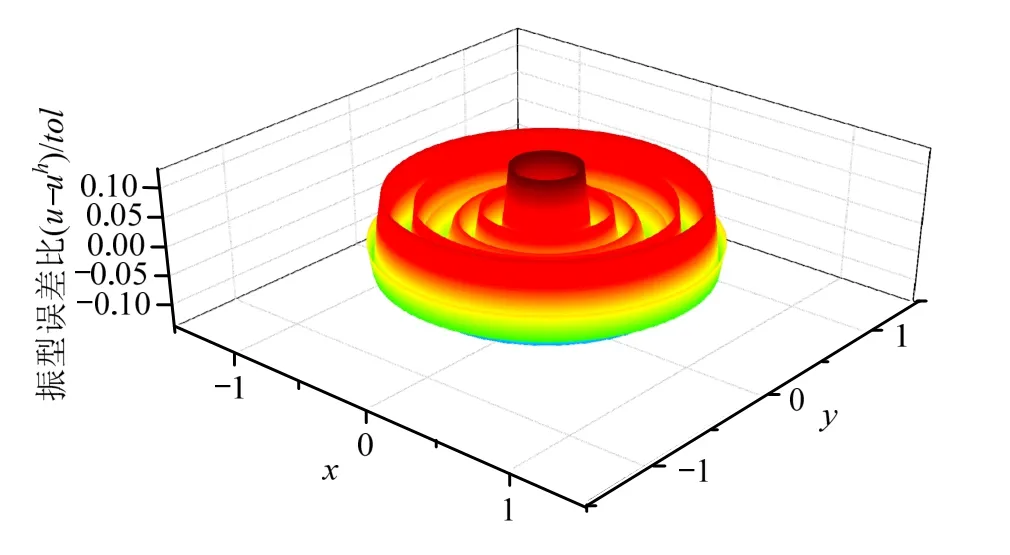
图23 固支圆膜第4阶振型域内误差分布Fig.23 Error distribution of 4th order vibration mode of clamped circular membrane

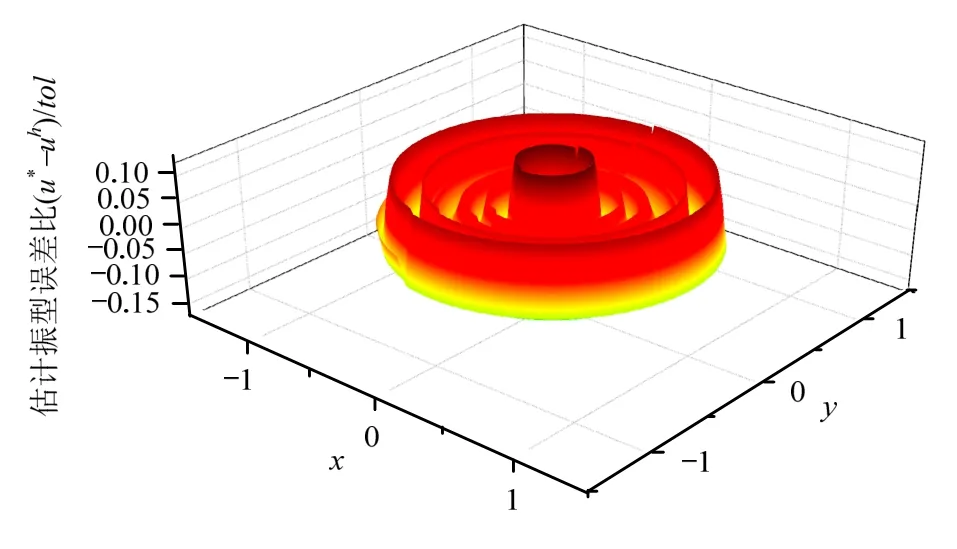
图24 固支圆膜第4阶振型域内估计误差分布Fig.24 Error estimation of 4th order vibration mode of clamped circular membrane

4 结论

本文提出的基于EEP法的二维自由振动问题有限元自适应分析方法，通过合理的线性化步骤，将业已成熟的二维线性有限元EEP后处理技术引入，思路清晰，结果可靠，可得到满足精度要求的自振频率和按最大模度量满足用户给定误差限的振型，展示出稳定的优良特性。本文算法可拓展性强，未来结合本课题组在网格局部加密方面的最新研究成果[22]，有望进一步提高求解效率。