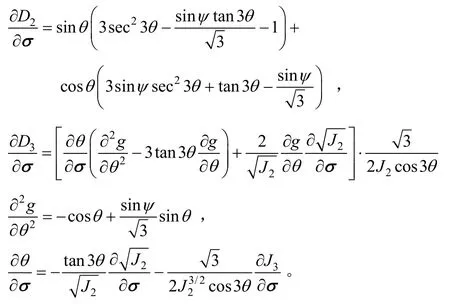基于Hoek-Brown准则的应变软化模型有限元数值实现研究

金俊超，佘成学，尚朋阳

(武汉大学水资源与水电工程科学国家重点实验室，湖北，武汉 430072)

自1980年Hoek-Brown(H-B)准则被首次提出以来，由于其具备综合考虑了岩块和结构面的强度以及岩体结构等多种因素的影响，能够反映岩体的非线性破坏特征，较好地解决了Mohr-Coulomb(M-C)、Drucker-Prager(D-P)强度准则受拉破坏处理上的困难，并已建立了一套比较完善的参数确定方法等特点，在岩体工程中得到了广泛使用[1−5]。

然而，当前仅有少量有限元软件中集成了H-B准则本构模型，这限制了H-B准则在数值计算中的应用。虽然也有学者[6−12]通过二次开发等方法，将H-B准则理想弹塑性模型嵌入ABAQUS、GeoFBA3D等有限元软件中，但上述研究并未实现H-B准则应变软化问题的求解。尽管文献[13]采用显示差分算法，实现了H-B准则应变软化求解，但该方法并不适用于有限元计算。而虽然文献[14]给出了考虑应变软化的H-B准则本构积分，但文中对于具体的有限元软化求解过程未给出明确说明，考虑到经典塑性力学对于软化速率是有限制的[15]，该方法可能无法求解峰后软化速率较大的情况。因此，有必要进一步研究基于H-B准则的应变软化模型有限元数值实现方法。

关于应变软化问题有限元求解，文献[16-17]指出可将应变软化过程转化为一系列的应力脆性跌落与塑性流动过程，软化求解问题就转化为一系列脆塑性求解问题，有效避免了经典塑性力学对于软化速率的限制[15]，并提出了基于最小主应力不变跌落的M-C准则应变软化模型有限元实现方法。 但是上述研究主要存在下述两点不足有待解决：1) 采用的脆塑性计算方法的合理性有待分析，最小主应力不变跌落能否正确描述岩石的变形破坏，是否应引入其他脆塑性计算方法来进行软化求解，还需要针对不同类型破坏现象，进行分析论证；2) 未解决H-B准则应变软化模型的有限元求解问题。

鉴于上述存在的不足，本文首先分析当前不同脆塑性计算方法的合理性，确定合理的脆塑性计算方法。在此基础上，推导给出H-B准则脆塑性及理想弹塑性的隐式本构积分算法，并采用一系列脆性跌落-塑性流动，将H-B准则应变软化模型嵌入有限元软件ABAQUS中。然后，通过与应变软化圆隧围岩的力学响应规律的解析解对比，检验所建模型的正确性。最后，将模型应用于某薄上覆盖岩层高内水压输水隧洞工程，分析运行期围岩结构的稳定性。

1 不同脆塑性计算方法合理性分析

针对脆塑性求解问题，国内外诸多学者进行了研究，根据假设不同，有以下3种脆塑性计算方法：偏应力等比例跌落[18-19]、最小主应力不变跌落[16-17]及塑性位势跌落[15,20]。

岩石的变形破坏可分为单轴拉伸破坏、拉剪破坏、纯剪破坏及压剪破坏，见图1。基于M-C准则及H-B准则，分析上述3种方法对单轴拉伸破坏、单轴压缩破坏及二向纯剪破坏计算是否正确，若单轴压缩破坏、单轴拉伸破坏及二向纯剪破坏可正确计算，则拉剪、压剪等复合破坏类型也可正确计算。

图1 基于M-C准则和H-B准则的岩石破坏分类Fig.1 Rock failure types based on the M-C criterion and the H-B criterion

1.1 偏应力等比例跌落不合理性论证

偏应力等比例跌落假设应力由峰值屈服面径向跌落至残余屈服面上，有且仅有各向应力偏量按同一比例β衰减[18-19]。若设峰值强度面应力张量为σp，则残余强度面应力张量为σr为：

1) 单轴拉伸破坏不可行论证

当岩石单轴拉伸破坏时，峰值强度面应力张量σp为(应力以拉为正)：

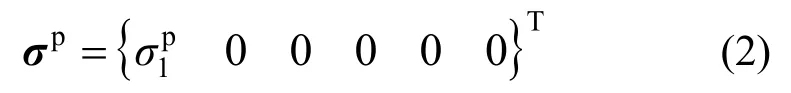
联立式(1)和式(2)，可得到残余强度面应力张量σr为：

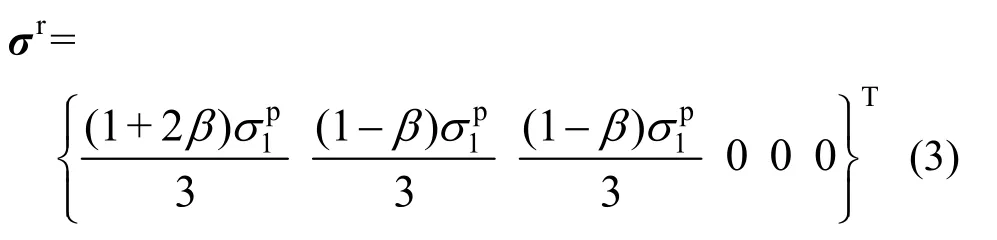
将σp和σr代入屈服函数，得到：

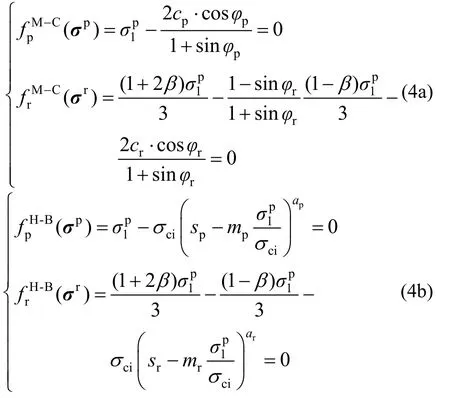
式中：上标M-C表示M-C准则屈服函数；上标H-B表示H-B准则屈服函数；下标p表示峰值强度面；下标r表示残余强度面。

求解式(4a)和式(4b)可以发现，不管是采用M-C准则还是H-B准则，残余强度系数β均不为1，即说明当岩石发生单轴拉伸破坏后，残余阶段不满足单轴拉伸的应力状态，与试验结果不符，证明偏应力等比例跌落不能正确计算岩石单轴拉伸破坏。

2) 单轴压缩破坏不可行论证

当岩石单轴压缩破坏时，峰值强度面应力张量σp为：

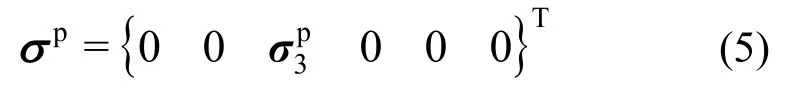
联立式(1)和式(5)，得到残余强度面应力张量σr：

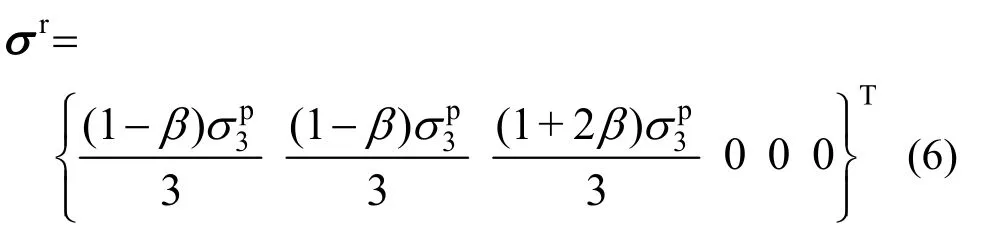
将σp和σr代入屈服函数，得到：

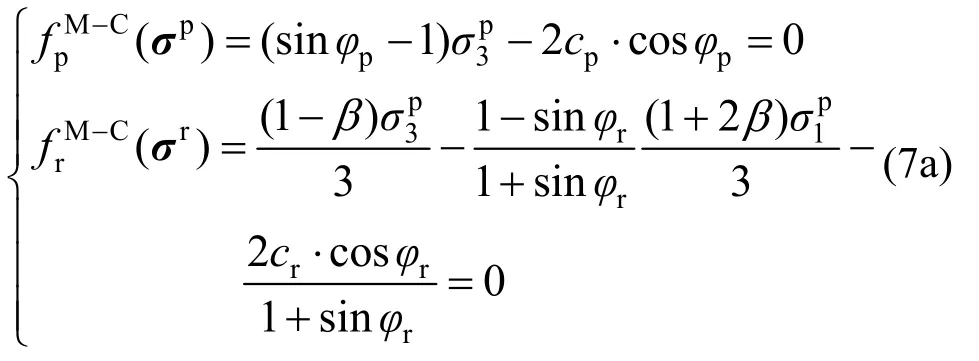
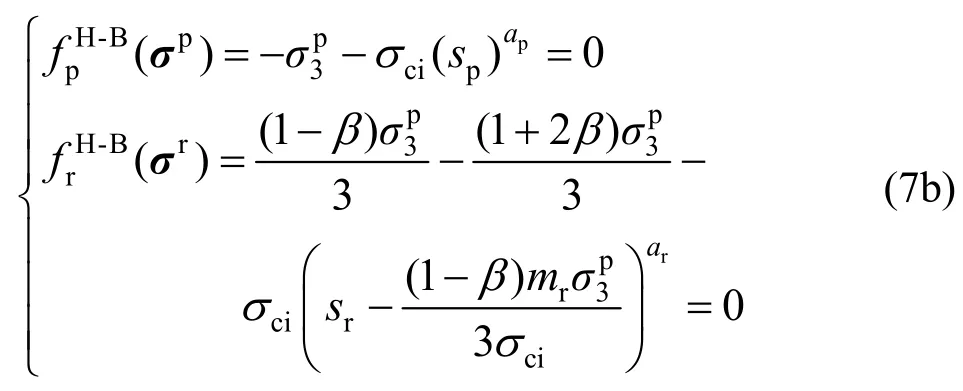
求解式(7a)和式(7b)可以发现，不管是采用M-C准则还是H-B准则，残余强度系数β均不为1，即说明当岩石发生单轴压缩破坏后，其残余阶段不满足单轴压缩的应力状态，与试验结果不符，证明偏应力等比例跌落不能正确计算岩石单轴拉伸破坏。

3) 二向纯剪破坏可行论证

当岩石二向纯剪破坏时，峰值强度面应力张量σp为：

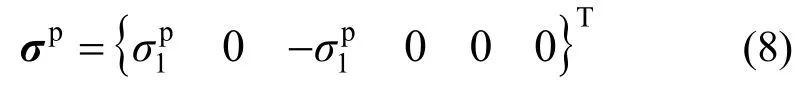
联立式(1)和式(8)，得到残余强度面应力张量σr：

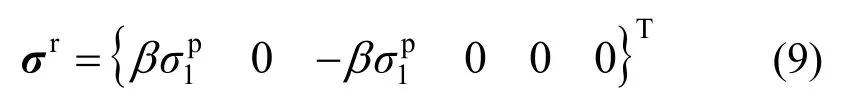
将σp和σr代入屈服函数，将和代入屈服函数，即可求解残余强度系数β，限于篇幅，不再详细展开。不管是采用M-C准则还是H-B准则，残余阶段均满足二向纯剪的应力状态，与试验结果相符，证明偏应力等比例跌落可正确计算岩石二向纯剪破坏过程。

综合上述分析可知，偏应力等比例跌落存在不足，不能正确计算岩石单轴拉伸破坏和单轴压缩破坏，进一步拉剪、压剪等复合破坏类型也可能计算错误。

1.2 最小主应力不变跌落不合理性论证

最小主应力不变跌落针对以压应力为正的情况，假设应力跌落过程中最小主应力不变，应力从峰值强度跌落至残余强度时Lode参数不变[16―17]。对于以拉应力为正的情况，有：

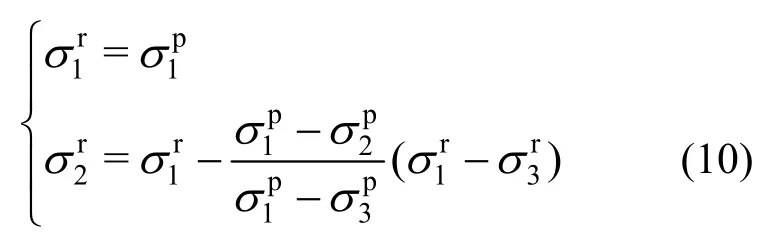
1) 单轴拉伸破坏不可行论证

对于单轴拉伸破坏，其峰值强度面应力张量σp见式(2)，通过联立式(2)和式(10)，得到残余强度面应力张量σr：

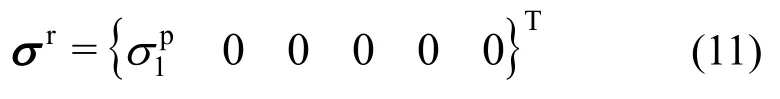
将σp和σr代入屈服函数，得到：

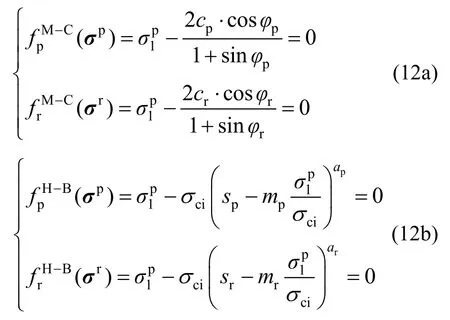
求解式(12a)和式(12b)发现无解，证明最小主应力不变跌落不可正确计算岩石单轴拉伸破坏。

2) 单轴压缩破坏可行论证

对于单轴压缩破坏，其峰值强度面应力张量σp见式(5)，通过联立式(5)和式(10)，得到残余强度面应力张量σr：

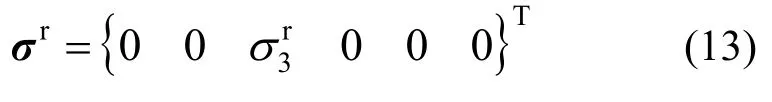
将σp和σr代入屈服函数，即可求得量值，限于篇幅，不再详细展开。不管是采用M-C准则还是H-B准则，残余阶段均满足单轴压缩的应力状态，与试验结果相符，证明最小主应力不变跌落可正确计算岩石单轴压缩破坏。

3) 二向纯剪破坏不可行论证

对于二向纯剪破坏，其峰值强度面应力张量σp见式(8)，通过联立式(8)和式(10)，得到残余强度面应力张量σr：

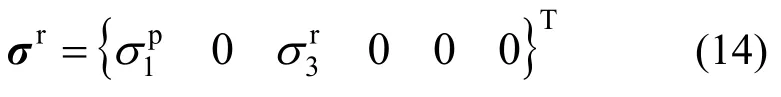
将σp和σr代入屈服函数，得到：

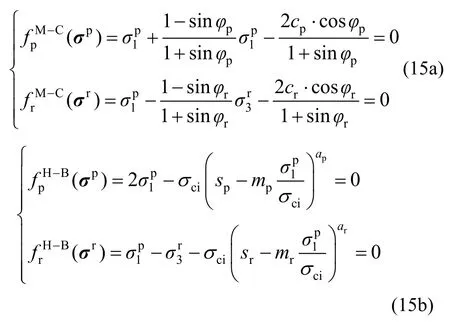
求解式(15a)和式(15b)可以发现，不管是采用M-C准则还是H-B准则，均有说明当岩石发生二向纯剪破坏后，残余阶段不满足二向纯剪的应力状态，明显与试验结果不符，证明最小主应力不变跌落计算不能正确计算岩石二向纯剪破坏。

综合上述分析可知，最小主应力不变跌落存在不足，不能正确计算岩石单轴拉伸破坏及二向纯剪破坏，进一步拉剪、压剪等复合破坏类型也可能计算错误。

1.3 塑性位势跌落合理性论证

塑性位势跌落假设脆性材料仍满足Il’yushin公设，跌落过程产生的塑性应变增量pΔε的方向仍然满足塑性位势理论[15,20]，为：

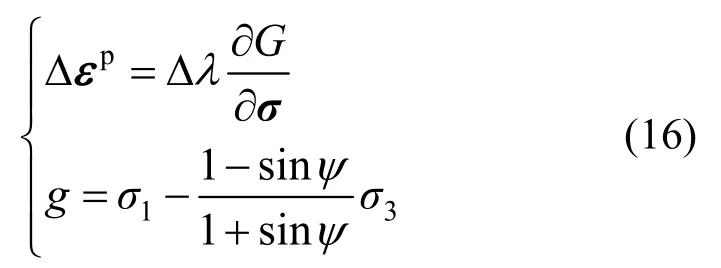
式中，Δλ为塑性乘子，塑性势函数g取M-C准则。

1) 单轴拉伸破坏可行论证

对于单轴拉伸破坏，其峰值强度面应力张量σp见式(2)，由于应力位于π平面张拉棱线上，造成塑性位势求导的数值奇异，为此本文将单轴拉伸破坏问题退化为一维问题进行分析，仅有拉伸方向存在峰值应力此时塑性势函数退化为：

联立式(16)和式(17)可知，只有拉伸方向产生塑性应变对应的残余应力

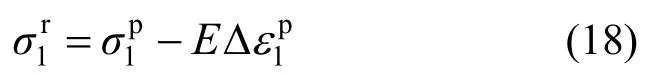
式中，E为弹性模量。

2) 单轴压缩破坏可行论证

对于单轴压缩破坏，其峰值强度面应力张量σp见式(5)，由于应力位于π平面压棱线上，造成塑性位势求导的数值奇异，为此本文将单轴压缩破坏问题退化为一维问题进行分析，仅有压缩方向存在峰值应力此时塑性势函数退化为：

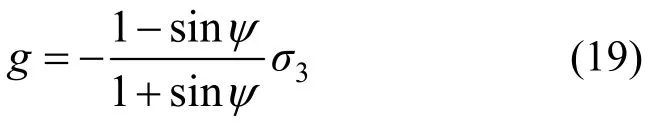
联立式(16)和式(19)可知，只有压缩方向产生塑性应变对应的残余应力

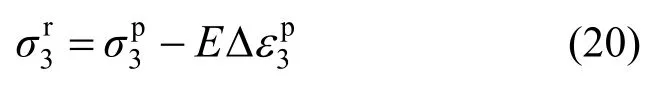
3) 二向纯剪破坏可行论证

对于二向纯剪破坏，其峰值强度面应力张量σp见式(8)。假设岩石纯剪破坏过程不产生塑性体应变，即剪胀角为0°[9-10]，联立式(8)和式(16)可知，只有1方向和3方向产生塑性应变，且：

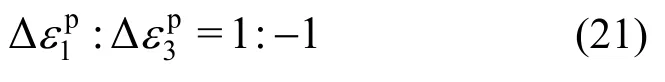
对应的残余强度面应力张量σr：

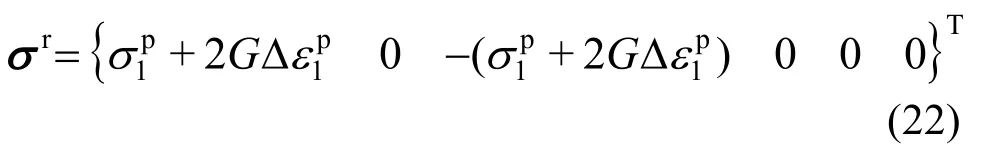
式中，G为剪切模量。

将σp和σr代入屈服函数，即可求得量值，限于篇幅，不再详细展开。不管是采用M-C准则还是H-B准则，残余阶段均满足二向纯剪的应力状态，与事实相符，证明塑性位势跌落可正确计算二向纯剪破坏。

综合上述分析结果可知，塑性位势跌落可正确计算岩石单轴拉伸破坏、单轴压缩破坏及二向纯剪破坏，至于拉剪、压剪等复合破坏类型也可正确计算，而偏应力等比例跌落和最小主应力不变跌落均存在不足。

2 H-B准则应变软化模型有限元数值实现

以拉应力为正，压应力为负，以应力不变量表示的H-B屈服准则为：

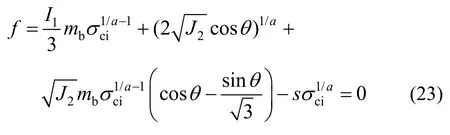
式中：I1为第一应力不变量；J2为第二偏应力不变量；J3为第三偏应力不变量；

通过建立强度参数随塑性参数的演化方程，即可实现应变软化过程的模拟，具体的演化模型研究可参见文献[21-23]。

考虑到通常采用剪胀角来衡量岩体的剪胀变形，以应力不变量表示的M-C准则塑性势函数为：

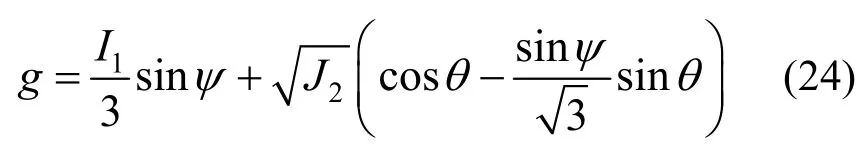
采用一系列脆性跌落-塑性流动，进行H-B应变软化模型的有限元求解，其中数值实现的关键在于H-B脆塑性及理想弹塑性本构积分的实现。

尽管基于D-P、M-C等准则的塑性位势跌落本构积分算法已有相关研究[15,20]，但并未有学者给出基于H-B准则的塑性位势跌落本构积分算法；另外，虽然关于H-B准则理想弹塑性本构积分算法也已有大量研究[6-12]，但其塑性函数通常采用H-B准则，少有采用M-C准则的。为此，2.1节推导给出基于M-C准则塑性势函数的，H-B准则脆塑性及理想弹塑性的隐式积分算法。

2.1 H-B准则脆塑性隐式本构积分算法

假定第n+1增量步开始时应力为σn，应变增量为Δεn，塑性应变为计算弹性试探应力σtr：

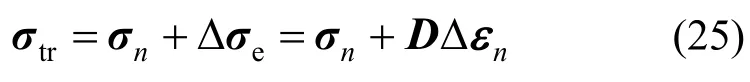
其中，D为弹性刚度矩阵。

若应力在峰值强度屈服面fp内，即则σn+1=σtr；若应力位于或超出峰值强度屈服面fp，即如图2所示，则发生脆塑性应力跌落，到残余强度屈服面，初次回拉应力σC为：

式中：下标B表示对σB的计算结果；由于发生脆塑性应力跌落后，岩石进入理想弹塑性变形阶段，取A=0。

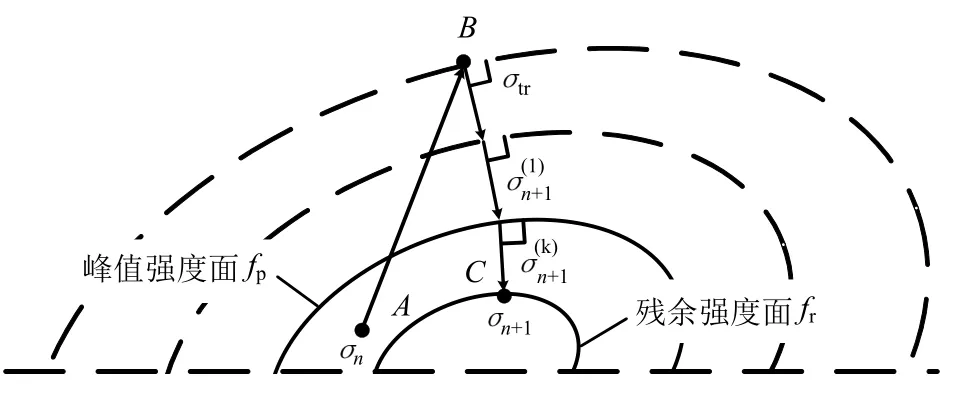
图2 隐式本构积分算法示意Fig.2 The diagram of implicit integration algorithm

通常，初次回拉应力σC不会在残余强度屈服面上，为此采用隐式向后欧拉算法，通过多次迭代计算使σC准确位于残余强度屈服面fr上。以下省略公式中下标C表示为当前构型的应力状态，对式(26)进行微分，并化简得到：

式中：I为单位矩阵；为相较初始Δεn的改变量；为相较初始σC的改变量；为相较Δλ的改变量。

根据屈服函数f的一致性条件，为了使当前应力σ落在残余强度屈服面上，应使=0，即：

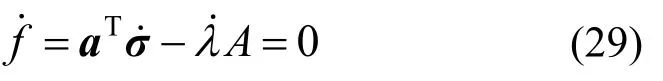
将式(29)代入式(28)，并化简得到：

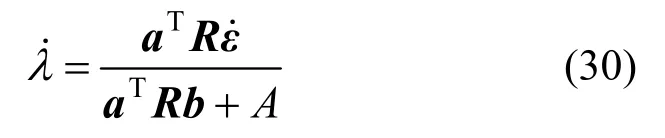
将式(30)代入式(28)中，即可得到一致性切线模量Dct：

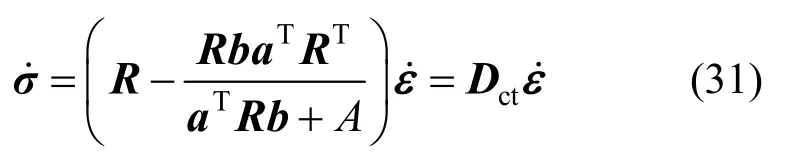
通过多次回拉计算，最终满足下述方程组，使σC准确位于残余强度屈服面上：

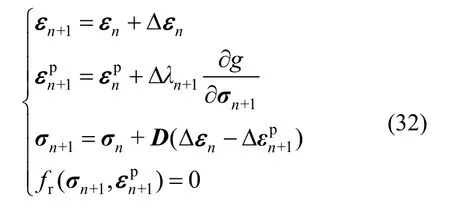
在隐式应力更新过程中，涉及到屈服函数f及塑性势函数g对应力σ的求导，具体计算公式可参见文末附录。

2.2 H-B准则理想弹塑性隐式本构积分算法

H-B准则理想弹塑性的隐式本构积分算法，与脆塑性隐式本构积分算法相近，也可按照式(25)～式(32)进行理想弹塑性应力更新，区别仅在于式中屈服函数取峰值强度面屈服函数，不再进行赘述。

采用FORTRAN语言，将上述H-B准则脆塑性及理想弹塑性隐式本构积分算法编入有限元软件ABAQUS中，并按照一系列应力跌落-塑性流动，实现H-B准则应变软化模型求解。

3 数值算例验证

H-B准则常见的应用之一是判别山岭隧道开挖后围岩的稳定性，因此其数值实现的验证常基于如图3(a)所示的一类经典弹塑性力学问题，即计算处于平面应变状态的应变软化圆隧围岩的力学响应规律，并与解析解对比，有限元模型见图3(b)。

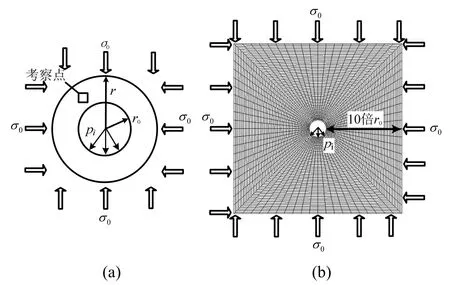
图3 围岩力学响应理论模型及有限元模型Fig.3 Example of a circular tunnel excavation and finite element model

基于H-B准则，根据表1中计算参数(上标p表示峰值强度参数，上标r表示残余强度参数)，遵循强度参数和剪胀角随塑性剪应变η分段线性演化规律，Lee等[24]提出将塑性区按相等的应力增量划分，围压逐渐递减的差分方法；Wang等[25]及Zhang等[26]提出了将软化区划分成若干个弹脆性模型，从弹塑性交界面逐步计算至洞壁，给出了应变软化圆隧围岩力学响应规律解析解，见图4。为了检验模型的合理性，将本文通过ABAQUS有限元计算的圆隧收敛位移及应力分布也绘于图4。

表1 文献[24-26]中应变软化圆隧围岩计算参数Table 1 Calculation parameters of tunnel rock mass material exhibiting strain softening behavior in reference [24-26]

观察图4(a)可以发现，本文计算的围岩特征曲线与Lee等[24]、Wang等[25]及Zhang等[26]解析解十分接近；图4(b)中，本文计算的pi=0时的围岩径向及切向应力分布与Lee等[24]及Wang等[25]的解析解也具有较好的可比性，说明本文所述的数值实现工作在整体模型层次是正确有效的，扩展了ABAQUS功能。

图4(b)中切向应力分布解析解与本文有限元解存在一定的差异，一方面，可能是因为解析解在计算过程中，每一个微元的切向应力取跌落前和跌落后的平均值，而本文采用有限元计算结果；另一方面，也可能与采用的脆塑性计算步数有关，出于计算效率考虑，本文在计算过程中，设置了100个脆性跌落-塑性流动计算步，脆塑性计算步越多，峰后模拟曲线与试验结果越接近。

图4 不同方法计算结果对比Fig.4 Comparisons of calculation results by different methods

4 工程应用

4.1 工程概况

某盾构输水隧洞工程采用双线形式布置，隧洞设计断面为圆形，盾构外径6 m，两洞室平行布置，中心间距12 m。混凝土管片衬砌内径为5.4 m，厚0.3 m，宽1.5 m。

选取埋深42.5 m的某一洞段作为研究对象，该洞段上覆弱风化岩层厚3 m，上部为土层。根据规范[27]，进行运行期承载能力极限状态分析，内水压力水头为196 m，外水压力水头为18 m，地应力按自重应力场考虑。

4.2 计算参数及有限元模型

不考虑衬砌透水，土体及管片衬砌采用线弹性模型，围岩采用所建H-B准则应变软化模型及理想弹塑性模型，管片与管片之间、管片与围岩之间接缝采用库伦摩擦模型，接缝面之间可以传递压应力和小于临界切向力的剪应力，不能传递拉应力。具体力学参数见表2，假定围岩强度参数及剪胀角随塑性剪应变分段线性变化，临界塑性剪应变为0.2×10−3。

表2 围岩、管片衬砌及土层力学参数Table 2 Calculation parameters of surrounding rock, segment lining and soil

有限元模型沿洞轴向取4环管片长度，四周边界均取3倍洞径，顶部超出部分土层作为均布压应力施加在上表面。与洞轴向垂直、平行的边界面均沿其面法向施加水平链杆约束，底面施加垂直链杆约束，有限元模型网格见图5。

4.3 计算结果及分析

计算步骤为：① 建立初始地应力平衡；② 左、右隧洞同时开挖；③ 施作管片衬砌，施加内水压力及外水压力。

隧洞开挖完成后未出现塑性变形，由围岩承受全部开挖应力释放荷载。施加管片衬砌，内、外水压力分别作用在管片内外侧。鉴于有限元网格及荷载对称，仅以右洞为例，分析围岩的变形破坏。

1) 围岩拉应力对比分析

观察图6所示围岩拉应力对比可以发现，采用应变软化模型计算的隧洞顶部及底部围岩拉应力，明显低于采用理想弹塑性模型的计算结果，这主要是因为在考虑应变软化情况下，随着围岩塑性屈服，其承载能力逐渐下降，应力发生转移。

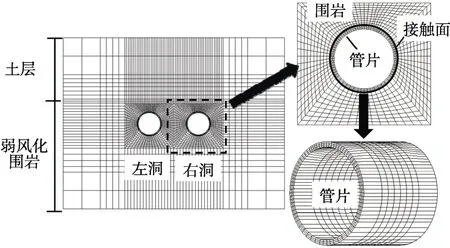
图5 有限元模型网格Fig.5 The finite element model

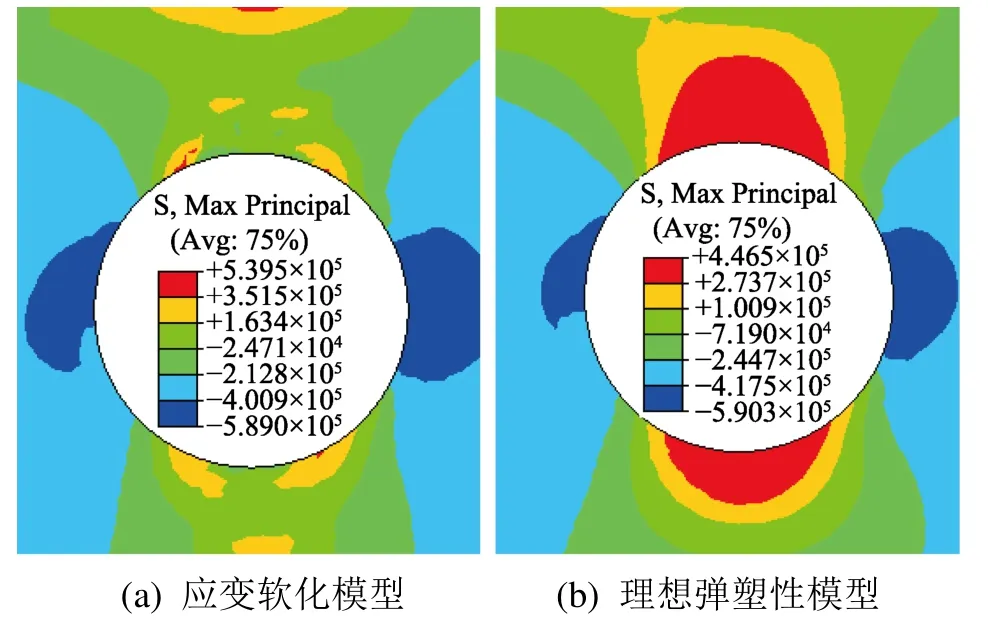
图6 围岩拉应力对比Fig.6 Tensile stress distribution of surrounding rocks

2) 围岩塑性区对比分析

图7中采用应变软化模型和采用理想弹塑性模型计算的围岩塑性开裂区范围差异明显，采用理想弹塑性模型计算的顶部围岩塑性区深度为1.6 m，未贯穿上覆盖岩层，认为输水隧洞是安全稳定的；而采用应变软化模型计算的顶部围岩塑性区贯穿上覆盖岩层，整体结构接近失稳破坏。显然，以理想塑性计算的结果是偏危险的，而应考虑岩石峰后塑性软化效应。

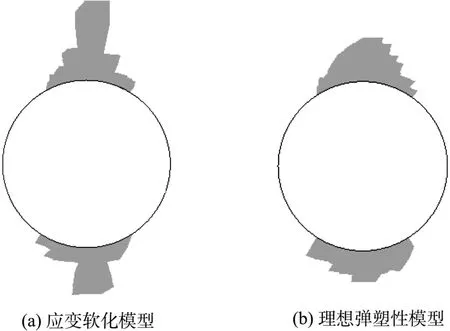
图7 围岩塑性区对比Fig.7 Plastic zone distribution of surrounding rocks

从考虑峰后软化效应的计算结果来看，在给定内水压力作用下，即使围岩与管片衬砌共同工作，由于上覆岩层过薄，难于满足安全要求。处理的方法可考虑在管片衬砌内侧增加钢筋混凝土衬砌，或增加钢板衬砌。

5 结论

(1) 对当前不同脆塑性计算方法的合理性进行分析，发现塑性位势跌落可正确计算岩石不同类型破坏，而偏应力等比例跌落和最小主应力不变跌落均存在不足。

(2) 推导给出基于塑性位势跌落的H-B准则脆塑性隐式积分算法，及H-B准则理想弹塑性隐式积分算法，并采用一系列脆性跌落与塑性流动，将H-B准则应变软化模型嵌入有限元软件ABAQUS中。

(3) 比较应变软化圆隧围岩收敛位移及应力分布的解析解与本文有限元解，发现二者吻合良好，说明本文所述的数值实现工作在整体模型层次是正确有效的，扩展了ABAQUS功能。

(4) 对某薄上覆盖层高内水压输水隧洞的计算结果表明，相较理想弹塑性模型，所建应变软化模型可更合理地描述围岩塑性破坏及应力调整过程，反映隧洞顶部围岩塑性区贯通引起的整体结构失稳破坏现象，为工程选择衬砌方案提供依据。

附录：

选取σ1＞σ2＞σ3区间进行分析，当应力位于π平面棱线或顶点时，可进行单独处理，具体可参考文献[6, 14]。由于脆塑性隐式本构积分算法与理想弹塑性本构积分算法，屈服函数f及塑性势函数g的求导相同，故统一表示如下：

1) 屈服函数f一次求导的表达式如下：

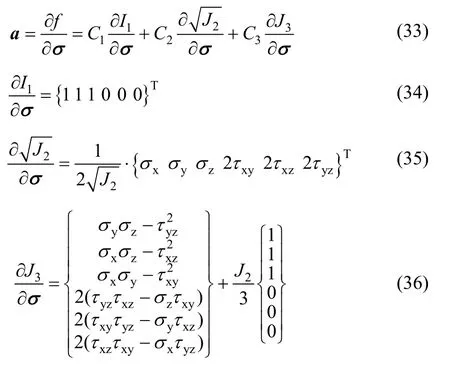
其中：

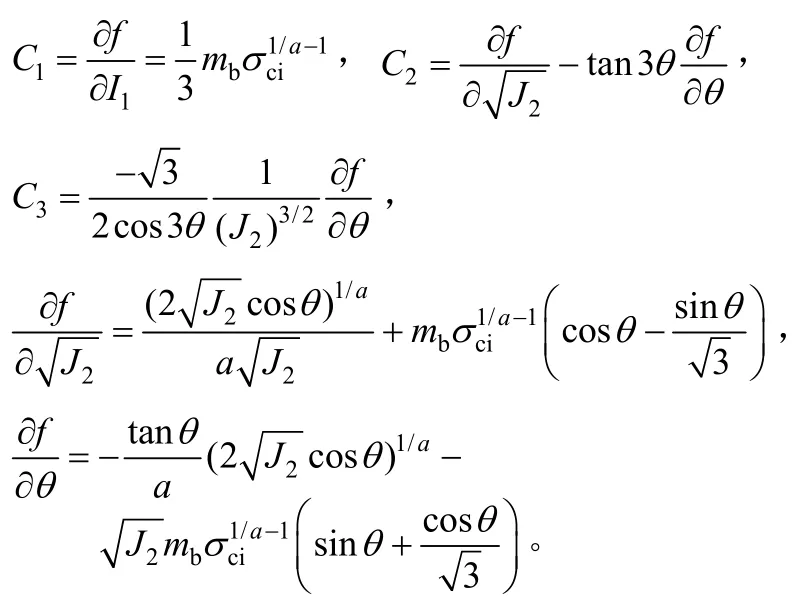
2) 塑性势函数g一次求导的表达式如下：

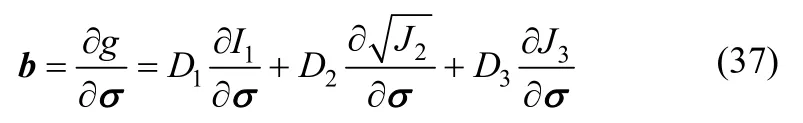
3) 塑性势函数g二次求导的表达式如下：

其中：