Koch曲线的Hausdorff测度的改进上界估计
郭东亮
(中山大学 电子与通信工程学院,广东 广州 510006)
在分形几何研究中,分形的Hausdorff维数与Hausdorff测度的确定非常重要[1].对于一般集合来说,计算其Hausdorff测度难度很大,不存在普遍适用的计算方法.满足开集条件的自相似分形集由于具有严格的自相似性,其Hausdorff维数和Hausdorff测度的计算相对简单,因而研究成果最多.Cantor集、Koch曲线和Sierpinski垫片是3个经典自相似集,目前三分Cantor集的Hausdorff维数与Hausdorff测度已经得到完全解决[1],但Koch曲线和Sierpinski垫片的Hausdorff测度则难以计算出准确值,只能估计其上下界.本文在已有研究成果基础上,通过构造更加精细的新覆盖并利用相关定理,得出Koch曲线的Hausdorff测度的更好上界估计.
1 Koch曲线及其Hausdorff测度
1.1 Koch曲线
设K0是Euclid平面R2上的单位线段[0,1],将K0三等分,以中间的1/3线段为底边作正三角形,再去除底边的内部,得到一条由4个长度为1/3的边组成的折线,记为K1,对K1的每个边重复上述过程,得到42个长度为1/32的边组成的折线,记为K2,重复以上过程,得到折线序列K0,K1,K2,…,Kn,当n→时,此折线序列趋于一条曲线K,称其为Koch曲线,它是典型的规则分形.关于Koch曲线K有如下一些相关定义和结果[1-2]:
(1)K是由压缩比为1/3的相似压缩定义的,其Hausdorff维数s=log34.
(2)设n≥1,Kn中夹角为60°的相邻两边构成一个正三角形,称作Kn的基本三角形,并记作△n.
(3)K是路径连通的,设点A、A′∈K,记AA′为K上从点A到点A′的连通弧.
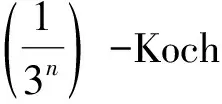
1.2 相关引理
引理1[1]由Hausdorff测度Hs(K)的齐次性知
引理2[2]设U⊂Rn为可测集,|U|>0,F是满足开集条件的自相似集,则
2主要结果及证明
图1所示为K的局部图形,其中,|AA′|=1/3,点A、O、A′为K1中的折线点,点E、E′为K2中的折线点,B、D、F为K4中的折线点,文献[2]正是基于K4构造了七边形BDEOE′D′B′作为覆盖(E′、D′、B′分别为E、D、B关于直线OO′的对称点),考虑K上的连通弧BB′,推导K的Hausdorff测度上界.将点B附近的图形放大,得到图2,在属于K4的边FB上生成属于K5的正三角形△GHI,再在属于K5的边GB上生成属于K6的正三角形△JLM,文献[3]和文献[4]分别将九边形JMDEOE′D′M′J′作为新覆盖(M′、J′分别为M、J关于直线OO′的对称点),并考虑K上的连通弧MM′,推导出K的Hausdorff测度的更好上界.
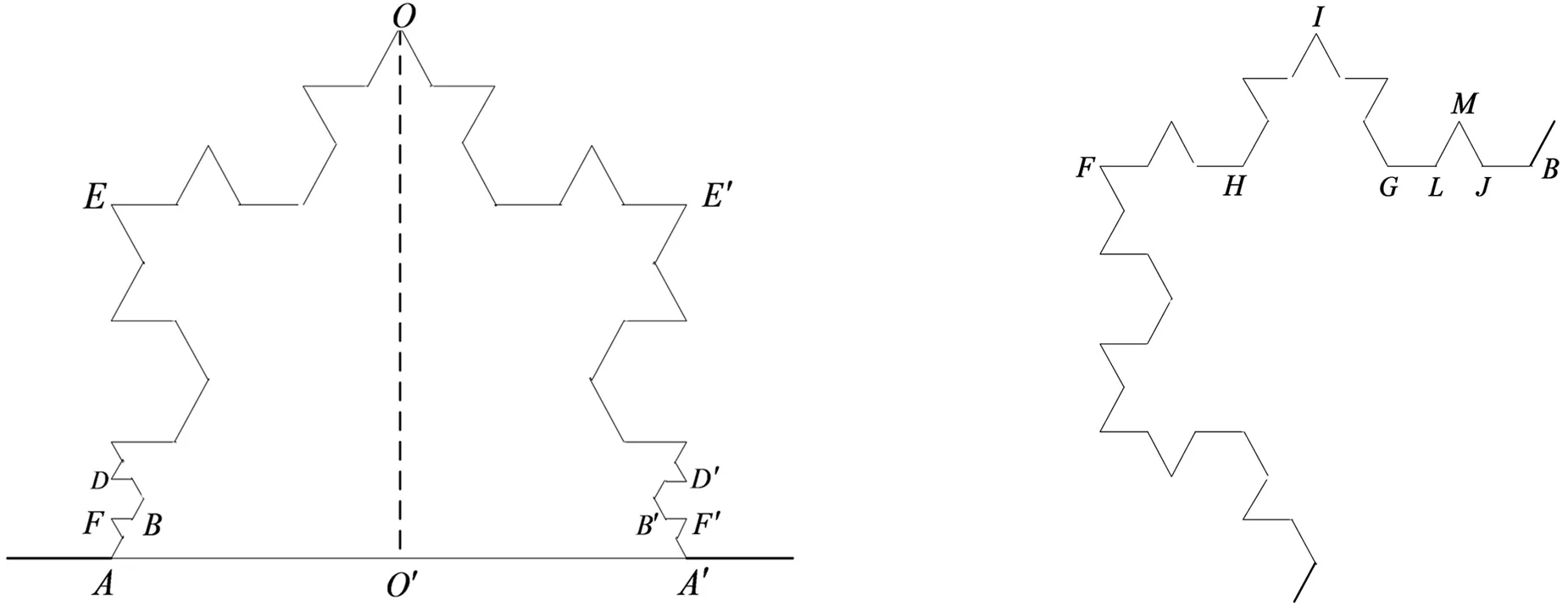
图1Koch曲线局部示意图(K4) 图2Koch曲线局部示意图(K6)
Fig.1LocalsketchofKochcurve(K4)Fig.2LocalsketchofKochcurve(K6)
放大边LB段的图形,得到图3,其中正三角形△NPQ属于K7,正三角形△RST属于K8,文献[5]基于K7上的连通弧构造新覆盖,将K的Hausdorff测度上界进一步减小至Hs(K)≤0.587 697,该上界是已公开发表文献中的最好上界.
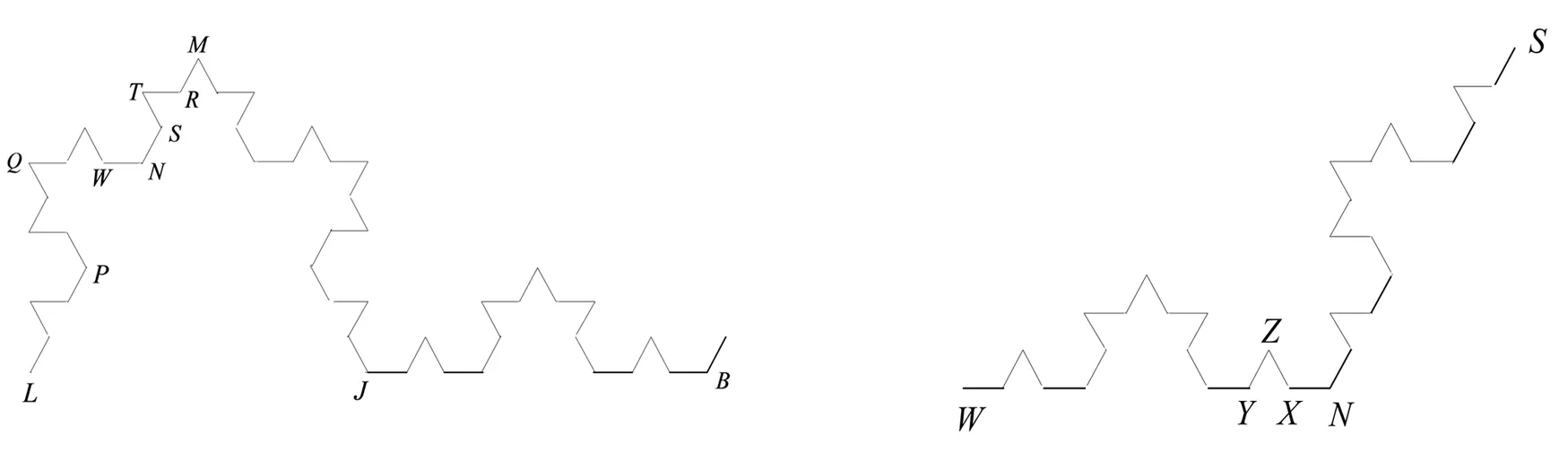
图3 Koch曲线LB段局部示意图(K8) 图4 Koch曲线W-N-S段局部示意图(K10)
Fig.3LocalschematicdiagramofLBFig.4LocalschematicdiagramofW-N-SsectionofKochcurve(K8)sectionofKochcurve(K10)
定理Koch曲线K的Hausdorff测度Hs(K)<0.587 650.
证明放大边W-N-S段的图形,得到图4,其中正三角形△XYZ属于K10,将11边形NXZDEOE′D′Z′X′N′作为新覆盖(N′、X′、Z′分别为N、X、Z关于直线OO′的对称点),记为U,并考虑K上的连通弧ZZ′,易见K∩U=ZZ′.下面分析本文提出的新覆盖U的直径.
由于基本三角形△i的一条边的长为1/3i,i=1,2,3,…,因此有
由图4可以算得
因此,新覆盖U的直径仍是|DE′|.
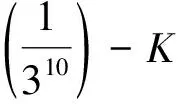
由引理1,得
由引理2,得
此为迭代至K10时,Koch曲线K的Hausdorff测度的上界估计值,也是目前已知的最好上界.
3 结 论
通过构造更加精细的新覆盖,研究了新覆盖与Koch曲线的交集对应的连通弧,并利用相关定理计算出了Koch曲线的Hausdorff测度的更好的上界估计值Hs(K)≤0.587 650.
——从广州一模的一道选择题谈起

