基于自适应层次谱聚类与遗传优化的TSP算法
杨彩虹, 杨明
(1.中北大学 理学院,山西 太原 030051;2.信息探测与处理山西省重点实验室,山西 太原 030051 )
1 引 言
旅行商问题(TSP)是一个经典的NP难度的组合优化问题,也是计算机科学和地理信息科学等许多领域的研究热点[1-4].大规模的TSP得到最优解非常困难,因此人们提出了许多近似解法,但由于这些算法的自身缺陷,获取的近似解可能会远远偏离于最优解[5],而且许多实际问题不能在有效的时间内找到相对较优的解,促使启发式算法的出现,如遗传算法[6]、粒子群优化算法、蚁群优化算法[7-8]、人工神经网络、进化策略、进化编程、禁忌搜索和免疫计算[9]等.
遗传算法是建立在自然选择和自然遗传机理基础上的迭代自适应概率性搜索算法[6],它的优点在于能很好地处理约束,鲁棒性强,具有潜在的并行性,全局搜索能力强;缺点是收敛较慢,甚至迭代难以收敛,局部搜索能力弱,运行时间长,当问题规模较大时,迭代过程中会占用很大的内存空间,再加上遗传算子中的交叉算子使得染色体之间具有很大的相似性,可能导致搜索停滞不前,使种群多样性减少,同时,由于变异的力度不够,遗传算法的爬山能力很弱,导致种群多样性得不到补充,使算法出现早熟特征[5-6].针对传统遗传算法出现的收敛慢及早熟现象,提出了一种基于自适应层次谱聚类与遗传优化算法求解大规模TSP.
2 自适应层次谱聚类
为提高大规模TSP的求解效率,首先对数据集进行聚类,将大规模TSP转换为一个GTSP和多个小规模TSP的求解,针对聚类后数据集规模的不确定性以及传统谱聚类高斯核函数尺度参数的影响,提出了利用自适应层次谱聚类的方法,该算法首先构建出一种基于测地距离和局部密度的自适应相似矩阵,并应用到谱聚类算法中实现城市的初步聚类,当聚类城市规模超过设定阈值,用上述自适应谱聚类算法进行层次聚类,直到每类城市规模均小于阈值时停止聚类.
2.1 自适应相似矩阵的构建
谱聚类算法的核心思想是对待聚类数据点的相似矩阵(拉普拉斯矩阵)进行特征分解,并对其特征向量聚类,因此相似矩阵的构建很大程度上影响了聚类的效果.
2.1.1 距离函数
谱聚类在构建相似性矩阵时,距离函数的选择尤为重要.测地距离是由Tenenbaum等人最早提出[10],可以有效表示流体结构上数据点间的真实距离,故选择测地距离作为距离函数可提高聚类精度.测地距离计算过程:
1)输入数据集X=[x1,x2,…,xn],并求得每个数据点的l个欧式近邻点;
3)任两点测地距离
(1)
其中T=[1,2,…,n].
2.1.2 局部密度
根据文献[11] 提出的基于共享近邻的相似性度量聚类,可利用两点间的共享近邻来表示两点间的局部密度
Dens(xi,xj)=|n(xi,p)∩n(xj,p)|
(2)
其中,n(xi,p)为距离xi最近的前p个点,n(xj,p)为距离xj最近的前p个点.一般地,取共享近邻数p=round(样本数×3%).
2.1.3 自适应相似矩阵
为消除传统谱聚类高斯核函数尺度参数的影响,构建了一种密度自适应的相似矩阵S=[sij]n×n,其中
(3)
其中,σi=norm((xi-xil),2)表示数据点xi到其第l个最近邻样本点xil的欧式距离,σj=norm((xj-xjl),2)表示数据点xj到其第l个最近邻样本点xjl的欧式距离,一般地,取l=7[12-13].
2.2 自适应谱聚类过程
Step 1输入数据集X=[x1,x2,…,xn];初始聚类个数k;
Step 2构造自适应相似矩阵S=[sij]n×n;

Step 4求L的前k个最大特征值对应的特征向量ξ1,ξ2,…,ξk,构造特征矩阵E=[ξ1,ξ2,…,ξk]n×k,并将矩阵E的行向量单位化得矩阵U;
Step 5将矩阵U的每个行向量对应到原数据集的相应点,并利用K-means将其聚类,得到C1,C2,…,Ck.
2.3 自适应层次谱聚类流程
Step 1输入数据集X=[x1,x2,…,xn];根据数据集规模设定初始聚类个数k,以及城市规模阈值thvalue;
Step 2利用自适应谱聚类算法将数据集X进行初始聚类,得到C1,C2,…,Ck;
Step 3若|Ci|>thvalue,i∈[1,2,…k],其中|Ci|表示类Ci中数据点个数,利用自适应谱聚类算法将Ci聚为两类得到类Ci1,Ci2;反之,则不再次进行聚类;
Step 4若|Cit|>thvalue,t∈[1,2],则对Cit重复Step3,直到满足层次聚类终止条件|Cit| Step 5通过上述操作,最终形成新类群C1,C2,…,Ck,…,Cs,其中s≤k. 自适应层次谱聚类将大规模TSP转换为一个GTSP和多个小规模的TSP,针对该问题的求解提出了一种基于最近邻、禁忌搜索和传统遗传算法的改进遗传算法. 采用路径表示法,种群中每个染色体长度为n,染色体中的每个基因由1~n的数字组成,且为1~n的全排列. 判断TSP可行解的优劣的标准是看其适应度函数的值,本研究用其目标函数值的倒数作为其适应度函数的值,即 (4) 当Fitness(x)越大,F(x)值越小,对应TSP解越好. 3.3.1 种群选择策略 采用精英保留策略,此方法是比较种群中所有个体的适应度值,从中择优选择一部分个体作为父体,并利用选择的个体进行交叉和变异操作. 3.3.2 交叉 交叉是父代将自身优秀基因遗传给子代的一种操作.常用交叉算子有顺序交叉(Ordered Crossover,OX)、部分映射交叉(Partially Mapped Crossover,PMX)和循环交叉(Cycle Crossover,CX)[14];改进算法选择顺序交叉算子,在父代F1中随机选择两个交叉点,将父代F1交叉点之间的基因片段作为子代K相同位置的基因片段,把F2中非F1交叉点之间的基因按顺序分别放在子代K的基因片段两边的位置,生成新的子代个体.以染色体长度n=10为例,选择父代F1、F2,若随机选择交叉点位置为4、7,则具体交叉操作如下: 3.3.3 变异 变异是保留父代优秀基因并保持种群多样性的一种进化手段.常用变异算子有:移位变异(Displacement Mutation,DM)、交换变异(Exchange Mutation,EM)和逆转变异 (Inversion Mutation,IVM)[14];改进算法采用交换变异算子进行变异操作,随机作用在一个父代染色体上,在父代F中随机选择四个变异点,按升序排列n1 父代F:6(5 1)7 4 2(10 3 8)9 子代K:6(10 3 8)7 4 2(5 1)9 最近邻算法生成的路径的基因总体比较优良,而禁忌搜索能够增强遗传算法的爬山能力,因此设计了结合最近邻和禁忌搜索思想的改进遗传算法来求解TSP. 改进遗传算法的流程如下: Step 1设定种群大小Numpop、设定交叉概率crate、变异概率mrate、选择率srate和随机概率rrate,并且设定算法的终止条件r=Iteration,设置进化代数r=0,禁忌表tabu=[]; Step 2将每一个个体作为出发点,由最近邻算法生成的路径所构成的集合记为P,并计算个体的适应度,从P中随机选择Numpop个个体初始化第一代种群S(r); Step 3更新禁忌表tabu,禁忌表中存放已经搜索过的路径; Step 4择优选择,比较种群S(r)中所有个体的适应度值,从中择优选择一部分个体作为父体F; 图1 改进遗传算法流程图 Step 7更新父代和子代的并集Srecent(r); Step 8随机生成新的路径S*(r),且新的路径不与禁忌表中路径重复(引入新个体,增加种群多样性); Step 9r←r+1,在Srecent(r)∪S*(r)择优选择Numpop个个体作为新的种群S(r); Step 10若满足终止条件,则停止并输出最短路径F(xbest);否则转step3. 为提高大规模TSP的求解效率,首先利用自适应层次聚类算法对数据集进行聚类,将大规模TSP转换为对一个类间最短路径的求解和多个类最短路径的求解,即GTSP和小规模的TSP的求解. 类间最短路径求解即为GTSP的求解,GTSP的一个可行解即为类与类之间的连接顺序. 定义1.类Ci与类Cj之间的距离函数: Dij=D(Ci,Cj)=min{d(x1,y1),d(x1,y2),…,d(x1,yr), d(x2,y1),d(x2,y2),…,d(x2,yr),…,d(xt,y1),d(xt,y2),…,d(xt,yr)} (5) 其中,x1,x2,…,xt表示Ci中的数据点,y1,y2,…,yr表示Cj中的数据点,d(xt,yr)表示两个数据点的欧氏距离. 定义2.两个类之间欧式距离最小的两个点即分别为两个类的边界点,即: d(x2,y1),d(x2,y2),…,d(x2,yr),…,d(xt,y1),d(xt,y2),…,d(xt,yr)} (6) 则 分别为类Ci,Cj的边界点. 设该GTSP模型集合为G=(V,E),其中V={1,2,…,s},1~s表示类标号;E为类间连线的集合,边(i,j)的权值为Dij,i,j∈V,在该问题中,Dij取(5)式定义的距离函数;类间路径的优化是寻找G的最短巡回路线,该巡回路线是类间连线最短回路,且最终在每个类中均可找到两个类边界点.经过图V集中每个类顶点恰好两次(每类有两个边界点),即寻找经过V集的不同类边界点连线的最短巡回线路,图2为类边界点连线示意图. 图2 类边界点连线示意图 则类间最短路径总长度 FC(Xopt)=min{FC(X)} (7) 其中FC(x)为类间路径总长度,且 (8) 其中,i,j∈V,i≠j,而 (9) 类内最短路径求解即是对TSP的求解,本文采用自适应层次聚类算法将数据点聚为C1,C2,…,Ck,…,Cs,则类内最短路径的求解即为对s个TSP的求解.以类Ci为例,其最短路径为: FCi(Xi)=min{FCi(Xi)} (10) (11) (12) 结合类间和类内最短路径的建立过程,可建立大规模TSP的数学模型: (13) 其中s为聚类总数,采用本文提出的改进遗传算法进行求解. 为了验证提出的基于自适应层次谱聚类与遗传优化的算法的性能,在仿真环境Intel(R)Core(TM).i5-2450M CPU、4.00 GB RAM、Window7(32bit)、MATLAB r2013a下,采用本文算法和传统遗传优化算法,选用TSP标准测试库TSPLIB[15]中的问题进行数值实验.在实验中,两算法参数设置相同,设置如下:种群大小Numpop=120、交叉概率crate=0.9、变异概率mrate=0.2、选择率srate=0.3、随机概率rrate=0.3和城市规模阈值thvalue=200,且设定类内进化代数、类间进化代数以及遗传算法进化代数均为Iteration =300.表1为9个不同TSP实例的遗传算法和本文算法实验数据,9个TSP实例数据规模分别为150、198、280、417、535、783、1 000、1 379和5 915,数据整体呈递增趋势.由表1可以看出本文算法的最优解均优于遗传算法最优解,运行时长更短,且遗传算法结果误差在10%~22%之间,本文算法结果误差在3%~11%之间.图3直观地展示了两算法在相同参数时,9个不同TSP实例的结果误差和运行时间的折线图.由图3(a)知,本文算法的结果误差总体小于遗传算法误差,且随着数据规模的增大,本文算法的结果优势更明显;由图3(b)知,本文算法的运行时间均小于遗传算法运行时间,当数据规模增大时,两算法运行时间整体呈上升趋势,且本文算法在TSP数据规模增大时,用时优势更加明显.由此可见,本文算法针对大规模TSP,有效避免收敛速度慢以及早熟现象,较大程度减少了运算时间,提高了计算效率. 表1不同TSP实例遗传算法与本文算法实验结果 Table1DifferentTSPinstancesresultsofgeneticalgorithmandadaptivehierarchicalclusteringgeneticalgorithm 序号TSP问题最优解 GA算法 本文算法 解误差/%运行时间/s解误差/%运行时间/s1ch1506 5287 20510.377156 874655.302d19815 78018 44116.861 39916 5901275.133a2802 5793 03617.725472 8433810.244fl41711 86113 80216.361 39412 2091102.935ali535202 339230 05813.70845214 9771536.256rat7838 80610 70921.612389 376826.477dsj100018 659 68822 449 66520.311 34620 382 0567219.238nrw137956 63868 32720.648 01362 3371 33210.069rl5915565 530684 58421.0510 472583 7252 3483.22 (a)遗传算法与本文算法结果误差折线图 (b)遗传算法与本文算法运行时间折线图 图3不同TSP实例遗传算法与本文算法比较 Fig.3DifferentTSPinstancescomparisonofgeneticalgorithmandadaptivehierarchicalclusteringgeneticalgorithm 提出了一种基于自适应层次谱聚类与遗传优化的TSP算法,该算法首先构建一种自适应相似矩阵,并应用到谱聚类算法中实现城市的初步聚类,当聚类城市规模超过设定阈值,用上述自适应谱聚类算法进行层次聚类,直到每类城市规模均小于阈值,从而将大规模TSP转换为一个GTSP和多个小规模TSP;其次,利用结合了最近邻与禁忌思想的改进遗传算法求GTSP的最优解;最后,用改进遗传算法求各个小规模TSP的最优解;综合GTSP和各TSP的最优解,即得大规模旅行商问题的最优解.改进遗传算法采用最近邻算法选取一系列好的初始种群,加快了种群的搜索速度,同时将禁忌搜索中“禁忌”的思想引入到遗传算法中,使得种群在进化过程中保证了多样性,增强了算法的爬山能力,避免了算法出现早熟.选取TSP标准测试库TSPLIB中不同分布的数据集进行数值实验,结果表明该算法达到了预期的结果,可以将该算法运用到实际的生产生活中.3 改进遗传优化算法
3.1 算法编码方式
3.2 适应度函数的选择
3.3 种群选择策略、交叉和变异
3.4 改进遗传算法流程
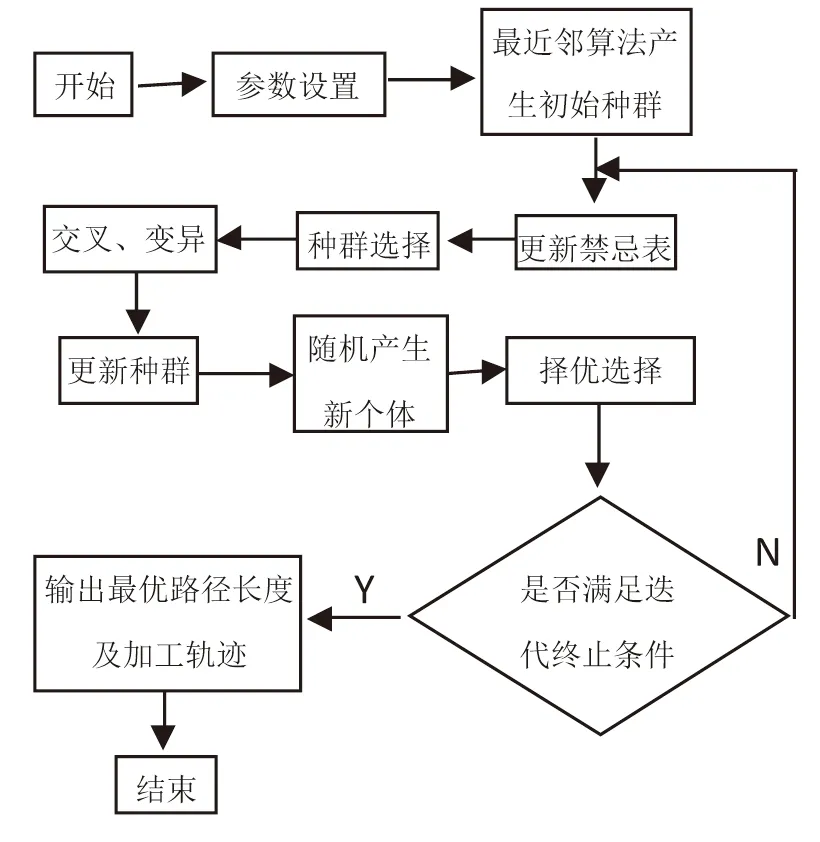
4 大规模TSP的求解
4.1 类间最短路径
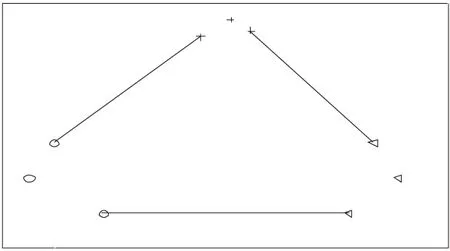

4.2 类内最短路径模型建立
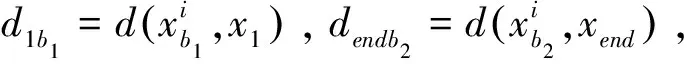
4.3 大规模TSP模型建立与求解
5 数值实验

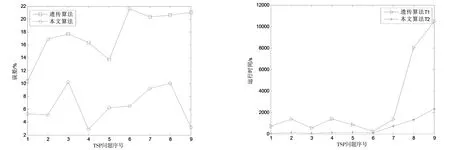
6 总 结
——基于人力资本传递机制

