应力波反射法判定缺陷程度的量化计算

陈仕坤

（广东惠和工程检测有限公司 广东广州 510410）

1 缺陷程度的量化计算

假设桩在x～x+△x处有一理想缺陷段[1]，见图1，桩顶入射波为V0，缺陷透射波为V。桩身缺陷界面Ⅰ（上界面）的入射波为Vi，反射波为Vr，桩身阻抗为Z1，缺陷段阻抗为Z2，阻抗比即桩身完整性系数）[2]。

图1 桩身缺陷

当桩顶入射波V0沿着桩身向下传播[3-4]，桩身材料阻尼引起的阻力波幅值衰减符合指数规律，桩身阻尼系数为a，桩周土阻力引起的阻力波导致的速度衰减值为Vs1，令e-αx=φ则有：

其中：x——缺陷位置到桩顶的距离；

C——波速；

△t——缺陷反射波与桩顶入射波峰的时间差。

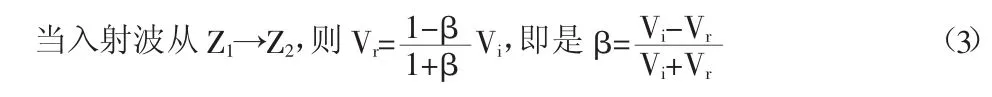
当反射波Vr沿着桩身向上传播[3-4]，桩身材料阻尼引起的阻力波幅值衰减符合指数规律，桩身阻尼系数为a，桩周土阻力引起的阻力波导致的速度衰减值为Vs2，并注意到桩顶为自由端，速度加倍，则有V=2×（αx-Vs2）=2×（φVr-Vs2），则：

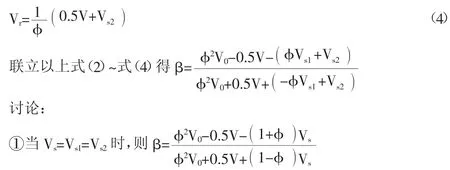
②当不考虑桩周土对应力波传播的影响时，即是Vs1=0，Vs2=0，则：

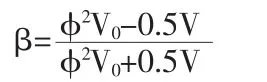
③不考虑桩身阻尼对应力传播的影响时，即是φ=1，则：

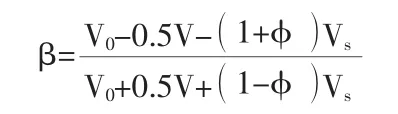
④不考虑桩周土对应力波传播的影响且不考虑桩身阻尼对应力传播的影响时，即是 Vs1=0，Vs2=0，φ=1，则 Vi=V0，Vr=0.5V，β==-1，其中 n=，引用DBJ 15-60—2019《建筑地基基础检测规范》高应变判定桩身完整性判定依据得表1所示。

表1 依据缺陷透射波速度V与桩顶入射波V0的比值n判定桩身完整性

表2 依据缺陷透射波速度V与桩顶入射波V0的比值n判定桩身完整性

许多检测领域的同行在判定缺陷反射波的幅度时，直接采用缺陷透射波速度V（陷透射波速度V未进行指数放大）与桩顶入射波V0的比值确定，认为有以下观点：①当=0时，为Ⅰ类桩；②当0＜时，为Ⅱ类桩；③当时，为Ⅲ类桩；④当时，为Ⅳ类桩。虽然界限数值和表1比较接近，但笔者认为上述观点并无严格的理论及实践依据，表1的界限数值0.222、0.5已经导致桩身缺陷程度被轻判，若采用界限数值则桩身缺陷程度更被轻判，检测结果严重失真，故对上述观点持否定态度。

2 工程实例

实例1：一根有缺陷的桩，桩身应力波波速为C=4000m/s，质量密度2.4t/m3，桩面传感器测得的反射波时域曲线如图2所示。

图2 桩面传感器测得的反射波时域曲线

入射波（半正弦脉冲）V1=V0e-αx，t∈[0，1]ms，V0=2mm/s

缺陷反射波（半正弦脉冲）V2=V0sinωt∈[10，11]ms

假设桩周土阻力和桩身材料阻尼引起的阻力波幅值衰减符合指数规律a=0.02/m，（x为应力波行进的距离）[3]。请结合高应变判定桩身完整性判定依据，不考虑其他因素，纯粹量化判断桩身完整性类别。

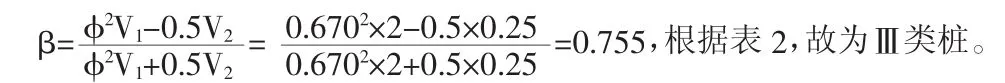
实例2：一根有缺陷的桩，桩身应力波波速为C=4000m/s，质量密度2.4t/m3，桩面传感器测得的反射波时域曲线如图3所示。

图3 桩面传感器测得的反射波时域曲线

入射波（半正弦脉冲）V1=V0sinωt，t∈[0，1]ms，V0=2mm/s

不考虑桩周土阻力和桩身材料阻尼对应力波的影响。请结合高应变判定桩身完整性判定依据，不考虑其他因素，纯粹量化判断桩身完整性类别。

由于缺陷反射波（半正弦脉冲）V2=V0sinωt，则桩面传感器测得的速度幅值为V0=×2=0.25mm/s

由于缺陷反射波（半正弦脉冲）V2=1V0sinωt，则桩面传感器测得的8速度幅值为V0=×2=0.25mm/s

3 结语

本文判定缺陷程度的量化计算亦存在局限性：①桩周土阻力引起的阻力波导致的速度衰减值Vs、桩身材料阻尼系数a目前研究不足，特别对于多层桩周土时，试图量化桩周土阻力引起的阻力波导致的速度衰减值Vs会存在较大的困难[5]；②缺陷段长度△x太小，则界面Ⅱ（下界面）产生的压缩波，削弱界面Ⅰ（下界面）产生的拉伸波，导致无法准确判断界面Ⅰ（下界面）的缺陷程度；③桩身缺陷段△x上下附近位置存在其他缺陷时，动测仪采集间隔过大，也导致无法准确判断界面Ⅰ（下界面）的缺陷程度。