Cn-平坦模的一些结果

王 茜，王芳贵，沈 磊

(1.四川文理学院 数学学院, 四川 达州 635000;2.四川师范大学 数学与软件科学学院, 四川 成都 610066)

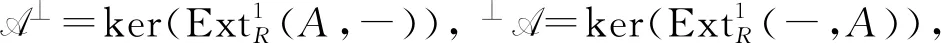
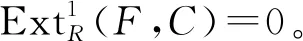
1 Cn-平坦模及其基本性质

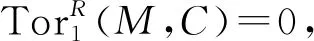
下面的事实是显然的。

注1①平坦右R-模是Cn-平坦模；

②当m≥n≥0时, 由于Fn⊆Fm, 故有Cm⊆Cn, 因此,CnF⊆CmF;

③由于I ⊆Cn, 故Cn-平坦模是余纯平坦模。

命题1模类CnF对直和与直和加项是封闭的。

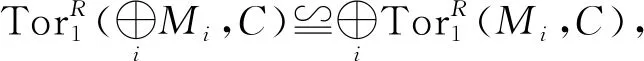
定理1对右R-模M, 以下各条等价:

①M是Cn-平坦模;

②M+是Cn-内射模;

③设ξ:0→A→B→C→0是左R-模正合列，若C∈Cn, 则M⊗Rξ也是正合列;

④任何形如0→A→B→M→0的右R-模正合列是Cn-纯正合列。

①⟹③显然。

③⟹①设C∈Cn, 考虑正合列ξ:0→K→F→C→0, 其中F是平坦模，则有正合列

④⟹①考虑正合列η:0→K→F→M→0, 其中F是平坦模。对任何C∈Cn, 则有正合列

命题2设0→L→M→N→0是右R-模正合列，若L,N是Cn-平坦模, 则M也是Cn-平坦模, 即模类CnF关于扩张是封闭的。

设L是R-模类,M∈L,X是R-模,φ:X→M是同态。若对任何N∈L, 以及同态g:X→N, 恒有同态h:M→N, 使得g=hφ, 则称(M,φ)为X的L-预包。显然,φ:X→M是X的L-预包当且仅当对任何N∈L, 诱导同态φ*:HomR(M,N)→HomR(X,N)是满同态。

命题3设M是有限表现右R-模，若M是Cn-平坦模, 则M是一个平坦预包的上核。

证明由于M是有限表现的, 则有正合列0→K→P→M→0, 其中P是有限生成投射模,K是有限生成模。下证K→P是平坦预包。

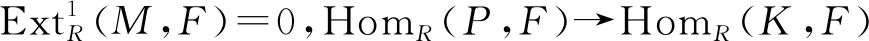
命题4设R是交换环,M是R-模，则:

①M是Cn-平坦模当且仅当对任何有限生成投射模P, 有P⊗RM是Cn-平坦模;

②M是Cn-内射模当且仅当对任何有限生成投射模P, 有HomR(P,M)是Cn-内射模。

证明①充分性: 取F=R即可。

必要性：由命题1, 对任何有限生成自由模F,F⊗RM是Cn-平坦模。设P是有限生成投射模, 则有自由模F及模Q, 使得F=P⨁Q。于是(P⊗RM)⨁(Q⊗RM)=F⊗RM是Cn-平坦模。由命题1,P⊗RM是Cn-平坦模。

②类似①的证明可得。

众所周知, 平坦模的纯子模及其对应的纯商模都是平坦模, 事实上, Cn-平坦模也有类似的性质。

定理2Cn-平坦模的纯子模与其对应的纯商模都是Cn-平坦模。

证明设F是Cn-平坦模,K是F的纯子模, 于是F+是Cn- 内射模, 且0→K→F→F/K→0是纯正合列。因此，0→(F/K)+→F+→K+→0是分裂的正合列,K+与(F/K)+都是Cn-内射模,K和F/K是Cn-平坦模。

2 Cn-平坦模是平坦模的充分条件

本节讨论Cn-平坦模是平坦模的条件, 并给出Cn-平坦模不是平坦模的反例。

设X是左R-模。文献[14]引入了X的n-余挠维数cndRX的概念, 即X的最短n-余挠分解的长度。文献[15]定理1.6证明了左R模N是内射模当且仅当N是Cn-内射模, 且cndRN≤1。

定理3对右R-模M, 以下各条等价：

①M是平坦模;②M是Cn-平坦模, 且cndRM+≤1;③M是Cn-平坦模, 且fdRM≤1。

证明①⟹②M显然是Cn-平坦模。由于M+还是内射模, 故有cndRM+=0<1。

②⟹①由于M是Cn-平坦模, 故M+是Cn-内射模。因为cndRM+≤1，由文献[15]定理1.6知M+是内射模，从而M是平坦模。

①⟹③显然。

Bass在文献[19]中引入了环R的左弱Finitistic维数：FFD(R)=sup{fdRM|fdRM<∞}。

定理4若FFD(R)≤n, 则对任何m≥n, CmF=CnF。

证明由m≥n及FFD(R)≤n, 得Fm=Fn，于是，Cm=(Fm)⊥=(Fn)⊥=Cn。因此，CmF=Cm=Cn=CnF。

推论1若w.gl.dim(R)≤n, 则对任何m≥n, CmF=CnF。

定理5对任何环R, C1F=CF=F。

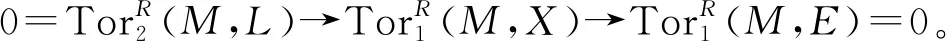
定理6设R是整环,M是无挠的C2-平坦模, 则M是平坦模。

上面2个定理说明n取0,1时，Cn-平坦模就是平坦模, 但当n取2时, 在一定的条件下也能证明C2-平坦模与平坦模的等价关系。接下来讨论Cn-平坦模的维数问题, 然后再借助其来找到Cn-平坦模(n≥2)与经典平坦模的差距。设L是R-模类，X是R-模，

…→Ln→Ln-1→·s→L1→L0→X→0

是正合列, 其中每个Li∈L，则该正合列称为X的L-分解。记Ki+1=ker(Li→Li-1),K1=ker (L0→X),K0=X。称Ki为X的第i次L合冲。当L分别是投射模类与平坦模时, 投射合冲与平坦合冲分别简称为合冲与弱合冲。

定理7设n是非负整数，对环R, 以下各条等价:

①w.gl.dim(R)≤n;

②任何n-余挠左R-模是内射模, 即Cn⊆I;

③对任何C∈C, fdRC≤n, 即C⊆Fn;

④对任何C∈C, idRC≤n, 即C⊆In;

⑦对任何L∈Cn, fdRL≤n, 即Cn⊆Fn;

⑧任何n-余挠左R-模是Cn-内射模, 即Cn⊆CnI;

⑨对任何M∈MR,M的第n次合冲是Cn-平坦模;

⑩对任何M∈MR,M的第n次弱合冲是Cn-平坦模。

证明①⟺②由文献[4]定理6.4即得。

①⟹③⟹⑥⟹⑤显然。

②⟹④设C是余挠左R-模。由文献[4]命题4.3(2),C的第n次内射上合冲是n-余挠模, 从而由假设是内射模，故有idRC≤n。

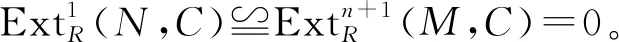
①⟺⑦⟺⑧见文献[15]定理2.2。

⑩⟹⑨显然。

推论2w.gl.dim(R)=sup{fdRC|C∈C}=sup{idRC|C∈C}。

一般地，要考虑一个环R的弱整体维数是需要考虑每个R-模的平坦维数的, 而上述推论则表明今后在讨论环的弱整体维数时只需考虑余挠模类的平坦维数或者内射维数即可。特别地, 当定理7中n分别取1与0时, 就可以得到关于Prüfer整环和von Neumann正则环的等价刻画。

推论3对整环R, 以下各条等价:

①R是Prüfer整环；

②1-余挠模是C1-内射模；

④对任何C,M∈C1及k≥1, 有ExtRk(C,M)=0；

⑥若c1dRX<∞, 则对任何M∈C1, 及任何k>0, 有ExtRk(X,M)=0；

⑦任何1-余挠左R-模的平坦维数不超过1 ,即C1⊆F1；

⑧任何1-余挠左R-模是内射模, 即C1=I；

⑨对任何C∈C, fdRC≤1, 即C⊆F1；

⑩对任何C∈C, idRC≤1, 即C⊆I1；

推论4对环R, 以下各条等价:

①R是von Neumann正则环；

②余挠左R-模是内射模, 即C⊆I；

③余挠左R-模是平坦模, 即C⊆F；

④n-余挠左R-模是平坦模, 即Cn⊆F；

⑤余挠左R-模是C-内射模, 即C⊆CI；

⑥余挠左R-模是Cn-内射模, 即C⊆CnI；

⑦纯内射左R-模是C-内射模；

⑧纯内射左R-模是Cn-内射模；

⑨右R-模都是Cn-平坦模, 即MR=CnF；

⑩有限表现右R-模都是Cn-平坦模, 即FP⊆CnF。

证明①⟺②⟺③⟹④显然。

④⟹①由I⊆Cn⊆F知R是IF环，由Cn⊆F⊆Fn知w.gl.dim(R)≤n。再由文献[14]命题4.3.2知弱整体维数有限的IF环就是von Neumann正则环, 故结论成立。

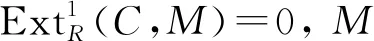
⑦⟹①设M是任何的右R-模, 则M+是纯内射模。由假设,M+是C-内射模。由定理1,M是C-平坦模, 即平坦模。

⑧⟹⑨同⑦⟹①。

④⟹⑥由Cn⊆F, 则F⊥=C⊆Cn⊥=CnI。

⑥⟹④由C⊆CnI, 则Cn⊆⊥CnI⊆⊥C=F。

③⟺⑤同④⟺⑥。

④⟺⑨⟹⑩显然。

⑩⟹④由FP⊆CnF即知F=FP⊇CnF⊇Cn成立。

由文献[2]推论4.3知每个右R-模都是余纯平坦模的环是左IF环。从上面推论可知每个右R-模是Cn-平坦模的环是von Neumann正则环, 即所有模都是平坦模的环。显然von Neumann正则环是IF环, 这就从维数的角度表明了余纯平坦模与Cn-平坦模之间存在着很大的区别。

下面继续讨论模类CnF的遗传性, 即Cn-平坦模的子模还是Cn-平坦模的情况。

推论5对环R, 以下各条等价:

①对任何L∈Cn, fdRL≤1, 即Cn⊆F1;

②1-余挠左R-模是Cn-内射模, 即C1⊆CnI;

③每个投射右R-模的子模是Cn-平坦模;

④每个平坦右R-模的子模是Cn-平坦模;

⑤每个Cn-平坦右R-模的子模是Cn-平坦模。

证明⑤⟹④⟺③⟺②⟺①显然。

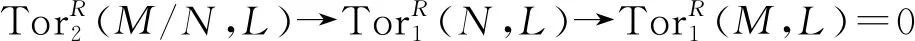
命题5若R满足推论5中任何一条, 则右R-模T是Cn-平坦模当且仅当对任何n-余挠左R-模L与i≥1, 都有ToriR(T,L)=0。

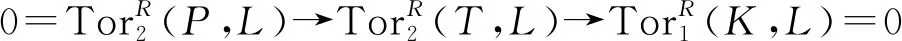
命题6设M是任意右R-模, 若对于任意C∈Cn,i≥1，都有ToriR(M,C)=0，则M是平坦模。

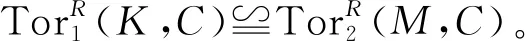
上述命题说明若在定义Cn-平坦模时有高阶的Tor函子等于零, 则Cn-平坦模就是经典的平坦模。根据前面的讨论可知, 当n≥2时, Cn-平坦模未必是平坦模，自然会问是否存在具体的例子，为此, 先给出一个引理(见文献[2]定理4.5)。

引理1设R是左凝聚环, 则每个余纯平坦右R-模是平坦模当且仅当R是左半遗传环。

例1由定理5, C-平坦模和C1-平坦模都是平坦模。现在来说明C2-平坦模未必是平坦模, 从而n≥2时, Cn-平坦模未必是平坦模。为此, 设R是左凝聚环, 并且w.gl.dim(R)=2。例如, 设V是赋值整环, 但不是域,R=V[x], 则w.gl.dim(V)=1,w.gl.dim(R)=2。由定理7, 2-余挠模是内射模, 故C2-平坦模是余纯平坦模。由引理1, 存在C2-平坦模不是平坦模。此外, 由定理1,M是C2-平坦模当且仅当M+是C2-内射模，这也说明了C2-内射左R-模未必是内射模。