齿轮螺旋线偏差比较测量结果的不确定度评定
运金芬 余 苏 邓水平
(1.二重(德阳)重型装备有限公司,四川618013;2.国家重大技术装备几何量计量站,四川610199)
齿轮螺旋线样板作为计量标准器具,它的螺旋线齿面是校准各种螺旋线仪器的标准,用于传递齿轮螺旋线参数量值、修正仪器示值、确定仪器示值误差。通过校准得到被检仪器修正值,在测量齿轮时,仪器应加修正值使用,以提高测量仪器的使用准确度。同时齿轮螺旋线测量仪器是基于齿轮螺旋线的展成原理,将被测齿轮的实际曲线与理论螺旋线的轨迹进行比较测量给出螺旋线偏差曲线的仪器。相关资料文献对其测量过程的分析,基本局限于最后计算结果表现出来的形式分析,评定过程比较简单,考虑的影响量较少,分析不全面不系统。本研究从齿轮螺旋线最基本的展成原理深入全面地分析测量过程的影响量,从而进一步提高齿轮测量仪器测量结果的可靠性,并为相关测量提供依据。
1 概述
以rb=24 mm、螺旋角β=14°、压力角α=15°螺旋线样板为标准,对WGT4000齿轮检查仪齿轮螺旋线倾斜偏差测量结果进行测量不确定度评定。
2 测量模型
螺旋角倾斜偏差在分度圆柱上测得,螺旋角实际值βs与设计值或标称值β0之差,以Δβ表示:
Δβ=βs-β0
(1)
用比较法测量螺旋线倾斜偏差时,
(2)
当分度圆螺旋线全部展开时为一直线,它是以圆柱正截面圆周长πd为底边,导程Pz为高的直角三角形的斜边长度,则螺旋角与导程的关系式为Pz=πdtanβ。则分度圆螺旋线在测量过程中展开时p为:
(3)
由公式(2),得出:
(4)
将公式(1)代入公式(4),得出:
(5)
由公式(3),得出:
βs=tan-1(rθp)
(6)
将公式(6)代入公式(5),最终得出:
(7)
式中,fHβ为螺旋线的倾斜偏差;β为螺旋角;p为螺旋线样板测量导程;r为螺旋线样板的分度圆半径;θ为螺旋线样板的展开角;Lβ为螺旋线样板的计值范围;Δβ为螺旋线样板的角度变化;β0为螺旋线的标准值;βs为螺旋线的测量值。
考虑各项影响因素,由公式(7)最终得出测量模型为:

δcw+δpx+Lβδwcδxc+δyb
(8)
3 灵敏系数
在公式(8)中,令Lβcos2β=K,灵敏系数ci=∂f∂xi,则:
式中,δcf为测量重复性;δtz为上下顶尖同轴度;δcw为测微系统示值误差;δpx为垂直滑架相对于上下顶尖的平行度;δwc为被校仪器与样板温度差;δxc为被校仪器与样板膨胀系数差;δyb为标准螺旋线样板引入测量不确定度。
当测量模型中的各分量独立无关时,则有:
展开为:
即:
4 标准不确定度
4.1 垂直导轨的直线性引入的不确定度分量u1
测量在分度圆上进行,垂直导轨的直线性引起分度圆半径变化。导轨的直线性取6 μm1000 mm,夹角φ=arctan(0.0061000)=0.0003°,服从均匀分布,按系数-psinφ投影,即该分量引入的不确定度分量为Lβ=80 mm,β=14°,所以K=85 mm。
经计算,θ=0.80 rad;p=80 mm;r=24.8 mm。
u(r)=u(φ)
=-80×1000×(3/10)×sin(0.0003°)
=-0.44 μm
u1=|c1u(r)|=0.80×0.44=0.35 μm
4.2 被校仪器转角θ引入的不确定度分量u2
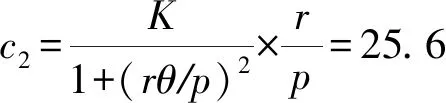
u2=c2u(θ)
=25.6×0.23×5×10-6×1000=0.03 μm
4.3 样板导程p引入的不确定度分量u3
被校仪器导程测量误差2.5 μm+L250 μm,均服从均匀分布,

u3=|c3|·u(p)=0.249×1.6 =0.40 μm
4.4 由测量重复性δcf引入的不确定度分量u4
对螺旋线偏差进行5次测量,按照极差法计算重复性,其测量数据如表1所示。

表1 重复性测量数据Table 1 Repeatability measurement data
s=(Δmax-Δmin)2.33=0.92.33=0.39 μm
u4=c4s=1×0.39=0.39 μm。
4.5 上下顶尖同轴度δtz引入的不确定度分量u5
用标准芯轴校准被校仪器的上下顶尖同轴度,经中测院校准标准芯轴同轴度为0.80 μm300 mm,轴系的工作角取30°,按正弦曲线最高峰计算,使用位置的同轴度区间半宽a=0.5×0.8×sin30°=0.2 μm,服从反正弦分布,则:
u5=c5·u(δtz)=85×0.14300=0.04 μm

表2 不确定度分量汇总一览表Table 2 Summary of uncertainty components
4.6 测微系统示值误差δcw引入的不确定度分量u6
测微系统示值误差用3等量块校准,在测微系统的测量范围内a=0.1 μm,k=2.58,则:
u(δcw)=ak=0.12.58=0.04 μm
u6=c6·u(δcw)=1×0.04=0.04 μm
4.7 垂直滑架相对于上下顶尖的平行度δpx引入的不确定度分量u7
u7=c7·u(δpx)=85×0.87300=0.24 μm。
4.8 被校仪器与样板温度差δwc引入的不确定度分量u8

u8=c8·u(δwc)
=80×1000×11.5×10-6×0.06=0.06 μm
4.9 被校仪器与样板膨胀系数差δxc引入的不确定度分量u9
螺旋线样板与被校仪器的膨胀系数均为(11.5±1)×10-6℃,校准实验室的温度在(20±2)℃范围内,样板与被校仪器的膨胀系数差半宽为±2×10-6℃,服从三角分布,则:
u9=c9u(δxc)=80×1000×2.0×0.82×10-6=0.13 μm
4.10 标准螺旋线样板δyb引入的不确定度分量u10
根据中国计量科学研究院的检定证书(证书编号CDjc2019-0544),二等螺旋线样板的不确定度U=1.2 μm,k=2,则:
u(δyb)=Uk=1.22=0.60 μm
u10=c10·u(δyb)=1×0.60=0.60 μm
4.11 合成标准不确定度计算
不确定度分量汇总见表2。

=1.0 μm
4.12 扩展标准不确定度计算
取k=2时,扩展不确定度为:
U=kuc=2.0×1.0=2.0 μm
当用rb=24 mm、螺旋角为14°的齿轮螺旋线样板进行齿轮螺旋线测量仪倾斜偏差测量结果的扩展不确定度U=2.0 μm。
5 结语
考虑了常规的影响量测量重复性、标准器与仪器的温差、标准器与仪器的线膨胀系数差、标准器示值引入的不确定度分量,并且对齿轮螺旋线样板在进行测量过程中,从展成测量的原理将被校仪器垂直导轨、仪器的转角、上下顶尖、测微系统、垂直滑架以及螺旋线样板的导程的所有影响量都进行了考虑,从而全面系统地确保齿轮测量仪器示值误差修正的准确可靠。其他参数的不确定度评定可参考不确定度评定过程进行。

