“问题链”：高中数学学习的“助力器”

王丽利

【摘 要】 高中是数学知识学习的重要拓展期，也是学生知识掌握的重要夯实期，借助问题链的设计则能够让学生的数学知识得以串联，并让学生的思维得到启发，帮助学生养成良好阅读习惯。本文就高中数学教学中问题链的设计进行探索，希望可以为高中数学教学的开展提供借鉴。

【关键词】 问题链  高中数学  数学学习

美国数学家哈尔斯曾说，解决一切问题的根本是数学，而问题则如同数学的心脏，带给数学强大动力。尤其在当前新教改不断深化的过程中，数学学习的开展也同样离不开问题的引导，只有让问题成为学生数学学习的重要“助力器”，才能让学生的大脑不断开动起来，才能让学生在思考的过程中实现知识点的连接，才能让问题成为学习的引导线贯穿于学习的整个过程之中，实现学生数学学习的深化。高中作为数学学习的重要时期，更加需要将问题思维引入到数学学习过程中来，让学生在学习的过程中生产问题、深化文化，让学生的数学学习形成发现、提出、分析和解决问题的不间断过程。

一、高中数学学习中问题链设计的重要性

1. 启发学生思考

数学知识的学习并不是简单的知识掌握，而是需要一边进行学习一边进行思考，通过思考了解数学知识的内在逻辑性，了解数学知识的紧密关系。问题链的设计不再是简单地让学生进行知识学习，而是让学生在思考中进行问题的回答，让学生在回答问题的过程中学习知识，这就让学生的头脑转动起来，带动学生思考习惯的养成，让学生能够将所学习的知识提高思考的方式实现内化。

2. 实现知识衔接

数学知识的学习并不是简单的单元式知识学习，而是每一节知识的学习都具有关联性和连接性，不同知识之间是紧密相连的，知识之间具有紧密的衔接性。通过问题链的设计则让学生将所学习串联起来，问题的回答也需要更多知识的联系和关联，这样学生想要回答问题则必然需要将知识联系起来，无形之中实现了知识的衔接，让学生的知识学习达到了更好的联系效果，也让学生达到了温故而知新的学习效应。

3. 提升教学质量

问题的提出和引导并不是随意进行的，其中融合了教师的教学开展理念，融入了教师对于知识点的教学思考，借助问题链的形式实现了更好的知识渗透和贯穿，实现了知识的教学的进一步推进。通过问题链的连接，教师与学生之间形成有效互动，教师也更加能够清晰地了解学生的学习情况，并结合学生的实际情况进行教学调整，这都让数学的教学质量得到提升，实现更好的教学效果。

二、高中数学学习中问题链设计原则

1. 目的性原则

教师在进行问题链设计时候要坚持目的性原则，以教学目的来引导学生进行思考，直捣教学任务的心脏。也就是说教师所提出的问题要服务于本节课的教学目的，从教学目的出发来进行问题设计，围绕教学难点来进行问题设计，则更加能够实现教学质量的提升，也能够让学生的问题回答与教学内容衔接起来。

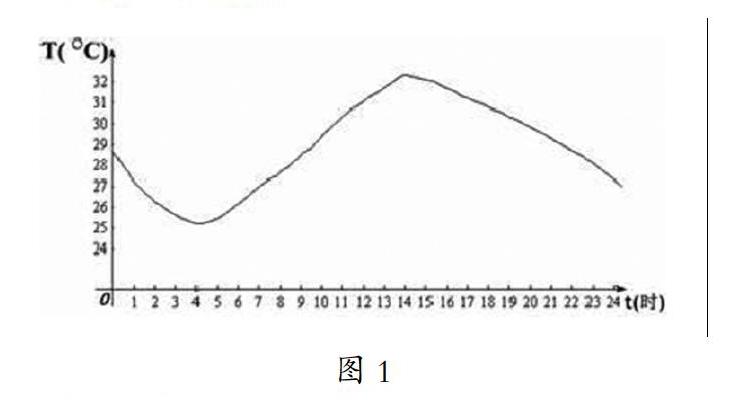
比如，笔者在“函数基本性质”教学过程中，则可以借助图形（如图1所示）来进行全天气温变化图像展示，题目为：下图是某地某日全天的气温变化图像：

结合进行目的来进行问题链设计：

（1） 同学们，通过此图可以看出气温是如何变化的吗？

（2） 大家是否可以使用数学语言来表达“随着时间的增大，气温随之升高”特征吗？

（3） 以区间[4，14]图像为例，从左到右从自变量与函数值变化的角度如何进行描述？

这样的问题链设计则更加能够帮助学生引入到教学内容之中，达到与教学目的的相符。

2. 启发性原则

问题链的设计并不是随意进行的，其根本目的便是对学生的数学学习予以启发，让学生在学习的过程中获得思想的引导，让学生自己来寻找问题的答案，通过自己的努力来探索知识，并对知识予以应用。因此，问题链的设计则需要秉持启发性原则。

比如，笔者在进行“二元一次方程”教学过程中，便在进行问题设计时候注重做好启发性的循序渐进，你如何来确定函数的零点位置？你如何缩小零点的所在区间呢？使用什么方法才能滿足精准度的要求呢？你可以总结你在二元一次方程中使用二分法求方程近似解的步骤吗？这样逐步引导的方式则让学生们能够逐渐掌握解题步骤，并对整个解题过程予以总结，在引导学生思考方面具有积极作用。

3. 适度性原则

数学问题链的设计并不是“越难越好”，也不是“越简单越好”，而是需要秉持适度性原则来进行问题链设计，寻找“最佳时机”来进行提问，将问题引入到学生的认知系统之中，避免简单问题链造成的“热闹假象”发生，让学生的思维无法得到更好锻炼，也避免过难问题链设计造成学生“百思不得其解”而让学生对问题望而却步。

比如，笔者了解有的教师在进行“函数的应用”教学过程中，为了让学生自己来进行三角函数诱导公式的推导，于是向学生提出问题：你了解单位圆的相关性质吗？可以借助单位圆的性质来进行三角函数诱导公式的推导吗？角β与角-β两角的终边交单位圆的交点有什么共同点？Sinβ与Sin（-β）相等吗？这样的问题均存在模糊性，且指向较为笼统，无法让学生很好地掌握其中知识点，难以提升学生的思维和智力水平。

4. 开放性原则

为了让学生的思维更具开阔性，让学生的思维能够达到发散的效果，教师在进行问题链设计的时候也需要坚持开放性原则，帮助学生养成多角度思考的习惯，让学生能够从更多层面认识问题、解决问题，从而帮助学生拓展学习思维的广度和深度，让学生能够真正积极有效地参与到课堂学习中来。

比如，笔者在进行“集合”教学过程中，便借助题目来让学生进行思考，题目为：已知集合，集合，那么请你想办法通过函数的概念构造从A到B的映射，并让集合B的每一个元素都能够在集合A中获得原象，并说一说所构造出的映射哪些是一一映射的，哪些是多对一映射的。这样的问题设置既让学生进行题目解答， 又达到了答案的不唯一，这都让学生的思维更加开阔。

三、高中数学学习中问题链设计策略

1. 概念问题链设计

概念是高中数学学习的重要基础，只有让学生对概念予以明晰，才能在数学题目解答中得以更好应用，实现知识的学习和掌握。教师也需要通过问题链的设计引导学生抽象概况出函数的具体概念并加深对其概念的理解，以此来达到概念的更好解析和渗透效果。

比如，笔者在进行“函数”教学过程中，便通过问题来对学生的知识学习进行引导：“同学们，我们之前已经学习了一些基本函数，那么同学们还可以列举出函数的类型吗？”此时同学们列举出了一次函数、正比例函数、二次函数等函数，之后笔者继续提问：“那么同学们有没有发现这些函数中的共性呢？你们怎么定义这些函数呢？”此时，笔者列举函数让学生判断：“y=1是函数吗？你们之前所学习的函数定义可以对其解释吗？”接着笔者又写出一些“特殊”的函数：，……再让同学们们进行分组讨论，不同函数间的对应关系有什么相同和不同之处，对应关系有什么特点，是否可以从集合的角度来进行函数概念的抽象分析，同学们是不是可以尝试使用集合与对应数学语言来进行对应关系的描述……这样的问题链设计让同学们从初中时候所学习的函数概念逐渐过渡到高中函数概念的掌握，对于数学概念之间的关系也有了更为深刻的理解。

2. 复习问题链设计

数学知识的学习不仅需要学习新知识，更加需要复习旧知识，并且很多时候新知识和旧知识之间要互相联系起来进行学习并让学生掌握，这样学生所学习的知识才更具有有效性。教师也需要在问题链设计时候注重新旧知识的结合，让学生达到新旧知识的全面巩固。

比如，笔者在进行教学过程中，进行知识引入，首先让同学了解函数图像是函数关系的直观表达，要想学习好函数则需要对函数三大变换方式予以复习巩固。知识巩固阶段笔者进行问题链设计：“基本初等函数图像如何进行作出呢？”这时候通过前面所学习知识的复习，同学们明白实际画图时候需要从函数解析式入手来进行定义域和值域的分析。

之后笔者继续提问：“画出函数，你们可以看出两个图像的关系吗？思考一下如何从第一个图像变换出第二个图像呢？”如果解析式为，那么有什么意义呢？这样循序渐进地进行问题引导，同学们不仅对之前所学习的知识进行了复习和巩固，也在此基础上学习到了新的知识，教师引入新知识的过程也更为顺畅，对于学生全面知识的掌握都具有重要影响。

3. 生活问题链设计

任何知识的学习最终目的则是要在生活中进行应用，只有让数学知识的学习与生活结合起来数学知识的学习才会更具意义。因此，教师在进行问题链设计时候也需要综合考量生活元素的融合，让生活元素在问题链设计中发挥作用，才能实现问题链设计的效果。

比如，笔者在数学教学过程中，有这样的一道例题：

一根长60cm的钢丝围成的矩形，长和宽分别是多少时候矩形的面积最大？

在进行此题目解答时候，笔者提出问题：“本题目中是否告知了矩形的长和宽？”同学们纷纷回答没有告知矩形的长和宽，之后笔者继续提问：“如果我们将矩形的长设为X cm，那么矩形的宽可以用X来表示吗？大家此时是否可以寻找到解答此问题的方法呢？”

以此例题为引，将此题目变形来引导同学们进行思考：

如果边长为60cm的正方形铁皮四个角切去四个相等的正方形后，沿着虚线折叠作成没有盖的合资，那么盒底长是多少时，盒子的容积最大？

此題目同样让学生们思考自变量X会受到什么值的影响呢？这时候建立起来的函数关系式是什么样的呢？还可以选取什么来作为自变量X？它的取值范围是什么样的呢？这样的问题思考不仅让同学们对题目予以解答，也让同学们了解到生活中数学应用的方式，让生活元素在数学知识的引导和学习中发挥作用，生活中数学的应用乐趣也逐渐为同学们所感受。

四、结束语

问题链的设计与原则应用能够更好实现教学质量的提升，能够让学生的非智力因素得以改善，真正实现教学效果的改善，达到更高教学质量的攀升。教师也需要从学生的实际情况出发，探索更好的问题链设计方式，让问题链的教学拓展学生的思维，让问题链的教学开展推动学生在数学领域获得更大进步与发展。

参考文献

[1] 季金斌.高中数学“问题链驱动”教与学的策略研究[J].数学大世界（小学五六年级版）， 2020（002）.

[2] 陈国明，郭靖.核心素养下高中数学问题链教学探究[J].新课程·下旬， 2019（8）.

[3] 陈国明.核心素养下高中数学问题链教学探究[J].新课程（下），2019（8）.

[4] 刘志利.高中数学课堂问题链的设计管窥[J].数学大世界（中旬）， 2019（1）.

[5] 巫斌.高中数学“问题链”设计的"四性"[J].数学教学通讯， 2019， 000（036）.

[6] 李应春.高中数学教学中“问题链”的设计[J].科教导刊（电子版），2019（13）.