基于机器学习的司法数据分析及建模研究——以“故意伤害罪”为例

戴非凡， 司卫云， 倪进平

(上海理工大学 光电信息与计算机工程学院, 上海 200093)

0 引 言

人工智能技术在司法领域的应用最早出现于上世纪70年代，美国法律界提出“电脑辅助法律研究”(Computer-assisted legal research)的构想，并依托硅谷等在数据挖掘、机器学习等人工智能方面的突出优势和大胆创新，首次设计并研发了“法律机器人”(Lex Machine)[1]。近年来，随着人工智能技术在国内的高速发展，中国法律科技市场也逐渐向人工智能与法律的结合上发展[2]。

中国传统司法界存在文献繁琐，法规众多，案件信息复杂，法官负担重，判案效率低等问题。其次，中国刑法采用相对确定的法制定刑，法官可在量刑幅度范围内行使自由裁量权[3]，从而难以避免同案裁量的差异性。因此，如何高效、准确、科学地设计一个公平公正的辅助量刑系统至关重要。运用恰当的机器学习算法进而构建专家模型是司法领域亟需解决的问题[4-5]。

然而，由于法律数据具有数量大、复杂化、多元化、速率快和不稳定等特点，导致基于机器学习算法的专家智能审判系统的建立尚处于起步阶段。并且在国内，就机器学习与司法大数据的跨学科研究多数仍处于仿真或理论分析阶段，缺乏较系统和成熟的技术支持。

因此，本文搭建了专家智能审判系统，初步实现了将多种机器学习算法用于司法判案，利用FCM、PCA、DNN和岭回归等多种算法，设计了一套完整的高精度刑期预测模型，以减轻法官工作负担，同时减少量刑过程中的主客观偏差和不公正现象。

1 专家智能审判系统模型设计

本文处理的数据来源于贵州法院，整理了从2016年1月至2017年5月所涉及的“故意伤害罪”案件，此类案件共5 000多宗。通过数据分析可知，法律案件的刑期判罚范围在0～240个月之间，跨度较大，若直接利用数据构造单一的回归模型会导致较大的刑期偏差。为了减小偏差，设计了如图1所示的模型框架。专家系统的建立和刑期预测主要包括数据预处理、数据挖掘和刑期预测三个阶段。研究可得阐释分述如下。

(1)数据预处理阶段：将采集的数据运用CRF序列标注模型和传统规则方法相结合的方式进行要素识别与提取；然后，清洗问题数据并对特殊文本进行类型转化。

(2)数据挖掘阶段：首先，利用模糊C均值聚类算法对预处理后的数据进行模糊分析，为分类模型提供科学有效的标签；然后，利用PCA主成分分析法对已提取的案件要素进行降维处理，减少计算复杂度；最后，利用深度神经网络对降维后的数据进行训练，实现案件的分类。

(3)刑期预测阶段：利用岭回归技术对各类案件进行建模分析，通过建立可靠的专家智能审判系统，进而达到对判罚刑期进行有效预测的目的。

图1 故意伤害罪判罚刑期预测流程

2 相关工作

2.1 模糊C均值算法

模糊C均值算法(Fuzzy C-Means Algorithm, FCM)是通过考查样本间的相互关系，分析隶属度，对类与类之间有交叉的数据集进行聚类[6]。通过引入隶属度因子m，将类内加权平均误差和目标函数推广到无限族，并给出交替优化(AO)算法，使得聚类结果更加客观真实地反映事实[7]。

考虑到分类模型的训练过程必须是一个监督学习的过程，因而，需要为每一个案件贴上模糊标签。而对于这类模糊数据，运用FCM算法将给样本提供较科学的类别标签。对此流程中各步骤可阐述如下。

Step1随机初始化模糊矩阵U，使每个样本j对c个类中的每个类i都有一个初始隶属度uij，并且满足下式约束：

(1)

Step2定义FCM的目标函数为：

(2)

其中，ci为每类的聚类中心，xj为样本，m为隶属度因子。

Step3将带有等式约束(1)的目标函数采用拉格朗日乘数法进行转化得到：

(3)

Step4分别对式(3)变量uij和ci求导，令导数为零，进而得到聚类中心ci和隶属度矩阵uij的迭代公式为：

(4)

(5)

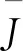
Step6若迭代次数大于最大迭代数，则算法停止。

2.2 深度神经网络算法

本文利用深度神经网络(Deep Neural Network，DNN)实现对贵州法院故意伤害罪案件的分类，进而构建一个高精度的故意伤害罪的案件分类器。总地来说，首先运用词袋模型(Bag of Words)[8]，将法律案件中各要素的文本信息转化为计算机可理解的数据形式[9]；然后使用主成分分析算法(Principal Component Analysis，PCA)[10]，在保证准确度的同时，降低特征维度并提高模型构建效率[11]；最后实现DNN模型的构造。

典型的深度学习模型(Deep Learning)，是机器学习算法中一个重要的分支[12]。神经网络中最基本的单元为神经元[13]，研究给出的模型结构如图2所示，其输入与输出关系可表示为：

(6)

其中，ai表示第i个神经元的输入；wi表示对应第i个神经元的连接权重；θ表示神经元阈值；f表示激活函数；y表示神经元的输出。

将如上结构的多个神经元按照一定的层次结构连接起来，就得到了神经网络，主要是由输入层、隐藏层、输出层组成。DNN就可以认为是有很多隐藏层的神经网络，如图3所示。神经网络隐藏层的层数可以依照数据的复杂程度合理增减，以此提高模型的表达能力，但模型的复杂度也会随着隐藏层层数的增加而增加。

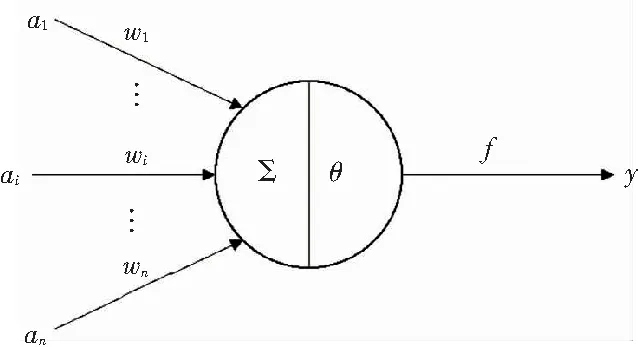
图2 神经元模型

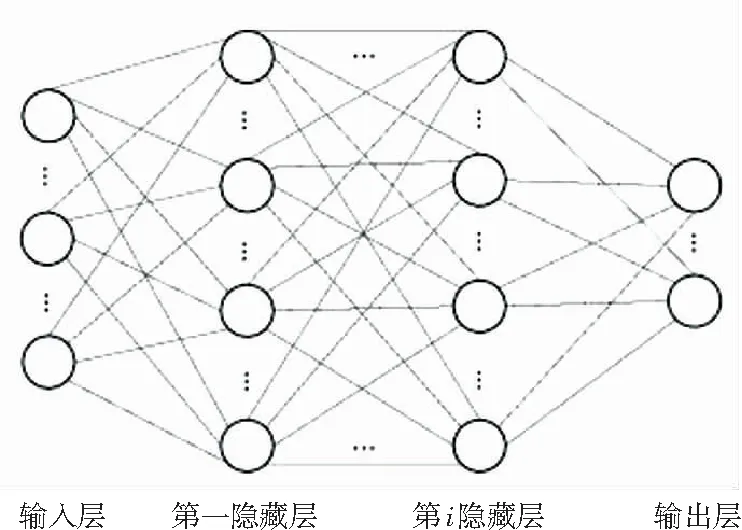
图3深度神经网络结构图

2.3岭回归算法

较常用且易于实现的线性回归在处理例如本文的较高维数据时常会出现多重共线性问题、求逆运算不稳定、模型解释性较差、预测准确性较低等问题[14-16]。

分析可知，岭回归算法[17]是针对共线性数据分析的有偏估计的一种回归方法，通过牺牲解的无偏性，以丢失部分信息、降低精度为代价获得更加准确的预测结果。同时因为引入了惩罚项，有效防止过拟合，提高模型的泛化性能[18]。岭回归目标函数为：

(7)

其中，λ为正则化系数。将上式两端对W求导，得到最优解W*为：

W*=(XTX+λI)-1XTy.

(8)

针对同样呈现高维特性的故意伤害罪数据，本文依据各案件的犯案要素，对每一类样本基于该算法建立一种回归分析模型来预测该类作案人员的刑期。

3 实验结果及分析

3.1数据预处理

不同于普通的语料库数据，贵州法院故意伤害罪案件数据以虚拟编号的形式存储，其字典示例见表1。为了让计算机能够理解这类数据，采用了词袋模型对数据进行有效编码，其结果见表2，得到一个5 348×78的特征矩阵。表2中列表示案件要素，1表示该案件中存在该要素，0表示不存在。词袋模型完成了对原始故意伤害罪案件文本要素到文本向量空间的映射。

表1 故意伤害罪案件要素字典示例

Tab. 1 Example of a dictionary of elements of intentional injury crimes

ID案件要素集12345︙{102,101,102001,201,106001,…,202,201001,106,202004,101001}{102,101,201,106001,…,102005,201001,106,202004,101001,102005}{102,101,201,106001003,…,106,101001,104,102001,104004,106001}{102,101,201,106001003,202,…,101001,104,102001,104004,202002}{102,101,201,202,201002,106,…,104,102001,104004,106001,202004}……

3.2 基于FCM算法的故意伤害罪聚类结果分析

本文将Xie-Beni (XB) 作为度量FCM聚类方法优劣的评价指标，其表达式为：

(9)

式(9)表明，当实现目标函数极小化，同时满足类间距离极大化，即不同类之间的样本分散较开时，聚类效果较好。

表2 故意伤害罪词袋模型示例

实验中，分别运用K-Means和FCM对预处理后的故意伤害罪案件的刑期进行聚类，并将2种算法的聚类结果进行了对比。在K-Means聚类实验中，设置最大迭代次数为1 000次，类别个数k为5；在FCM聚类实验中，设置最大迭代次数为100次，类别个数c为5，模糊(隶属度)加权指数m依据经验值取为2.0，XB为0.0565，效果如图4所示，其中横、纵坐标均表示刑期(月数)，红色×表示FCM各类聚类中心，5种不同的颜色代表不同的类别。其中，表3是K-Means和FCM刑期聚类分布的平均偏差。由表3易见，对于法律数据，FCM聚类比K-Means聚类有更好的聚类效果，能够为分类器提供更可靠的类别标签。

图4 FCM聚类效果图

表3 故意伤害罪案件聚类分布对比表

Tab. 3 Comparison table of cluster distribution of intentional injury crime cases

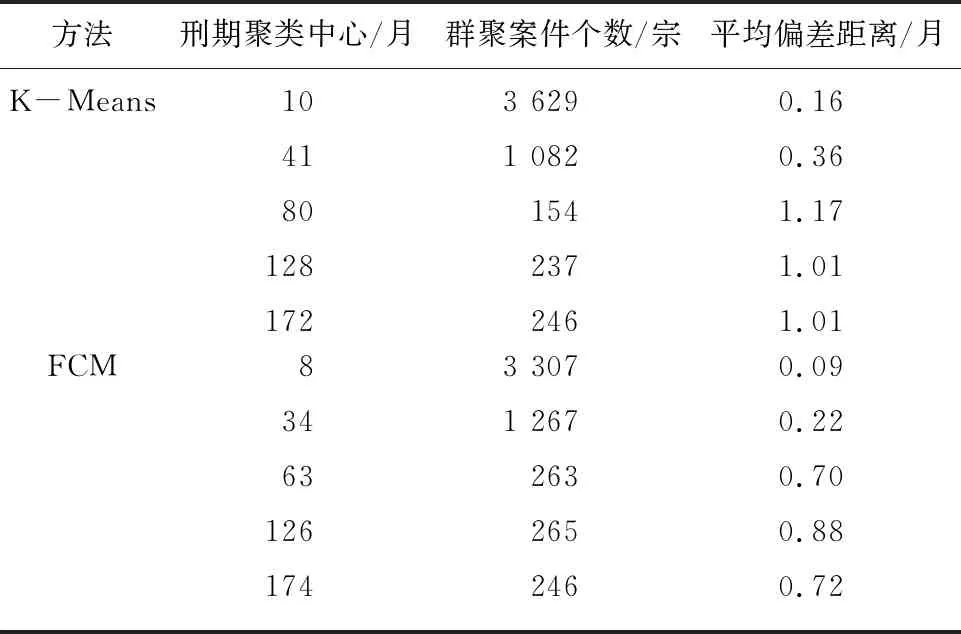
方法刑期聚类中心/月群聚案件个数/宗平均偏差距离/月K-Means1041801281723 6291 0821542372460.160.361.171.011.01FCM834631261743 3071 2672632652460.090.220.700.880.72

3.3 基于DNN算法的故意伤害罪分类结果分析

(1)PCA结果分析。经统计，贵州法院故意伤害罪案件数据共有不重复要素(属性)78个，研究将3.2节中的词袋模型输出作为PCA主成分分析的输入，提取原始数据的85%主成分，即将78维的特征空间投影到35维的特征空间下，在保证数据特性的同时实现维数的约减，大大减少了计算开销，使得数据更易使用，同时也能在一定程度上去除数据噪声。

(2)DNN结果分析。本文提出的DNN分类器模型是基于TensorFlow深度学习框架构建的。具体实现过程可阐释如下。

首先，在DNN分类器训练前，将聚类得到的结果作为5 348个案件的真实类别标签，将这些带有标签的数据作为DNN分类器训练的原始数据，并基于交叉验证法随机提取80%的数据量(4 278)作为DNN分类器模型的训练集，剩余的20%(1 070)作为测试集用于模型评估。

其次，分别对比实验了3层、4层、5层DNN模型后，最终选择5层神经网络模型为本文的DNN分类器，具体网络结构见表4。其中，使用Relu()函数作为隐藏层的激活函数；使用Softmax()函数作为输出层的激活函数；运用Momentum算法作为反向传播的优化器，使其收敛速度更快，震荡更小。

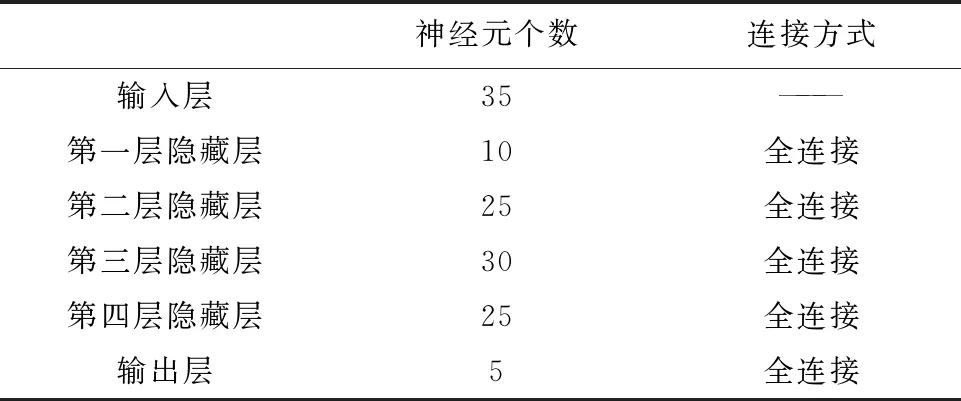
表4 DNN网络结构

在实验阶段，为了突出DNN算法的有效性和优越性，本文将其与经典的SVM分类算法进行了比较，结果见表5。分析可知，基于DNN算法的分类模型比基于SVM算法的分类模型具有更高的分类精度，能给案件提供更精准的预判。最后统计分类结果中属于各类的案件刑期的分布情况见表6，例如，分类结果属于第一类的案件中，绝大部分案件的真实刑期分布在144～240个月之间。通过明确刑期分布区间，可为后续的建模分析奠定基础。

表5 SVM与DNN分类算法效果对比图

表6 各类案件刑期分布

3.4 基于岭回归模型的故意伤害罪判罚刑期预测结果分析

将训练集依据FCM的结果分为5组不同类的案件。其中，属于第一类的案件有280宗，属于第二类的案件有233宗，属于第三类的案件有237宗，属于第四类的案件有1 308宗，属于第五类的案件有3 290宗，并分别对这5组数据构建回归预测模型。基于式(8)求得的模型参数W*值可得多元线性回归预测模型：

(10)

(11)

根据每一类的回归模型，对测试集案例进行刑期预测，λ取为e-10，可以得到每一类案件的刑期预测模型见表7。

表7 各类案件刑期预测模型

将测试集分别输入到对应类别的回归模型中得到每个案件的刑期预测值，并与实际值进行比较，得到平均绝对值误差(MAE)，结果如图5～图9所示。其中，每幅子图的横坐标表示属于该类的案件个数，纵坐标表示每个案件对应的刑期(月数)；圆形点(蓝色)表示每个案件的实际刑期，三角形点(红色)表示每个案件的预测刑期。从图5～图9可以看出，整体案件的预测刑期与真实刑期大致接近。

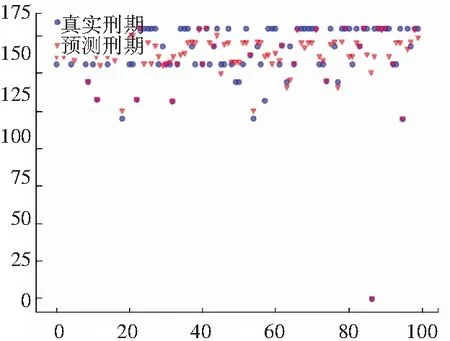
图5 第一类案件刑期预测结果

图6 第二类案件刑期预测结果

图7 第三类案件刑期预测结果

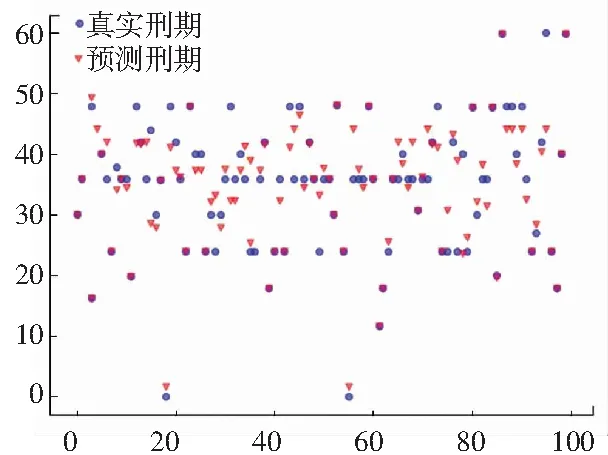
图8 第四类案件刑期预测结果

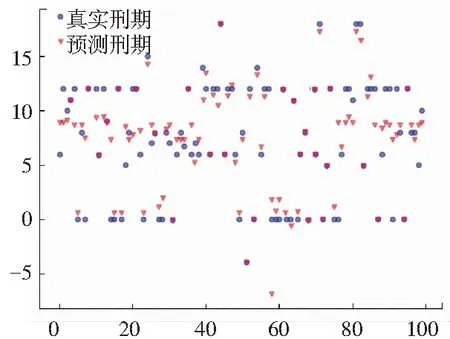
图9 第五类案件刑期预测结果

最后，通过对比了岭回归(Ridge)、Lasso回归、线性回归(LR)、前向逐步回归(FSR)这几种较常用的经典回归预测算法的MAE，结果如图10所示，明显发现岭回归算法更适用于本文设计的基于故意伤害罪司法数据的专家智能审判系统预测模型的构建。

图10 各预测模型预测刑期偏差对比图

Fig. 10 Comparison of predictive models for predicting sentence deviation

4 结束语

本文结合几种典型的机器学习算法，如模糊C均值聚类算法、主成分分析技术、深度神经网络和岭回归算法等，针对贵州法院故意伤害罪案例数据，设计并构建专家智能审判系统，进而对判罚刑期做出精准预测，为辅助判案提供理论依据。并利用真实案例加以验证，得出本文搭建的模型能够以较小的偏差对判案刑期进行有效预测，为司法工作注入前所未有的创造力。下一步，将针对样本分布不均匀等问题，在数据处理和算法上进一步改进，构建预测精度更高的专家系统模型。