基于空间光调制器的层析成像技术

刘洪顺，王 喆，胡 琪，孙家成，邓家春

(天津理工大学 理学院，天津 300384)

1 引 言

在重现真实物理世界的光波场信息方面，先后出现了平面照相与显示成像技术和3D立体成像显示技术[1]。现如今3D技术多种多样，如市面上流行的利用人的双眼视差法制作的偏光镜和利用两束相干光在特制的化学材料上记录与再现物体光波信息的全息术[2-4]。然而偏光镜的缺点是使用时会令人产生眩晕和视觉疲劳，而相干法全息术的实现条件非常苛刻，抗干扰性差，难以实现彩色和非相干光显示成像。目前，具有较大发展前景的是通过全息再现方式实现裸眼3D技术的全息成像技术[3]。这种技术可以利用空间光调制器(Spatial Light Modulator,SLM)[5]良好的相位复原特性来实现[6-9]。韩国大学的Hwi Kim等人[10]提出利用两台空间光调制器(振幅型和相位型各一台)，实现物光波前重现的全息技术。该技术使用计算机模拟出一个平面物光场，然后用第一个振幅型SLM加载光场强度信息，再利用第二台相位型SLM加载相位信息，从而重现了模拟计算的物光光场。而后通过成像透镜和CCD形成的成像系统对物光光场进行探测。他们通过改变观察视角分析了平面物光的立体全息性质。但该研究仅停留在利用计算模拟物光光场的阶段。与此同时，其重现的光场对于成像系统直接观察具有较好的虚拟现实效果，但还不能通过漫反射体(如幕布)反射后被人眼观看。

上述难点有两部分原因：

(1)对于真实场景的物光波前进行定量采集需要特殊的光学仪器；

(2)漫反射体会严重改变入射光场，使得物光失去原有的波前分布(就好像人们无法像使用镜子一样，用人眼从墙面直接看到物体的像一样)。

随着科学技术的进步，人们已经可以通过波前传感器(Wave Front Sensor,WFS)对实物光场实现定量采集[11]。而计算全息与WFS的结合[11-12]，使得解决上述两个难点成为可能。本文采用WFS定量采集真实物体的波前信息，然后利用两台SLM复合调制实现物光波前重现。同时，本文利用计算全息技术，将光学系统的传递函数与物光波前进行卷积运算[13-15]，获得了物光经过光学系统后的光场。本文通过模拟成像透镜，设计了光学系统，通过加载它的传递函数，重现出了物光光场经过透镜后的表面波前效果。因此，在对物体进行全息成像探测时，只需利用CCD观察实验成像结果，而不需要使用真实的透镜，从而减少了实际成像系统引入的诸如色差、球差等像差效应[16]。

通过灵活调整透镜参数，并结合基于单次傅立叶变换的分段衍射算法[17]，本文根据CCD成像面元尺寸和成像面位置的需要，设计了与之相匹配的透镜参数，以获得理想的放大率和分辨率。该技术还可根据探测需要，用计算全息方法灵活更换探测方式(如光谱成像、特种显示技术等)，该技术可在生物医学、卫星探测等领域得到广泛应用。这项研究把计算全息和实验全息结合起来，受实验环境影响较小，灵活性较大，前景广阔，有望成为3D全息显示技术的一个重要发展方向。

2 衍射理论算法

从已知空间平面经后续介质传播至任意观察位置上的光波复振幅表达式可通过惠更斯-菲涅耳原理来计算[18-20]。

菲涅耳衍射坐标示意图如图1所示，可见，光经自由空间传播距离d后在x-y衍射平面上p点处的光场U(p)是x0-y0平面上面元dS内发出的所有光波复振幅U0(x0,y0)在衍射面p点处的相干叠加。所以p点的合振动等于整个S面上各点传播到x-y平面上p点处光振动的积分：

U(p)exp(i2πvt)=

(1)

式中，k(φ)为并未作严格定义的倾斜因子，v为光波的频率[17]。

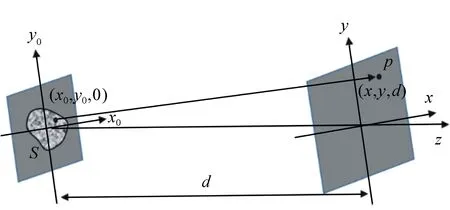
图1 菲涅耳衍射坐标示意图 Fig.1 Fresnel diffraction coordinate diagram

根据标量衍射理论，在傍轴近似的情况下[18,19]菲涅耳衍射积分可变为：

(2)

式中，k=2π/λz，λz为光波长λ沿z轴方向的分量，λ为光的波长。

将式(2)展开，并把与积分无关的x2和y2项提到积分号外，可得：

(3)

(4)

公式(4)称为“单次快速傅里叶变换算法”(Single Fast Fourier Transform Algorithm，S-FFT)[21-22]。由于该算法仅使用单次快速傅立叶变换，所以其计算速度较快，失真率较低[21]。

3 衍射受限透镜成像系统

运用S-FFT算法结合透镜的相位变换作用，就可以模拟出光波通过透镜成像系统后得到的光波复振幅信息，从而可以对物光光场进行成像研究。

已知光波在透镜后表面的光波复振幅可通过透镜的相位变换因子t(x,y)计算。

图2 透镜的相位变换作用示意图 Fig.2 Schematic diagram of lens phase shift transformation

如图2所示，设对称透镜的焦距为f,物距为p，像距为q。在傍轴近似的情况下，点光源S产生的发散球面波在透镜前表面P1上的复振幅为：

(5)

在傍轴近似情况下，忽略透镜的吸收，通过透镜后的汇聚球面波会在像点S′处交为一点。因此其在透镜后表面P2上的复振幅分布应为：

(6)

引入复振幅透过率函数t(x,y)来表达透镜的变换作用：

(7)

所以复振幅透过率函数可表示为：

(8)

再由透镜的成像公式：

(9)

可将式(8)改写为：

(10)

考虑无像差薄透镜的孔径尺寸有限，用P(x,y)表示孔径函数(或光瞳函数)，其可定义为[18]：

(11)

于是无像差的透镜相位变换因子为：

(12)

因此，物光传播距离d，经过透镜后，表面的光场复振幅为：

(13)

其中，U1(x,y)为式(4)通过S-FFT算法获得的自由空间传播后的光场。

4 强度-相位复合调制的SLM波前再现成像

实验中将两片相距为25 mm的金属片错位摆放。片上分别镂空刻有英文字母“F”和“L”，如图3所示。这样在光照下，就构建了一个简单的立体物，它在两个不同视觉深度平面上形成了不同的清晰像，而且其包含着其他平面上物光光场的衍射光场，“F”尺寸为0.7 mm×2.6 mm,“L”尺寸0.6 mm×2.0 mm。

图3 字母“F”和“L”组成的立体物 Fig.3 A 3-D structure composed by letters “F” and “L”

实验中首先使用物光波前采集设备采集波前的数据信息，所用的为美国Thorlabs公司生产的WFS300-14AR型波前传感器，微透镜阵列的面元个数为17×13，利用该设备可对立体物的物光波前信息进行定量采集，包括强度信息和相位信息，如图4所示。入射均匀光(波长为532 nm，功率为100 mW)照射到两个平面金属片上，经过镂空的字母“F”和“L”，透射出的衍射光场变成畸变的波前。两个畸变的物光光场再经过一段衍射距离后(该距离为第二块金属片“L”到WFS间的距离，为125 mm，图4)被WFS收集，采集到其波前数据信息。

图4 波前信息采集示意图 Fig.4 Schematic of wavefront information acquisition

用WFS采集该物体的波阵面分布图，如图5所示。由于波前传感器采集的相位精度较高，其空间像素数量并不多，仅有17×13。因此需要对采集到的波前数据进行插值，本文运用线性插值算法[23]将数据扩展为170×128。

图5 WFS波前信息采集数据图 Fig.5 Acquisition data map of WFS wavefront information

后面实验用到的强度灰度图是由波前采集到的物光强度数据制成的，如图6所示。相位灰度图则是根据WFS采集的相位数据，由公式(13)用S-FFT算法计算物光场到达焦距为150 mm的透镜后表面的相位项得到(如图7所示)。

图6 含有物光波前信息的强度灰度图 Fig.6 Intensity grayscale image containing object wavefront information

图4中物1“F”到WFS的距离为150 mm，两物的距离为25 mm，入射光波长为λ=532 nm，透镜焦距为f=150 mm。通过计算原物光波场到达透镜后表面的复振幅，得到其相位分布信息，制作成相位灰度图，如图7所示。

图7 d1=150 mm处透镜后表面光场相位分布灰度图 Fig.7 Phase distribution gray image on the back surface of the lens at d1=150 mm

接着，利用得到的光场强度和相位分布生成强度灰度图和相位灰度图，并将这两项分别加载到两台SLM(如图8所示)的芯片上进行光波调制，从而实现波前重现。实验中采用的是德国HOLOEYE公司的纯相位型的空间光调制器(PLUTO-NIR-011)，有效面元尺寸为15.36 mm×8.64 mm。其中，强度调制是通过一个相位型SLM与一个偏振分光棱镜(Polarizing Beam Splitter,PBS)实现的[24]，相位调制使用了另一个空间光调制器。其空间分辨率为1 920 pixel×1 080 pixel，计算时运用了分段衍射算法[17]来灵活调节强度图和相位图的画幅尺寸和空间分辨率。

图8 SLM强度-相位复合调制的波前再现成像示意图 Fig.8 Schematic diagram of wavefront reproduction imaging of SLM intensity-phase composite modulation

经过强度图和相位图复合调制后，激光器出射的均匀平行光形成原物光通过透镜后的波前光场分布，在空间中形成了该物体的波前重现全息层析像。

图9 现有SLM全息术实验效果的示意图 Fig.9 Schematic diagram of experimental results by existing SLM holography

由于实验中已经加入了成像透镜的相位变换因子，用CCD直接在像面上探测即可观察到物体的像。通过调节虚拟透镜的物距或CCD与SLM之间的像距，即可看到物体不同深度平面的清晰像(如图9所示)。

最终通过CCD采集得到的图像如图10所示。该结果表明，光场经SLM调制后在像空间形成了三维物体的立体全息像，且不同深度下离像光场发散剧烈，轴向分辨率较高。

图10 层析成像实验结果 Fig.10 Tomography experiment results

对于图10的实验结果，将从以下几个方面加以分析：

(1)计算成像的纵向拉伸度

“F”和“L”的物距之差为25 mm，而根据透镜的成像公式计算出的“F”和“L”的理论像距分别为VF=300.0 mm和VL=340.0 mm，像距之差为40.0 mm，而实验测得的像距之差为39.1 mm，立体物整体纵向拉伸度的理论值和实验值分别约为1.6和1.156 4，相对误差为2.25%。实验与理论符合较好。

需要说明的是，因为像距与物距的变化关系并非线性关系，因此理论上立体物在纵向上的像点间距会产生畸变。技术上是可以通过组合透镜来消除这种纵向畸变的，但由于这项研究并非本文重点研究内容，实验中并未做过多说明。

(2)计算全息像的横向放大率

利用成像公式理论计算出的字母“F”的横向放大率βF=VF/UF=1，字母“L”的横向放大率βL=VL/UL=1.2，两者的放大率比值约为0.83。这个比值可以反映立体物在不同深度像面处产生的横向畸变，也就是说一个立方体在空间中所成的立体像本身就存在畸变，像距越大，横向放大率也越大。

实验中，首先测量了WFS采集到的物光强度占总画幅的比例，如表1所示。其中，“F”的水平(x轴)和竖直(y轴)方向比例分别为35%和86%；“L”在两个方向上的比例分别为32%和72%。接着，将比例值分别乘以WFS的真实面元尺寸(5.95 mm×4.76 mm)，得到采集的物光空间中“F”和“L”的尺寸分别为2.09 mm×4.11 mm和1.90 mm×3.40 mm。

表1 WFS采集到的光强分布比例

然后，利用SLM和WFS的有效面元以及像素之比得到两仪器之间的空间换算放大率，如表2所示，x、y轴方向分别为322∶1和182∶1。接下来，用金属片上“F”和“L”实际物的尺寸(分别为0.7 mm×2.6 mm和0.6 mm×2.0 mm)分别乘以空间换算放大率，得到实验中前后两物的大小分别为2.25 mm×4.73 mm和1.93 mm×4.19 mm。

表2 SLM实验中的重现物尺寸

通过测量得知，CCD采集到的“F”和“L”的像面图案在x轴、y轴上占画幅的比例分别为(29%，75%)和(30%，67%)。将上述比例乘以CCD的面元尺寸(8.5 mm×6.8 mm)，就得到了实验中“F”和“L”像的尺寸，分别为2.49 mm×5.11 mm和2.59 mm×4.58 mm。最后，将实验中的像尺寸除以物尺寸，即可得到全息层析成像后“F”和“L”在x轴、y轴方向上的横向放大率，分别为(110%，108%)和(134%，109%)，其相对误差分别为(10.6%，8%)和(11.7%，9%)。实验的相对误差较小，实验结果与理论值较符合。

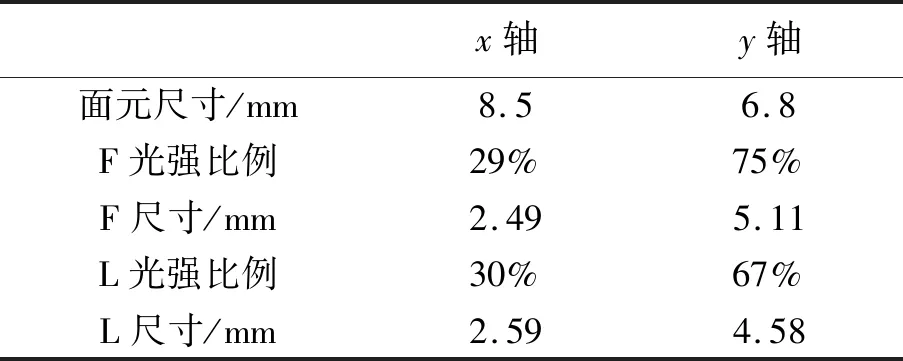
表3 CCD采集的像尺寸及其计算参数

(3)计算全息成像后的角扩散度分布

根据实验中“F”和“L”的离像面图像，可获得角扩散度，也就是像点发散光的发散角。理论上这个发散角同样与像距相关，其与像距的关系如图11中实线所示。由于实验中仅对两个面进行成像，所以仅分析“F”和“L”所在像面处角扩散度的实验值(图11中“*”号数据点)。其分析过程如下：

实验中所用设备SLM的有效面元尺寸为15.36 mm×8.64 mm，CCD的有效面元尺寸为8.5 mm×6.8 mm。在(1)中测量了两个字母在清晰像位置的横向宽度，所以这里仍然取横向宽度作为参考。通过实际设备的面元尺寸可计算得到“F”和“L”在两成像面位置的尺寸宽度(下面仅以x轴方向为例)：

而根据SLM的面元尺寸计算可得，tanθ=15.36/q，q为像距，得到在x轴方向上“F”和“L”处的角扩散度理论值分别为2.95°和2.61°，其曲线分布如图11所示。

图11 角扩散度随像距变化图 Fig.11 Angular spread varies with image distance

可以看到理论值与实验值的角扩散度差距较小，相对误差分别为2.6%和0.7%，实验结果基本符合理论预期。其误差主要来自两个方面：

(1)空间光调制器的相位调制精度、反射面元的平整度及其光滑程度。实验中不够光滑的镜面反射可能带来散射效应，而相位上的微扰动足以改变成像质量。

(2)对于模糊像的散斑宽度的测量会因测试者不同而有差别。实验中首先将两个图像归一化并平方后相减得到方差图，再通过原位多次测量取平均的方法消除随机误差(随机误差主要是由CCD的暗噪声和光源的稳定性差产生的)。然后再提取出清晰像边界以外的光强分布曲线，选择曲线最大值的1/e为边界测量到的宽度。

5 计算全息仿真成像

为了进一步说明实验原理和这项技术的有效性，采用第三章的衍射受限系统，模拟出通过WFS采集到的层析物体字母“F”和“L”，利用其强度信息和相位信息复原出其通过虚拟透镜后的层析成像结果，如图12所示。

图12 仿真成像实验结果 Fig.12 Simulation results

由图12可以看出，清晰像有一定程度的虚化，这与靠近光源物的物光经过远离光源物后的衍射效应有关，是由一些高空间频率的物光发生了遮挡和衍射效应导致的。同时(以图12(b)为例)，远离光源物(“L”)的清晰像也会受到影响，因为照射在远离光源物(“L”)的光场中存在一部分靠近光源物(“F”)的物光，而这部分光线已经带有靠近光源物(“F”)的光场信息。所以在三维立体成像或者多层平面物体成像中，图像清晰度会受到三维物体结构的影响。利用该衍射算法计算出的成像结果与SLM实验观察到的图10的层析实验结果比较符合。

6 结 论

本文利用波前传感器对实物光场进行了定量采集，并利用分段衍射算法对光场衍射及其经过成像系统后的衍射光场进行了理论计算。在此基础上，通过两个空间光调制器在实验上实现了物光波场及其透镜后表面光场的波前重现，并形成了空间立体的全息层析像。

通过对成像数据的定量分析可知，在物光衍射距离为150 mm的情况下，在298.5 mm和337.6 mm处可以分别得到“F”和“L”的清晰的全息层析像。立体物前后不同深度在两个成像面x、y方向上的横向放大率分别为(1.1，1.08)和(1.34，1.09)，与透镜成像公式计算得到的横向放大率(1，1.2)相比，相对误差为(10.6%，8%)和(11.7%，8%)。角扩散度分别为2.95°和2.61°，其相对误差分别为2.6%和0.7%。实验结果与理论值较符合。

分段衍射算法是波前重现技术中的一项关键技术，它有效改善了S-FFT算法在模拟衍射中画幅尺寸和图像分辨率，使图像失真度大幅下降。此外，可知用计算全息方法对波前经光学系统衍射后的光场进行模拟计算是可行的，该方法可进一步扩展，以解决真实光学系统难以满足光学探测需要的问题，在光谱分辨成像、时域分辨光谱成像、零梯形校正成像等领域发挥重要作用。该研究成果是上述问题得以实现的关键前提和重要基础，且可在生物医学成像、卫星探测等领域得到广泛应用，具有较高的使用价值和发展空间。