超电大尺寸海面电磁散射计算的混合面元法研究
刘旭波,杨润秋,齐聪慧,杨 伟
(1.中国人民解放军91977部队,北京 102249;2.电子科技大学 电子科学与工程学院,四川 成都 611731)
0 引言
随着高精度雷达在海洋军事领域的应用,海面电磁散射的研究越来越受到重视[1-2]。超电大尺寸的海面电磁散射仍是海面微波遥感的重点难点问题。一方面,适用于海面电磁散射计算的解析方法如基尔霍夫近似算法、微扰法、双尺度算法和小斜率近似等[3-4],只能应用于较为平静海面的计算中,适用范围受到了限制;另一方面,计算电磁学中的数值算法如矩量法、时域有限差分法和有限元法[5]等,以及这些算法的改进算法,如多阶矩感应方法(MOMI)、边界积分方程法和前后迭代物理光学方法(FBIPO)[5-8]等有着很高的计算精度,还有采用多种方法结合的混合方法,如MoM和IPO混合方法、MoM和几何绕射理论结合方法等[8-9],但对于超电大尺寸的海面电磁散射来说,计算量非常大,计算机资源和计算时间消耗巨大,单一的数值计算方法在海面电磁散射和海杂波研究中并不适用[3]。因此,发展一种使用范围广、精度高、计算速度快的海面电磁散射回波近似方法一直是海面散射研究的重点难点问题。2012年,张民提出了一个基于场的半确定性海面电磁散射模型(FBSDM)[10],该模型对局部散射起主导贡献的小尺度海浪散射场用解析方式推导,避免了对海面的精细剖分,极大减小了电大海面场景电磁仿真需要的计算资源和计算耗时。2015年,陈锟山提出基于AIEM算法对海面电磁散射计算方法[11]。2016年,郭立新提出基于双尺度海面模型的思想,利用半确定性面元散射模型结合弹跳射线法对海面散射进行计算[12]。但这些方法只适用于具有单一特征的海面,对于含有卷浪海面,这些算法不能同时兼顾卷浪计算的精度和整体海面电磁散射的速度。
为快速高效地实现超电大尺寸的海面电磁散射计算以及动态三维海面的海杂波快速仿真,提出一种基于散射中心理论的海面面元混合电磁散射计算方法。该方法基于海面电磁散射的双尺度模型,将海面看成不同尺度海面。对于大尺度海面采用海面几何模型生成方法来模拟海面轮廓,采用文氏谱通过线性滤波法来生成大尺度的海面轮廓,同时要求大尺度海面轮廓剖分成表征海面几何特征的海面面元,每个面元看成具有微粗糙度的面元。根据不同面元的粗糙度,采用不同电磁散射计算方法。对于微粗糙面元采用微扰法来计算该面元的电磁散射,对于粗糙度大的面元,如包含破碎海浪的面元采用积分方程法(IEM)算法[13-14]。整个海面区域的远区场则基于散射中心理论[15-17]叠加得到。该混合面元法综合了解析算法和数值算法的优势,在保证一定计算精度的条件下,实现高效计算超电大尺寸的快速电磁散射。
1 海面几何模型
本文将海面视为具有双尺度特性的粗糙面,海面的轮廓采用线性滤波法生成,采用文氏海谱生成海面轮廓。文氏谱[18]是我国中科院文圣常院士团队在二十世纪八九十年代,通过对我国渤海、黄海、东海和南海等大量观测数据进行拟合,得到了与我国近海海情十分吻合的海谱,并且与能够反映北海观测数据的JONSWAP谱的结果相对应,间接验证了文氏谱能够表征北海观测数据,从而证明了该谱的通用性。
该谱的有因次表达形式如下:

(1a)
(1b)
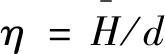
基于线性滤波法生成的海面轮廓往往将海面的毛细波省掉,为了准确刻画海面几何模型,将生成的海面轮廓划分为不同的面元,每个面元根据几何位置不同,设置不同的微粗糙度,如图1所示。

图1 双尺度海面生成示意
2 海面电磁散射计算的混合面元法
面元法将海面视为由各个微粗糙面元构成的具有文氏谱海面轮廓的大型海面,在电磁散射计算过程中,各个面元的散射视为独立不相干,因此整个海面的电磁散射为各个面元散射贡献的叠加。本文将粗糙面电磁散射计算的IEM算法和散射中心理论相结合用于大型海面的电磁散射中。首先采用线性滤波法生成大尺度文氏谱的海面轮廓,再将海面看成剖分成为微尺度粗糙面元。对微尺度粗糙面元的电磁散射采用IEM算法,整体海面电磁散射则有所有面元的散射贡献通过散射中心理论叠加计算。最后散射系数由蒙特卡洛法多次计算随机海面平均得出。电磁散射计算混合面元法的算法示意图如图2所示。

图2 混合面元法计算示意
2.1 面元算法模型的选取
对于出现海浪破碎波的面元,采用IEM算法[10];对于相对平滑的面元,采用SPM算法。本文采用面元斜率准则来判定该面元中是否包含破碎波,斜率阈值设置为0.586,即面元中包含斜率大于0.586的点则认为该面元中含有破浪,将采用IEM算法来计算该面元的电磁散射;若面元中的点斜率都小于0.586,则认为该面元相对平滑,采用SPM算法来计算该面元的电磁散射。
IEM算法将散射场分成2部分:基尔霍夫近似部分和补充部分。IEM算法的代数表达式如下:
(2)
式中,p=v,h;fvv=2Rv/cosθ;fhh=-2Rh/cosθ。
(3)
(4)
(5)
(6)
式中,ω,ω(n)为粗糙面的谱函数;θ为该面元处的局部入射角;k为入射波空间波数。
2.2 基于散射中心理论的远区场计算
散射中心的概念是从理论分析中产生的,并无严格的数学证明。根据电磁理论,每个散射都相当于一个斯特拉顿-朱(Stratton-Chu)积分中的一个数学不连续处,故从集合外形出发,可以认为目标表面曲率不连续处即可形成散射中心。依据散射中心幅度和位置的方位依赖性,可将复杂目标的散射中心分为3类:局部散射中心(LSC)、分布型散射中心(DSC)和滑动型散射中心(SSC)[5-6]。
局部型散射中心的形成机理通常为尖顶绕射、角绕射、边缘绕射以及其他类型的目标表面不连续处的散射等。根据局部散射中心的特点以及属性散射中心模型关于该类散射中心的描述,现将其单基地散射中心模型表达式总结为:
(7)

3 算例
3.1 算法有效性
为验证散射中心理论在海面电磁散射计算中的有效性,计算一粗糙海面,一种方法采用KA计算整个海面区域,另一种方法则采用基于散射中心理论的面元法。为便于对比,每个微粗糙面元的散射幅度也采用KA计算。算例参数: L波段,频率1.25 GHz,海面大小50 m*50 m,在x,y方向平均分为5段,即25个面元。从图3中可以看出,采用本文所提面元法对粗糙海面在中等入射角度(10°~45°)范围内,与传统基尔霍夫近似算法结果吻合得很好。同时,由表1可以看出,通过KA计算该算例用时51.2 s,而通过本文所提混合面元法用时仅为9.3 s,本文所提面元法仅为KA算法的1/5。
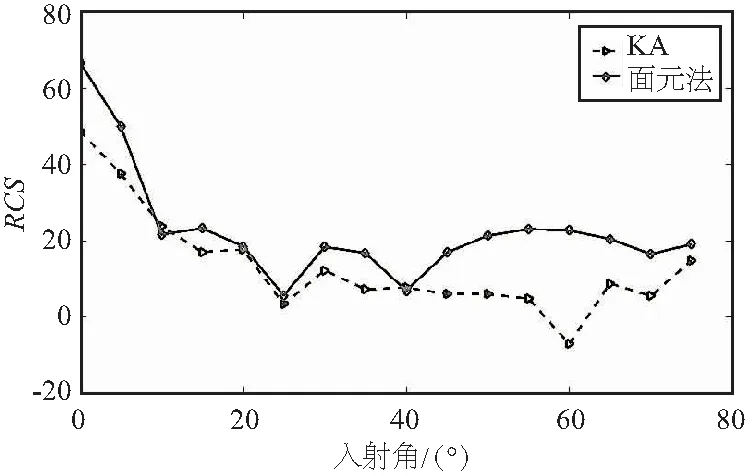
图3 面元法和传统KA对比
表1 计算时间对比

方法计算时间/sKA51.2面元法9.3
算例参数: L波段,频率1.25 GHz,大小为200 m*200 m的PM谱海面。海上19.5 m处风速设为7 m/s,面元大小设为10 m*10 m,面元均方根高度设为0.4 cm;相关长度为4 cm;海水介电常数为72.6-j*69.3,VV极化。图4为采用蒙特卡洛法分别计算10,20,30,40次后平均得到的雷达散射系数。可见,通过多次蒙特卡洛平均,海面电磁散射系数趋于平滑稳定。

图4 蒙特卡洛法对比
3.2 含卷浪海面电磁散射特性分析
本文算例中,均采用40次蒙特卡洛平均散射系数。算例考察一含有卷浪文氏谱海面:L波段,频率25 GHz,大小为200 m*200 m的PM谱海面。海上19.5 m处风速设为7,9 m/s,面元大小设为10 m*10 m,面元均方根高度设为0.4 cm;相关长度为4 cm;海水介电常数为72.6-j*69.3,VV极化。随着风速的升高,海面发生破浪的概率升高,由图5可以看出,随着入射角增大,破浪对海面后向散射的影响增强,入射角度变大,含破浪多的海面,后向散射强于破浪概率小的海面。

图5 不同风速下的海面散射系数
4 结束语
为实现高精度高频雷达体制下海面电磁散射回波的快速高效计算,提出一种基于散射中心理论的混合面元法,该方法通过建立具有双尺度粗糙特性的三维海面几何模型,根据面元是否包含破碎海浪还判定采用不同的面元电磁散射计算方法,最后根据散射中心理论将各个面元的远区散射场叠加,得到整个雷达波束照射区域海面电磁散射回波。该算法在保证一定精确度的同时,提高了海面电磁散射计算的效率,为三维动态海杂波的特性分析建立了必要的电磁散射计算平台。

