一种嵌入射频指纹的半监督辐射源识别方法
姚君宇,许小东
(中国科学技术大学 电子工程与信息科学系,安徽 合肥 230031)
0 引言
SEI能通过接收信号中的细微特征识别不同的无线电发射机[1],在不同领域拥有广泛应用,例如军事情报侦察、电子对抗以及设备故障诊断等。传统的SEI方法将SEI问题看作一种模式识别问题[2],首先从信号中人工提取RFF特征,然后将其通过分类器来完成识别任务。在RFF特征中,双谱特征[3-4]由于其良好的抗噪性能和较稳定的分离性而被广泛使用。然而由于其主要通过信号的相频特性来对辐射源进行识别,难以提取辐射源的其他内在细微特征[3]。在非协作通信情况下,无法取得完整的辐射源先验信息,仅使用双谱特征难以对辐射源进行准确识别[4]。
近年来,深度学习方法在SEI的应用中取得了进展。通过神经网络来直接学习信号中的深层隐性特征[5-6]使得深度学习方法相较于特征提取方法获得了更高的识别率,并且降低了对信号先验信息的需求[7]。在非协作通信中,通常只能得到大量无标签数据和少量有标签数据。为了应对这种标签数据集缺失的情况,迁移学习[8]、数据增强[9-10]都是可行方法,然而这些方法需要数据的先验信息或是庞大的初始样本数据库。相比之下,贝叶斯神经网络[11]不需要任何先验信息和初始样本,具有较好的通用性。贝叶斯神经网络通过提升网络的泛化能力,来克服训练集稀少时遇到的过拟合问题。在图像[12]以及文本识别[13]等领域,贝叶斯神经网络已经被证明可以在标签训练集更少的情况下达到和传统深度学习方法相同的识别率,并且通过半监督学习[14]可以更好地利用大量的无标签数据。
为了克服非协作通信中的问题,在神经网络框架下,使用双谱灰度直方图特征和贝叶斯CNN相结合,通过回归拟合射频指纹特征来指导CNN训练,并且结合了基于模糊度的半监督学习方式,在有限的标签数据下,进一步提高辐射源的识别率。在模拟数据集和真实数据集中,对提出的方法和其他SEI方法进行了性能比较。
1 问题描述与相关知识
1.1 问题模型
SEI是从接收信号中提取出辐射源的本质差异信息,以此分辨不同辐射源,从而识别辐射源个体。一个典型的SEI系统如图1所示。
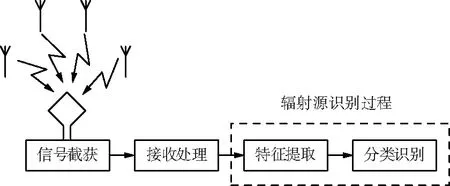
图1 SEI基本过程
考虑只有一个接收器截获来自某个感兴趣区域的可能无线信号。假设可以单独捕获每一个发射机的信号,不存在盲分离的问题。每个发射机的发射信号为:
si(t)=gi(mi(t),qi),i=1,2,…,N,
(1)
式中,si(t)包含了需要传送的调制信息mi(t)和设备指纹信息qi;gi为辐射源发射机模型,包括功放、相噪和滤波器等多种器件的非线性因素的影响,这些器件的相互影响正是指纹特征p的来源。接收信号可以表示为:
yi(t)=si(t)⊗hi(t)+ni(t),i=1,2,…,N,
(2)
式中,hi(t)表示发射机与接收机之间的信道;ni(t)表示零均值的加性高斯白噪声;⊗表示卷积运算。
接收机接收的信号经变频、A/D变换等处理也会受接收机器件非线性影响,输出信号为:
(3)

1.2 贝叶斯CNN
与传统CNN不同,贝叶斯CNN(BCNN)[15]所训练出的网络模型参数不是固定值,而是各个参数的分布,如图2所示。

图2 BCNN和传统CNN的区别
对于BCNN来说,需要求的是权重矩阵W在训练数据X和标签Y下的后验分布p(W|X,Y)。一般来说,这种后验分布是不易计算的,使用变分推理来近似它[15],即通过最小化权重近似分布和完全后验之间的KL散度:KL(q(W)||p(W|X,Y))来学习网络权重q(W)的分布,而最小化KL散度等价于最大化对数似然下界(Log Evidence Lower Bound,ELBO),即:
(4)
式中,F为关于Y和X的函数。
本文中用于实现构建BCNN的方法是dropout[16],通过在每个卷积层间使用dropout来使得第i层的权重分布q(Wi)为:
(5)
式中,zi,j为具有概率pi的伯努利分布随机变量;而Mi为需要优化的变分参数。diag(•)运算符将向量映射成对角矩阵。
对于伯努利近似分布,式(4)中的积分是难以计算的。于是可以通过蒙特卡洛积分来近似计算得到LVI的无偏估计:
(6)
式中,E(·,·)为softmax损失函数。通过蒙特卡洛积分近似的关于新的输入x*的模型预测结果y*可以表示为:
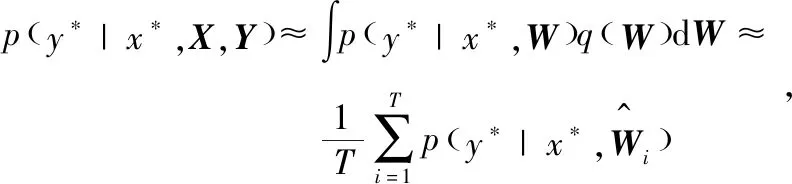
(7)
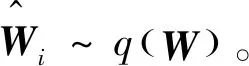
2 嵌入射频指纹的BCNN SEI算法
2.1 基于双谱的灰度直方图特征
提出一种新型的射频指纹,利用信号的双谱来设计特征向量。双谱可用于描述信号的不对称程度和非线性,并测量信号偏离高斯分布的程度。为了提取指纹特征,采用双谱统计量来表示接收信号的交叉频率依赖性。一般来说,双谱Bx(ω1,ω2)可以表示为:
(8)
式中,c3x(τ1,τ2)表示τ1,τ2为时延的信号x(n)的三阶累量,即:
c3x(τ1,τ2)=E{x*(n)x(n+τ1)x(n+τ2)},
(9)
其中,E{•}为期望;上标*为共轭。
为了构造特征向量ht,首先将(ω1,ω2)分割成若干个分辨率为Δω的频率区间。然后将双谱Bx(ω1,ω2)的实部和虚部分开转换为一个新矩阵:
(10)
式中,Re,Im分别为实部与虚部,再将R转化为λ比特的灰度图[17]:
(11)
式中,Gm,n为灰度图的第(m,n)个值;Rm,n为双谱图的第(m,n)个值。
最终在灰度图上通过统计得到一个k比特的灰度直方图特征向量ht:
(12)
式中,ni为灰度值在第i个区间的像素个数;MN为图中像素总数。
2.2 算法结构与步骤
将双谱直方图特征提取用CNN回归代替后与BCNN与相结合的网络结构RFF-BCNN如图3所示。

图3 SEI网络结构
图3中,左侧所示的子网络即回归拟合直方图特征的CNN网络,是数层1D卷积层和数层全连接层组成的1D-CNN,右侧的子网络完成SEI,为数层贝叶斯卷积层和数层全连接层组成的BCNN。将卷积层视为特征提取器,作用是将原始数据映射到一个新的高维特征空间,全连接层的作用则是将学到的高维分布式特征映射到样本标记空间。可以看出左侧子网络的全连接层对于SEI任务来说是冗余的,因为其卷积层输出可以看成双谱直方图特征的高维近似表示,而右侧子网络的全连接层则将2组隐含特征映射到辐射源类别。需要指出的是,左侧子网络的参数是通过预训练设置的,作为双谱直方图的特征提取器,不再参与右侧SEI的子网络训练过程中。
在此基础上,再使用基于模糊度的半监督学习方法[18],用给无标签数据打上伪标签的方式扩大可用训练数据集,以达到更好的识别率。通过将无标签数据输入已训练的神经网络模型,对输出结果的模糊度进行计算,从中筛选出低模糊度数据对其打上伪标签并加入训练数据的方式来增加标签训练集的大小。模糊度的计算式如下:
(13)
式中,μ为输入的无标签样本;μi为神经网络输出的μ关于第i个类的隶属度;N为总类别数。
半监督学习的分布训练步骤如图4所示,其中的神经网络模型即为图3所示网络。
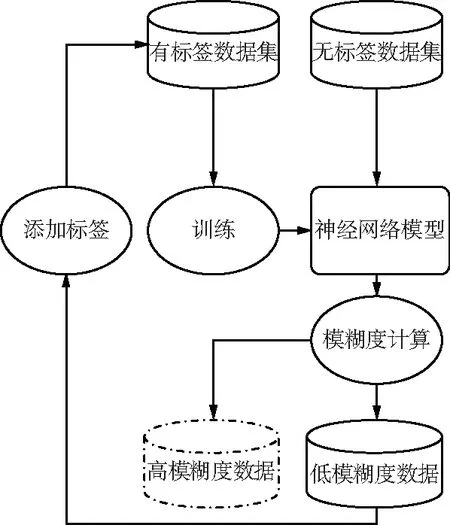
图4 半监督学习训练过程
步骤1:以训练数据XT和对应的标签YT训练图4中的神经网络N;

步骤3:以门限ξ将XS分为低模糊度数据集XLOW和高模糊度数据集XHIGH;
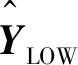
步骤5:重新训练神经网络N。
3 实验分析
3.1 实验数据及参数配置
下面评估提出的网络结构的性能,并通过与其他SEI算法进行比较来展示其性能优势。实验中,基于Python 3.6的Tensorflow搭建了图3中的网络。2个子网络均采用Adam优化器,在一块NVIDIA GTX1080TI的GPU上对网络进行训练。
实验主要在2个数据集上进行:
① 模拟数据:使用Matlab程序生成数据集。基于泰勒功率放大器(PA)模型、BPSK调制、瑞利衰落信道,生成5类信号通过5个具有不同SNR的PA,每个类别由每个SNR的10 000个训练样本组成。
② 采集数据:在实验中使用的无线电时域信号样本取自零中间的实际采样频率IQ正交数据。信号来自同一制造商、相同型号和相同工作模式的5个不同的短波电台和5个不同的超短波电台。电台输入源为3组不同的音频数据。采集参数如表1所示,采集环境为户外,常温,发射机与接收机间距200 m。
表1 采集信号参数
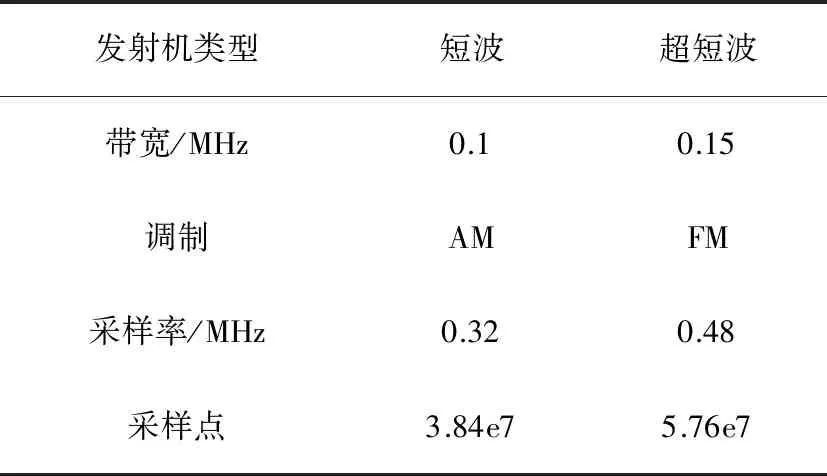
发射机类型短波超短波带宽/MHz0.10.15调制AMFM采样率/MHz0.320.48采样点3.84e75.76e7
需要补充的是用来回归拟合的CNN子网络使用模拟数据和真实数据进行预训练,在RFF-BCNN的训练过程中这部分网络参数不再参与训练。
3.2 实验结果与分析
3.2.1 识别性能与信噪比的关系。
信噪比是影响分类准确性最常见的因素,在实验1中,对于模拟数据集,本文比较了不同方法在不同信噪比下的识别性能。图5比较了模拟数据集在0~20 dB信噪比下的识别性能,网络训练配置如表2所示,在本次实验中各个方法均有足够的训练样本。包括:① 本文所提模型RFF-BCNN,② 1D-CNN模型[10],③ 对双谱直方图特征进行分类,使用SVM分类器,④ 对希尔伯特-黄谱特征[18]进行分类,使用SVM分类器,⑤ 使用精确的双谱直方图特征代替回归子网络的方法的识别性能。从图5中可以看出,深度学习方法相对于特征提取方法在信噪比降低时的性能衰减更小,并且在各个信噪比下深度学习方法都表现出了更高的识别率。而由于使用射频指纹特征辅助网络训练,RFF-BCNN相对于1D-CNN[10]有2%~5%的性能提升。通过①和⑤的对比可以看到,回归子网络在对性能几乎没有影响的情况下,将特征提取和分类网络并行,提高了计算效率。
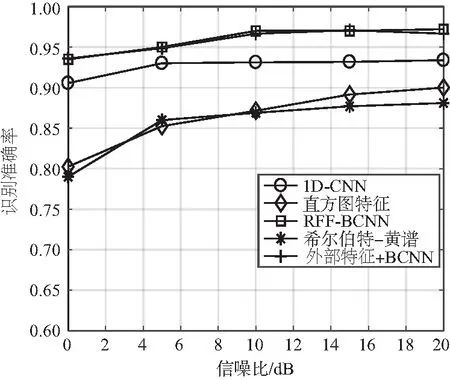
图5 不同信噪比下的SEI性能
表2 网络训练配置

网络配置真实数据模拟数据类别数55数据集大小5000050000训练集大小500~450025000batchsize100200模糊度门限ξ1/6-学习率0.0050.005迭代步长100100
3.2.2 不同训练集大小下的识别性能
在实验2中,使用了真实采集的数据来展示RFF-BCNN在少量标签训练样本下的识别性能,网络训练配置如表2所示。
在短波数据集以及超短波数据集下,比较了①本文所提出的RFF-CNN算法、②仅使用真实标签的RFF-CNN算法、③1D-CNN方法和④基线BCNN方法,实验结果如图6所示。
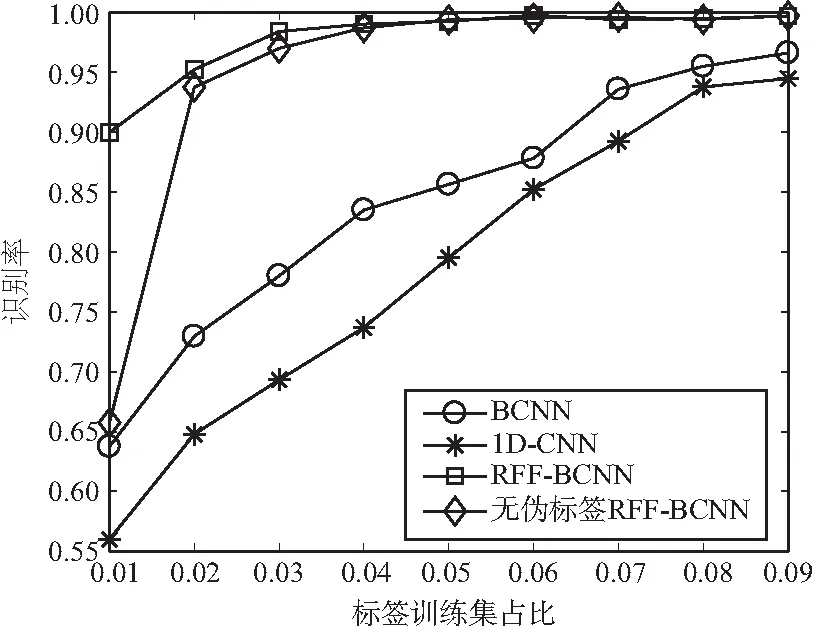
(a)超短波数据集
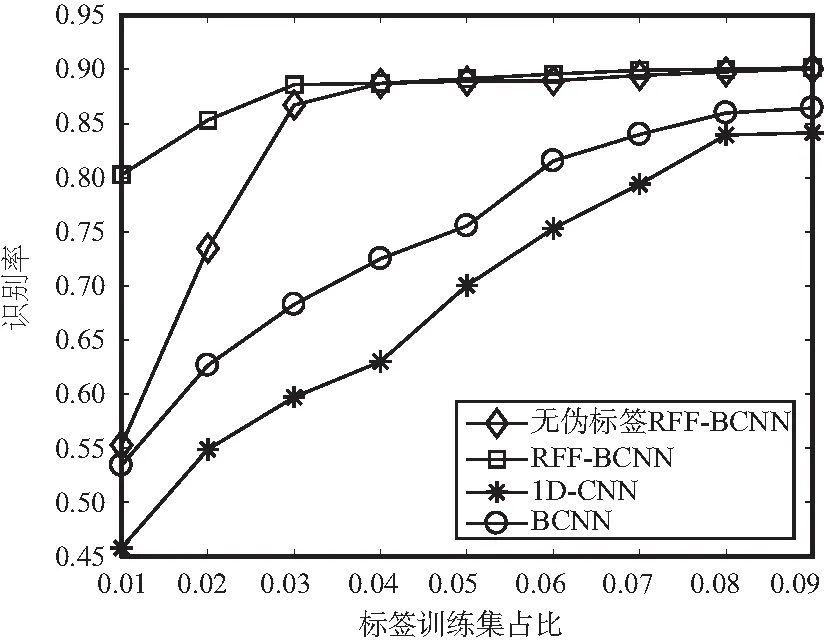
(b)短波数据集图6 不同训练集规模下的识别性能
图6中横坐标表示初始训练集规模,纵坐标表示识别准确率。从图中可以明显看出,不论是在超短波还是短波数据集上,各个算法的识别性能随着训练集规模的变化表现出基本相同的变化趋势,即随着训练集规模的增大识别率也在逐渐升高。由于BCNN优秀的泛化性能,其在小规模训练集下的识别率性能要优于1D-CNN。而对于仅使用真实标签的RFF-BCNN,由于有着射频指纹特征作为网络训练的辅助,并且回归拟合指纹特征的子网络不受训练集规模影响,其达到性能阈值所需要的训练集规模远小于普通的深度学习方法。而在具有相同的初始训练集规模的情况下,半监督学习相当于提升了训练集的规模,所以在初始训练集规模很小的情况下,RFF-BCNN表现出远优于其他方法的识别性能。
4 结束语
提出了一种新型的用于SEI的半监督深度学习算法(RFF-BCNN)。基于BCNN模型,结合传统特征提取方法以及半监督的优点,将射频指纹特征提取融入到深度学习框架中,并且通过基于模糊度的半监督学习方法利用了无标签样本。在模拟和真实数据集上的实验表明,在有标签训练样本集规模较小时,RFF-BCNN相较于1D-CNN模型有着5%~20%的性能提升。

