递推式xn+1=xn(xn-1)的性质探究
2020-01-10 06:38:44浙江省平阳中学325400何龙泉
中学数学研究(江西) 2019年12期
浙江省平阳中学 (325400) 何龙泉
递推式xn+1=xn(xn-1)由迭代xn+1=f(xn)和函数f(x)=x(x-1)构成.由f(x)=x得x*=0,x**=2,又f′(x)=2x-1,于是|f′(0)|=1,
|f′(2)|=3>1,故由不动点稳定性判定定理[1]:x0是函数f(x)的不动点,则当|f′(x0)|<1时,通过迭代an+1=f(an)(a1在x0附近)得到的数列{an}极限存在,并以x0为极限.此时,称x0为稳定的不动点;而当|f′(x)|>1时,数列{an}发散,称x0为不稳定的不动点.由此知:x**=2为不稳定的不动点,不动点x*=0的稳定性与首项x1有关,本文将对数列的性质作进一步的探讨.
一、数列{xn}的性质
具体地说,对于不同的x1,由递推式xn+1=xn(xn-1)得到的数列{xn}有以下性质:
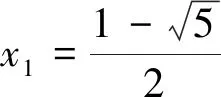
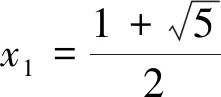
(3)当x1<-1或x1>2时,{xn}是递增数列且发散.
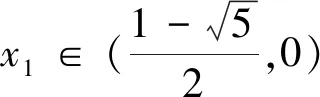
(5)当x1∈(0,1)时,x2 在证明上述结论之前,我们先来证明两个易证结论. 图1 下面我们来证明上面数列{xn}的性质. 性质(1)和(2)显然成立的,证明略. (1)求首项a1的取值范围; (2)证明:对任意n∈N*,都有an+1>an. 解:(1)由已知a1>0,(ⅰ)若a1∈(0,1],则a2≤0,不合题意; (2)由(1)知an+1-an=an(an-2)>0,所以对任意n∈N*,都有an+1>an. 对于递推式xn+1=xn(xn-1)性质的探索只是对该类递推式探究的一个方面,这样的研究对于教学、命题都大有裨益.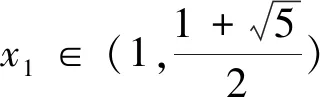
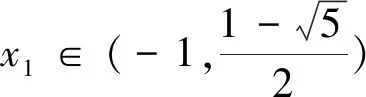
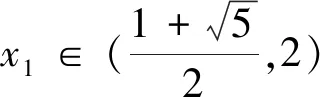
二、性质的证明
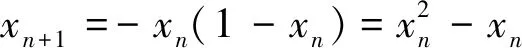
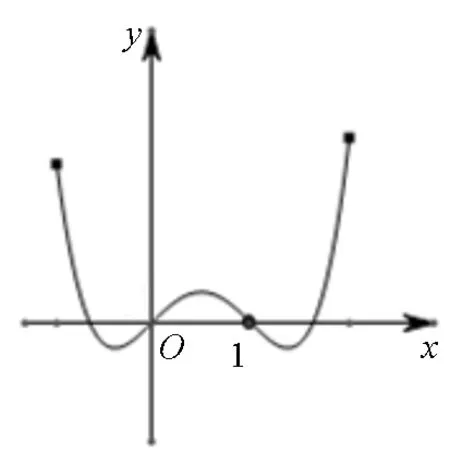
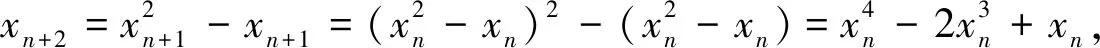
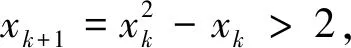
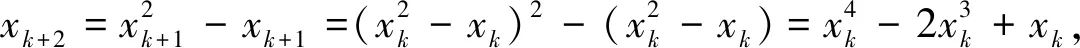
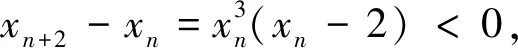
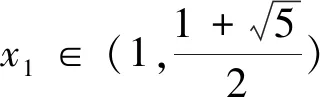

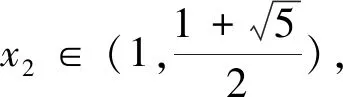
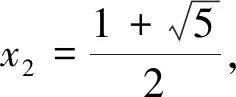
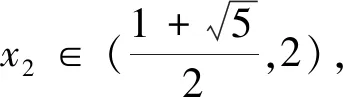
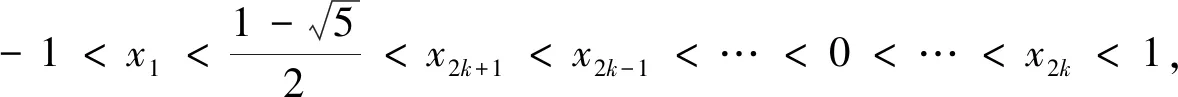
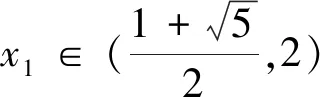
三、性质的应用
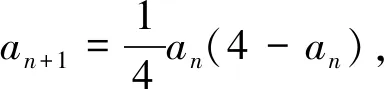
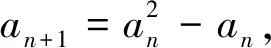
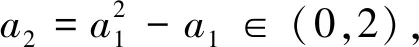
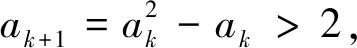
猜你喜欢
Chinese Physics B(2024年3期)2024-03-25 09:30:02
金桥(2023年1期)2023-01-13 06:16:34
Plasma Science and Technology(2022年1期)2022-02-15 11:08:20
数学物理学报(2020年4期)2020-09-07 09:14:16
边疆文学(2020年5期)2020-05-22 02:58:58
西夏研究(2020年1期)2020-04-01 11:54:40
中等数学(2019年12期)2019-05-21 03:22:16
陶瓷科学与艺术(2018年1期)2018-07-13 09:36:16
中国三峡(2017年9期)2017-12-19 13:27:43
河北科技大学学报(2015年6期)2015-03-11 16:16:46

