全空间中具时间依赖参数的p-Laplacian方程的拉回吸引子

王 怡， 马巧珍

(西北师范大学数学与统计学院， 兰州 730070 )

1 引 言

文献[1]考虑了单项渗透问题.假设有一种可压缩流体在均匀、各向同性的刚性多孔介质中流动.根据质量守恒定律有

(1)

其中正常数θ为介质的孔隙率，u为流体的渗透速度.在非牛顿多方气体流中，上式中的气体动量密度

(2)

而压力和密度满足状态方程

P=cuγ

(3)

其中λ与视粘度μ有关，μ不仅取决于切变率而且取决于施加切变率的时间,α>0 是物理常数，c和γ是正常数. 结合以上方程，我们可以得到

ut-div(ε(t)|u|p-2u)+f(x,u)=g(x)

(4)

在带参变量t的赋范空间中时间依赖全局吸引子和拉回吸引子的存在性.

本文考虑外力项也依赖于时间t的p-Laplacian方程

(5)

其中p>2,f(x,u)=a(x)f1(u)满足假设：

f1(0)=0,α|u|p-β|u|2≤f1(u)u≤

γ|u|p+δ|u|2

(6)

f1′(u)≥c1

(7)

a(·)∈L1(Rn)∩L(Rn),a(x)>0,

∀x∈Rn,

(8)

这里α，β，γ，δ为正常数，α>β与文献[2-3]相同.

设ε(·)∈C1(R)是单调递减函数并满足

(9)

且存在L>0,使得

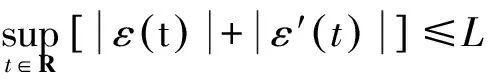
(10)

(11)

其中σ>0为恰当的常数. 当ε(t)为常数时，方程(5)的全局吸引子和一致吸引子的存在性已有研究[4-6].文献[7]研究了参数为Dλ的p-Laplacian方程拉回吸引子的存在性和上半连续性，其中Dλ(t)∈L([τ,t]×Ω),在[τ，t]×Ω上，0<β≤Dλ(t,x)≤M几乎处处成立.对每个λ∈[0,],∀x∈Ω,s,t∈[τ,T],有

|Dλ(sx)-Dλ(tx)|≤Cλ|s-t|θ λ,

且在L([τ，t]×Ω)上当λ→λ1时，Dλ→Dλ1.最近，文献[8-9]分别得到了plate方程强拉回吸引子的存在性和带有非线性阻尼的非线性弹性杆振动方程时间依赖吸引子的存在性.

在无界域上研究p-Laplacian方程所对应的无穷维动力系统吸引子的存在性时，Sobolev嵌入没有紧性是一个本质的困难.为克服这一困难，我们利用了文献[10]中提出的尾部估计方法.本研究是文献[11]的推广.

2 预备知识

设X是完备的距离空间.对t∈R,令Xt是一族依赖于时间的赋范空间.称双参数算子族{U(t,τ)}t≥τ是一过程，若它满足

(i)U(t,τ)=U(t,r)U(r,τ),∀t≥r≥τ;

(ii)U(τ,τ)是Xτ上的恒同映射，∀τ∈R;

(iii)U(t,τ):X→X连续，t≥τ≥R.

如果对每一个有界集D⊂X上式都成立，则称K在t时刻拉回吸引有界集.

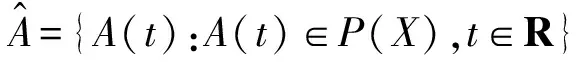
(i) 对于任意t∈R,A(t)是X中的紧集；

(ii) 对过程U(t,τ)而言，A(t)具有不变性，即

U(t,τ)A(τ)=A(t),∀-<τ≤t<+,

A(t)拉回吸引空间X中任意有界集D，即对任意的t∈R,有

其中dist(A,B)表示集合A和B的Hausdorff半距离.

则A(t)⊂C(t).

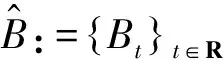
3 主要结果

记L2(Rn)中的内积为〈·，·〉，范数为‖·‖.由ε(t)的假设可知，对固定的t,τ∈R,空间Xt与Xτ，Yt与Yτ的范数等价，且当t→+时，等价常数爆破，见文献[12].由标准的Galerkin方法，以下定理成立.

定理3.1假设f,ε,g满足(6)～(11)式.则对任意的τ∈R，初值uτ∈L2(Rn)和任意的t≥τ,方程(5)存在唯一解u∈C([τ,t];L2(Rn)),且映射uτ→u(t,τ,uτ)在L2(Rn)中连续.

由上面的定理可知，在Xt中可以定义连续过程

U(t,τ):U(t,τ)u(τ)=u(t)

(12)

其中u(t)是问题(5)的解.现在给出本文的主要结果：

为了证明定理3.2，首先证明下面几个引理.

引理3.3假设f,ε,g满足(6)～(11)式，则有

其中Q是不依赖与t,τ的正常数，

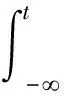
证明 证明过程类似于文献[3]中的证明,只是外力项的估计不同.用ε(t)u与(5)式在L2(Rn)中做内积，可得

〈g(x,t),ε(t)u〉

(13)

由于f(x,u)=a(x)f1(u)，应用(6)式可得

〈a(x)f1(u),u〉≤

δ‖a‖L(Rn)‖u‖2

(14)

由g的假设及Cauchy不等式，有

2〈g(x,t),ε(t)u〉≤

(15)

其中ν为充分小的正常数.由(13)～(15)式并结合ε′(t)<0得

(16)

注意p>2,故

(17)

由于a(x)>0，故存在正常数α0，使得a(x)≥α0>0,∀x∈Rn.由(17)式和a(x)的假设及嵌入定理得到

Qε(t)‖u‖2

(18)

这里Q为不依赖于t,x的正常数.将(18)式代入(16)式可得

(19)

上式两端同乘eQ s有

(20)

对(20)式关于s在[τ，t]上积分得

ε(t)‖u(t)‖2≤e-Q(t-τ)ε(τ)‖u(τ)‖2+

(21)

这里C1是不依赖于t,x的正常数.结合(11)式得到Rt<,且这样，由引理3.3可知，(12)式定义的过程U(t,τ)拥有一个有界的拉回吸收集{Bt}t∈R,其中

注1引理3.1的证明过程结合(16)式可得

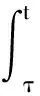
(22)

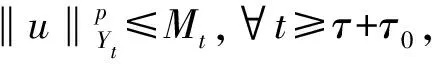
PLe-Q τ‖g(s)‖2ds.

证明 用ε(t)ut与(9)式在L2(Rn)中做内积可得

-〈f(x,u),ε(t)ut〉+

(23)

由(7)式及Hölder不等式得

将上式代入(23)式得

(24)

上式两端同乘eQ s，结合ε′(t)<0和(22)式得

(25)

由一致Gronwall引理得

(26)

即

‖g(s)‖2ds

(27)

从而由(10)式可得

(28)

结合(11)式和引理3.3得到

(29)

证毕.

引理3.5对任意的σ>0，当初值uτ∈Bτ时存在正常数k和T>0,使得

(30)

证明 选择合适的光滑函数θ，使得对任意的s≥0有0≤θ(s)≤1.具体地，当0≤θ(s)≤1时有θ(s)=0；当s≥2时有θ(s)=1，且存在一正常数C，使得|θ′(s)|≤C.

(31)

应用ε(t)单调递减的假设及Cauchy不等式，忽略(31)式左边第二项可得

〈-div(ε(t)|u|p-2

(32)

注意到

(33)

(34)

由(6)式得

(35)

将(33)～(35)式代入(32)式可得

(36)

注意到p>2,故

(37)

这里C是不依赖于t,u的常数.由(37)式和a(x)的假设可知存在正常数λ和k0使得当k>k0时有

(38)

将(38)式代入到(36)式得

(39)

故

(40)

上式两边关于r在[τ，t]上积分可得

(41)

下面我们对(41)式的右边两项进行估计.由于uτ∈Bτ，则当τ→-时，对任意固定的t∈R有

(42)

由Lebesgue积分的性质，存在k1(t,σ)使得第二项满足

(43)

注意到

(44)

则存在k2>k使得

(45)

定理3.2的证明 由引理3.3可知u(t,τ)于Xt上存在有界的拉回吸收集{Bt}t∈R.由引理3.4和引理3.5可知u(t,τ)在Xt上是渐进紧的.应用定理2.5和定理3.1，定理3.2得证.