多次水下爆炸作用下钢板动态响应数值模拟
张斐,张春辉,张磊,王志军,周春桂
1 海军研究院,北京100161
2 中北大学机电工程学院,山西太原030051
0 引 言
随着现代科技的高速发展,反舰武器已从单一作战发展为集群作战,舰船舷侧不可避免地会受到战斗部的多次攻击,其爆破能力会造成舰船不同程度的破损,因此舰船水下抗爆性能的研究受到了前所未有的重视[1-2]。舰船舷侧受到反舰武器攻击时,其材料与结构会发生应变率效应及塑性变形等非线性问题[3]。由于舰船是由大量板、梁、杆等拼装而成的大型钢结构[4],直接研究舰船结构与材料的抗爆性能具有一定困难,通常选取舰船舷侧的典型结构作为研究对象。非接触爆炸载荷作用下舰船舷侧动态响应的研究通常选取固支背空圆钢板为研究对象[5]。国外学者对水下非接触爆炸载荷作用下钢板的动态塑性变形进行了大量试验。美国于1990 年制定了美军标MIL-STD-2149A(SH)[6],确定了船用钢母材及焊缝在快速加载条件下抗断裂性能的评估方法。2010 年,韩国Park 等[7]设计了水下爆炸鼓胀试验装置,测试了船用钢及焊缝在多次水下爆炸加载作用下的塑性变形。2015 年,印度Kumar 等[8]研究了高强度低合金钢在水下的抗冲击性能。
国内于1997 年制定了空爆下测试钢板塑性变形的试验标准,但关于测试多次水下爆炸载荷作用下钢板塑性变形的公开报道尚不多见。目前国内学者的研究主要集中于一次水下爆炸载荷作用下钢板的动态响应。吴成等[9]研究了水中爆炸产生的强冲击载荷作用下固支方板的塑性动力响应过程,推导了固支方板在冲击载荷作用下变形的最终挠度的解析解。谌勇等[10]分析了简支刚塑性圆板受水下爆炸载荷时的塑性动力响应。任鹏等[11]研究了水下近爆载荷作用下舰艇水下结构的动态变形及失效毁伤模式。牟金磊等[12]借助有限元软件MSC.Dytran 研究了固支方板在水下爆炸载荷作用下的动态响应。通过上述研究发现,国外开展的多次水下爆炸鼓胀试验大多为工程项目,国内公开的关于多次水下爆炸载荷作用下钢板动态响应的试验与仿真研究较少。考虑到舰船的实际服役环境以及来自反潜武器集群作战的威胁,舰船结构不可避免地会遭受多次水下爆炸冲击,因此,研究多次水下爆炸载荷作用下钢板的动态响应,可为舰船水下抗爆与防护结构设计提供一定的依据,具有重要的意义。鉴此,本文首先利用有限元软件Autodyn 模拟背空固支45#钢板在多次水下爆炸载荷作用下的动态响应;然后采用自行设计的水下爆炸鼓胀试验装置开展背空固支45#钢板的多次水下爆炸加载试验,并对比分析试验与数值仿真结果。
1 数值仿真计算
1.1 计算工况
水下爆炸数值仿真计算中炸药为球形TNT 装药,药量分别为10,20,30 和40 g,装药距目标钢板中心400 mm(即爆距为400 mm)。相同炸药量下分别对直径600 mm、厚度5 mm 的45#钢板施加连续的3 次水下爆炸载荷。表1 给出了4 种药量下的仿真计算工况,工况编号Cm-n 中,C 为“Case”的首字母,m 为药量,n 为爆炸加载次数。
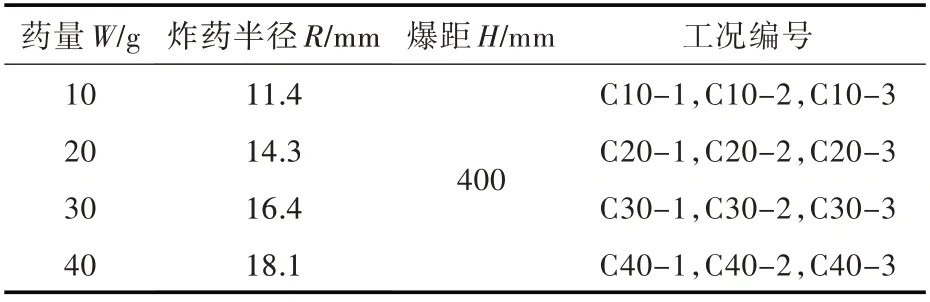
表1 计算工况Table 1 Calculation condition
1.2 有限元模型
由于球形装药、圆形钢板均具有对称性,因此利用Autodyn 建立了如图1 所示的二维1/2 数值仿真模型,主要包括球形装药TNT、背空钢板、边界挡板、水域、空气。其中,边界挡板与背空钢板的材料均选择45#钢,其本构选择考虑应变率效应的J-C 本构模型,材料参数如表2 所示。TNT 选用JWL 状态方程描述;空气选用理想气体状态方程描述;水选用Shock 状态方程描述,强度模型为Hydro,其参数均取自Autodyn 材料库。

图1 首次水下爆炸加载的有限元模型Fig.1 Finite element model of the first underwater explosion loading

表2 45#钢参数Table 2 Parameters of 45#steel plate
数值仿真中涉及到固体、气体、液体等多物质耦合,因此选择Autodyn 软件中自带的流固耦合算法。根据黄兴中[13]的研究,冲击波在边界处的反射会影响数值仿真的精度,水域的尺寸至少应为炸药尺寸的50 倍以上。本研究中炸药的最大直径为36 mm,为了尽可能减小边界条件对计算结果的影响,结合前期试算结果,最终水域大小选择为4 000 mm×4 000 mm,同时在水域的边界处添加流出边界条件。水域采用中心网格加密的方法,其中中心网格大小为2 mm×2 mm,其余网格大小为5 mm×5 mm。由于研究对象为固支背空圆钢板,因此在直径为600 mm 的45#钢板背向添加边界挡板,挡板与钢板围成的区域内赋予空气,同时在45#钢板周向与挡板添加如图2 所示的固支边界条件。从图2 中可以看出,钢板的实际抗爆面是直径为380 mm 的圆形区域。固支背空圆钢板与边界挡板的网格尺寸均为1 mm×1 mm。

图2 钢板与边界挡板的边界条件Fig.2 Boundary conditions of the steel plate and the boundary plate
1.3 多次水下爆炸加载的数值方法
Autodyn 模拟多次水下爆炸加载下钢板动态响应的数值方法的核心是将上一次数值计算的结果作为下一次数值计算的初始条件。实际试验过程中,2 次连续的水下爆炸加载过程中有一定的间隔时间,第2 次施加水下爆炸载荷时水域基本恢复初始状态。因此数值仿真时只将第1 次计算得到的钢板结果输出并保存,然后重新建立相同的水域并读取保存的结果后开始下一次计算。图3是爆距为400 mm、炸药量为30 g 时,5 mm 厚的45#钢板第2 次水下爆炸加载时的有限元模型,其中在钢板、边界挡板上添加固支边界条件、水域的边界处设置流出边界条件;材料的本构模型及参数与1.2 节中相同。
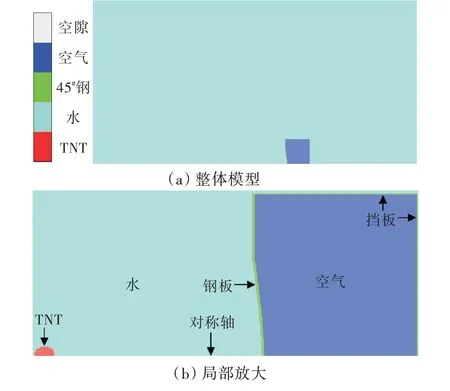
图3 二次水下爆炸加载的有限元模型Fig.3 Finite element model of the second underwater explosion loading
2 数值计算结果与分析
2.1 载荷特性分析
本研究中背空固支圆板实际受爆面的直径为380 mm,爆距为400 mm。根据薛贵省[14]的研究结果可知,背空固支圆板受均布载荷作用。峰值压力是水下爆炸冲击波的重要表征参数,Cole 经验公式可以计算TNT 球形装药在水中爆炸产生的冲击波峰值压力Pm。

式中:Pm为冲击波峰值压力,MPa;W 为TNT 药量,kg;H 为爆距,m;R 为TNT 药包半径,m。
首先通过Autodyn 软件数值计算多次水下爆炸过程中冲击波的峰值压力,然后与Cole 经验公式计算值进行比较,从而验证数值模拟方法的可行性。5 个考核点距离爆心分别为100,200,300,400 和500 mm。C30-1,C30-2 工况中数值模拟的5 个考核点处冲击波压力时间历程曲线如图4 所示。从图4 中可以看出,在炸药量与爆距均相同的情况下,通过Autodyn 软件模拟的2 次水下爆炸加载过程中冲击波压力结果具有良好的一致性。C30-1 工况中数值模拟与经验公式计算的水下冲击波峰值压力结果对比如表3 所示。从表3 可以看出,数值模拟结果与Cole 经验公式计算结果的最小误差仅为6.03%,最大误差不超过19.57%。这表明本研究中的数值仿真模型及方法可以有效地模拟多次水下爆炸加载过程中爆炸流场的载荷特性。

图4 数值仿真中冲击波压力时程曲线Fig.4 Time history curves of shock wave pressure in numerical simulation

表3 冲击波峰值压力计算结果Table 3 Results of the shock wave peak pressure
2.2 钢板变形模式
对上述12 种工况进行数值仿真计算,表4 是12 种工况中钢板塑性变形的测试结果,厚度减薄率是指钢板加载前后同一位置厚度的变化程度,其计算公式为
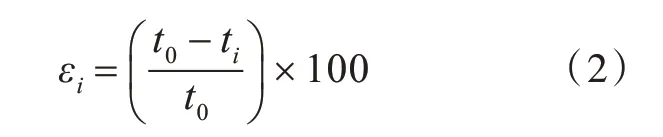
式中:εi为第i 次爆炸后的厚度减薄率,%;t0为爆炸前原始的板厚,mm;ti为第i 次爆炸后的板厚,mm。

表4 数值仿真中钢板的变形结果Table 4 Deformation results of the steel plate in numerical simulation
从表4 中可以看出,当药量相同时,45#钢板的中心挠度随着水下爆炸加载次数的增加而逐渐增大,但增加量却逐渐减少。Murr 等[15]的研究结果表明,钢板在重复冲击载荷作用下会出现剩余强度加强现象,导致钢板内流动应力增加。因此,钢板在连续多次水下爆炸加载过程中弯曲变形逐渐减小,即钢板的中心挠度增加量逐渐减小。进一步研究发现,钢板在连续多次水下爆炸加载过程中,第2 次加载后钢板中心挠度增加量约为首次加载后中心挠度的1/3。
图5 是C10-1,C20-1,C30-1,C40-1 工况下钢板的变形形貌。从图5 中可以看出:4 种工况下钢板受冲击区域均出现了类球冠塑性变形,且变形程度随着装药量的增加而逐渐增大。结合图5与表4 中C10-1,C20-1,C30-1,C40-1 工况下钢板中心挠度的变化情况,可以得到作用在钢板上的峰值压力与中心挠度的关系,如图6 所示。从图6 中可以看出,二者呈线性关系,满足公式:

式中,D为钢板中心挠度,mm。

图5 不同装药量下钢板的变形形貌Fig.5 Deformation of the steel plate morphology under different charge
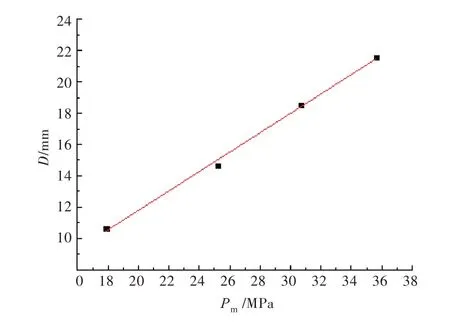
图6 峰值压力与中心挠度的关系Fig.6 Relationship between peak pressure and deflection in the center of the plate
下面以药量为30 g、爆距为400 mm 的工况为例说明多次水下爆炸作用下钢板挠度与厚度减薄率的变化规律。测量C30-1,C30-2,C30-3 工况下钢板受冲击区域半径不同位置处的厚度值,代入公式(1)计算得到不同位置处的厚度减薄率,如图7(a)所示。图7(b)是对应位置处的挠度,其中x 为测量位置处的半径,R 为钢板实际受冲击部分的半径。从图7 可以看出,3 种工况下钢板的挠度与厚度减薄率变化趋势相似,中心位置的挠度与厚度减薄率均为最大,随着离中心位置的距离的增加,其挠度与厚度减薄率呈现减小趋势。在炸药量一定的情况下,挠度增加量随着加载次数的增加而逐渐减小,但厚度减薄率增加量则无明显减小趋势。由体积不变原理可知,首次加载时钢板中心位置以弯曲变形为主,随着加载次数的增加,钢板的双向拉伸变形程度逐渐增大。
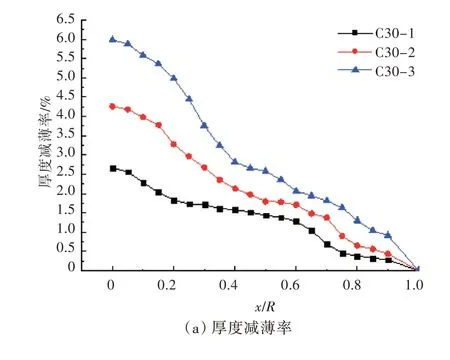

图7 多次加载下钢板挠度与厚度减薄率的变化情况Fig.7 Variation of deflection and thickness reduction of steel sheets subjected to multiple underwater explosions
通过对比C10-3 与C30-1 工况发现,多次水下爆炸加载与单次水下爆炸加载作用下钢板塑性变形并不相同。2 种工况下钢板受冲击区域半径不同位置处的厚度减薄率与挠度对比分别如图8(a)与图8(b)所示。从图8 中可以看出,相同的炸药量下,1 次水下加载与均匀分为3 次连续加载下钢板的变形程度明显不同。单次加载后钢板中心位置的挠度为18.528 mm,而连续3 次均匀加载后钢板中心位置的挠度为14.776 mm,二者相差20.25%;随着距中心位置距离的增加,二者差值逐渐减小,边界处的挠度几乎相同。与连续3 次均匀加载后钢板的变形结果相比,单次加载后钢板的厚度减薄率明显较大。Kumar 等[8]的研究结果表明,相较于传统载荷,钢板在冲击载荷的作用下延展性降低,出现明显的硬化和强化。因此,连续重复水下爆炸载荷作用下钢板的动态塑性变形能力降低,表现为挠度与厚度减薄率均出现一定程度的降低。
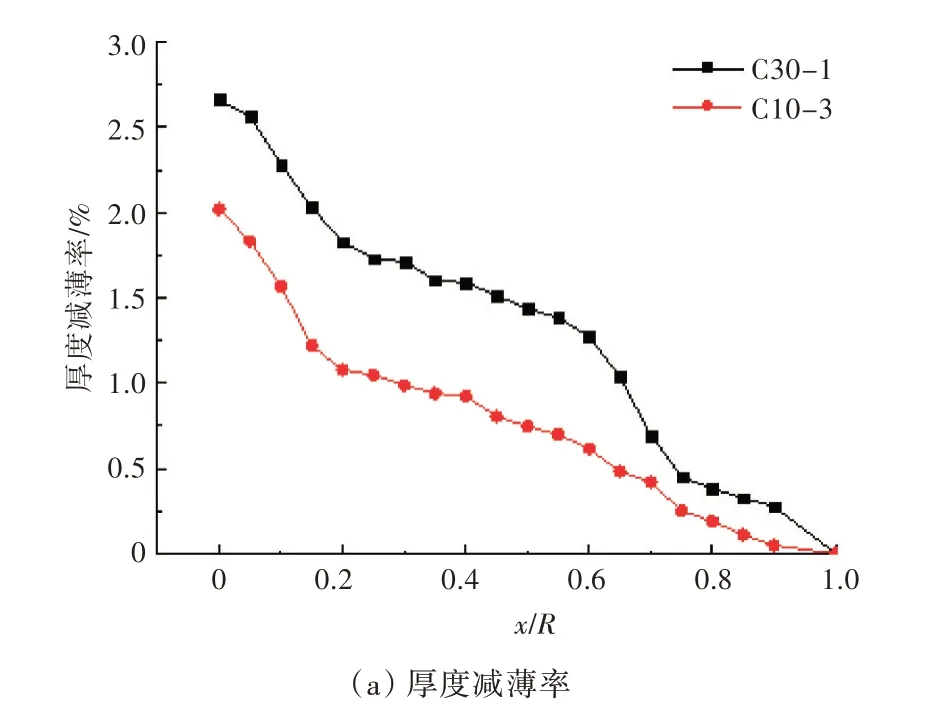
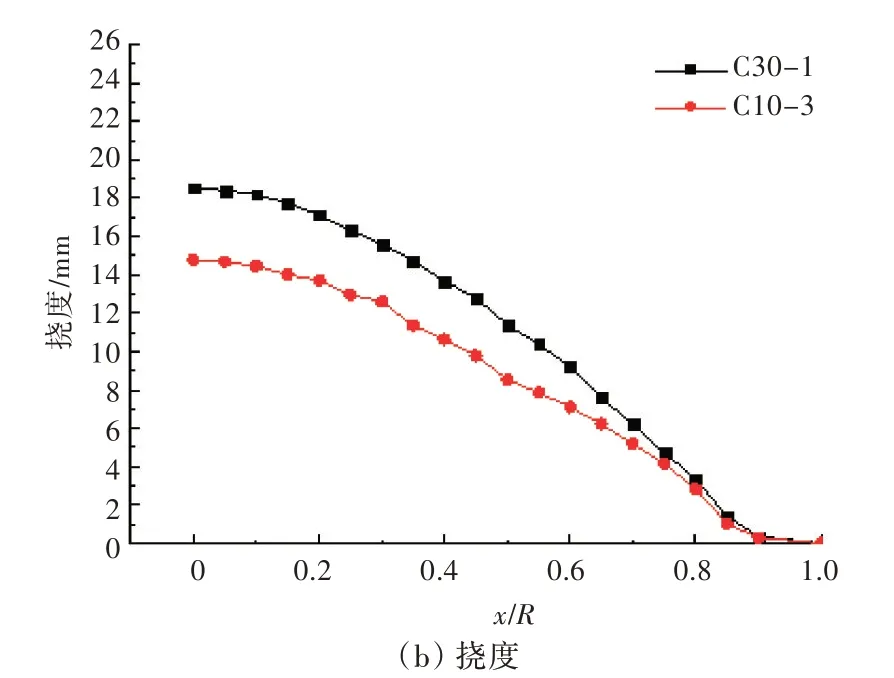
图8 多次加载与单次加载下钢板挠度与厚度减薄率的变化情况Fig.8 Variation of deflection and thickness reduction of steel sheets under multiple loading and single loading
3 试验验证
3.1 试验装置及实施
下面以药量30 g、爆距400 mm 的工况为例验证数值仿真结果的准确性。根据水下爆炸鼓胀试验特点,设计了如图9 所示的水下爆炸鼓胀试验装置,主要由底座、密封圈、压紧螺栓、压铁、固定杆等组成,其中,底座最大直径600 mm、高300 mm,压铁面板厚30 mm。试验前将密封圈、试验板、压铁依次置于试验装置底座上方,采用20 个高强螺栓将上述器材依次固定,保证试验过程中试验板处于背空固支状态。从图9 中可以看出固定后的试验板实际抗爆面为一直径380 mm 的圆形区域。球形TNT 装药通过螺纹杆置于试验板中心的正上方,通过调节装药与试验板的距离(即爆距)来模拟不同爆炸载荷作用下钢板的动态响应。水下爆炸试验水域为9 m×9 m×5 m,试验时装药距水面3 m。
将5 mm 厚(实测厚度为4.78 mm,钢板平整度良好)的45#钢板按试验要求置于水下爆炸鼓胀试验装置,选取TNT 当量为30 g,爆距为400 mm,对其施加3 次连续相同的水下爆炸载荷。距爆源1.24 m 处放置量程为35 MPa 的水压传感器来测量冲击波在水中的传递情况。
3.2 仿真结果与试验结果对比分析

图9 试验装置示意图及照片Fig.9 Schematic and photograph of the test device
试验中通过水压传感器测得距爆源1.24 m 处的水压时间历程曲线以及数值仿真中C30-1 工况中同样位置处的水压时间历程曲线如图10 所示。通过经验公式(1)计算得到距爆源1.24 m 处的峰值压力为10.97 MPa;试验测得峰值压力为11.34 MPa;数值仿真计算得到相同位置的峰值压力为10.12 MPa,其与试验值相差10.76%,与经验公式计算值相差7.75%。三者具有较好的一致性,因此本研究中的数值仿真模型及方法可以较为准确地模拟多次水下爆炸试验中爆炸流场的载荷特性。

图10 试验与仿真的冲击波压力时程曲线对比Fig.10 Comparison of shock wave pressure time history curves between test and simulation
试验与仿真中45#钢背空圆板经3 次连续水下爆炸加载后的变形形貌分别如图11 和图12 所示,从图中可以看出,试验与仿真中钢板经3 次水下爆炸加载后的塑性变形形貌呈类球冠形。试验中钢板经3 次水下爆炸加载后的中心挠度为27.2 mm,而仿真结果为25.28 mm,二者误差仅为7.06%。试验与仿真中钢板受冲击区域半径不同位置处的厚度减薄率与挠度对比分别如图13(a)与图13(b)所示。从图13(a)中可以看出,与仿真结果相比,试验中钢板边界处的厚度减薄率偏大,而其他位置的厚度减薄率相差较小。从图13(b)中可以发现,试验中接近钢板中心位置处的挠度较仿真结果偏大,远离中心位置处的试验与仿真结果一致性良好。这是由于仿真中边界为固支状态,边界处的变形模式主要为弯曲变形;而试验中钢板边界处虽有螺栓固定,但不可避免会存在一定的滑移现象,导致钢板拉伸变形增加,因此试验中钢板中心位置挠度与边界处厚度减薄率相对偏大。整体来看,试验与仿真中钢板的塑性变形结果具有较好的一致性,因此采用本研究中的数值仿真模型及方法可以较为准确地模拟多次水下爆炸载荷作用下钢板的动态响应。

图11 试验中3 次加载后钢板变形形貌Fig.11 Deformation morphology of steel plate after three loading

图12 仿真中钢板变形形貌Fig.12 Deformation morphology of steel plate in simulation
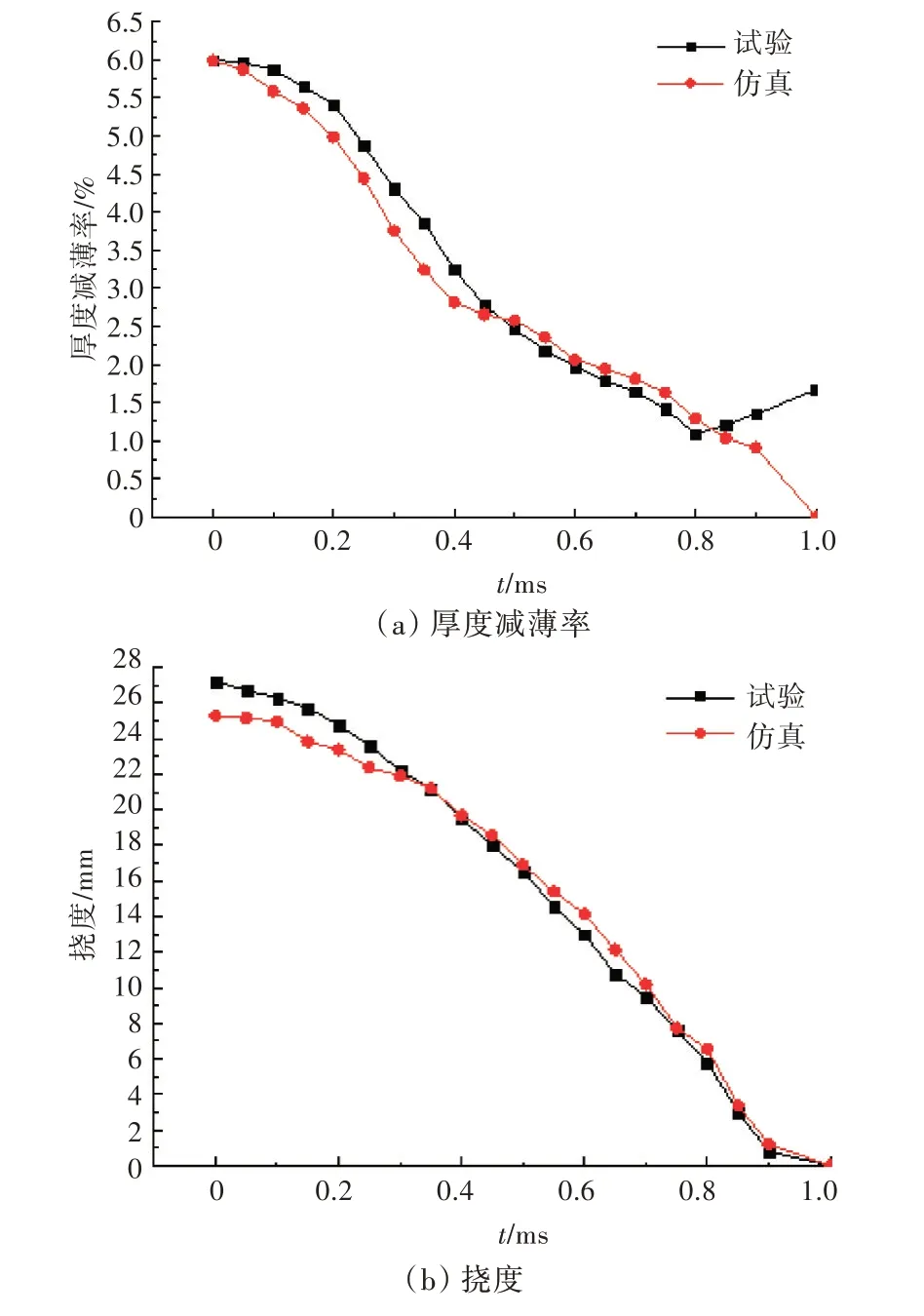
图13 试验与仿真中3 次加载后钢板挠度与厚度减薄率对比Fig.13 Comparison of deflection and thickness reduction ratio of steel plate under multiple loading in test and simulation
4 结 论
本文采用数值仿真与试验相结合的方法研究了多次水下爆炸作用下5 mm 厚的45#钢固支圆板的动态响应,对比分析了试验与仿真结果,主要结论如下:
1)多次水下爆炸载荷作用下,背空固支45#钢板变形形貌呈类球冠形,变形模式以弯曲、双向拉伸变形为主,且双向拉伸变形程度随着加载次数的增加而逐渐增大;钢板塑性变形量随着装药量的增加而增加,且中心挠度与作用在钢板上的冲击波峰值压力成正比。
2)多次水下爆炸载荷作用下,背空固支45#钢板挠度与厚度减薄率从中心位置到边界处呈减小趋势;钢板中心挠度增量随加载次数的增加而减小,第2 次加载后钢板挠度增加量约为首次加载后挠度的1/3。
3)同等药量下,背空固支45#钢板在1 次水下爆炸加载与均匀分为连续3 次水下爆炸加载作用下其塑性变形程度不同,与3 次加载后的结果相比,1 次爆炸加载下钢板的挠度与厚度减薄率均偏大,中心挠度相差20.25%。
4)所选用的数值仿真模型及方法可以较为准确地模拟多次水下爆炸载荷作用下背空固支钢板的动态响应。

