基于模糊PID 的无人帆船航向控制方法

张雪飞，袁鹏*，2，谭俊哲，2，王树杰，2，徐泓燊，孙烨

1 中国海洋大学 工程学院，山东青岛266100

2 青岛市海洋可再生能源重点实验室，山东青岛266100

0 引 言

无人帆船在海上自主航行时，会受到海洋环境的影响，出现一些偏离预定轨迹的状态，因而一个有较强抗干扰能力的航向控制器，对于帆船的航迹保持、循迹航行具有十分重要的意义。

目前，对于航向控制的算法主要有经典PID，Backstepping，Lyapunov，滑模控制、神经网络控制，模糊控制和一些其他相互结合的智能控制方法等［1-2］。国内外很多学者对无人帆船的航向控制做了大量研究。其中，Deng 与Ahmed 等［3-4］通过模糊控制和PD 控制器来控制航向，并应用到了实际的导航路径规划中。Emami 等［5］通过建立Fossen 四自由度船舶数学模型，运用PID 算法实现了对一条小型无人帆船的航向保持控制。王倩等［6］根据操舵的专家经验，归纳总结并制定出了245 条模糊控制规则，并直接以舵角作为输出，对一个1.5m 的帆艇实现了循迹航行控制。沈智鹏等［7］针对无人帆船模型不确定、控制方向和外部环境扰动未知的情况，提出了一种RBF 神经网络自适应动态面航向控制方法。上述研究运用不同的控制方法，实现了对帆船航向的控制，而本文则将研究在不同航速和未知的随机干扰下，帆船航向的稳定性控制。

PID 控制器由于其简单的结构和明确的物理意义，对于特定的场景和精确的数学模型，具有很好的控制特点，仍被广泛应用于实际工程中。然而，传统PID 控制的效果很大程度上取决于其控制参数Kp，Ki，Kd的值，在复杂多变的情况下，很难在线实时调节PID 控制参数，所以，在控制过程中，往往会表现出较大的波动和高频转舵，甚至可能出现不可控的状态［8］。无人帆船在航行过程中会面临风、浪、流等因素的干扰，仅仅依靠传统PID 的调节，往往难以满足准确航向的控制要求。而模糊控制则可以根据实际操作的专家经验，无需确定的数学模型，制定出相应的控制规则，达到理想的控制效果［9］。因此，本文将设计一种结合经典PID 技术的模糊自适应控制器，根据调节PID 控制参数的实际经验，制定出相应的模糊控制规则，实现对PID 控制参数的动态调节，从而达到对帆船稳定控制的目的。

1 无人帆船数学运动模型

1.1 帆船模型参数

本文以自主设计的无人帆船模型为仿真研究对象。该船体（附体）与风帆主尺度如表1 所示，舵剖面选用NACA 0018 翼型。

1.2 帆船运动坐标系

在实际海面运动过程中，一般可以将帆船近似为一个具有六自由度的刚体。为便于对帆船的运动描述，建立了如图1 所示的2 种右手坐标系。其中，o0-x0y0z0是以t=0 时刻船舶重心为中心的惯性坐标系，o0-x0轴为静止水面正北方向，o0-y0轴为静止水面正东方向，o0-z0轴垂直水面向下。o-xyz是以船舶重心为中心的附体坐标系，o-x轴为船体轴线上，方向由船艉指向船头，o-y轴指向右舷，o-z轴指向水面。为了便于分析航向角ψ与舵角δ之间的关系，在满足研究要求的前提下，可以忽略横摇、纵摇、垂荡的运动，只考虑横荡、前进、艏摇运动，将帆船运动简化为三自由度的数学运动模型［10-11］。

表1 无人帆船模型主尺度Table 1 The main dimensions of small autonomous sailboat model

图1 船体坐标系Fig.1 The coordinate system of hull

1.3 Nomoto 运动数学模型

根据牛顿关于质心运动的动量和动量矩定理，结合坐标系和速度转换关系，建立无人帆船在静水中的三自由度数学运动模型［12-13］：

式中：m 为船的总质量；uG，vG，u̇G，v̇G分别为重心处前进和侧向速度，以及其对时间的导数；r，ṙ分别为艏摇角速率及其对时间的导数；Fx，Fy，Mz分别为在x，y，z轴重心处作用的外力和外力矩；IzG为船舶绕轴z0的转动惯量。再从控制工程的角度出发，考虑船体艏摇角的变化与舵角运动的关系，根据帆船的水动力学模型和输出方程，将式（1）的三自由度状态空间方程转化为传递函数表达式，简化得到著名的Nomoto 数学模型：

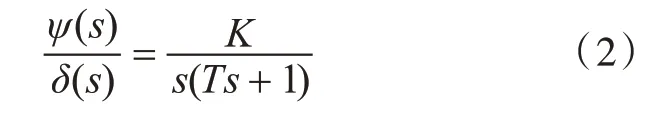
式中：回转性参数K 和稳定性参数T 分别为操舵后的角速度和达到最高旋回角速度所需时间；s为拉普拉斯变换因子。

1.4 舵机数学模型

舵机在实际控制过程中具有一定的延迟效应，在某种程度上会影响到航向控制的精确性，一般可以将舵机看作一阶惯性环节［14］：

式中：δc为目标舵角；T0为舵机的时间常数，一般取1～3 s，本文仿真中取T0=1。

2 无人帆船航向控制方法

不同特性的帆船在海上航行时会有不同的禁航区域，一般认为此区域在逆风30°～45°之间，此时，需要采用Z 型抢风航行，除此外，帆船可以实现任意航向的航行［15］。而在具体的直航段，无人帆船的航向控制方法会有所不同，其控制效果也会有明显的差异。为了实现响应快和稳性高的航向控制，本文采用了模糊PID 控制法。

2.1 模糊PID 控制器设计

传统PID 算法对航向进行控制时，以给定的目标航向角ψc与当前实际航向角ψ的偏差e作为控制器的输入，以舵角值δ作为输出。模糊控制器对于某一给定的航向角，会不断地根据偏差e和偏差率ec，通过制定的模糊规则，输出Kp，Ki，Kd的值，然后与原PID 值进行并联控制，输出目标舵角δc，再经过舵机系统，对被控对象输入确定的舵角值。如此循环，不停地调节帆船的航向，直至实际航向角与目标航向在预期的误差范围内，并达到稳定的动态控制状态。控制器的整体控制流程如图2 所示。

图2 模糊PID 控制系统Fig.2 Fuzzy PID control system

目前，模糊控制和PID 控制相结合的方式主要有：相互切换型控制、并联混合型控制和参数整定型控制。相互切换型控制方法一般是在较大误差范围内选用模糊控制，较小误差范围内转化为PID 控制；并联混合型控制方法是根据PID 整定的参数加上模糊控制的参数，并联进行控制；参数整定型控制方法是利用模糊控制器，根据模糊规则，通过在线整定PID 参数来控制。由于并联混合型控制较灵活，本文采用此种方式。

2.2 模糊控制规则设计

本文采用的模糊控制规则，主要是根据PID整定的专家经验：当偏差e较大时，为了使系统具有较好的追踪反应性能，避免出现较大的超调量，应取较大的Kp和较小的Kd，Ki值；当偏差e中等时，为了具有较小超调量和缓和的系统响应，应取较小的Kp和适中的Kd，Ki值；当偏差e较小时，为使系统具有较好的稳定性能，防止系统在设定值附近出现波动，应取较大的Kp，Ki值；当偏差率ec较大时，取较小的Kd值，通常情况下Kd为适中值。通过实际调整的过程，制定了如表2所示的49 条规则。其中，模糊控制的输入e，ec和输出Kp，Ki，Kd的7 个论域范围均为（-1，1），其模糊子集均为NB，NM，NS，ZE，PS，PM，PB，分别代表负大、负中、负小、零、正小、正中、正大。

在仿真过程中，先将输入量e，ec做归一化处理，再将输出Kp，Ki，Kd按照PID 控制范围加入适当的增益。e，ec的变量子集区间如图3（a）所示，隶属函数为smf，zmf 和trimf；Kp，Ki，Kd的变量子集区间如图3（b）所示，隶属函数为trimf。同时，采用Mamdani 的模糊控制方法，变量子集的模糊交、或、推理、聚类输出、反模糊化方法分别为“min”，“max”，“min”，“max”，“centroid”。

表2 Kp，Ki，Kd 模糊控制规则Table 2 Fuzzy control rules for Kp，Ki and Kd

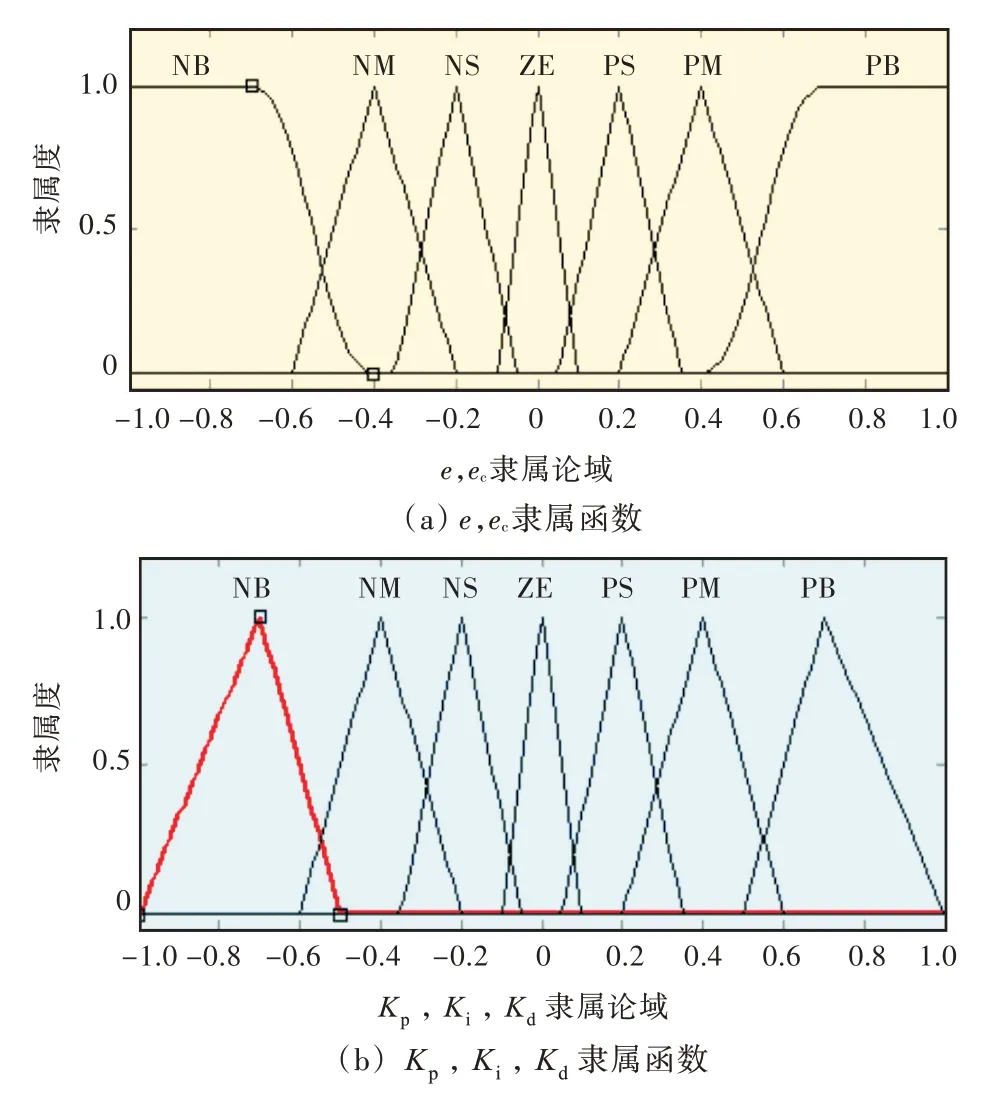
图3 模糊变量子集Fig.3 Fuzzy variable subset

2.3 控制器仿真模型搭建

借助Matlab 的Simulink 仿真工具，根据PID 的控制原理和图2 设计的模糊PID 控制器，搭建了如图4（a）所示的传统PID 控制仿真模型，和图4（b）所示的模糊PID 控制仿真模型。其控制过程如图5 所示。首先，根据设定的目标航向角与当前的实际航向角对比，计算出偏差和偏差率，判断帆船是否处于目标航向，若出现偏航，则控制器通过对舵的调整来进行航向控制，最终达到目标航向。其中，模糊PID 中的并联混合控制器在运行时会不断检测e与ec，通过制定的模糊规则并利用模糊推理的方法，在线实时生成控制器的3 个控制参数，再与设定的固定PID 参数值叠加进行舵角的控制，从而实现航向的控制。

帆船的实际航向除了受到舵的主要控制外，还会受到风、帆、浪、流等因素的干扰影响，而这些影响因素往往表现出很强的非线性和时变性，难以提前预测和建立准确的数学模型。这些未知因素最终会对帆船的航向造成影响，出现一定的偏航现象。在仿真模型中，加上特定范围内的随机干扰模块，每0.5 s 产生-4～4 之间的随机数。同时，也加入了舵角监测模块，由此可以检验控制器的控制方法是否具有较好的动态控制性能。

3 仿真分析与试验对比

3.1 仿真分析

本文以实尺度的帆船模型进行仿真模拟研究。假设船的初始航向角和舵角值均为0，设定目标航向角ψc=120°，处于非逆风航行区域，根据理 论 计 算 公 式：Kp=T⋅Wn

图4 控制器仿真模型Fig.4 Controller simulation model

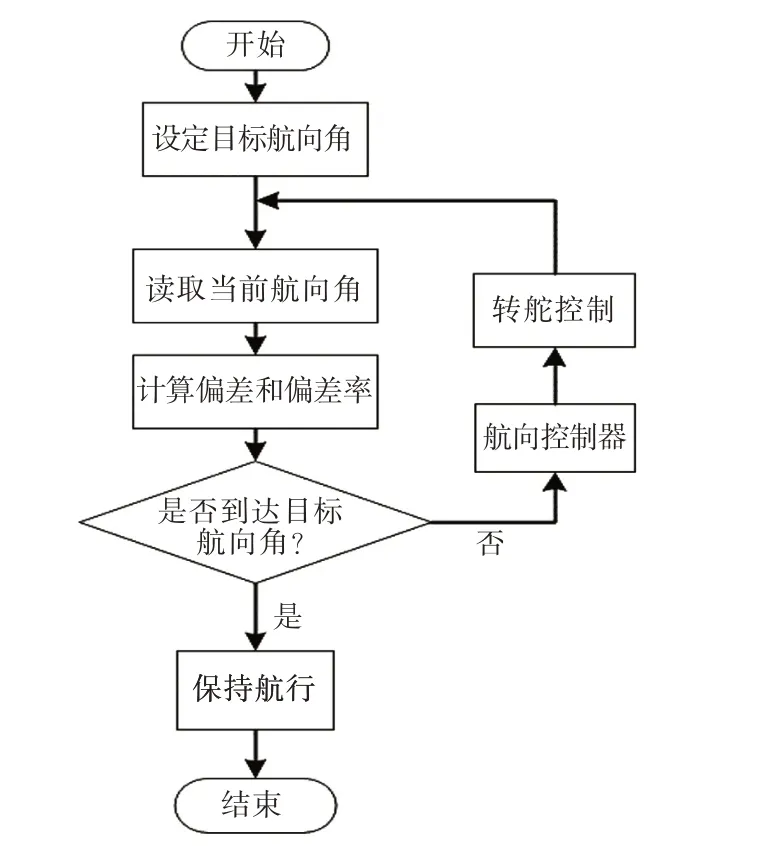
图5 控制流程图Fig.5 Control flow chart

2/K，Ki=T⋅Wn3/K，Kd=(2T⋅ε⋅Wn2-1)/K，其中Wn，ε分别为系统的自然频率和相对衰减系数。适当修改得出PID 控制参数Kp=0.42，Ki=0.001，Kd=1.12。由于航速不同，帆船的回转性参数K 和稳定性参数T 也会有所不同，当航速V 分别为2.0，2.5 和3.0 m/s 时，回 转 性 参 数 分 别 为-21.99，-27.49，-32.98，稳定性参数分别为-22.96，-18.36，-15.30。

不同航速下，2 种控制仿真对比结果如图6 所示。从图中可以看出，这2 种控制方法均能实现航向的控制，但控制效果有所差别。当航速V=2.0 m/s 时，传统PID 控制在3 s 左右达到目标航向角，并出现了20°左右的最大超调量，在10 s 左右趋于稳定；模糊PID 控制的调节时间约为6 s，无超调量。当航速V=2.5 m/s 时，传统PID 稳定控制时间约为9 s，最大超调量为10°；模糊PID 控制调节时间约为7 s，无超调量。当航速V=3.0 m/s 时，传统PID 控制调节时间约为12 s，最大超调量为5°，并出现了一定的波动情况；模糊PID 控制调节时间约为6 s，无超调量。

图6 两种控制方法的仿真对比Fig.6 Simulation comparison of two control methods

传统PID 控制和模糊PID 控制的主要控制性能参数如表3 所示。从表中可以看出，模糊PID 和传统PID 相比有较短的稳定调节时间和更小的操舵角，且均未出现明显的超调量和波动情况。由于传统PID 参数固定，往往是在船舶到达目标航向角并出现一定的超调和偏差后，才进行转舵的控制。而模糊PID 能够动态调节参数，在即将到达目标航向角时提前进行转舵的控制，使其在面对不同的航速和复杂的海洋环境干扰下，表现出很好的控制效果和较强的自适应能力。

表3 传统PID 与模糊PID 控制对比Table 3 Comparison between traditional PID and fuzzy PID control

3.2 试验对比

本次试验的船体结构如图7 所示，使用的控制板有主控板和驱动板，配备的传感器主要有超声波风速风向仪、帆角编码器、电子罗盘、GPS 和温湿度变送器，执行机构有转帆的无刷直流电机和操舵的电动推拉杆，不同距离分别采用GPRS与2.4 GHz 无线通信。地面基站处，无人帆船监控软件监视实时返回的数据和控制数据。无人帆船监控软件是使用Visual Studio 软件编写的MFC 应用程序，可实时监控船舶状态、修改参数、记录数据文件等。该执行信号由基站通过Modbus 传输至船载主控模块，再将控制信号通过CAN 总线传输到驱动模块，实现对执行机构的控制。

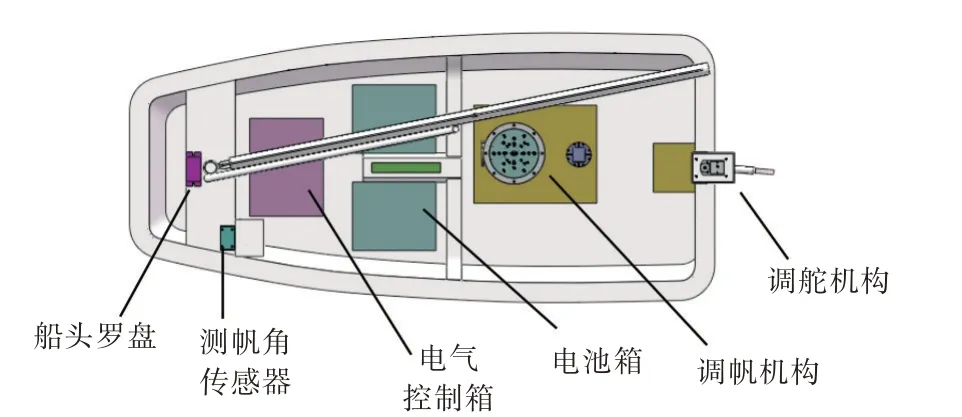
图7 船体结构Fig.7 Ship structure

试验过程中，通过电子罗盘实时检测帆船的航向角，并与设定的目标航向角进行比较，得出航向偏差作为控制器的输入，通过传统PID 或模糊PID 输出舵角值，对执行机构进行舵角的控制。试验时，设定目标航向角为25°，帆船航迹和航向角如图8（a）和图8（b）所示，分别运用传统PID 与模糊PID 这2 种方法对帆船给定航向进行控制，湖试情况如图8（c）所示。在较小的风、流干扰下，对处于非逆风航行的帆船，从试验数据对比结果可以看出，模糊PID 与传统PID 均能实现目标航向的控制，但传统PID 的轨迹偏差和航向角波动较大，而模糊PID 则能较快地到达目标航向角且较稳定。综合情况下，模糊PID 具有更好的航向控制效果。

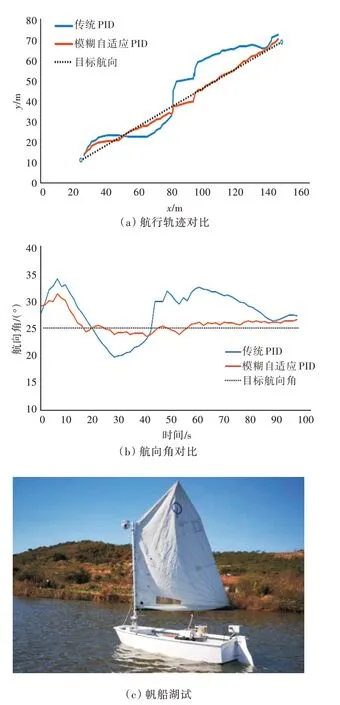
图8 试验对比结果Fig.8 Experimental comparison results

4 结 论

本文以自主设计的无人帆船模型为研究对象，根据帆船的实际特征参数建立运动数学模型，采用模糊PID 方法设计控制器，对帆船航向进行仿真控制研究，与传统PID 控制方法进行对比并进行了试验验证。

通过对航向控制仿真及试验结果分析发现，以不同的航速到达同一航向角，2 种针对帆船的控制方法实现情况有所差异。模糊PID 控制器具有较快的稳定调节时间，较小的超调量和操舵角，以及较强的抗干扰能力，能够实现对帆船航向的稳定控制。综合整体对比结果可知，基于模糊PID 的方法可以应用到小型无人帆船的航向控制，并且对于无人帆船的智能航向具有一定的参考价值。未来也可以应用该方法进一步考虑帆和舵的联动控制，考察其对帆船航向的影响和控制效果。