钢板组合梁桥面板横向计算分析研究

谢 银

(安徽省交通规划设计研究总院股份有限公司；公路交通节能环保技术交通运输行业研发中心，安徽 合肥 230088)

0 引 言

对于钢板组合梁桥，混凝土桥面板在纵桥向与钢梁形成组合结构共同受力，同时在横桥向又要收到桥面板自重、二期铺装、车辆等荷载的横桥向作用，以及车辆偏载时纵梁挠度差产生的扭转作用。该扭转作用一般在跨中位置最大，原因是跨中位置支座约束效果最弱，纵梁挠度差值最大。

扭转作用难以准确计算而且在常规纵梁间距的情况下，扭转效应占比很小，在设计时通常留有富裕度，以考虑扭转的影响。

本文重点研究在恒载及车辆荷载作用下，桥面板的边界条件对横向计算结果的影响。计算时将桥面板支承处简单地按铰接处理会发现正弯矩较大，而最大正弯矩处截面没有加厚，一般只有25 cm左右，在双主梁间距达到6 m以上时，底部计算配筋往往很大。如若将桥面板支承处按固接处理会发现正弯矩很小，只有铰接的1/5左右。显然钢板组合梁对桥面板的支承达不到固接的程度，按固接计算结果不安全。我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)在计算与梁肋整体连接的板的弯矩时支点截面偏安全地按固端考虑，跨中截面偏安全地按弹性半固结考虑。因此钢板组合梁桥面板也应该按照弹性半固结考虑，达到既经济又安全的效果。

本文通过12.65 m宽桥面板横向计算，研究桥面板边界条件对桥面板横向弯矩效应的影响。

1 桥面板构造

混凝土桥面板采用C50混凝土，板宽12.65 m，上铺8 cm厚C40防水混凝土+10 cm厚沥青混凝土，支承于两道钢板梁上，钢板梁横向等间距6.65 m。钢板梁上设置剪力钉，桥面板通过剪力钉与钢梁相连形成整体。桥面板标准厚度25 cm，支承处加厚至40 cm；每隔60 cm布置一道BM15-4横向预应力。计算模型如图1所示。

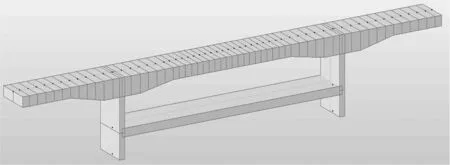
图1 计算模型示意图

选取跨中标准段1 m建立计算模型。为考虑钢梁对桥面板的弹性约束作用，用无重力混凝土竖向立柱模拟纵梁竖向加劲肋，无重力混凝土横梁模拟小横梁。模拟原则为每米截面惯性矩相同。

2 桥面板荷载

桥面板重度采用26.0 kN/m3，护栏自重取10.0 kN/m，二期铺装荷载取4.6 kN/m2。荷载加载方式如图2所示。

图2 二期铺装荷载示意图

3 车辆荷载有效分布系数

汽车的轮胎压力作用在桥面板上之后会沿着桥面板传递给钢梁，在横向传递过程中，应力发生扩散。假如轮胎的直接作用长度为1 m，那么传到钢梁上之后，承担该荷载的钢梁长度必然大于1 m，也就是说桥面板的有效宽度大于1 m。我们建立计算模型时如若将桥面板做成变宽的，建模过程就非常费时费力。因此我们在建立模型时一般将桥面板建成等宽的，反过来将荷载进行折减，该折减系数即为有效分布系数。

有效分布系数 =1/有效分布宽度

本文通过我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)的规定计算桥面板有效分布宽度。有效分布系数计算结果如图3所示。

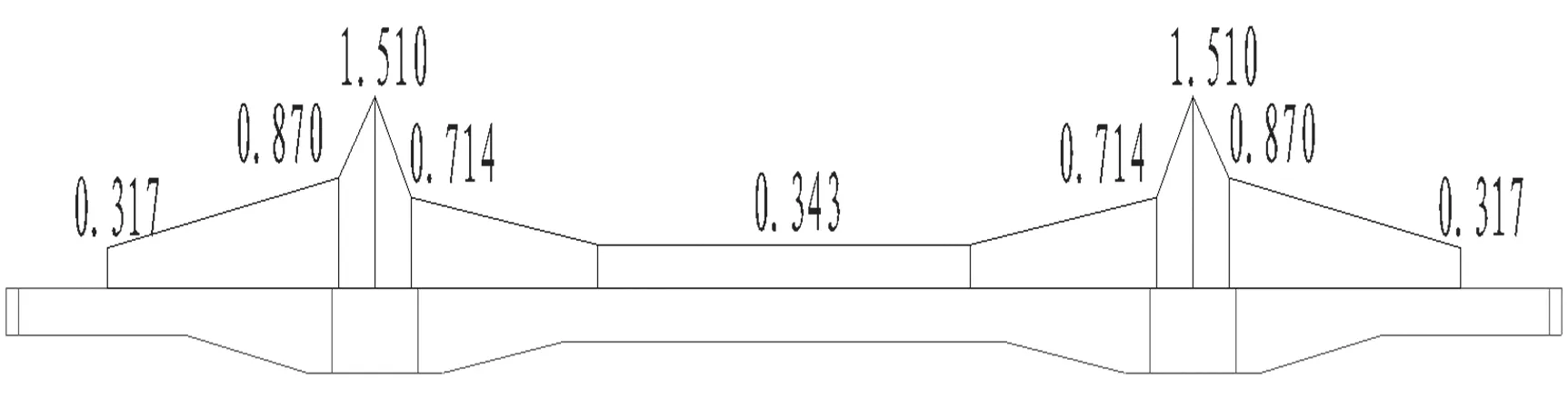
图3 桥面板有效分布系数

4 计算结果

4.1 弹性模型与固接和铰接模型计算结果对比

(1)车辆荷载下弯矩:见表1。

表1 车辆荷载作用下桥面板弯矩表

(2)基本组合下弯矩：见表2。

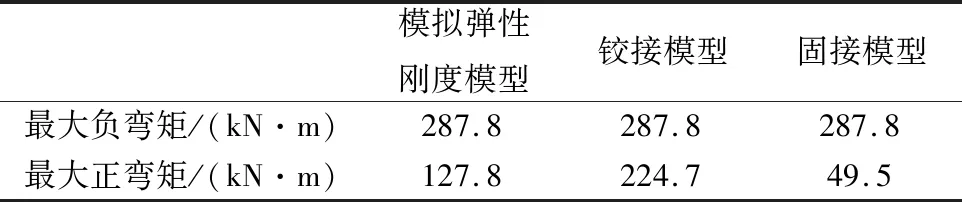
表2 基本组合下桥面板内力表

通过表1、表2三个模型结果的数据对比可以发现：

(1)负弯矩值不受边界条件影响。本案例悬臂3 m较大，因此最大负弯矩由悬臂部分的静定结构控制，不受边界条件影响。悬臂长度与双主梁间距比值为0.45，该比值减小到一定程度时，最大负弯矩将由双主梁之间的荷载控制，届时三个模型的结果将不会保持一致。

(2)最大正弯矩值相差较大，铰接模型与固接模型的值相差354%。最大正弯矩值对边界条件较为敏感，模拟弹性刚度模型的计算结果在两者之间，约为铰接模型的57%，小于公路混规的建议值(70%)。

4.2 模拟纵梁刚度对正弯矩的影响(表3)

表3 最大正弯矩-纵梁刚度表

由表3可以看出，纵梁刚度对最大正弯矩的影响随着刚度的增加，变化率越来越小，迅速衰减。最大正弯矩收敛于60 kN·m左右，约为固接模型的2倍。

4.3 模拟横梁刚度对正弯矩的影响(表4)

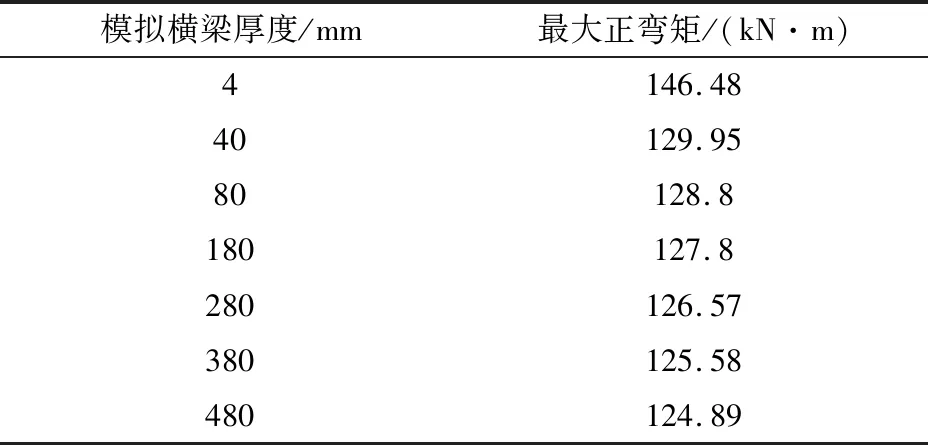
表4 最大正弯矩-横梁刚度表

由表4可以看出，横梁刚度对最大正弯矩影响较小，影响值在5%以内。但是小横梁的存在与否对弯矩的影响不可忽视。

5 结 论

通过对12.65 m宽双主梁桥面板在不同的边界条件下的横向计算可以得出以下结论:

(1) 一般情况下，最大负弯矩由悬臂静定结构控制，不受边界条件影响。

(2) 铰接模型的最大正弯矩偏保守，计算配筋值偏大；固接模型最大正弯矩偏不安全。

(3) 加劲肋刚度及间距对最大正弯矩影响较大，但增加加劲肋刚度效果迅速衰减，最大正弯矩最终收敛值仍大于固接模型结果。

(4) 小横梁刚度对最大正弯矩影响很小，但是小横梁的存在与否对计算结果影响不容忽视。

在工程应用中，采用铰接模型计算简便，安全度可以保证，但是配筋偏大，不经济。在纵梁间距较小时横向配筋为构造配筋，可采用铰接模型。在纵梁间距较大时，宜采用模拟弹性刚度模型。