临界阻尼状态下局部导电体TEM观测电压表达式的探讨
高 正,李文尧, 熊彩云
(昆明理工大学 国土资源工程学院,昆明 650093)
0 引言
瞬变电磁法(TEM)具有穿透能力强、探测深度大、适应环境能力强、应用领域广、应用效果好等优点[1],因此在国、内外广泛应用于地质调查[2]、资源勘查[3]、工程地质[4]、水文地质[5]、环境地质等领域[6]。临界阻尼状态下局部导电体观测电压表达式对研究局部导电体在接收线圈上感应电压的衰减特征和接收线圈的响应特性有重要的参考价值,在研究过程中发现,临界阻尼状态下局部导电体观测电压表达式存在两种不同的推导结果,一种可在文献[7-17]中查得,另外一种可在文献[18-19]中查得,两种表达式存在一个符号差异。为了探究原因,笔者对临界阻尼状态下局部导电体观测电压表达式重新进行了推导。
1 电压表达式
1.1 表达式推导
临界阻尼状态下局部导电体观测电压表达式存在两种不同的结果,文献[7-17]中的表达式为:
(1)
式中:
B=δ2+2δ/τ+1/τ2
(2)
(3)
A是和地质体有关的常数;L为接收线圈电感;C为接收线圈分布电容;R为接收线圈匹配电阻;t为观测时间;Vc为观测电压;τ为确定Vc(t)衰减速度的特性参数,称为时间常数。
文献[18-19]中的表达式为:
(4)
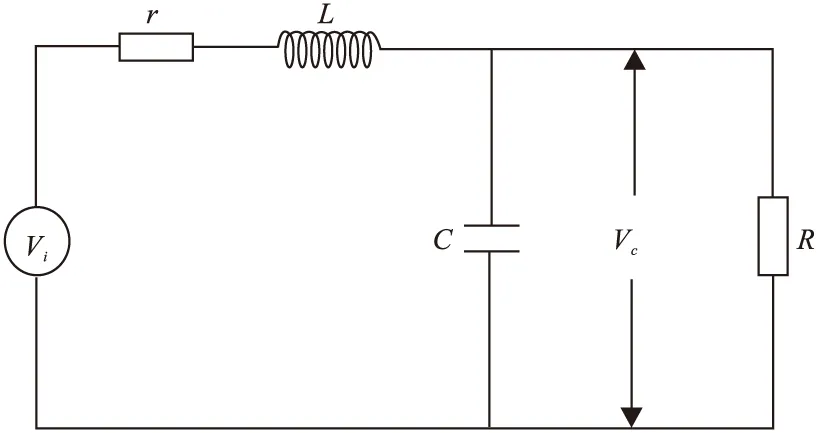
图1 接收线圈等效电路图
式中
B=δ2-2δ/τ+1/τ2
(5)
由于式(2)和式(5)存在一个正负号差异,为了验证式(2)与式(5)的正确,笔者查阅了大量国内、外文献,没有查到关于该表达式完整的推导过程,因此对临界阻尼状态下局部导电体观测电压表达式进行重新推导。
TEM接收线圈等效电路由内阻、电感、分布电容、匹配电阻构成。等效电路图如图1所示,电路图中,Vi为地下地质体在接收线圈上的感应电压,Vc为观测电压,r为线圈内阻,L为线圈电感,C为分布电容,R为匹配电阻。
在电容支路中
(6)
(7)
(8)
对于图1的等效电路,根据基尔霍夫定律得
Vi=Vr+VL+Vc
(9)
则由式(7)、式(8)、式(9)可得
(10)
式中
(11)
(12)
当t=0时,Vi=0,iL(0-)=iL(0+),电感电流不能突变,电感等效于开路,电容电压不能突变,电容等效于短路。因此初始条件为:
Vc(0)=0
(13)
(14)
当Vi=0时,式(10)的特征方程为:
(15)
当线圈工作在临界阻尼(δ=ωp)情况下,特征方程15)的两个根分别为:
当δ=ωp时,t1=t2=-δ,则Vi=0时齐次方程(10)的通解为:
Vc=(c1+c2t)e-δt
(16)
当t≥tof时,局部导电体在接收线圈上的感应电压[8]
(17)
令
(18)
则当t≥tof时,
Vi=Ae-t/τ
(19)
对于非齐次方程式10),可写成[8,15,19]
(20)
λ=-1/τ不是特征方程的根,设非齐次方程(20)的一个特解为b1则
Vc=b1e-t/τ
(21)
(22)
(23)
将式(21)、式(22)、式(23)代入式(20)得
(24)
则
(25)
故通解为
(26)
则
(27)
由式(13)、式(26)得
(28)
由式(14)、式27)得
(29)
故
(30)
整理得
(31)
令
(32)
则式31)可写成
(33)
1.2 MATLAB软件验证推导结果
用MATLAB求式20)中Vc表达式的程序如下:
dsolve('D2v+2*a*Dv+a^2*v-c*exp(-t/d)','Dv(0)=0','v(0)=0','t')
输出结果为:
ans =
(c*d*t*exp(-t/d))/(a*d - 1)- (c*d*t *exp(-a*t))/(a*d - 1)- (c*d^2* exp(-a*t))/(a*d - 1)^2 + (c*d*exp(a*t - t/d)*exp(-a*t)*(d + t - a*d*t))/(a*d - 1)^2
式中:
整理得Vc表达式为:
(34)
令
(35)
则式34)可写成
(36)
由MATLAB软件推导的式(35)、式(36)可知,本文推导的式(32)、式(33)是正确的,本文推导的结果与文献[18-19]中的表达式式(4)、式(5)一致,所以文献[7-17]中的式(1)、式(2)是错误的。
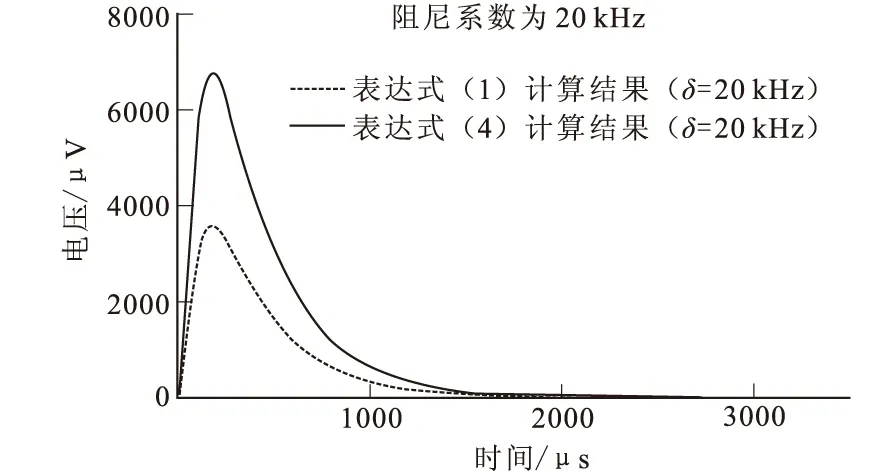
图2 阻尼系数为20 kHz时计算结果对比图
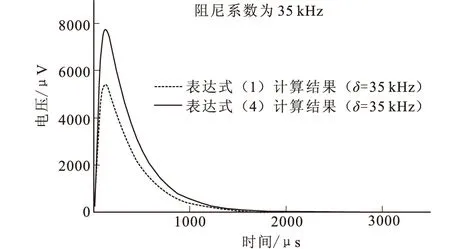
图3 阻尼系数为35 kHz时计算结果对比图
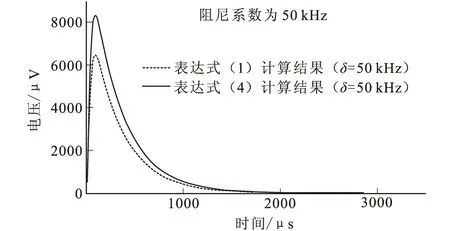
图4 阻尼系数为50 kHz时计算结果对比图
2 表达式(1)的误差分析
由于式(1)被大量文献引用,因此笔者对表达式(1)计算结果的影响进行研究。由式(2)和式(5)可知,线圈阻尼系数δ和时间常数τ是导致表达式(1)和表达式(4)出现差异的两个因素,因此对δ和τ对表达式计算结果的影响进行探讨。
2.1 线圈阻尼系数δ的影响
设定相关参数的值,并将其分别代入到式(1)、式(4)中,通过计算发现,当时间常数τ的值一定时,随着阻尼系数的减小,式(1)的计算结果与式(4)的计算结果相比,式(1)计算的误差越来越大。当阻尼系数在20 kHz~50 kHz(常用小线圈阻尼系数范围[20])用式(1)计算的观测电压误差达22 %~46 %,详细计算结果见图2、图3、图4,不同阻尼系数情况下用式(1)计算的观测电压相对误差如表1所示。
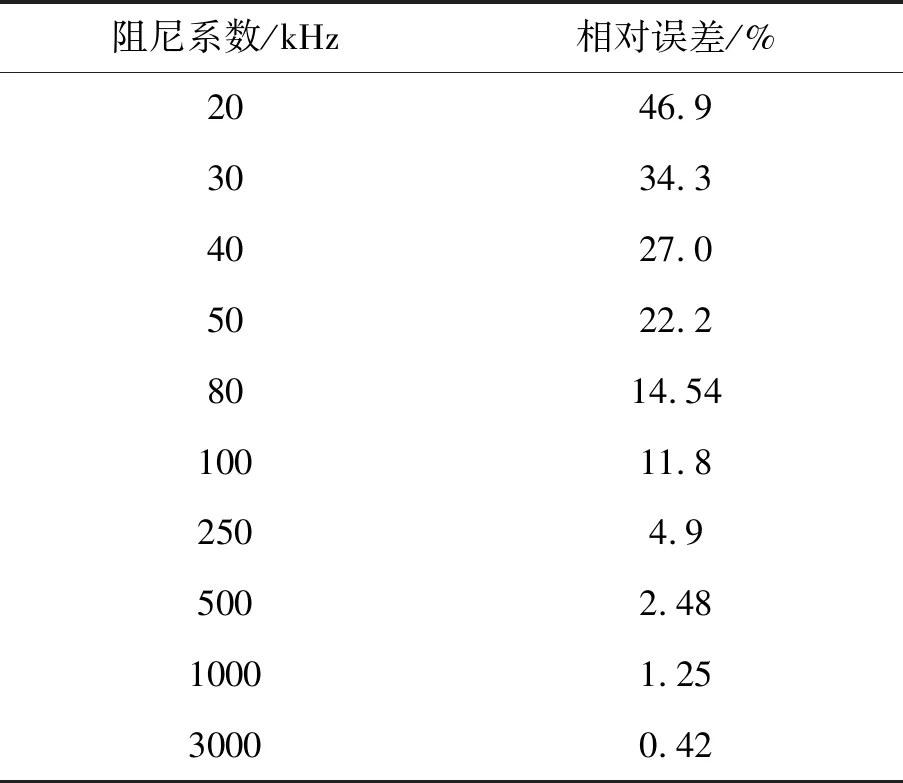
表1 式(1)计算结果相对误差
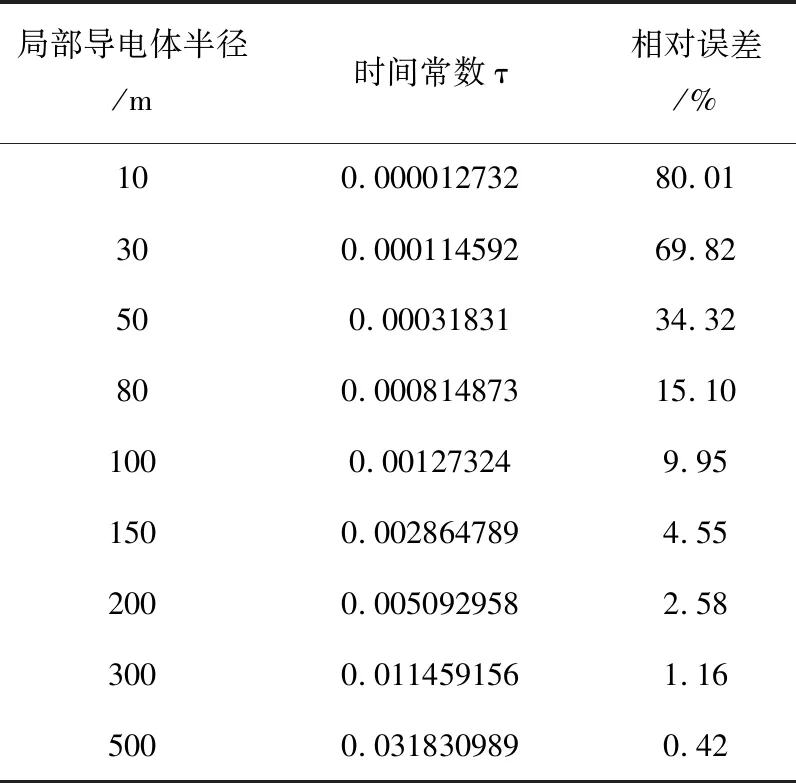
表2 式(1)计算结果相对误差(δ=30 kHz)
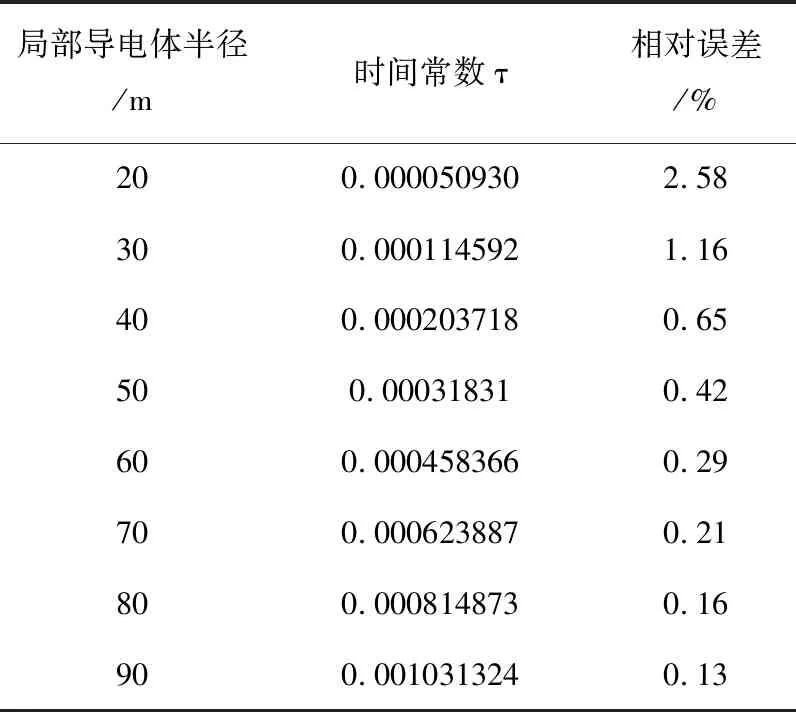
表3 式(1)计算结果相对误差(δ=3 000 kHz)
由图2、图3、图4可知,式(1)和式(4)计算的观测电压曲线形态相似,但是用式(1)计算的观测电压值偏低。
由表1可知,随着阻尼系数的减小,用式(1)计算的观测电压的误差越来越大。
2.2 时间常数τ的影响
时间常数τ的表达式为[8]:
τ=μ0σa2/π
(37)
式中,μ0=4π×10-7H/m为空气磁导率,σ为电导率,a为局部导电体的半径。
由于要研究当时间常数τ变化时,式(1)的计算结果与式(4)相比的误差,且时间常数τ与局部导电体半径呈正相关,所以取电导率σ为1 S/m,通过变化局部导电体半径a的值来展开探讨。
当阻尼系数一定时,不断变化局部导电体半径,式1)计算的观测电压值的误差如表2、表3所示。
由表2、表3可知,当阻尼系数一定时,随着时间常数τ的值的减小,表达式(1)计算的观测电压误差越大。
3 结论
通过验证式(1)是错误的,不建议使用,式(4)是正确的,建议使用;式(1)和式(4)计算的观测电压曲线形态相似;当时间常数一定时,随着阻尼系数的减小,式(1)计算的观测电压误差越来越大;当阻尼系数一定时,随着时间常数的减小,式(1)计算的观测电压误差越来越大。

