基于粒子群算法的GPR与电测深共同反演及等值现象消除

戴前伟，张 豪，张 彬

(1.中南大学 地球科学与信息物理学院，长沙 410083；2.中南大学 有色金属成矿预测与地质环境监测教育部重点实验室，长沙 410083)

0 引言

在地球物理勘探中，以岩矿石间导电性的差异为基础，通过观测和研究人工电场的地下分布特点，来解决实际问题的电阻率法是电法勘探的一个重要分支，电阻率ρ是描述导电性强弱的电性参数。在实际的工作中，不可避免的会存在着一定的观测误差，从而使得不同的地电断面所对应的电测深曲线之间出现等值现象，造成错误的解释。而探地雷达则是根据高频电磁波在地下介质中的传播特性，探测地下结构和特性的一种地球物理方法。依照电磁场与电磁波理论，介质的介电常数、电导率和磁导率的差异决定了电磁波的穿透深度、传播路径、波形以及发生反射、绕射现象等。因此，探地雷达的勘探结果不会出现等值现象。

绝大多数的地球物理反演问题为非线性问题[1-2]，完全非线性反演的各类方法仍在不断地更新和发展。粒子群优化算法(Particle Swarm Optimization, PSO)是由Eberhart和Kennedy[3-5]通过研究鸟群社会系统，提出的一种基于迭代的群智能随机优化算法。算法的基本概念源于对鸟群觅食过程中的迁徙和集聚行为的研究。近年来粒子群反演越来越多的应用于地球物理领域。韩家兴[6]提出了基于粒子群优化算法的多元线性拟合法；孙中科[7]进行了重力张量的粒子群反演研究；张进[8]提出了加入模拟退火算子的随机粒子群算法用于反演弹性阻抗；罗德相[9]提出了多种群粒子群优化算法；易远元等[10]以地震波阻抗数值模拟和实际资料为例，说明了粒子群反演方法的可行性及有效性。

一条n层电测深曲线，可能对应一组不同参数(ρ,h)的n层地电断面，称为同层等值现象。它包括S等值和T等值两类[11]。为了解决电法勘探的S等值现象，笔者提出一种改进的多种群粒子群反演算法，在原有的速度更新公式的基础上，增加一个新的全局极值点，实现电法参数和探地雷达参数的共同反演，得到更加准确的地电模型。

1 同层等值现象

根据势场问题解的唯一性定理，一定的地电断面对应唯一的电测深曲线[12]。而实际工作中，当有些不同地电断面所对应的电测深曲线间的差别在观测误差范围以内，常将其看成为“同一条”电测深曲线，这种情况称为电测深曲线的等值现象。等值现象的存在，使得一条实测电测深曲线可对应一组不同的地电断面，从而造成错误的解释。

电法勘探的同层等值现象包括S等值和T等值两类。本次实验的重点在于解决S等值现象。因为电性层参数决定着电阻率转换函数，相同转换函数的地电断面对应着相同的电测深曲线，所以可以对转换函数的等值性进行分析，研究S等值现象的原因。

以三层曲线为例，对于H型和A型三层介质，各层电阻率为ρ1、ρ2、ρ3,层厚度为h1、h2、h3，电阻率转换函数T1(m)可表示为

T1(m)=ρ1cth{mh1+cth-1[μ2·

cth(mh1v2+cth-1μ3)]}

(1)

v2=h2/h1

(2)

μ2=ρ2/ρ1

(3)

μ3=ρ3/ρ2

(4)

其中：cth(x)为双曲函数中的余切双曲函数。当v2≪1，且μ3≫1，即第二层的层厚度小且第三层电阻率值远大于第二层电阻率时

(5)

(6)

故

(7)

由此可见，第二层厚度或电阻率发生改变时，只要S2=h2/ρ2保持不变，则T1(m)不变，故称为S等值现象。从前面分析可知，发生S等值现象的条件是：v2≪1即第二层薄，且μ3≫1。中间层越薄，ρ2越小等值范围越宽。

2 粒子群算法

2.1 标准PSO算法

(8)

(9)

解空间规定了粒子飞行的范围，在每次迭代中，粒子通过速度与位置公式不断进行着更新。粒子的速度更新公式分为三部分，①表示粒子当前的飞行速度，提供粒子在搜索空间中飞行的动力；②被称为“个体认知”部分，代表了粒子的个体经验，促使粒子朝着自身所经历过的最优位置移动；③被称为“群体认知”部分，代表了群体经验对粒子飞行轨迹的影响，促使粒子朝着目前群体发现的最优位置移动。

2.2 线性调整w的策略

线性调整w的算法，又称为惯性权重线性递减算法[14]。使用该算法对问题进行优化处理时，初始采用全局搜索，使搜索空间快速收敛于某一区域，之后采用局部精细搜索，可以求得更高精度的解。在vi前乘以惯性权重w，w较大时，算法具有较强的全局搜索能力；w较小，算法倾向于局部搜索。w调整公式为式(10)。

(10)

其中：wmax、wmin分别是w的最大值和最小值；iter和itermax分别是当前迭代次数和最大迭代次数。

2.3 多种群粒子群优化算法

多种群粒子群优化算法与标准粒子群优化算法的区别在于，速度更新公式中，除了当前速度、“个体认知”和“群体认知”外，再增加一个不同约束条件下的“群体认知”，以获得问题的最优解。速度更新公式为式(11)。

(11)

对于标准PSO易陷入局部极值的问题，多种群粒子群优化算法可以通过新的约束条件得到相同解空间下的新的群体最佳，跳出局部极值。以本次实验为例，速度公式中的gbest1是以电法勘探数据通过多种群粒子群反演得到的全局最佳，gbest2是以探地雷达数据通过标准粒子群反演得到的全局最佳。由于电法勘探存在着等值现象，而探地雷达反演并不受其影响，因此gbest2可以准确地反演出层厚度参数，在迭代过程中可以有效的避免因等值现象而使结果陷入局部极值的情况。

3 实验算法流程

图1 算法流程图

本次实验过程中，电法勘探参数下的多种群粒子群反演作为反演主程序，通过探地雷达参数下的标准粒子群反演求得gbest2id，参与主程序反演。根据模拟探测地层的深度，探地雷达正演模拟采用一阶Mur吸收边界的FDTD算法[15-19]，方式为位于地表的自激自收，激励源采用主频为100 MHz的布莱克曼-哈里斯脉冲。由于参数维度的不同，我们对电法勘探模型参数和探地雷达模型参数进行处理，将两种勘探方法所得到的参数分为电性参数和几何参数。以n层地电断面为例，对电法勘探参数和探地雷达参数进行处理：电法参数model=(ρ1，ρ2，…，ρn与h1，h2，…，hn-1),ρ1、ρ2、…、ρn称为电性参数ρs，h1、h2、…、hn-1称为层厚度参数h1。同理，探地雷达参数model=(ε1,ε2,…εn,σ1,σ2,…σn,h1,h2,…hn-1)，ε1、ε2、…、εn与σ1、σ2、…、σn称为电性参数εσ，h1、h2、…、hn-1称为h2。

运行反演主程序，当多种群粒子群反演算法进入迭代后，程序首先调用探地雷达参数下的粒子群反演程序，得到一组探地雷达模型参数下的速度v2id、位置x2id、个体极值点pbestid、全局极值点gbestid并返回给电法反演主程序。取此全局极值点中的层厚度h2，介电常数与电导率εσ，并用h2替换电法反演程序上次迭代(第一次为粒子初始化)所得的全局极值点中的层厚度h1，组成一个新的与电法勘探参数维度相同的全局极值点gbest2，并进行反演。一次迭代过后，得到新的vid、xid、gbest1id。取各个数组中的层厚度参数h1，并用h1替换探地雷达程序上次迭代所得对应数组中的层厚度h2，代入探地雷达粒子群反演程序，以此循环。

通过这种方式，层厚度参数在整个反演过程中不断进行着更新，矫正电法勘探因等值现象而出现的误差，得到更准确的地电模型。

表1 H型模型反演结果

4 算例分析

本次实验分析了水平地层上的H型和A型三层电测深曲线，曲线的基本形态由ρ1、ρ2、ρ3之间的大小关系决定。前两层厚度为h1、h2，第三层为无限大。

4.1 H型三层曲线

H型三层曲线的电阻率关系为ρ1>ρ2<ρ3，且要满足S等值现象的条件，因此给定理论模型model=(1 500，200，2 000，10，2)，分别进行标准粒子群反演和多种群粒子群反演，对实验结果进行分析。

用标准粒子群反演程序对理论模型进行反演，取连续三次的模拟结果，记为model1、model2和model3。反演过程中，粒子群个数M=50，学习因子c1=c2=1.496 2，wmax=0.9，wmin=0.4。在最大迭代次数itermax=50的情况下均可达到最大误差界限常数，记录反演结果

给定与理论模型相同的地电断面的探地雷达参数为model=(3，7，10，1/1500，1/200，1/2000，10，2)，其中第一层的相对介电常数ε1为3，电导率ρ1为1/1500；第二层的相对介电常数ε2为7，电导率ρ2为1/200；第三层的相对介电常数ε3为10，电导率ρ3为1/2000。用多种群粒子群反演程序进行反演，结果记为model4。两种反演算法的反演结果见表1，电法模型参数(即给定的理论模型)与反演结果对比见图2，各模型参数深度与视电阻率对比结果见图3。最后一次迭代后，探地雷达参数的模型参数与反演结果对比见图4。

图2 H型模型中模型参数与反演结果对比

图3 深度与视电阻率对比

由图4可见，从初始发射约116 ns第一层下底面反射波到达，151 ns第二层下底面反射波到达。其中，第一层单程走时为58 ns，电磁波速度为1.730 9×108m/s,相乘可得第一层层厚度为10.03 m; 第二层单程走时为18 ns，电磁波速度为1.133 1×108m/s,相乘可得第二层层厚度为19.83 m，与理论模型吻合，可以得到准确的层厚度参数。

对比表1和图1可以看出，在所给定的参数情况下，两种反演方法求得模型参数的正演响应曲线均与理论模型的正演曲线拟合，且都可以很好地求出ρ1、ρ3、h1的值。对比图2可以看出model1、model2和model3均出现了S等值现象，纵向电导S2=h2/ρ2≈100，第二层的电阻率ρ2和层厚度h2与理论模型model数据相比同倍数增大；model4与理论模型相比，未出现等值现象，反演结果较为理想。

表2 A型模型反演结果

图4 探地雷达参数的模型参数与反演结果对比

图5 A型模型中模型参数与反演结果对比

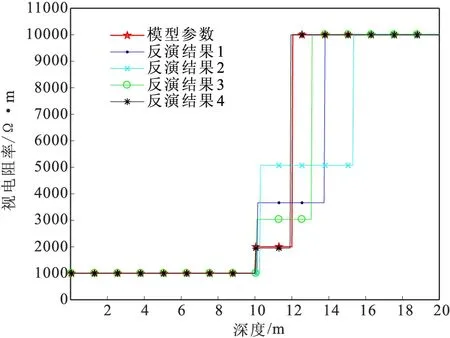
图6 深度与视电阻率对比图

4.2 A型三层曲线

A型三层曲线的电阻率关系ρ1<ρ2<ρ3，给定理论模型model=(1000，2000，10000，10，2)，用标准粒子群反演程序对理论模型进行反演，取连续三次的模拟结果，记为model1、model2和model3。粒子群反演各参数设置均与H型三层相同。给定与理论模型相同的地电断面的探地雷达参数为model=(3，7，10，1/1000，1/2000，1/10000，10，2)，用多种群粒子群反演程序进行反演，结果记为model4。两种反演算法的反演结果见表2，模型参数(即给定的理论模型)与反演结果对比见图5，各模型参数深度与视电阻率对比结果见图6。最后一次迭代后，探地雷达参数的模型参数与反演结果对比见图7。

图7 探地雷达参数的模型参数与反演结果对比

由图7可知，由于给出的H型和A型三层地电模型的层厚度、相对介电常数、探地雷达正反演程序的各参数均相同，所以A型模型的单程走时、电磁波速度等均与H型基本相同，探地雷达参数的最后一次粒子群反演迭代结果与理论模型吻合，可以得到准确的层厚度参数。

从表2和图5可以看出model1、model2和model3均出现了S等值现象，纵向电导S2=h2/ρ2≈300，第二层的电阻率和层厚度与理论模型model数据相比同倍数增大；model4与理论模型相比，未出现等值现象，反演结果较为理想。

5 结论

笔者改进了多种群粒子群反演算法，并将包含探地雷达信息的几何参数加载到算法中，为原算法增加一个新的全局极值点，实现电性参数和几何参数的共同反演，得到以下几点结论：

1)当理论模型或勘探结果满足S等值现象的发生条件时，用标准粒子群算法进行一维层状电法反演，容易陷入局部极值，出现等值现象，无法得到准确的地电模型。

2)多种群粒子群反演与标准粒子群反演相比，可以增加新的约束条件，不易陷入局部极值，取得更好的优化结果。探地雷达参数反演求得的第二个全局极值点，可以更好地求出层厚度参数。相比于电法参数的标准粒子群反演，在整个迭代过程中层厚度参数不断的进行着更新，在解空间内向着理论模型参数逼近，从而跳出局部极值点，避免了电法勘探的S等值现象。

3)多种群粒子群反演还有很多可以优化改进的地方，如c3的取值问题，c1、c2和c3之间的关系等还需进一步完善，如何解决T等值现象还需进一步改进。