龙门山地区介质密度的卫星重力数据反演

王毅鹏，张永志，韩 鸣，程 冬，槐岩柯

(长安大学 地质工程与测绘学院，西安 710054)

0 引言

长期以来，密度界面的反演是重力学研究的主要内容之一，研究龙门山地区地下介质密度结构对于分析该地区的地震活动具有重要意义。目前国内外研究地壳内部密度结构的方法主要有两种：①通过分析密度与速度的关系，将速度转化为密度[1]；②通过研究重力异常，反演地壳内部的密度界面。李媛等[2]使用地面实测重力数据，反演汶川地震之前龙门山地区地壳密度随深度的变化规律，经过分析得出该地区的介质密度随时间变化曲线显示为由突变到平缓，同时介质密度随地壳深度的增加变化特点明显；明圆圆等[3]利用鱼群算法进行密度异常的反演，当密度参数较少时，该算法效果明显，当密度参数较多时，则此算法使用受限；柯小平等[4]采用直立长方体模型结合遗传算法反演了青藏高原东缘的三维密度分布。此外，由于位场的可叠加性，导致重力反演结果具有不唯一性。为限制重力反演结果的随机性，加入地震测深数据约束是有效方法之一。唐新功等[5]在深地震测深数据资料约束下，使用GeoSoft软件反演龙门山地区的沉积层、康拉德界面和莫霍面的深度分布，研究表明龙门山地区在南北地震带两侧具有明显不同的地壳结构，该地区地壳的突变和不均匀性是导致地震活动强烈的主要原因之一。这些研究结果为分析龙门山地区近年来所发生地震的成因提供了一定的依据，然而由于地震研究的极端复杂性和以前研究中密度数据量不足、空间分辨率低等条件限制，以及存在计算方法复杂、速度慢的问题。高玮等[6]研究证明粒子群优化算法是研究地质力学参数反演的一种有效方法, 同时Parker[7]、Oldenburg(1974)[8]提出的Parker-Oldenburg频率域算法具有计算速度快速以及有效的特点；卢鹏羽等[9]将Parker-Oldenburg模型应用于重力张量数据的密度界面反演中，发现可以明显提高所反演密度界面的分辨率。因此笔者使用EIGEN-6C2超高阶卫星重力场模型，在频率域采用粒子群算法，反演龙门山地区的介质密度分布，并用于分析其地球物理学含义和研究。

1 Parker-Oldenburg频域反演方法

通常情况下，提高正演计算速度是改进反演速度的关键问题。Parker[7]提出了重力异常正演计算的频率域快速计算公式。Oldenburg[8]在Parker公式的基础上，采用FFT(快速傅里叶变换)提高正演的计算速度，同时使用低通滤波器来保证算法迭代的收敛性。由于FFT技术的使用，Parker-Oldenburg模型的计算速度得到了很大地提高，成为频域计算的主要方法。Parker-Oldenburg模型假设在x-z直角坐标系中，重力异常用Δg表示，场源层上部边界为z=0，下部边界为z=h(x)，此边界显示界面的起伏。

由EIGEN-6C2重力场模型所计算的重力异常经布格改正后可以得到布格重力异常，该重力异常归因于地表到地球深部所有因密度不均匀引起的重力效应的叠加，为了对地壳的密度分布特征进行研究，需要从布格重力异常中扣除地壳以下物质所引起的重力异常，由于莫霍面是地壳与地幔的分界面，因此也是密度发生突变的分界面。利用Parker频率域方法可以正演莫霍面起伏引起的重力异常，Parker频率域莫霍面起伏与地表重力异常关系为：

(1)

(2)

图1 异常场源坐标示意图

Parker-Oldenburg模型算法执行流程如下：

假定已知地层与下部介质间的密度差ρ，参考面深度z0已知或给定，则可以使用式(2)进行如下迭代计算：

1)给定界面起伏h(x)的初值。

2)将h(x)的初值代入公式(2)，计算该公式右端项的傅里叶变换。

3)式(2)右端项的傅里叶逆变换即为改进的界面起伏h(x)。

4)判断计算结果是否满足收敛标准，或达到给定的最大迭代次数。如果满足，则算法停止；否则转步骤2)，并以本次迭代结果作为初值，继续迭代计算。因重力异常的高频成分会导致反演结果不稳定，为保证算法迭代的收敛性，故对重力异常波数域的傅里叶变换结果进行低通滤波处理[9]。

(3)

其中:a、b为滤波参数；波数k=1/λ，波长λ的单位为km。

2 试验数据及处理方法

2.1 EIGEN-6C2超高阶卫星重力场模型

EIGEN-6C2重力场模型采用由地面重力数据、卫星测高数据、卫星重力数据联合解算，是GFZ(德国地学中心)在2012年发布的最高阶数达1949阶的重力场模型。李琦等[11]研究表明使用新的EIGEN-6C2重力场模型作为参考模型，最终解算所得的似大地水准面精度明显优于EGM2008模型所得解算结果,其精度甚至可以提高到3 cm。

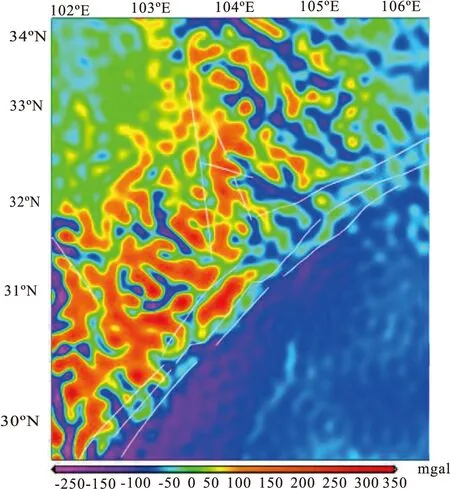
图2 龙门山地区自由空间重力异常

图3 龙门山地区布格重力异常

2.2 布格重力异常及处理

笔者利用EIGEN-6C2重力场模型计算得到龙门山区域的自由空间重力异常,然后依据Crust1.0所提供的中国大陆沉积层模型作沉积层校正和布格校正，则可得到布格重力异常，其中布格校正所用地形高程数据来自美国海洋研究所 (http://topex.ucsd.edu/cgi-bin/get_data.cgi)，空间分辨率为2 km。

我们根据已有的地球物理探测结果,在使用 Parker-Oldenburg模型反演时，假设初始界面的地壳厚度为0，基于Crust1.0地壳模型的计算结果，将龙门山地区及附近区域初始界面密度取为2.11 g/cm3，参考面深度取z0=45 km，密度差初值ρ=0.45 g/cm3，同时对重力异常数据使用边界锥形余弦滤波方法进行处理[10]，滤波参数值b=0.005,a=0.002 5，分别为滤波频率的上、下限值，经6次迭代计算后，MSE=0.275 4，最终得到龙门山地区的自由空间重力异常，如图2、图3所示。

由图2可知，龙门山地区自由空间重力异常变化剧烈，其变化范围为：-250 mGal～380 mGal，呈现出西北区域自由空间重力异常较高，东南区域自由空间重力异常较低，并自西向东逐渐减小，其原因可能与该地区地形的变化有密切联系。

由图3可知，该区域布格重力异常的变化范围为：-370 mGal～10 mGal，总体变化值较自由空间重力异常略低。西北区域布格重力异常低，东南区域布格重力异常则相对较高，同时布格重力异常值呈现自西向东逐渐增加的趋势；此外，由于川西高原的布格重力异常变化范围为：-370 mGal～-200 mGal；龙门山地区布格重力异常变化范围为：-200 mGal～-40 mGal；四川盆地布格重力异常变化范围为：-40mGal～-10 mGal,因此在龙门山地区附近形成了布格重力异常的高梯度带。

3 PSO算法

3.1 PSO算法原理

粒子群算法是人工智能群优化算法的一种,该算法在搜索寻找最优解的过程中可以将最优解保存，然后将最优解分配给下一次搜索的粒子，它通过追随当前的局部最优解来最终寻找到全局最优解；此外，粒子群算法由于具有收敛速度快、所需调整的参数少、计算复杂度低等优点被广泛应用于众多的科研领域[12]。

粒子群算法假设在D维搜索空间中，粒子的群体由n个粒子所组成，全部粒子在飞行中都具有确定的速度，Xi=(xi1,xi2,…,xiD)是第i个粒子的位置，Vi=(vi1,vi2,…,viD)是第i个粒子的飞行速度，pbesti=(pbesti1,pbesti2,…,pbestiD)是第i个粒子所能搜索到的局部最优位置，gbest=(gbest1,gbest2,…,gbestD)是整个粒子群所能搜索到的全局最优位置，同时在算法的每次迭代中，每个粒子使用式(3)和式(4)来更新其速度和位置：

(4)

(5)

(5)

其中:F是目标函数;Δg0为重力异常观测值；Δg为由密度参数所计算的重力异常值；N为观测点个数。粒子群优化算法执行的流程描述如下：

1)确定待反演参数的搜索区域，同时设置其上下边界，以及在搜索区域内随机产生一定数量的粒子，并且使每个粒子都具有随机的位置和速度。

2)使用所设计的目标函数F，计算每个粒子的最小适应值。

3)将每个粒子当前的局部最优适应值与已有全局适应值进行比对，如满足条件，则将其更新为当前粒子的最优适应值

4)继续将每个粒子的当前最优值与群体的最优值进行对比，并更新当前群体的全局最优适应值。

5)使用式(4)和式(5)迭代更新粒子的速度和位置。

6)使用已经更新过的粒子速度和位置继续计算目标函数，如果所得适应值满足算法的精度要求，则算法结束，否则转步骤2)继续执行算法。

3.2 粒子群算法反演结果

为验证本方法的有效性，我们使用粒子群算法反演计算龙门山地区介质的密度参数，反演区域为102°E～106°E和30°N～34°N，由于反演计算区域较大，故采用长方体剖分单元法，将研究区域划分成12′×12′共20×20个直立长方体进行计算,同时将每个长方体内部同一水平层的剩余密度设为常数，并与长方体高度(地壳厚度)成函数关系，各水平层的地壳密度可以由其剩余密度加上初始界面密度得到。由于计算数据量仍然较大，普通计算机无法完成运算，因此本文中的计算是在课题组内存为64GB的高性能服务器上进行PSO迭代运算，并对每次运算结果进行修正，以获得最优解，最终运行结果如表1，2所示，从以下两表可以看出，该方法能得到一个稳定的结果并接近真值。

表1 粒子群算法反演介质密度参数与真值

表2 粒子群算法反演参数及结果

表3 龙门山地区介质密度与Crust1.0对比

冯锐等[12]利用重力和地震资料，研究得出龙门山地区的地壳各层初始密度分别为：沉积层为2.3g/cm3、上地壳为2.67g/cm3、中地壳为2.80 g/cm3、下地壳为2.90 g/cm3[13-14]。本文以此为基础，并将反演结果与Crust1.0模型所得结果进行对比，结果如表3所示，以评估反演结果的正确性。

由表3可知，本文反演计算所得的结果与CRUST1.0模型值相比整体一致性较好[14]，但是反演结果显示上地壳、下地壳密度都略低于模型值，这可能是高频滤波时边界效应所导致的结果。

4 龙门山地区重力异常反演结果

4.1 莫霍面引起的重力异常及剩余重力异常

由图4可知，龙门山地区莫霍面起伏引起的重力异常总体变化值为：-420 mGal～160 mGal，重力异常自西向东逐渐增加，这与该区域的地壳厚度有较为密切的联系。通常地壳厚度越厚，莫霍面起伏引起的重力异常较低；地壳厚度越薄，则莫霍面起伏引起的重力异常较高。川西高原重力异常值为：-420 mGal～-320 mGal，龙门山地区重力异常为：-320 mGal～-200 mGal，四川盆地重力异常为：-200 mGal～-160 mGal，因此龙门山地区位于莫霍面起伏所引起的重力异常的高梯度带上，其两侧重力异常值之差达到了120 mGal。

图4 莫霍面起伏引起的重力异常

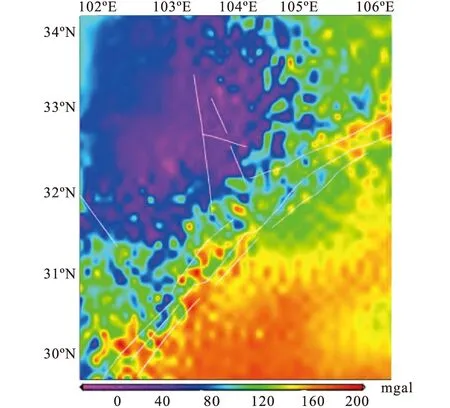
图5 剩余重力异常

图6 龙门山地区密度分布

龙门山地区的剩余重力异常，可以通过从区域布格重力异常中扣除莫霍面起伏所引起的重力异常而得到。因此由图5可知，该区域剩余重力异常自西向东逐渐增加，以龙门山地区为分界，西北区域剩余重力异常较低，说明该区域介质密度相对较小，这可能是青藏高原地下物质和能量的“东流”的结果；东南区域则剩余重力异常较高，说明该区域介质密度较大，这可能和四川盆地的克拉通地壳有关[15-16]。

4.2 地下介质密度

采用Parker-Oldenburg模型以及粒子群算法反演龙门山地区的地下介质密度结构，该区域地形起伏较大，包括川西高原、龙门山地区和四川盆地，反演所得介质密度分布如图6所示。

图6显示了龙门山地区密度分布随地壳深度变化的特征：整体而言，不同深度的密度分布与区域剩余重力异常呈现对应关系：高密度区对应的区域剩余重力异常高；低密度区对应的剩余重力异常低；不同深度层的介质密度均表现为西北区域低、东南区域高，并且表现出自西向东逐渐增加的特点；显示龙门山地区东西两侧密度差异较大；此外在图6中，深度为10 km～20 km和30 km～40 km的横向分辨率差异较小这可能是由于地下介质密度之间中间层的连续性所导致的结果，反映出该区域剧烈的地下构造运动特征[17]。龙门山地区地下介质密度值随深度变化对比关系如表4所示。

由表4分析可知，龙门山地区以及相邻区域不同深度的地壳密度分布各异，介质密度随深度加深而增加；在同一深度，其密度大小分布也不相同，呈现出自西向东逐渐增加的特点。

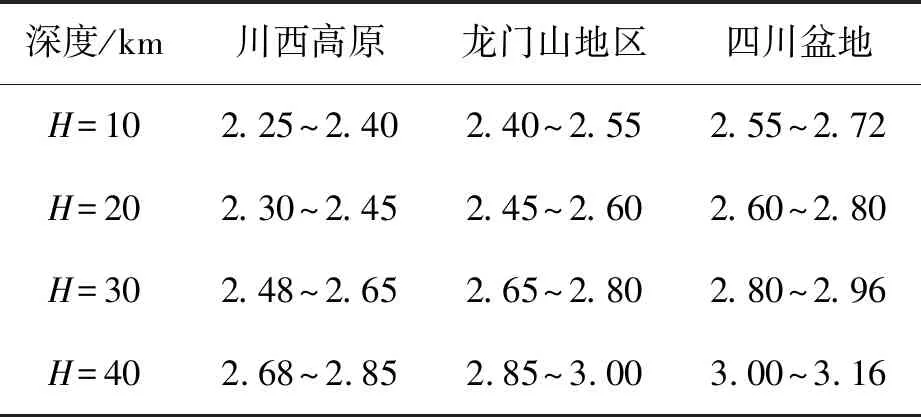
表4 密度随深度变化关系对比表

5 结论

利用GFZ提供的EIGEN-6C2超高阶卫星重力场模型，计算得到龙门山地区的自由空间重力异常，并结合界面反演确立龙门山地区莫霍面引起的区域异常，进而获取该区域的剩余重力异常，然后对该异常采用粒子群算法进行反演，最终得到该区域的三维地壳密度分布。通过分析模型反演的结果可知，龙门山地区位于密度变化的梯度带，东西两侧密度差值较大，属于密度变化强烈的区域，地下不同深度层的密度均具有西北区域低，东南区域高，以及呈现介质密度由西向东逐渐增加的特点。经过将本文所得结果与Crust1.0模型提供的密度值进行对比分析，结果表明本文所得密度分布与Crust1.0模型值的一致性较好,因此利用卫星重力数据使用Parker-Oldenburg 模型结合粒子群算法,反演三维地壳密度分布具有快速、有效和方法相对简单的特点，对于深入研究地壳介质密度有一定的参考价值。

致谢：

感谢编辑部的大力支持和匿名审稿专家的宝贵建议。