有限元重力任意复杂地形校正方法研究

朱自强，邢泽峰，鲁光银

(中南大学 地球科学与信息物理学院，长沙 410083)

0 引言

我国为多山地区，地形起伏较大，而不同地形条件对重力勘察工作有很大的影响。此外，地形校正的精度对后续重力资料的进一步处理解释影响显著[1-2]。目前，国内、外学者针对重力地形校正这一课题已进行了很多相关的研究工作，其中广泛应用于生产实践的地形校正方法包括圆域地形校正法、方形域地形校正法以及表面积分法地形校正[3-5]，其中表面积分法由于其对地形近似程度高，往往可以取得令人满意的校正精度。Bychkov等[6]利用线性解析近似的方法来进行地形校正，获得较好的地形校正结果；张伟等[7]提出基于三角网扣合的山区重力测量高精度近区地改算法，其计算精度可达“微伽级”；Cella[8]基于MATLAB开发地形校正处理程序，可较精确地实现地形校正，且可用于陆地海面等不同勘探环境。目前，我国的勘探环境越来越复杂，重力资料处理中，在地下地质体密度变化较大且地下异常体引起的重力异常信号较微弱的情况下，如果校正项出现问题，将直接影响后期数据处理与解释工作[9-10]。因此，开展任意复杂重力地形校正方法研究具有重要意义。

有限单元法因能够准确模拟复杂情况下地球物理场的分布[11]，被广泛应用于地球物理数值模拟研究工作。徐世浙等[12]通过有限单元法来求解重力场，其结果具有较高的精度和计算速率。笔者尝试采用有限单元法来研究任意复杂地形条件下有限元重力地形校正问题。采用有限单元法进行正演模拟时，不可避免的会遇到由于计算区域外地形体缺失而导致的重力异常问题。为此，这里提出一种重力补偿方法，以解决由于计算区域外地形体缺失而导致的重力虚假异常。基于改进的有限元地形体正演模拟算法，对任意地形体进行重力正演模拟，从而获得任意地形影响下在地表所引起的重力异常响应曲线，在此基础上开展地形校正，以获取任意复杂地形条件下有限元重力地形校正结果。

1 改进的有限元正演计算方法

1.1 边值问题

采用有限元法计算重力异常时，通常将边界选在远离目标体的地方，如果区域的边界取的足够远，场源对边界的影响可以近似看作质量集中于截面质心处质线的影响[12]。求解区域内的重力g就等同于求解下列边值问题[11]：

(1)

其中:G是万有引力常数；σ是密度差；θ为r与水平线的夹角；α是边界外法线n与矢径r的夹角。

1.2 变分问题

与边值问题式(1)等价的变分问题[11]如式(2)所示。

δF(g)=0

(2)

其中：Ω为计算区域；Γ∞为无穷远边界。

1.3 单元分析

对待求解区域Ω进行三角单元剖分，在三角元中进行线性插值。通过网格剖分，把积分区域剖分为许多三角形单元，从而可以把式(2)中的积分分解为各三角单元e上的积分。计算单元e的积分得

(3)

假设三角元e内的密度ρ均匀，则有

(4)

如果三角形的某一条边L落在Γ∞上，则

(5)

1.4 整体合成

在每个三角元内，将式(3)、式(4)和式(5)相加，再扩展由全体节点组成的矩阵或阵列，进而全部单元相加得式(6)。

图1 改进的重力有限元正演算法流程

(6)

其中，g是全部节点组成的列向量。对式(6)求变分，并令其等于0，得线性方程组:

Kg=P

(7)

解线性方程组，即可得到各节点的重力异常g。

1.5 改进的有限元地形体算法

基于上述有限元法对二度地形体模型进行正演模拟，由于计算范围的限制，只能考虑到预先设定计算范围内地形体在地表引起的重力响应，导致计算区域外重力响应数据缺失，从而使地形体重力响应曲线产生畸变。针对上述问题，提出一种改进的有限元地形体正演模拟算法，对缺失的重力响应做出相对应的重力补偿，以消除重力响应曲线畸变影响。改进的算法流程见图1。

2 正演算法精度验证

对地下二度密度异常球体进行有限元正演模拟，分析有限元正演模拟结果与理论重力异常间的相对误差，以验证有限元正演算法的精度。此外，利用改进的有限元地形体正演算法对水平地形体模型进行正演模拟，并将计算结果与理论曲线进行对比，分析验证该改进的有限元地形体正演算法有效性。

2.1 网格分剖

本文中的网格剖分利用了Per-Olof Persson所提供的基于MATLAB所编写的三角网格剖分开源代码DISTMESH，可通过调整网格剖分函数各项参数来达到控制每个三角网格剖分范围，网格密度以及三角网格形状等网格参数的目的。因此，可基于MATLAB利用DISTMESH开源代码进行相关模型构建，设置任意几何形状的地下异常体模型，并可实现每个网格参数独立赋值。

图2 模型1网格剖分图

图3 二度球体有限元正演模拟结果与理论曲线间拟合情况

图4 正演模拟结果与理论曲线间相对误差曲线

图5 模型2网格剖分图

图6 水平地形体不同正演模拟方法效果对比

2.2 有限元正演算法精度验证

设计模型1(图2)，假设地下密度异常体为二度球体，对该二度球体进行正演模拟，将正演模拟结果与理论曲线对比进行误差分析。模型1参数设置为，二度球体中心坐标(0，-50)，半径为25 m。假设该异常体密度均匀为2 g/cm3，背景物质密度设置为0 g/cm3，模型网格剖分如图2所示。

对模型1正演计算结果与其理论值进行对比分析，从图3中可看出，正演模拟结果和理论曲线形态相似度很高，拟合情况较好，其相对误差最大值小于3×10-4(图4)，推测其误差主要为三角形模拟近似二度球体所引起的。总体来看，该有限元正演模拟程序稳定性好，精度较高。

2.3 水平地形体模型验证

设计模型2(图5)，假设水平地形体沿水平面无限延伸，地形体垂向厚度为100 m，密度均匀且密度为1 g/cm3。模型2网格剖分如图5所示。

对模型2正演计算结果与其理论值进行对比分析，从图6中可看出，未经过重力补偿的有限元地形体重力响应曲线与理论重力响应曲线间存在明显的误差，且在地形体两端误差最大；而经过重力补偿后的有限元地形体正演模拟结果与理论重力响应曲线拟合情况较好，误差较小，证明了该改进的重力有限元地形体正演模拟算法的有效性。

3 改进的有限元任意复杂地形校正

利用上述改进的有限元地形体正演模拟算法，计算任意地形影响下地下密度异常体在地表所引起的重力异常响应，并进行有限元地形校正。

3.1 有限元任意简单地形校正

图7 模型3网格剖分图

图8 任意简单地形影响下多个密度异常体有限元正演模拟结果

设计模型3，假设地下存在多个密度异常体，任意地形体沿水平面无限延伸，从负无穷到-200，及200到正无穷范围内，地形体垂向厚度相同，设置为100 m。在-200至200范围内设置为任意起伏地形，该地形体密度均匀且密度为2 g/cm3，模型3参数设置：二度球体中心坐标(-10，-30)，半径为20 m；二度长方体左下角坐标(-115，-30)，右上角坐标为(-85,0)。二度长方体和二度球体密度均匀，与地形体相比其剩余密度分别设置为mg/cm3、ng/cm3(m,n为剩余密度的大小)。模型3网格剖分如图7所示：

利用改进的有限元地形体正演算法对上述任意简单地形体模型进行正演模拟，分析其在地表所引起的重力响应曲线分布规律。图8中，设置m=0，n=0，任意简单地形体密度均匀且密度为2 g/cm3，此时地表所引起的重力响应曲线随着地形起伏产生相对应的波动，且与地形体起伏趋势一致。地下存在密度异常体时，在异常体上方地表投影点附近重力响应曲线出现相对应向上或向下异常突出，与地形体产生的重力响应曲线混合，使地表所观测到的重力异常曲线变得极为复杂，增加后期解释工作的难度。

根据任意简单地形影响下地下多个密度异常体正演模拟结果，进一步进行有限元地形校正，得到图9中重力响应曲线。基于有限元重力地形校正结果，再进行中间层校正，得到图10中地形及中间层校正后的重力响应曲线。从图10可明显看出，不同剩余密度重力响应曲线的极值点分布在x=-100及x=-10附近，与所设置模型参数相符，重力响应曲线可更加直观可靠地反映地下密度异常体的分布情况。

图9 有限元地形校正后重力异常响应曲线

图10 有限元中间层校正后重力异常响应曲线

图11 模型4网格剖分图

3.2 有限元任意复杂地形校正

设计模型4，任意复杂地形体沿水平面无限延伸，从负无穷到-200，以及200到正无穷范围内，地形体垂向厚度相同，设置为100 m。在-200至200范围内设置为任意复杂起伏地形。地形体呈层状分布。各层密度不同；单一层内物质分布均匀，密度相同。模型4参数设置：地形体上层密度为2 g/cm3，下层密度设置为3 g/cm3；二度球体中心坐标(-10，-30)，半径为20 m；二度长方体左下角坐标(-115，-30)，右上角坐标为(-85,0)。二度长方体和二度球体密度均匀，与上层地形体相比其剩余密度分别设置为mg/cm3、ng/cm3(m,n为剩余密度的大小)。模型4网格剖分如图11所示。

图12 任意复杂地形影响下多个密度异常体有限元正演模拟结果

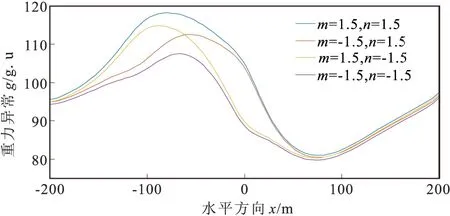
图13 有限元任意复杂地形校正后重力异常响应曲线

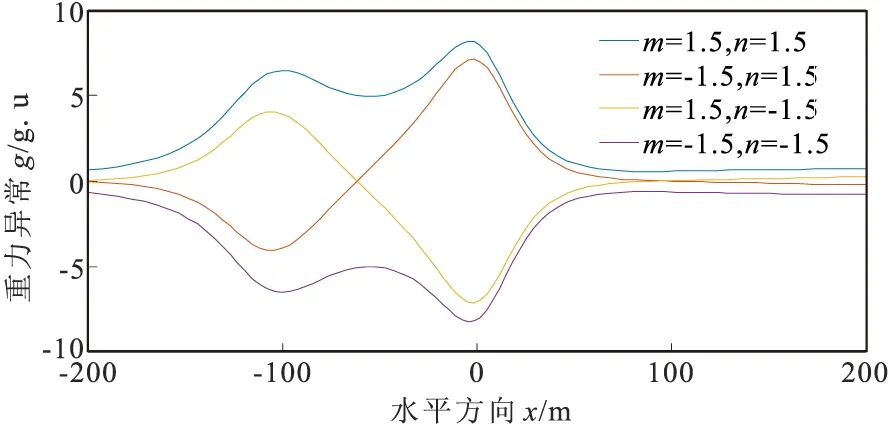
图14 有限元任意复杂地形中间层校正后重力异常响应曲线

利用改进的有限元地形体正演算法对上述任意复杂地形体模型进行正演模拟，得到地下多个异常体在地表所引起的重力响应曲线(图12)，当m=n=0时，地下无密度异常体。当地下存在多个密度异常体时，复杂地形体与多个地下密度异常体相互影响，很大程度上增大了地表所观测到重力响应曲线复杂性。

根据任意复杂地形影响下地下多个密度异常体正演结果，进行有限元地形校正。从图14可看出，任意复杂地形影响下经有限元地形校正及中间层校正后重力响应曲线可更加直观地反映地下密度异常体分布状态，可明显区分两个异常体的位置分布，验证了该有限元地形校正算法的有效性。

4 结论

利用笔者提出改进的重力有限元任意地形模拟算法对任意地形影响下地下多个密度异常体进行正演模拟，获得地表处的重力响应曲线，经校正后的重力响应曲线更加直观地反映出地下密度异常体分布状态，验证了该有限元任意复杂地形校正算法的有效性。

基于有限元法可建立任意形状、任意密度复杂地下模型。在保证计算精度的情况下，可快速计算出重力任意复杂地形校正结果，有限元重力任意复杂地形校正方法尤其适合于地下地质体密度变化较大的复杂地形。