基于机器学习理论的海洋水质评价模型

张 莹，谢仕义，邓伟彬，彭发定，余昱昕, 张培珍

(广东海洋大学 a.数学与计算机学院;b.电子与信息工程学院，湛江 524088)

0 引言

随着我国经济社会的迅速发展和城市化进程的不断加快，水资源短缺、水体污染严重已成为制约经济社会可持续发展和人民生活水平提高的重要因素。《2017年中国海洋生态环境状况公报》显示，我国海洋生态环境状况不容乐观，近岸局部海域污染依然严重。全国417个监测点位中，一类海水比例为34.5%；二类为33.3%；三类为10.1%；四类为6.5%；劣四类为15.6%，加强对所属海域的环境监测和保护工作迫在眉睫。

海洋水质评价的内容就是根据海水水体的主要物质成分及其含量，分析各类水质的时空分布状况[1-2]。已有的评价方法主要有单因子指数法[3-4]、综合指数法[4-6]、分级评价法[7-9]等，以及模糊理论、灰色系统理论、投影寻踪及神经网络等方法[9-11]。相比这些传统的统计学、模式识别领域的算法，大数据下的机器学习大大扩充了样本的数量，使很多问题的分类都有丰富的样本作为支撑[12]，能够有效解决这种多维因子组成系统的评价问题。因此，本研究拟利用数据量丰富的样本，选择适当的用于多特征多分类问题的机器学习算法，构建适用于海水水质的综合评价理论模型。

1 水质评价的样本

按照GB3097-1997《国家海水水质标准》[13](表1)，建立40×104个站位组成，每个站位包含13个水质指标信息的理论假设样本。

2 机器学习

2.1 算法原理2.1.1 决策树

决策树是最简单的机器学习算法,它易于实现，高度可解释，完全符合人类的直觉思维。简单地说，决策树是二叉或多叉树，它判断数据的属性并获得分类或回归结果[14]。决策树是支持多类分类问题的判别模型。在预测中，某个属性值(特征向量的某个组成部分)用于树的内部节点，根据判断结果确定要进入哪个分支节点，直到到达叶子节点，并获得分类或回归结果。决策树的这些规则是通过机器训练而不是人为获得的。

表1 国家海水水质标准

在训练时，我们需要找到一个拆分规则，将训练样本集分成两个子集。通过一种衡量标准，来计算通过不同特征进行分支选择后的分类情况，找出来最好的那个当成根节点，以此类推。对于分类问题，确保左右子树的样本在分裂后尽可能纯，即它们的样本尽可能接近某个类。为此，定义一个不纯的指标：当样本属于某一类时，不纯度为0；当样品均匀的属于不同类时，Gini不纯度最大。

使用样本集中每种类型样本的概率值构建杂质指标。因此，首先计算每个类的出现概率，设训练样本集中总样本数为N，其中第i类样本数为Ni，则每个类的出现概率可表示为式(1)。

pi=Ni/Ni=1,2,…,n

(1)

样本集的熵不纯度[15]可表示为式(2)。

(2)

熵是表示随机变量不确定性的度量。当样本仅属于一个类时，熵是最小的，当样本在所有类中均匀分布时，熵是最大的。所以找到一个分裂让熵最小，即为最佳分裂。

样本集的Gini不纯度[15]可表示为式(3)。

i=1,2,…,n

(3)

当样本属于某一类时，Gini不纯度的值最小，最小值为0；当样品均匀分布时Gini不纯度值最大。

样本集的不纯度[15]可表示为式4)。

E(D)=1-max(pi)i=1,2,…,n

(4)

以上定义的是样本集的混乱程度。需要评估的是分裂的质量，分割规则将节点的训练样本集分成两个左右子集。分裂目标是将数据分成两部分，两个子集尽可能纯。因此，计算左右子集的不纯度之和为分裂的不纯度。实际上，求和需要加权以反映两侧的训练样本的数量。

设G(DL)是左子集的不纯度NR，NL是左子集的样本数，G(Dn)是右子集的不纯度，NR是右子集的样本数，N是样本总数，得到的分裂不纯度计算公式为[16]式5)。

(5)

如果采用Gini不纯度作为划分标准，代入式(5)得式(6)。

i=1,2,…,n

(6)

式(6)值越小，样本越纯。要查找最佳分割，需要在将样本集拆分后计算此值，并在值为最小值时找到相应的分割，这是最好的分裂。

2.1.2 贝叶斯

贝叶斯分类器是可以处理多分类问题的生成模型，并且是非线性模型。朴素贝叶斯分类器基于贝叶斯分类方法，数学基础是贝叶斯定理，它描述了统计条件概率之间的关系。贝叶斯分类器的核心就是将样本判定为后验概率最大的类[17]。

已知样本的特征向量为x={a1,a2,…,an}，类别标签为L={y1,y2,…,yn}，根据贝叶斯公式，样本属于每个类的条件概率(后验概率)为[18]式(7)。

i=1,2,…,m

(7)

对于所有的分类标签y1、y2、…、ym，其P(x)都是相同的，在比较P(yi|x)，…，P(y4|x)的时候我们可以忽略P(x)这个参数。所以分类器的判别函数为式(8)。

argmaxyP(x|yi)P(yi)

(8)

对于给定的观测数据，一个猜测是好是坏 ，取决于“这个猜测本身独立的可能性大小即先验概率”和“这个猜测生成我们观测到的数据的可能性大小”。

假设样本服从高斯分布，在训练期间确定先验概率分布的参数，通常使用最大似然估计，即最大化对数似然函数。

2.1.3 支持向量机

支持向量机(SVM)是非常强大和灵活的有监督学习算法，可用于分类和回归。SVM的目标是通过使用分界线(2D空间中的线或曲线)或流形体(多维空间中的曲线，曲面等)来分离各种类型的数据，得到的分类超平面不仅可以正确地对每个样本进行分类，并且还要使得每一类样本中距离超平面最近的样本到分类线的距离尽可能远，支持向量机实际上是边界最大化评估器[19]。

最大间隔和最佳超平面仅完全由落在边界上的采样点确定。这样的采样点称为支持向量[20]，其余的非支持向量采样点对确定分类超平面无效，找到最优超平面等同于确定支持向量，并且由支持向量确定的线性分类器称为线性支持向量机。

设训练样本的特征向量为xi,i=1、2、…、n，类别标签为y∈{+1,-1}，则分类超平面方程[21]可表示为：

(w·x)+b=0

(9)

其中：w为权重向量；b为偏置项，是一个标量。为了能正确分类并且有一定间隔，要求分类超平面方程满足以下约束：

yi[(w·xi)+b]≥1i=1,2,…,n

(10)

(11)

最后通过构造拉格朗日子乘函数得到最优分类函数为：

(12)

其中:sgn为符号函数;αi、b为确定最优划分超平面的参数;(xix)为两个向量的点积。

创建一个简单的支持向量机线性分类器，如图1所示。支持向量机的优化目标就是找到一条线，使得离该线最近的点能够最远，此外蓝色标记的点为拟合数据的关键支持点，称之为支持向量。分类器可以成功拟合的关键因素是这些支持向量的位置，远离边界的数据点对分类器完全没有影响。

对于线性不可分割的情况，支持向量机的主要思想是通过一个二元函数k(x,y)即核函数将特征向量映射到高维特征向量空间，并在特征空间中构造最优分类面，使得原来线性不可分的数据在映射之后变得线性可分。

使用核函数k后，非线性支持向量机分类器的最终分类决策函数为：

(13)

常用的核函数见表2。

图1 支持向量机线性分类器

表2 常用核函数

除了选择核函数外，非线性支持向量机模型还需要为参数C及gamma设置恰当的值。参数C越大则精度越高，反之则分类边界线容错率更高，泛化能力很强。参数gamma是多项式核、径向基函数核及sigmoid核的参数。参数对分类器的性能至关重要，为SVM获取最优的参数使非线性支持向量机模型能对数据有更好的拟合。

3 实际应用

3.1 计算过程

水质评价问题中，G=4，分别代表四类水质；每类水质100 000个样本，即n1=n2=n3=n4=100 000,N=400 000,m=13。

3.1.1 数据读取

将13个海水水质评价指标作为样本特征x，将四种水质类别作为分类标签y，最终机器学习是通过样本特征x得出具体水质分类y。

3.1.2 数据切分

先把数据集x、y按相同的随机方式进行洗牌，然后把数据集切分成训练集和测试集。训练集占80%共32×104个数据，设x_train为训练集的特征属性，y_train为训练集的分类标签；测试集占20%共8×104个数据，设x_test为测试集的特征属性，y_test为测试集的分类标签。

3.1.3 数据标准化

由于水质指标的量纲不相等，因此必须对数据进行标准化以消除量纲影响, 将原始数据集x_train和x_test归一化为均值为0、方差1的数据集，使得在最开始的时候，各个特征之间的重要程度的是一样。标准化公式为式(14)。

(14)

其中:μ、σ分别为原始数据集的均值和方差。

3.1.4 机器学习模型

1)决策树：通过预剪枝策略指定决策树模型的最大叶子节点为13，以此避免决策树过拟合，切分标准为熵不纯度。构建好模型就可以对x_train、y_train训练集数据进行训练。决策树的每一个节点中都有分类特征的判断，熵不纯度entropy，样本数量samples及分类的数据values。其中熵值为2.0，样本数量为320 000，数据分为4类，对应4类水质。可以得到决策树每一次进行分裂后熵值必定会较上一层小，数据变得更纯净。

2)贝叶斯：构建高斯朴素贝叶斯分类器。利用x_train、y_train训练集32×104个数据对高斯朴素贝叶斯分类器模型进行训练。查看高斯朴素分类器的P(yn)有：P(y1)=0.24982813,P(y2)=0.24962813,P(y3)=0.25004668,P(y4)=0.25049688。

3)支持向量机：此次数据分类为多特征多分类问题，而标准的支持向量机只支持二分类问题，因此，构建使用径向基函数核的非线性支持向量机模型来解决数据线性不可分问题。选择最佳参数时，需要确定的参数有惩罚参数C及函数核参数gamma。先设置好参数列表，通过网格搜索找出最佳参数，如果最佳参数落在网格边缘则继续调整参数列表，直至最佳参数落在网格中间，使用最佳参数能使非线性支持向量机模型能对数据有更好的拟合。通过网格搜索得出的最佳参数为：C∶107 000,gamma∶0.001为SVM获取最优的参数，使非线性支持向量机模型能对数据有更好地拟合。

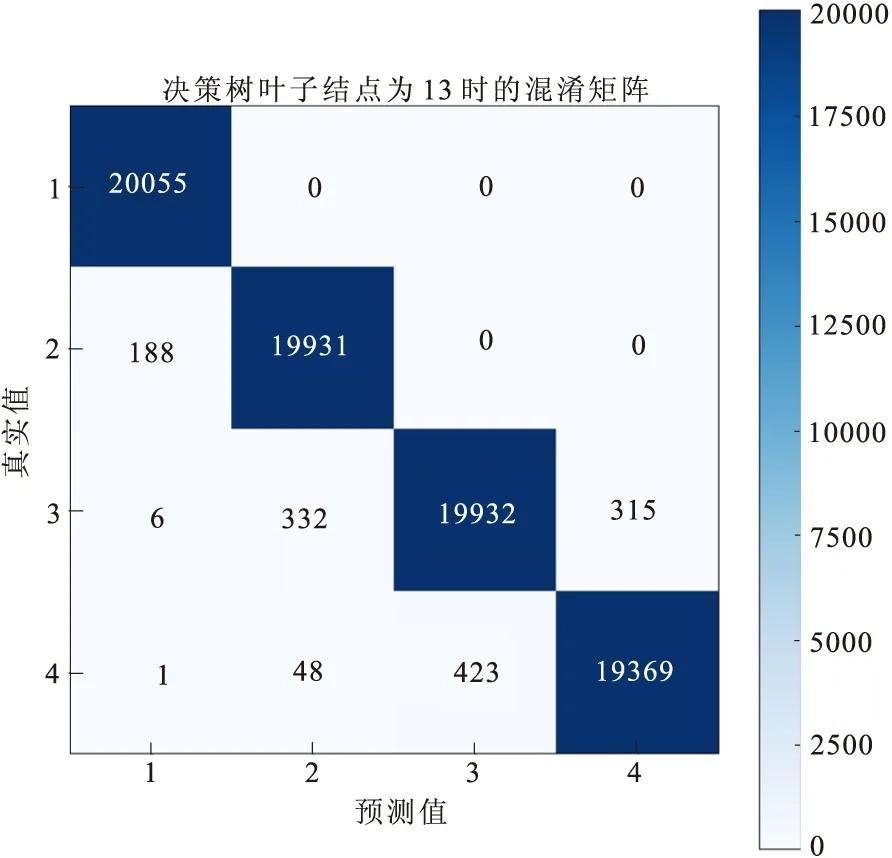
图2 决策树模型的混淆矩阵

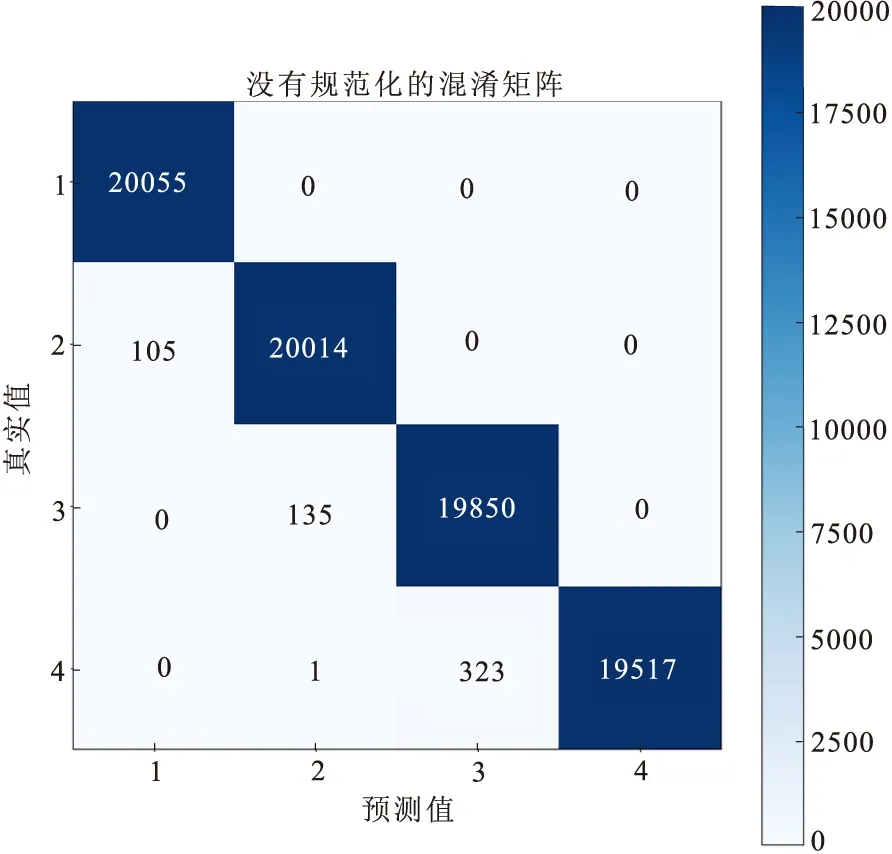
图3 高斯朴素贝叶斯模型的混淆矩阵

图4 非线性支持向量机模型的混淆矩阵

3.1.5 评估模型准确性

分别利用已训练好的决策树模型，高斯朴素贝叶斯模型和非线性支持向量机模型对测试数据集的x_test进行分类预测得出分类结果y_pred。然后用x_test及y_test测试数据集对该模型进行精度评估，得出决策树模型的精度为98.358 75%，高斯朴素贝叶斯模型的精度为99.295%，非线性支持向量机模型的精度为99.542 5%。

利用y_test和y_pred画出混淆矩阵，图2为决策树模型混淆矩阵，图3为高斯朴素贝叶斯模型混淆矩阵，图4为非线性支持向量机模型混淆矩阵，X轴为预测值的水质分类，Y轴为真实值的水质分类。可以看出决策树模型容易把第三类水质分类成第二类和第四类。第四类水质也较容易分类成第三类水质。高斯朴素贝叶斯分类模型第四类水质较容易分类成第三类水质。非线性支持向量机模型效果最佳。

4 结论

1)本研究基于大数据与机器学习理论，按照GB3097-1997《海水水质标准》建立了一个由400 000站位水质信息组成的理论假设大样本，通过三种适用于多特征多分类问题的机器学习算法的应用，构建了适用于海水水质的综合评价理论模型。

2)适用于海洋水质评价问题的决策树算法，是通过预剪枝策略指定了决策树模型的最大叶子节点数量，其切分标准为熵不纯度。适用于海洋水质评价问题的贝叶斯算法，选用了高斯朴素贝叶斯分类器模型。适用于海洋水质评价问题的支持向量机算法，是使用径向基函数核的非线性支持向量机模型。

3)通过8万个站位测试样本的验证，决策树模型的精度为98.358 75%，贝叶斯模型的精度为99.295%，支持向量机模型的精度为99.542 5%，均可作海洋水质评价问题的有效方法，其中的支持向量机模型效果最好。