基于Hankel矩阵的随机噪音衰减法在煤田勘探中的应用

蔡文芮

(中煤科工集团 西安研究院有限公司，西安 710077)

0 引言

随着煤炭开采机械化程度的不断提高，对小构造地震勘探精度的要求也越来越高。为解释人员提供更真实可靠的地震数据体，是地震数据处理人员所要面对的问题。在“高信噪比、高分辨率、高保真度”的要求中，信噪比是基础，高保真度是目标，而如何在提高信噪比的同时又要不伤害有效信号，是地震资料处理的难点问题。

在煤田地震资料处理领域，叠后随机噪音衰减一直是地震数据处理的一项重要手段，因为叠后随机噪声的存在会大大降低地震资料的信噪比，影响最终的剖面质量，也制约着后续的构造解释、属性反演精度。Canales[1]提出采用f-x域预测去噪技术压制二维地震剖面的随机噪音;国九英等[2]在此基础发展出f-xy域预测技术进行三维随机噪音衰减，该方法充分利用了三维空间信息，与f-x域预测方法相比，去噪能力更强，波形更自然;李淅龙[3]、邹梦等[4]采用三维正交多项式拟合技术进行叠后随机噪音衰减，通过构建多项式来拟合地震信号，恢复反射同向轴的连续性，达到了增强有效信号提高信噪比的目的。这些方法能够较好地衰减随机噪音，提高剖面的信噪比，在煤田地震勘探实际资料处理中得到了广泛应用。上述叠后去噪方法，都是假定噪声是白噪的、有效波是连续的、可预测的，从而采用预测法或拟合法去逼近有效波，并没有真正地分离有效信号和噪音。在实际地震资料处理中，这些假设条件很难完全满足，因此去噪后剖面会出现蚯蚓化现象，导致小断层变得模糊不清，不符合小断层高精度地震探测的要求。如何在去除噪音、提高信噪比的同时，又能够最大程度地保护有效波，尤其是小断层、陷落柱等，是当前煤田地震数据处理面临的难点之一。

近年来，随着现代信号技术的不断发展，基于现代信号分析的地震数据去噪方法也得到了不断地发展，如小波分解与重构、奇异值分解滤波、矢量分解方法、基于匹配追踪算法的时频滤波方法、径向道变换方法等。其中奇异值分解滤波法是一种对地震数据进行奇异值分解，通过选取前N个特征谱进行信号重建从而达到提高剖面信噪比的目的方法。该方法利用了地震信号在时间域的相关性，因此对水平同相轴的去噪效果明显，且保真性较高，但对于倾斜、弯曲的同相轴的去噪效果不好。针对这个问题，Cadzow[5-7]提出将地震信号由时间域变换到频率域，对每一个频率切片构建Hankel矩阵，通过奇异值分解，选取前N个奇异值对应的本征图像来重构地震信号，从而达到提高剖面信噪比的目的。崔少华[8-9]、彭更新等[10]对该方法进行了二维地震数据模型测试，并将此算法与传统奇异值分解滤波算法进行比较；崔树果[11]、鲁玲[12]提出了块Hankel矩阵大大降低了奇异值分解的工作量，提高了运算效率；张唤兰[13]将该方法用于微地震数据处理中，取得了较好的效果。

1 基于hankel矩阵变换的滤波原理

Hankel 矩阵就是反对角线上的元素相等的一种特殊矩阵，被广泛应用于信号处理、数值计算、系统分析等领域[14-17]。

假设一个时间域的地震信号可以表述为，通过傅里叶变换将该信号转换到频率域，在它的频率f处抽取该数据的频率切片，该频率对应的函数值可以表述为s=s(f)=[s1,s2,s3,…,sn]T。利用s(f)构建一个hankel矩阵H

(1)

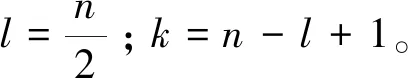
假设一个含有m个倾角的地震剖面，由于信号在频率-空间域具有可预测性，所以某一频率f的信号可以表达为：

(2)

其中:Pd(d=1，2，…，m)为预测滤波器；n为地震信号的道数。公式(2)表明，Sj可以由前面j-d个点预测出来，由Sj构造的Hankel矩阵经过运算后有效秩不超过倾角的个数m，当N等于m时信号就可以被完整的恢复出来。

对矩阵S进行奇异值分解，得到：

(3)

其中:U和V分别为左、右奇异值矢量，U为一个n*m阶的正交矩阵；ui矩阵SST是第i个特征向量。V为一个m*m阶的正交矩阵；vi为矩阵STS第i个特征向量；E为SST的奇异值按递减顺序组成的对交矩阵，E=diag{σ1、σ2、…、σk,0、…、0}。该矩阵的秩k=rank(S)=min(m,n),奇异值分解即可以看成将矩阵S分解为k个本征图像的的加权和，可以表示为：

S=S1+S2+S3……+Sk

(4)

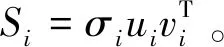
矩阵S的总能量可以表示为：

(5)

由公式(5)可以看出，矩阵S经过奇异值分解后，总能量可以用奇异值平方和来表示。当对地震数据进行奇异值分解时，由于有效信号是相干的、有规律的，所对应的奇异值越大。而随机噪音是一种没有规则，杂乱无章的，对应的奇异值越小。因此，选取N个较大的奇异值来重构地震数据，即可达到去除随机噪音的目的。

2 实现方法

假设S是一个采样点为m，总道数为n的二维地震记录，对该二维地震数据进行基于Hankel矩阵的随机噪音衰减，可以由以下六个步骤完成：

1)将该二维地震记录以道号为顺序，沿每一道的时间轴对该地震记录进行傅立叶变换，得到了频率域的数据体F_X。

2)提取频率域数据体F_X的第一个频率切片数据F1。按公式(1)将提提取的频率切片数据构建Hankel矩阵。

(6)

3)按公式(3)对构建好的Hankel矩阵进行奇异值分解,得到按大小顺序排列奇异值σ1>σ2>…σk>0。

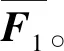
5)依次对每一个频率切片重复步骤3)、步骤4)，直至频率域数据体中所有的频率切片都被重构。

6)对处理过的频率体数据进行反傅立叶变换，将地震数据由频率域回到时间域，最终得到重构去噪后的时域地震记录。

对三维地震数据进行处理时，依次抽取每条线，即可按照二维方法进行去噪。

3 实际地震资料处理及效果分析

选取永城煤田某矿三维地震资料，该区是一典型的复式背向斜构造，新生界覆盖于含煤地层之上。受多期构造运动影响，断裂发育(图1)。该区地震地质条件较好，具有统一的潜水位，激发条件好，但由于上覆新生界地层较厚(约400 m)，加之上组厚煤层的屏蔽作用，致使深部煤层反射波能量较弱。从初叠剖面(图1)可以看出，上覆第四系、石炭系和二叠系含煤地层均能形成较好的反射波。由于构造复杂，小断层密集发育，对地震资料的解释要求很高，除要解释3 m以上断层外，还需对3 m以下小断层(点)进行构造解释。因此，对地震处理数据的要求是高保真和高分辨率，先要保证处理结果的真实性，再提高资料的信噪比和分辨率。

3.1 数据预处理

为了保证小断点的可靠性，在数据处理阶段，均采用保真性较高的处理流程。在振幅恢复方面，采用球面扩散补偿及地表一致性振幅补偿来恢复地震波的振幅相对关系，避免使用损伤振幅关系的增益均衡模块。针对该区面波发育的特点，采用保真性较高的十字交叉域面波衰减法。在偏移成像方面，通过多次优化迭代建立高精度的速度场，并通过反复参数试验，选取最佳偏移孔径、偏移角度及去假频等参数进行叠前时间偏移处理,使能量较好的归位，得到了质量较高的叠前偏移剖面。

3.2 参数选择

该方法利用对地震数据构建的Hankel矩阵进行奇异值分解后，数值大的奇异值对应相关性较强的有效信号，数值小的奇异值对应相关性较弱的随机噪音，通过选取代表有效信号的前N个奇异值重构数据从而达到去除随机干扰的目的。较大的N值能够保证有效信号被完整的重构，但会造成噪音残留，影响随机噪音衰减的效果。N值过小，又会损伤有效信号。因此，N值的选择成为Hankel矩阵去噪方法中最关键的参数，只有选择合适的N值才能在高效压制随机干扰的同时不损伤有效波。

从公式2)可以看出，选取与同相轴倾角个数相同的前N个奇异值进行信号重构时，就可以达到去除随机噪声重建地震有效信号的目的。在沉积环境稳定，构造简单的地区，可以直接根据地层倾角选取与倾角个数相等的N值。但在沉积环境复杂，受多期构造运动影响，构造复杂、小断层较多的区域，无法精确确定地层倾角个数，就需要在估算地层倾角的基础上，进行N值的测试，通过实验选择最佳的N值。

3.3 效果对比

从处理结果来看，叠前偏移剖面已经能够较为清晰地反映该区的地质构造。由于随机噪音干扰的存在，剖面显得信噪比较低，小断点模糊不清，因此采用基于Hankel的方法对该剖面进行随机噪音衰减提高剖面信噪比。由于该区地质构造复杂，地层倾角变化大，无法精确确定地层倾角个数，综合全区地层倾角变化情况，分别选取N=2、3、4、5进行参数测试。试验结果表明，当N=3时去噪效果好，且能最大程度地保护有效波。

与此同时，采用煤田生产常用的多项式拟合法进行效果对比。图1(a)是该区经过保幅处理的叠前时间偏移剖面；图1(b)是经过多项式拟合去噪剖面；图1(c)为基于Hankel矩阵的随机噪音衰减法去噪后的剖面。可以看出，经过多项式拟合去噪后，图1(b)剖面信噪比得到了较大地提高，但圈中同相轴的轻微错断以及振幅异常突变被模糊掉了。图1(c)显示，经过基于Hankel矩阵的随机噪音衰减法去噪后，剖面信噪比提高的同时，保留了同相轴轻微错断和振幅异常突变。对两种去噪方法所去除噪音剖面进行对比，图2(a)多项式拟合去噪后的噪音剖面，除了随机噪音外还有大量的有效反射波残留，且能量较强，说明该方法虽然能较好地提高信噪比，但同时也会损伤有效信号；图2(b)是Hankel矩阵去噪后的噪音剖面，以随机噪音为主，并没有发现有效波残留，说明该方法能够分离噪音与有效波，在去除噪音的同时不伤害有效波，具有较好的保真性。图3为Hankel矩阵去噪前后振幅信噪比的对比，可以看出：经过Hankel矩阵去噪后，噪音绝对振幅值由近90 000降到60 000，而有效信号的绝对振幅值在去噪前后并没有较大的变化，说明该方法能够较好的保持振幅，具有较好的保幅性。

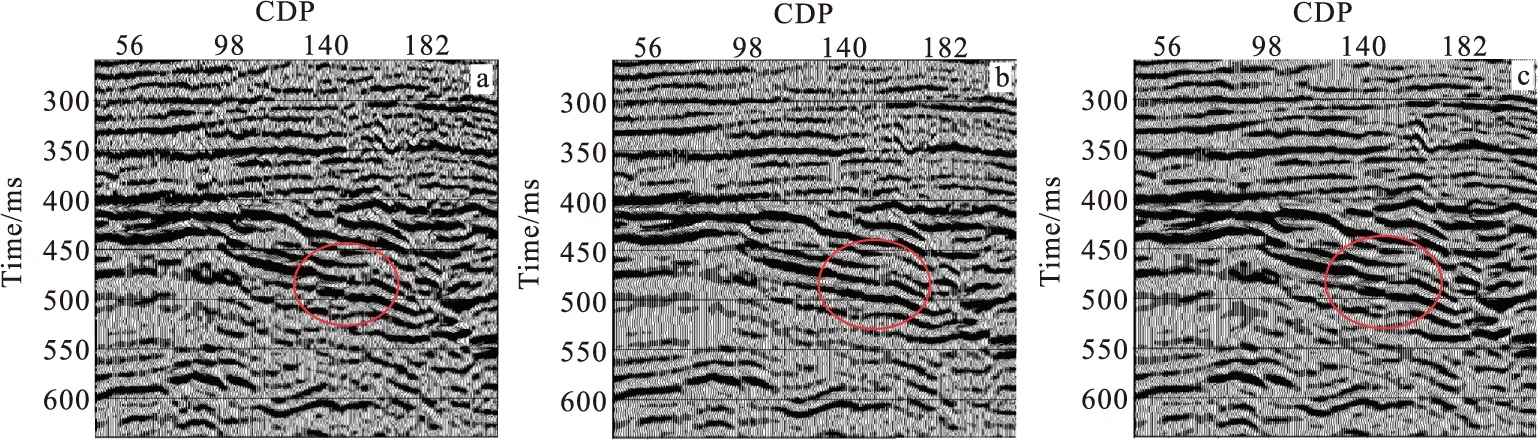
图1 不同方法去噪前后剖面对比图

图2 不同方法去噪后噪音剖面对比图

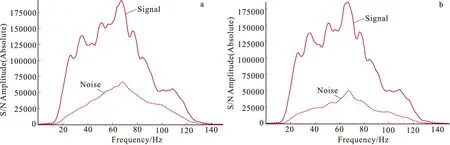
图3 不同方法去噪前后信号与噪音振幅对比图

4 结论

1)基于Hankel矩阵的随机噪音衰减法从原理上解决了非水平同相轴去噪难的问题，能够很好地去除含有倾斜地层的随机噪音。

2)利用该方法进行随机噪音衰减，去噪后波形真实自然、小断层断点清晰，且去噪后的剖面中没有相干有效信号残留，具有良好的保真性。

3)振幅能量信噪比分析表明，该方法在大幅度降低噪音能量的同时，并未损害有效信号的振幅能量水平，因此具有较好的保幅性，有利于后续的属性分析和岩性反演。

4)该方法是对地震数据逐道建立Hankel并进行奇异值分解再进行重构，计算量较大，对计算机性能要求较高。

5)与多项式拟合去噪法相比，该方法无论从去噪效果还是信号的保真性和保幅性，都有较大的优势，在煤田地震勘探领域具有较好的推广价值。