2.5维各向异性介质直流电法异常场的正演模拟
柯颂颂,宋 滔,刘 云
(1.中国科学院 地球化学研究所矿床地球化学国家重点实验室, 贵阳 550002;2.中国科学院大学,北京 100049)
0 引言
直流电阻率法各向同性的正反演技术已经比较成熟,并且在工程、找矿等领域有了广泛应用[1-2]。随着数值模拟技术的发展,研究的热点聚集到了更符合实际情况的连续介质和各向异性介质。
对连续介质的研究,徐世浙[3]使用有限单元法矩形单元剖分;阮百尧[4]使用三角单元剖分,实现了对连续介质的数值模拟,取得较高精度;刘云[5]在阮百尧的基础上,使用矩形内剖分四个三角形的剖分方式实现了对连续介质、复杂地形以及复杂模型的数值模拟。
近年来,对各向异性直流电法的研究也越来越多[6-9]。但关于直流电阻率法2.5维各向异性正演模拟的研究相对较少。徐世浙等[3]使用有限单元法对二维各向异性的直流电阻率法进行了模拟;Zhou等[9]使用高斯正交网格(Gaussian quadrature grids)实现了对2.5维复杂各向异性介质的数值模拟,取得较好的精度。由于三维各向异性参数太多,导致基于三维各向异性正演的反演研究工作进展缓慢,所以研究直流电阻率法2.5维的正反演方法成为探索各向异性反演工作的桥梁。在前人的研究中2.5维正演均是基于总场法的,因为异常场法需要求解一次场,而电性各向异性介质点源傅氏空间中的解析解较难求得,所以关于2.5维各向异性介质异常场法的研究较少。
这里给出各向异性介质2.5维总场和异常场的变分问题。在实现异常场法时,因为将点源各向异性介质空间电位转换到傅里叶空间中具有一定困难,所以笔者进行了简化处理,假设点源附近的介质为主轴各向异性,从而实现2.5维各向异性介质异常场法的模拟,通过算例证明该方法的正确性。
1 变分问题
一般定义各向异性电阻率为张量形式[11],如式(1)所示。
(1)
选取如图1所示的观测坐标系,z方向为垂直方向,x、y方向为水平方向,假设介质构造为x方向,即沿x方向介质没有变化,设介质电性主轴的平面x′y′与坐标轴xy平面的夹角为α,此时电阻率张量表达式(1)中旋转矩阵D为:
(2)
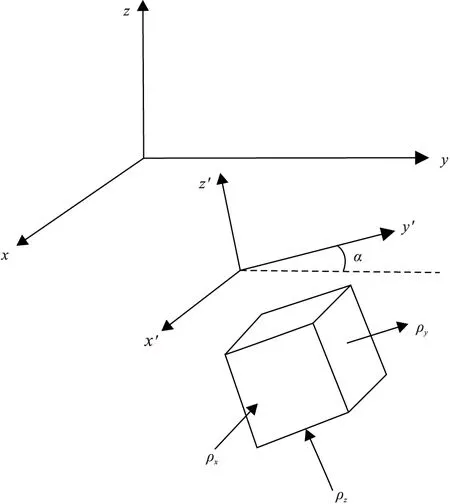
图1 二维各向异性
将式(2)代入式(1)中得到介质的电阻率张量为:
(3)
相应的电导率为:
(4)
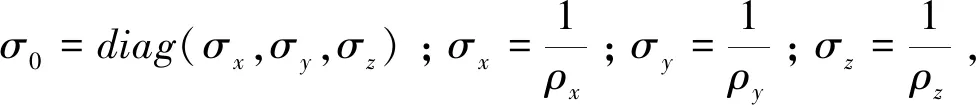
(5)
根据Zhou[9]、严波[11]等的推导,傅里叶空间中的电位U满足的边值问题如式(6)所示。
(6)
对应的变分问题如式(7)所示。
(7)
当采用异常场法模拟时,将总场分为背景场(一次场)和异常场(二次场),以消除源的影响,提高模拟精度。
与各向同性的边值问题和变分问题类似,我们给出异常场满足的变分问题如式(8)所示。
(8)
2 有限单元法
2.1 区域剖分
首先将整个区域剖分成矩形单元,然后再将每个矩形剖分成两个三角形,如图 2所示。
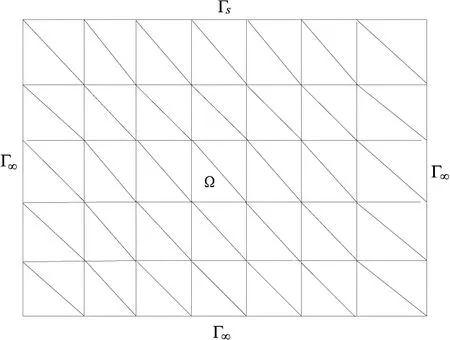
图2 区域剖分
在三角单元内假设电位是线性变化的,在单元内任意位置的电位u可以通过形函数和三角形三个节点的电位表示,如式(9)所示。
u=Niui+Njuj+Nmum=NTu=uTN
(9)
其中:NT=(Ni,Nj,Nm)为形函数;uT=(ui,uj,um)为三角形节点的电位。
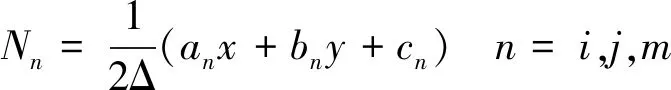
其中:Δ为三角形的面积,且有:
2.2 单元分析
将式(8)中的积分在区域离散化,表示成所有单元的线性组合如式(10)所示。
(10)
式(10)中的积分项依次记为积分1、2、3、4、5和6。
根据严波[11]等的推导,以及积分1和积分4的相似性,得到:
(11)
(12)
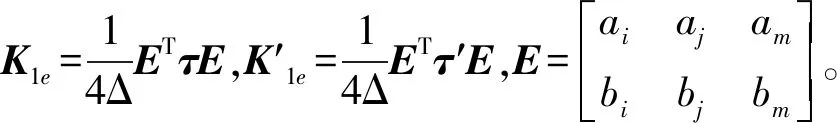
单元积分2和积分5为:
(13)
(14)
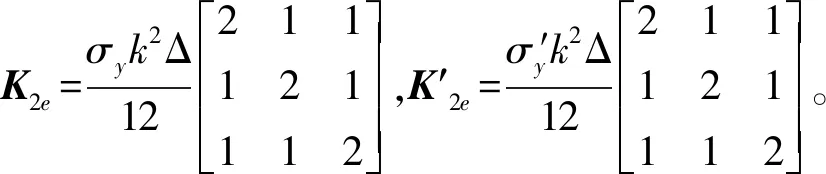
单元积分3和积分6为:
(15)
(16)
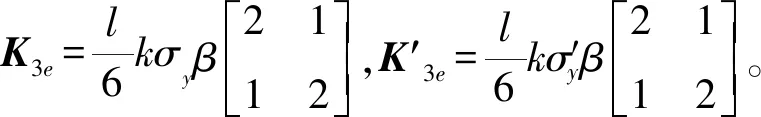
将单元矩阵添加到整体系数矩阵中的相应位置,得到式(17)。
(17)
令式(17)的变分为0,得到线性方程组(18)[3]。
(18)
解线性方程组得到波数域中异常场的电位,进行傅里叶反变换得到空间场中的异常场电位,最后加上一次场电位得到总场电位。
2.3 欧拉角的简化
观察式(17)和式(18),要得到方程组还需计算波数域中的一次场电位U0,点源均匀半空间各向异性介质电位表达式为式(19)[12]。
(19)
其中B=(r-r0)T·ρ·(r-r0),将B展开后,直接使用该表达式进行傅里叶变换较为困难,因此笔者采用简化欧拉角的方法进行处理。假设二维构造下点源附近的介质(背景介质)电性主轴与观测坐标系的夹角为零得到:
ρ=diag(ρx,ρy,ρz)
(20)
对式(20)进行傅里叶变换,得到傅氏空间中电位表达式为式(21)。
(21)
得到波数域中的一次场后,代入有限元公式进行计算,将角度信息也作为异常来处理,由有限元完成计算异常场的工作。
此处我们假设了背景电阻率的电性主轴与观测坐标系的夹角α为零,所以该方法对α≠0的模型并不适合。
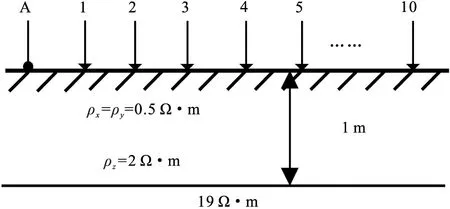
图3 模型1:两层含VTI介质模型
3 算例分析
3.1 两层含垂直各向异性(VTI)介质的地电模型
设计一个两层单界面模型,其中第一层为VTI介质,第二层为各向同性介质,模型和电极布置如图3所示。发射电极为A点,模拟供入1A的电流,1~10为接收电极且电极之间距离为1 m。
3.1.1 算法验证
分别使用总场法和异常场法进行模拟,选用的波数为徐世浙[3]计算的最优波数。异常场法中背景场设为ρx=ρy=0.5 Ω·m,ρz=2.0 Ω·m产生的电场,也即点源处的电阻率作为背景电阻率。将总场法与异常场法的数值模拟结果与解析解分别进行对比,如表1所示。
从模拟结果可以看出,使用异常场法精度较高,误差均在1%以内,而总场法在点源附近误差较大,并且整体的误差也较异常场法较高,也证明了本文算法的正确性和准确性。
3.1.2 波数的讨论
在以上计算中,如果采用宋滔等[14]计算的7点波数,总场法和异常场法的计算结果分别与解析解对比,相对误差如表2所示。
从结果中可以看出,异常场法模拟的结果误差非常小,但是总场法采用7点波数的模拟结果与解析解的相对误差较大。这是因为在波数域中点源附近有限元解误差较大,所以变换到空间域时误差也较大;7点波数本来的精度是较高的,即如果有限元解越精确,得到空间域的电位也越准确,相反如果解的误差较大,使用七点波数反而会使空间域的电位误差变大。
因为在地形条件下无法使用异常场法,所以在各向异性的正演模拟中用总场法时采用5点波数;采用异常场法时选用7点波数,可以取得相对更高的精度。
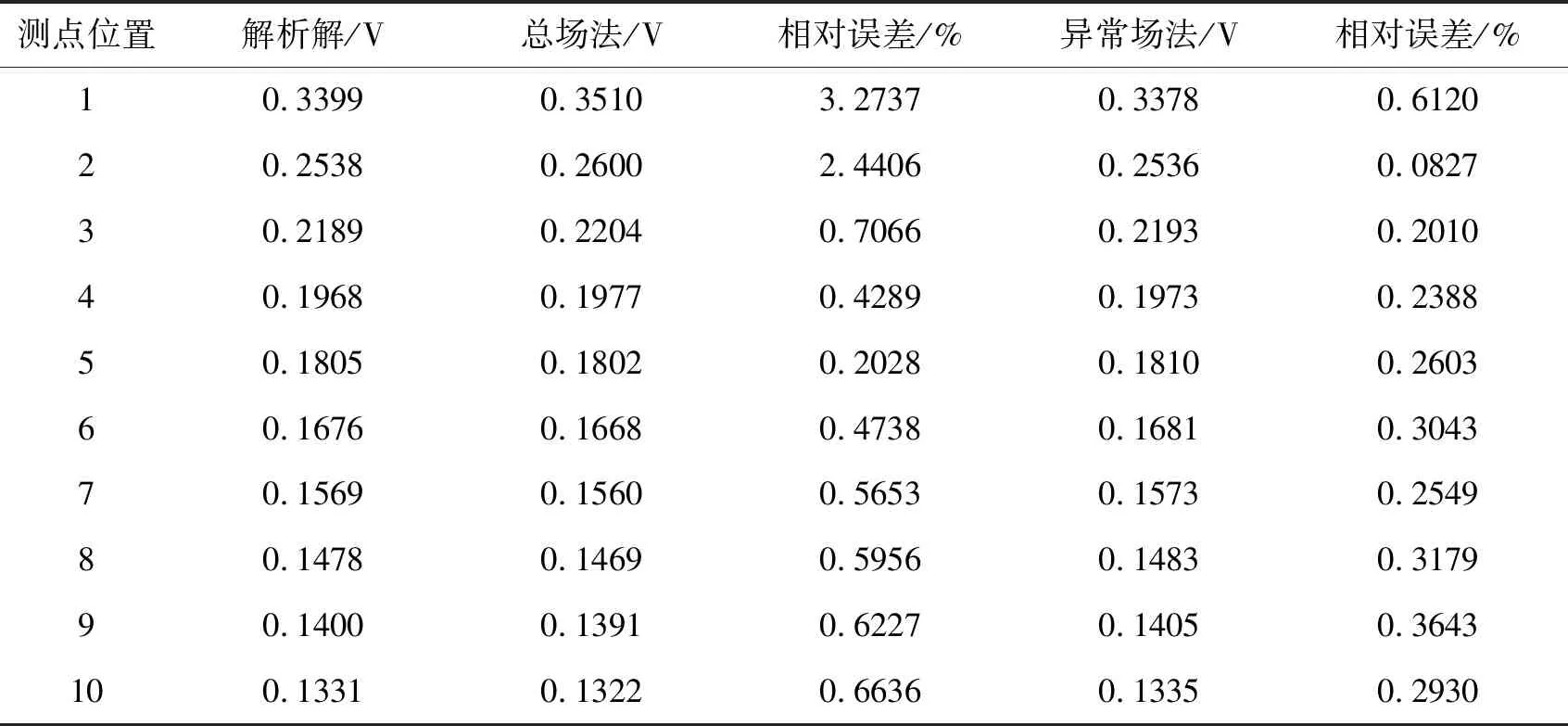
表1 数值解与解析解对比
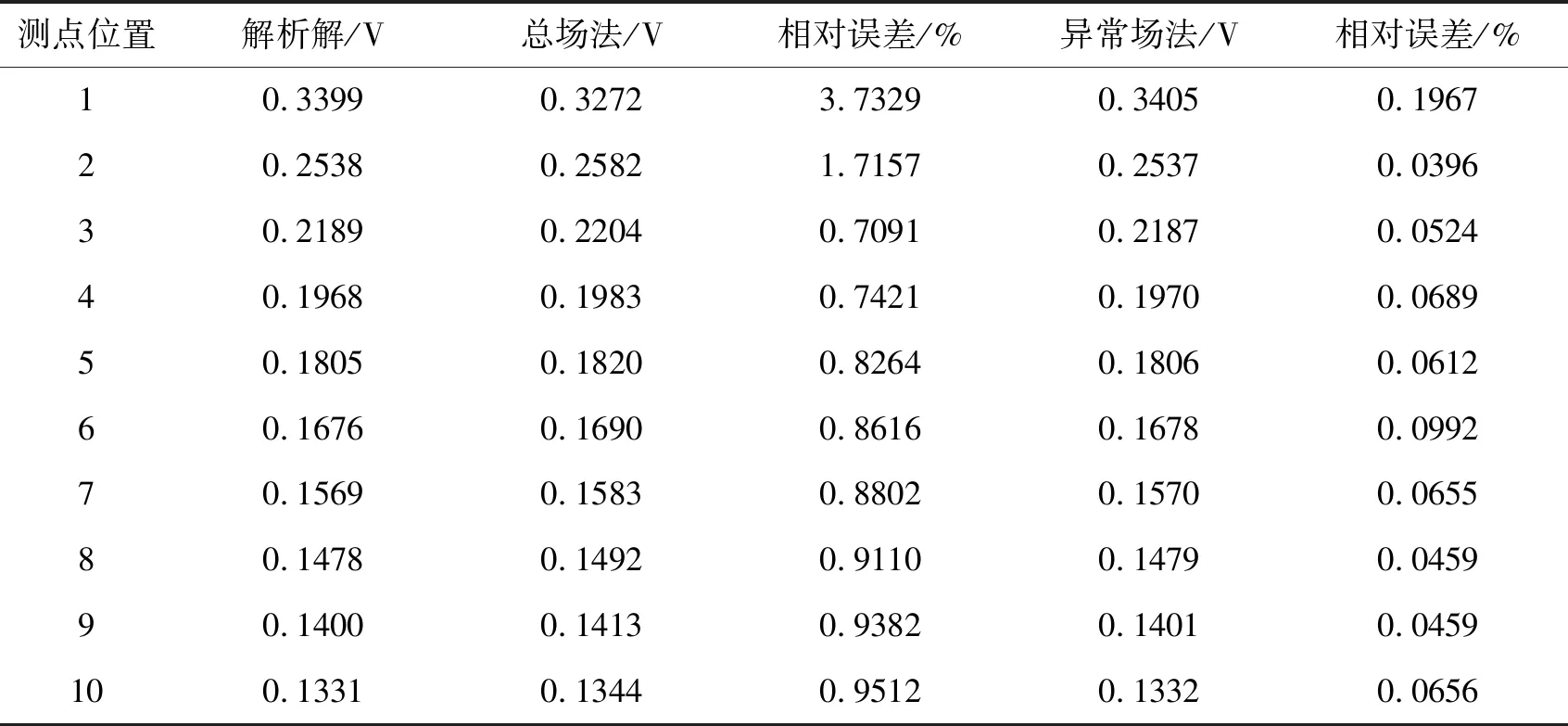
表2 采用7点波数的模拟结果对比
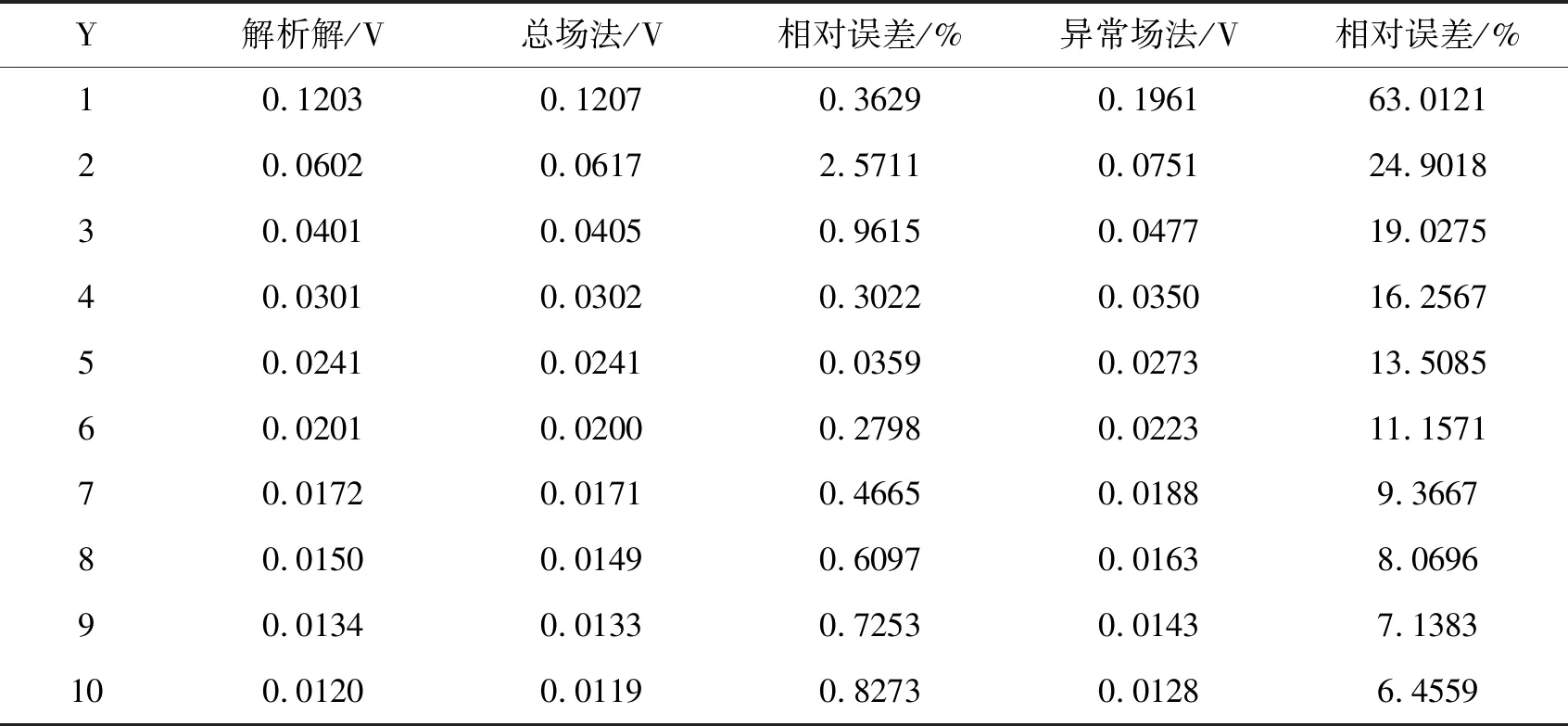
表3 TTI介质模拟结果对比
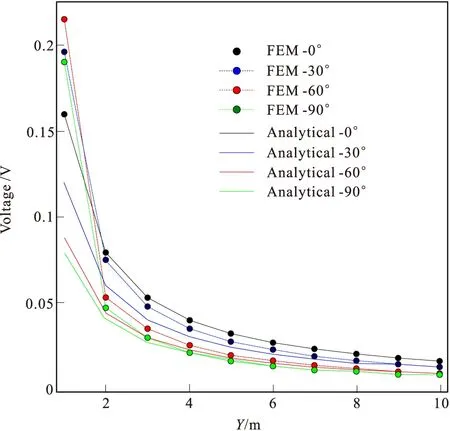
图4 解析解与异常场法数值解曲线
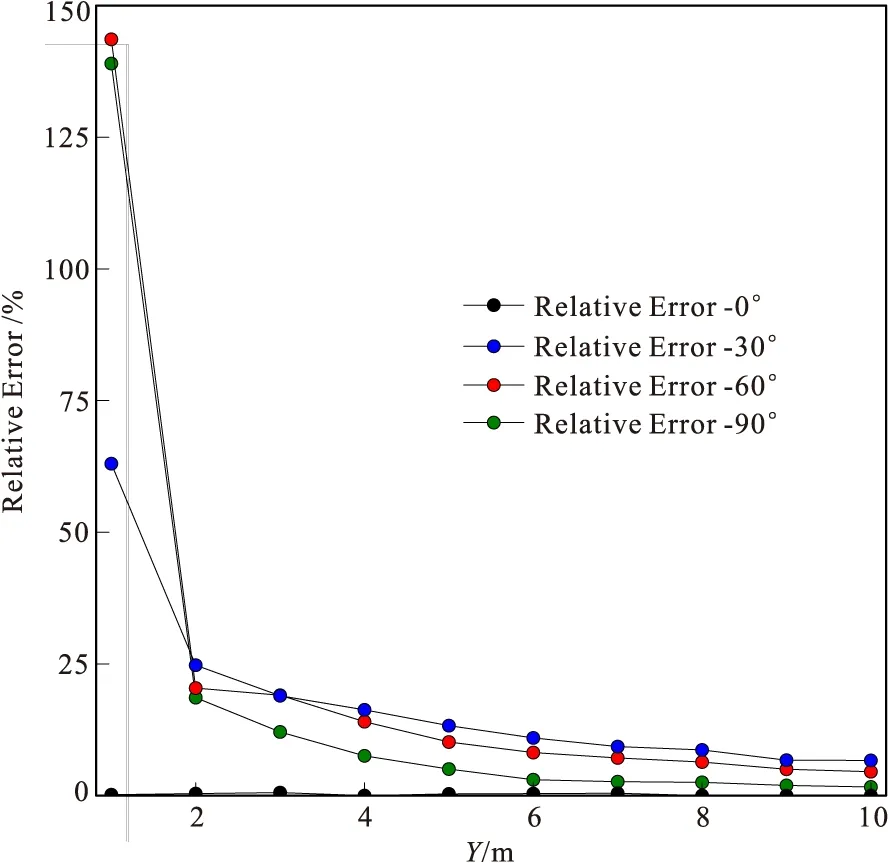
图5 解析解与异常场法数值解相对误差
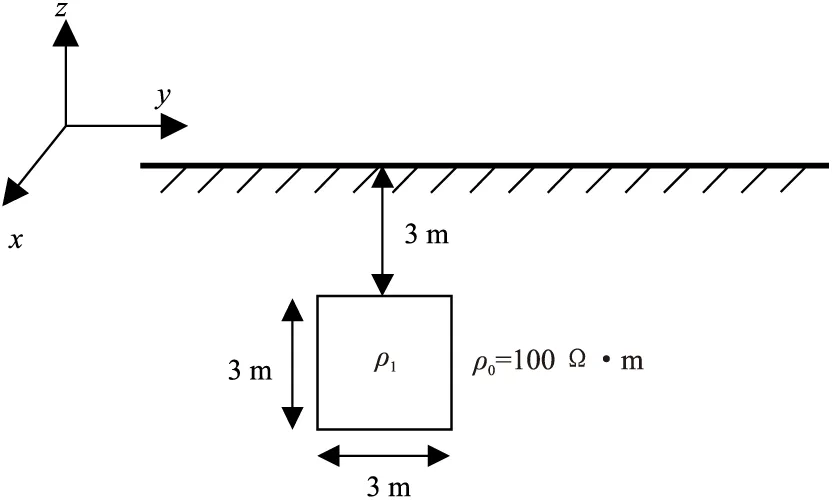
图6 含异常体模型
3.1.3 背景电阻率的取值
采用异常场法简化欧拉角时,假设点源附近的介质与选定坐标系的夹角为零,通过模型来计算当点源处介质为TTI时异常场的结果。
假设均匀半空间,电阻率为ρx=ρy=0.5 Ω·m,ρz=2.0 Ω·m,采用异常场法模拟α=0°、30°、60°、90°的结果,与解析解进行对比验证文中的假设;设置电极为距离点源1 m~10 m且电极距为1 m,10个测量点。
表3给出了α=30°时,总场法与异常场法的解,以及它们与解析解的相对误差,从表3中可以看出,总场法在临近点源的第二个点的误差较大,达到了2.571 1 %,在其他测点处的误差均在1%以内;但异常场法的解误差均较大,在源附近已经达到了63.012 1 %。因为此时背景电阻率的电性主轴与坐标系有α=30°的夹角,不满足文中关于欧拉角的假设,所以此处采用异常场法处理的结果不准确。
设α=0°、30°、60°、90°,解析解与异常场法求解结果的曲线见图4,以及相对误差的曲线见图5。
从以上模拟可以发现点源处的介质如果为TTI介质(背景介质),只能采用总场法进行正演,文中给出的异常场法不再适用。
3.2 含异常体模型
设计如图6所示的含异常体模型,异常体距离地面3 m,大小为3 m×3 m,背景介质为各向同性介质电阻率为ρo=100 Ω·m,在地表进行测量设置40个电极,异常体位于测量区域的中心部分。
设置三个模型,mod1异常体为各向同性电阻率为ρ=10 Ω·m,mod1异常体为各向异性电阻率为ρx=ρy=10 Ω·m,ρz=100 Ω·m,mod3异常体为各向异性,电阻率为ρx=ρy=100 Ω·m,ρz=10 Ω·m。
模拟对称四极装置的响应,取极距AB为3 m、7 m、11 m和21 m的视电阻率曲线进行对比,结果如图7所示。
图7中MD-10、MD-10-100、MD-100-10分别代表mod1、mod2和mod3。
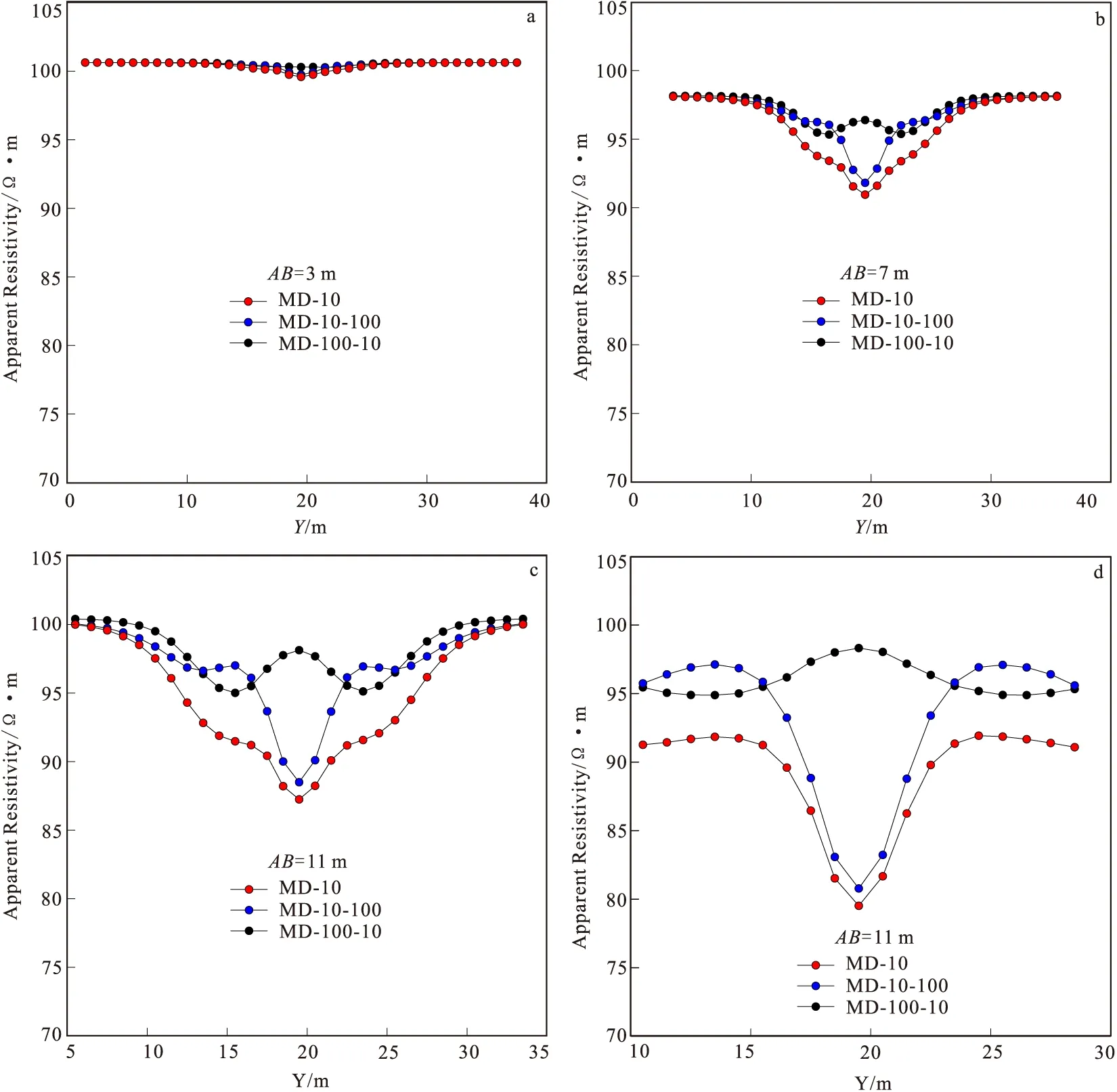
图7 含低阻异常体模型极距为3 m、7 m、11 m和21 m模拟结果曲线图
从图7可以清晰得看出,当极距较小时,对称四极法反映的是较浅介质的电性,所以三个模型的结果相近,均接近100 Ω·m,当极距变大时,受到不同异常体的影响,三个模型的视电阻率曲线出现分离。图7中mod3在四个不同的极距下,视电阻率的值均与背景电阻率较为接近,为100 Ω·m,其异常体的横向电阻率为100 Ω·m,纵向电阻率为10 Ω·m,而mod2模型的模拟结果与异常体为各向同性的 的模拟结果较为接近。对称四极装置、偶极偶极装置以及二极装置的响应,如图8、图9和图10所示。
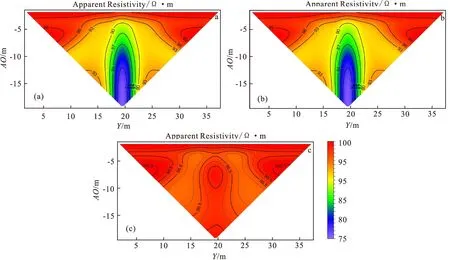
图8 对称四极装置视电阻率剖面
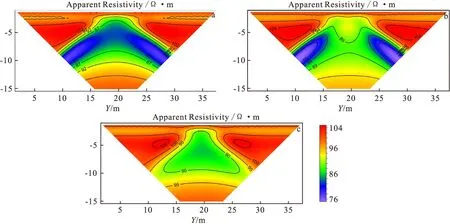
图9 偶极偶极装置视电阻率剖面
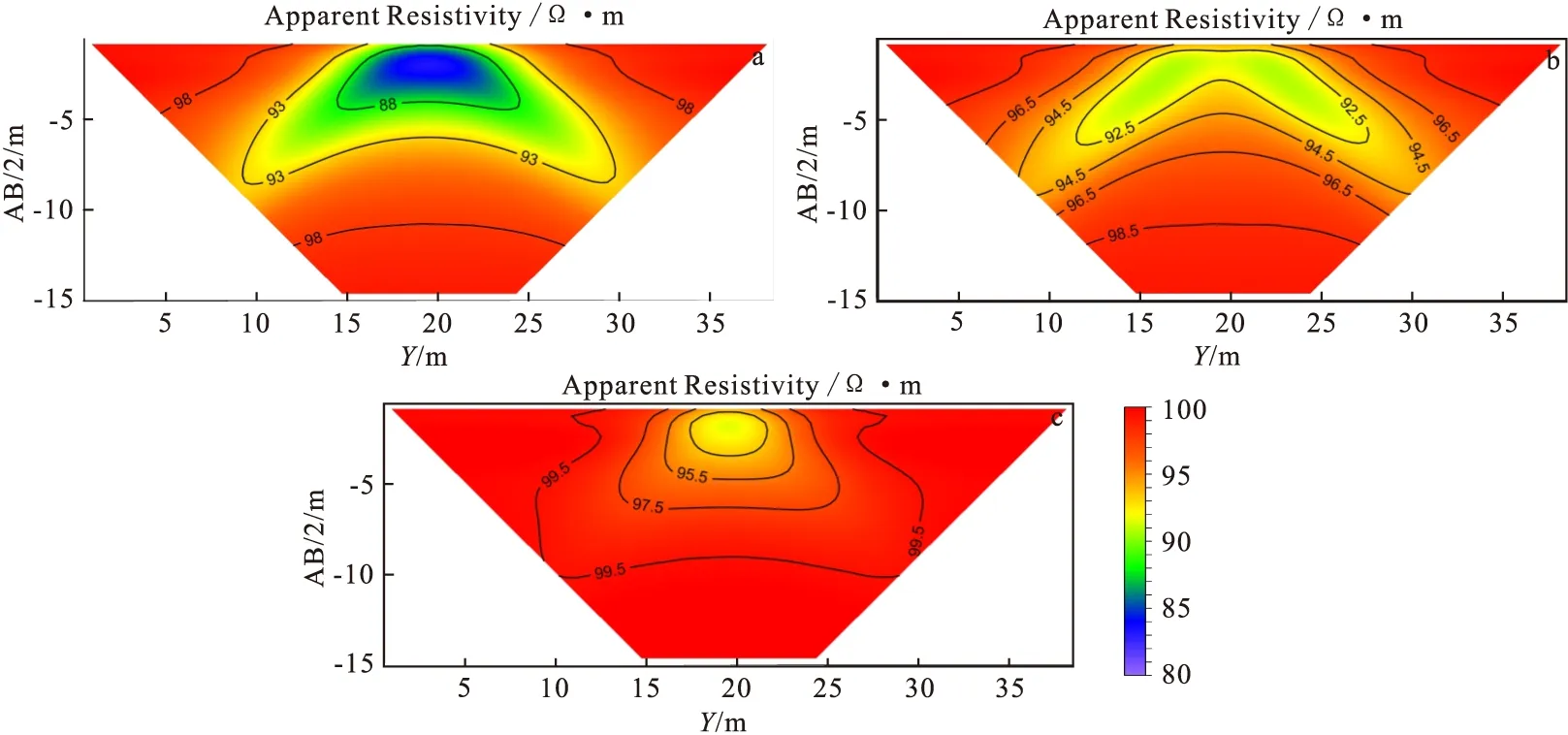
图10 二极装置视电阻率剖面
通过以上模拟,发现介质横向电阻率的变化对测量的结果影响较大,而纵向电阻率对结果影响相对较小。二极和偶极偶极装置相较于三极和对称四极装置,对纵向电阻率的反映更加灵敏,并且对异常的位置和形态反映也更加准确,其中偶极偶极装置对纵向电阻率的变化最为灵敏。
4 结论
我们给出了点源2.5维各向异性异常场法的边值问题和变分问题,并用有限元实现正演模拟。使用异常场法求解时,假设点源附近的介质为VTI介质,简化空间电位解析解的欧拉角,使得异常场法可以进行。
通过算例分析,表明异常场法的精度更高。在模拟计算中,建议地形模型采用5点波数使用总场法,平地形模型使用异常场法7点波数,可以获得更高的精度。
因为使用异常场法时,假设点源附近的介质为VTI介质,所以文中所提出的简化方法并不适合点源附近的介质为TTI的情况,即介质的电性主轴与观测坐标夹角不为0时,该方法并不适合。
通过模拟,发现对于二维介质,直流电阻率法对横向电阻率的变化更为灵敏,而纵向电阻率对结果影响相对较小。

