基于计算量的航迹融合算法性能分析方法
李月武,刘长江,胡建旺,吉 兵,张岐龙
(1.陆军工程大学石家庄校区,河北 石家庄 050000;2.解放军31697部队,辽宁 大连 116104;3.解放军95806部队,北京 100076)
0 引言
信息融合又称数据融合技术,是一个对单个和多个信息源获取的数据和信息进行关联、相关和综合的过程,以获得精确的位置和身份估计[1-2],广泛应用于各个领域。对数据源进行融合时选择不同融合算法会导致不同的融合效果,不同的融合算法也有不同的优点和缺点,文献[3]将算法管理引入到融合的整个过程中,提高了融合效果的有效性和准确性,也对融合系统的性能评估带来便利,可以从系统和模块任一角度出发,进行性能分析。
目前针对航迹融合算法的性能分析,主要是对融合算法进行仿真,分析融合位置误差[4-8],对算法的计算量研究较少,但是有些融合算法是以计算量为代价提高精度,会增加所需信息量,增大计算机开销[4]。位置精度误差是评价融合算法性能的常用指标[9],但计算量也是融合算法的一项重要指标,仅分析位置精度误差,无法全面综合地评价融合算法的性能。
针对航迹融合算法性能分析,一般只考虑融合误差而无法全面评价融合算法的问题,本文提出了一种基于计算量的航迹融合算法性能分析方法。
1 问题描述与模型构建
1.1 问题描述
正如前文所述,目前文献对航迹融合算法性能分析时一般只考虑融合误差,通过剧情设计和计算机仿真得出融合结果,比较融合精度,而不会考虑提高融合精度所带来计算量增加、计算机开销增大的代价,导致在评估算法、选取算法时不能综合考虑算法的性能。
虽然文献[10]从计算量和精度两方面分析算法,但是只是对算法步骤进行了详细的介绍和分析,并没有量化计算量。文献[11]会考虑处理时延来间接评价算法复杂度,但是针对同一算法,不同编程、不同硬件设施会有不同的处理时延,不能从根本上分析算法。文献[12]虽指出鲜有文献对算法运算量进行具体分析,但是该文献只是对算法复杂度进行了简单的分析。文献[13]虽对计算量进行了量化,但是该文献分析的算法不涉及矩阵运算,不适用于航迹融合算法的计算量分析。
本文针对以上问题,提出了以浮点操作数为单位的计算量理论分析方法实现航迹融合算法计算量的量化。
1.2 模型构建
本文针对航迹融合算法进行性能分析,而未针对融合系统,因此不考虑关联精度、丢点率等指标,只考虑计算量和精度两方面。
对航迹融合算法进行性能分析时,不仅要在算法的基础上分析航迹融合算法的计算量,还要对航迹融合算法进行仿真得出误差结果,最后需要建立性能评估模型进行航迹融合算法进行综合评价,评估步骤如图1所示。
由于本文只从两方面对融合算法进行性能评价,且融合算法计算量是确定值,所以本文采用加权法对两个指标进行综合评价,综合评价模型为:
(1)
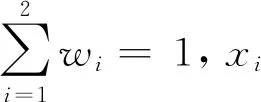
wi为主观赋值,有些融合系统硬件设施较好,对计算量要求较小,便可将计算量的权重设置较小,若硬件设施对计算量要求较高,便可将计算量的权重设置较大些。xi为指标归一化得分,其中误差和计算量都为越小越优型,即
(2)
式(2)中,R为位置误差,Q为计算量。

图1 评估步骤Fig.1 Evaluation step
2 计算量理论分析方法
首先进行航迹融合算法的计算量理论分析,本文以航迹融合算法中常用的简单凸组合融合算法(Covari-ance Convex,CC)和Bar-Shalom-Campo融合算法(BC)两种融合算法为例展开研究[4,14-15]。CC算法和BC算法都可以在不同情况下达到最优,但两者所需的信息量和计算量不同。算法的运行时间不仅与运行设备有很大的关系,并且也会随着不同的算法编程而不同[16]。本节将对算法进行理论分析,以浮点操作数为单位统计原始算法主要步骤的计算量,对计算量进行量化,得到相应的总计算量解析表达式。
2.1 算法分析
在算法计算量理论分析之前,首先简单介绍一下简单凸组合和Bar-Shalom-Campo两种航迹融合算法。
2.1.1 简单凸组合航迹融合算法
简单凸组合航迹融合算法是一种常用的分布式航迹融合算法[15],当不存在过程噪声,且传感器在初始时刻的估计误差不相关时,该算法是最优的[17]。

融合中心对于任意两个传感器之间的航迹估计融合结果为:
(3)
协方差融合方程为:
P=Pi(Pi+Pj)Pj
(4)
对应的信息矩阵形式的表达式为:
(5)
扩展到N>2的情况,假设传感器之间不存在误差的相关性,则融合方程为:
(6)
具体推导过程见文献[15]。
2.1.2BarShalom-Campo航迹融合算法
当航迹的局部估计误差存在相关时,简单凸组合融合算法就不能达到最优,而Bar Shalom-Campo航迹融合算法考虑了各传感器间误差的相关性,可以实现最大似然条件下的最优[7]。
假设航迹间的状态估计误差为:
(7)
则Dij的协方差阵为:
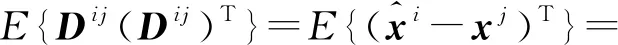
(8)
式(8)中关于Pij和Pji的计算所需资源,可由卡尔曼滤波估计器给出:
(9)
则两个传感器相应的状态融合方程及误差协方差为:
(10)
具体推导过程见文献[15]。
当扩展到传感器数目N>2时,相应的状态融合方程及误差协方差表示为[7,18-19]:
(11)
(12)
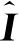
(13)
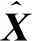
(14)
2.2 计算量分析
根据航迹融合算法的主要步骤,统计计算量,在统计计算量时,遵循以下几个准则[20-23]:
1) 计算量种类归纳为加法运算、赋值运算、乘法运算和除法运算四种;
2) 一次赋值运算相当于一次加法运算;
3) 矩阵运算按元素来进行操作;
为了定量对融合算法的计算量进行分析,采用浮点操作数的方法进行统计。其中,将两个浮点数的加、减、乘或除法运算定义为一次浮点操作数[24]。在算法的实现过程中,有些操作是无法通过简单的加、减、乘、除来实现的,比如矩阵逆运算、矩阵转置运算、指数运算、开方等,可采用相同时间的浮点操作数对其进行等效。下面对一些基本运算的浮点操作数进行说明:
1) 如果A∈Rn×m,B∈Rn×m,则A±B的浮点操作数为n×m;
2) 如果A∈Rn×m,B∈Rn×m,则AB的浮点操作数为2mnl-nl;
3) 如果A∈Rn×n,矩阵A-1的浮点操作数为n3;
4) 如果A∈Rn×m,矩阵AT的浮点操作数为mn;
在对两种算法进行计算量统计时,假设系统中有N个p维传感器跟踪1个目标进行计算量分析,并记计算量为Q。
2.2.1CC算法的计算量分析
CC算法中计算量主要集中在协方差矩阵求逆运算上。
1) 求取协方差融合方程
扩展到N>2的情况,协方差融合方程为:
(15)
根据上面提到的浮点操作数说明,因为有N个p维传感器跟踪1个目标,所以协方差矩阵P为2p阶,则(Pi)-1的浮点操作数为(2p)3,Pi+Pi的浮点操作数为(2p)2,赋值运算相当于加法运算,则为一次浮点操作数,矩阵赋值按元素进行操作为(2p)2,则每进行一次协方差融合运算浮点操作数的解析表达式为:
Q11=(2p)3N+(2p)2(N-1)+(2p)3+(2p)2=
(8p3+4p2)N+8p3
(16)
2) 航迹状态估计融合方程
扩展到N>2的情况,则航迹状态融合方程为:
(17)
Q12=[(2p)3+2(2p)2-2p]N+
2p(N-1)+2(2p)2=
(8p3+8p2)N+8p2-2p
(18)
则简单凸组合融合算法每进行一次总运算计算量以浮点操作数为单位的解析表达式为:
Qcc=Q11+Q12=
(16p3+12p2)N+8p3+8p2-2p
(19)
2.2.2BC算法的计算量分析
BC算法比CC算法更为复杂,因为考虑了传感器之间存在的过程噪声和估计误差之间的互协方差,其中计算量主要集中在求互协方差的运算上。
1) 互协方差运算
(20)
互协方差运算一般应用在两个传感器之间的融合,假设有N=2个传感器,p维传感器跟踪1个目标。所以根据浮点操作数的说明,KH的浮点操作数为8p3-4p2,FPij(k-1)FT的浮点操作数为32p3-4p2,GQGT的浮点操作数为8p3-2p2,赋值运算浮点操作数为(2p)2,此互协方差运算的浮点操作数解析表达式为88p3-2p2,则扩展到N>2个传感器时,协方差运算总计算浮点操作数解析表达式为:
Q21=(88p3-2p2)(N2-N)
(21)
2) 协方差融合方程
(22)
Q22=8p3N3+32p3N2-4p2N+8p3
(23)
3) 航迹状态估计融合方程
(24)
Q23=16p3N3+32p3N2+32p3N+
4p2N+8p3-4p2
(25)
所以Bar-Shalom-Campo融合算法扩展到N>2时,每进行一次总运算计算量以浮点操作数为单位的解析表达式为:
QBC=Q21+Q22+Q23=24p3N3+152p3N2-
2p2N2-56p3N+2p2N+16p3-4p2
(26)
3 仿真实验
本节通过仿真实验验证计算量理论分析的正确性以及对误差进行仿真分析,并通过评估模型对融合算法进行综合评价。仿真时所使用计算机的配置为:CPU intel(R) Core(TM) 2.6 GHz;内存4.00 GB;运行环境Matlab R2012b。本节的各仿真结果都是100次Monte Carlo仿真的均值。
3.1 仿真分析
本小节将通过改变传感器的数量和维数,分别比较在两种情况下CC算法和BC算法的运行时间,验证计算量公式的正确性,并进行仿真分析两种算法的位置误差。
尽管Matlab采用经过优化以后的计算方式,与浮点操作数的计算方式不太一样,仍然可以使用Matlab进行仿真分析,测量算法运行时间与外部条件的关系,用这些结果与计数结果相比较,虽有误差,但在一定程度上可以验证结论的正确性[25-26]。
首先讨论二维的情况,在仿真中取N=2个p=2维雷达传感器,量测误差方差分别为100 m2和150 m2,对10批目标进行跟踪,每1 s跟踪一次,跟踪100次。目标均以vx=100 m/s,vy=200 m/s的速度平行匀速直线运动,初值状态横坐标均为1 000 m,纵坐标分别为[1 000,2 000,3 000,4 000,5 000,6 000,7 000,8 000,9 000,10 000]m,过程噪声方差为100 m2。目标的真实航迹、传感器跟踪航迹以及融合航迹如图2所示,融合误差以及传感器的跟踪位置精度误差,如图3所示。
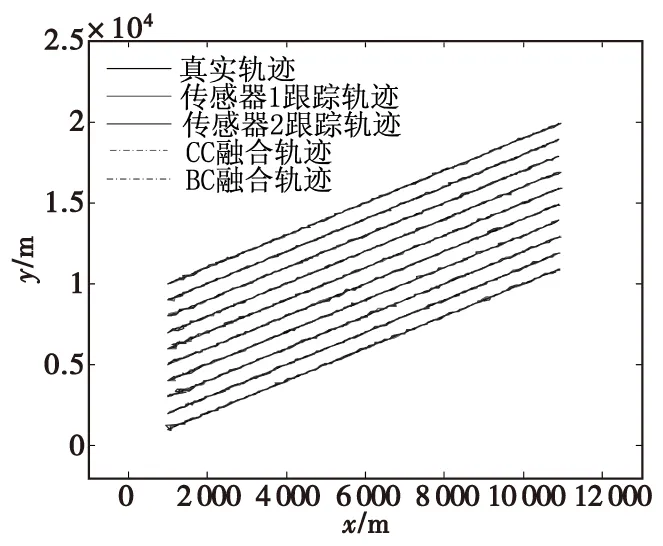
图2 目标轨迹Fig.2 Target track
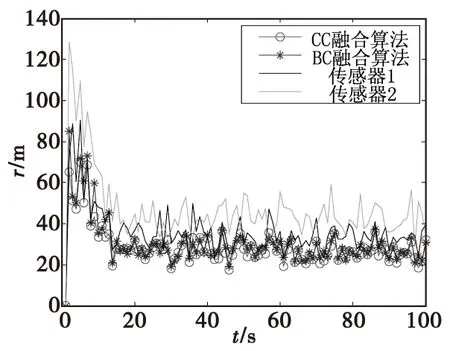
图3 位置精度误差Fig.3 Position accuracy error
为了验证计算量公式的正确性,在同种条件下分别对不同数目N的2维传感器进行仿真,其中一个传感器量测误差方差为100 m2,其余方差全部为150 m2,进行100次Monte Carlo仿真求得均值后,传感器误差均值、CC算法和BC算法的误差和运算时间比值如表1所示。
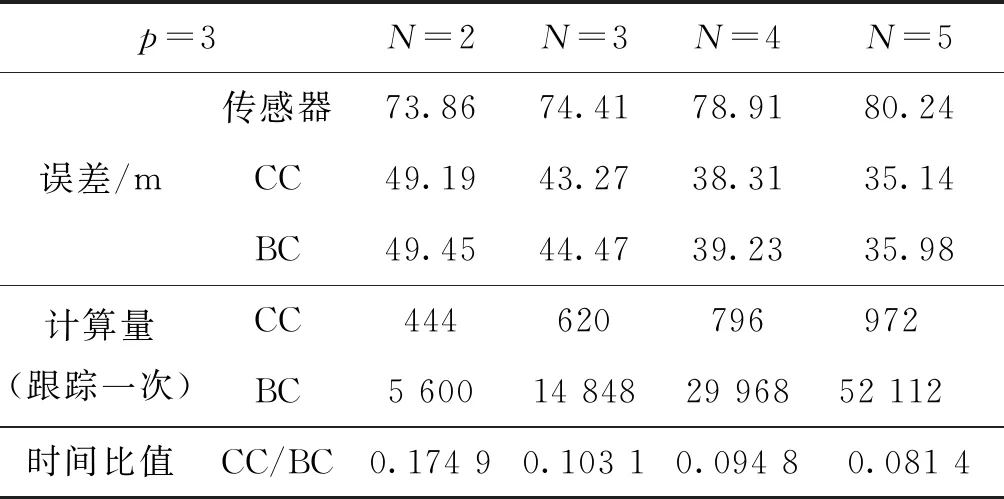
表1 实验数据(情况1)Tab.1 Experimental data (Case 1)
本次仿真讨论三维的情况,在仿真中假设有n=4个目标进行机动运动,取N=3个p=3维传感器对目标进行跟踪,量测噪声分别为100 m2,150 m2和200 m2,四个目标初值状态坐标分别为:[1 000,1 000,1 000],[3 000,3 000,3 000],[-4 000,4 000,2 000],[-4 000,4 000,0],目标1和目标2以vx=100 m/s,vy=200 m/s,vz=10 m/s的速度做匀速直线运动,目标3和目标4分别做机动运动,目标真实轨迹和跟踪状态轨迹以及融合轨迹如图4所示,融合误差以及传感器的跟踪位置精度误差,如图5所示。

图4 目标轨迹Fig.4 Target trajectory
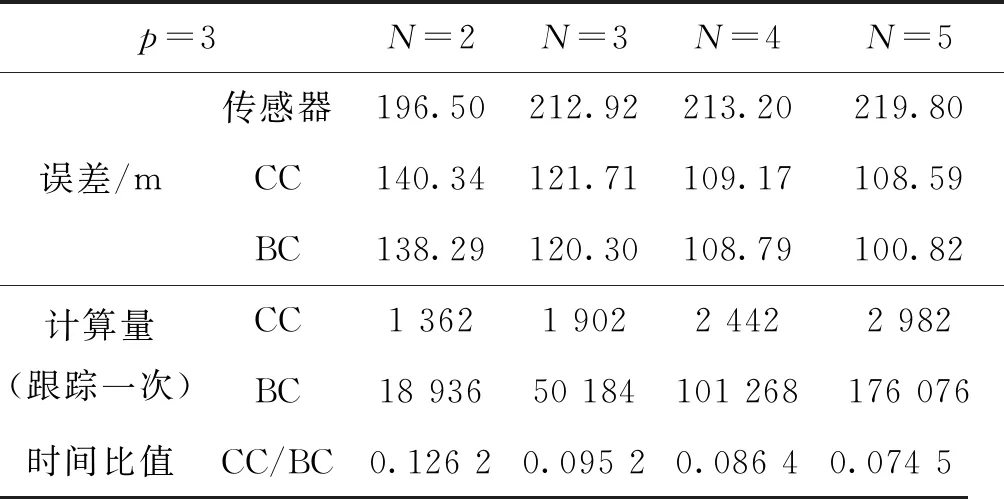
为了证明在此情况下计算量公式的正确性,同样取不同数目N的传感器,其中一个传感器量测误差方差为100 m2,其余方差全部为150 m2的三维传感器进行仿真,其中n=4,进行100次Monte Carlo仿真求得均值后,传感器以及两个融合算法与真值的距离误差均值以及CC算法和BC算法的运算时间比值如表2所示。
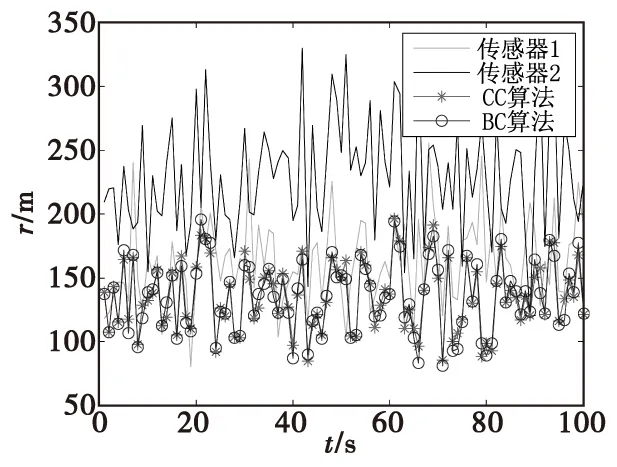
图5 位置精度误差Fig.5 Position accuracy error
p=3N=2N=3N=4N=5误差/m传感器196.50212.92213.20219.80CC140.34121.71109.17108.59BC138.29120.30108.79100.82计算量(跟踪一次)CC1 3621 9022 4422 982BC18 93650 184101 268176 076时间比值CC/BC0.126 20.095 20.086 40.074 5
本小节从两种情况下对简单凸组合融合算法和Bar-Shalom-Campo融合算法进行了仿真分析,可以得出以下结论:
1) 在最小均方误差估计的条件下,CC融合算法和BC融合算法都要优于单个传感器的跟踪效果,在匀速直线运动时,CC算法的融合效果要略优于BC算法,在机动条件下,BC算法的融合效果要略优于CC算法。
2) 在计算量方面,简单凸组合融合算法的计算量要比Bar-Shalom-Campo融合算法低很多,并且随着传感器维数的增加以及传感器数目的增加,计算量差距越来越明显。
3) 运行时间仿真结果与理论分析结果基本一致,虽然由于matlab本身原因,运行时间比值存在一定误差,但在误差允许范围内证明了计算量公式的正确性。
3.2 评估计算
本小节对情况2中N=2,p=3仿真结果进行评估计算,使用评估模型对两种融合算法进行综合评价得出结果。
1) 指标计算
根据越小越优型计算方法,结合实验仿真结果,求得CC算法和BC算法两个指标归一化得分分别为:xCC={0.48,1},xBC={0.58,0}。
2) 设置权重
权重设置具有很强的主观性,根据应用条件和环境进行设置。假如硬件设施对计算量要求较高,便将w2设置较高一些,此处取w1=0.45,w2=0.55。
3) 综合评价
根据2)中假设的背景,使用式(1)中加权法对两种融合算法综合评价得出结果:CC算法得分0.766,BC算法得分0.261,由于对计算量要求较高,且BC算法和CC算法融合精度相差不大,经综合评价得出CC优于BC算法,工程实践中选择CC算法。
4 结论
本文提出了基于计算量的航迹融合算法性能分析方法,该方法通过采用以浮点操作数为单位的方法统计算法主要步骤的计算量进行计算量理论分析,通过计算机仿真进行误差仿真分析,最后通过综合评估模型实现对融合算法的全面评价。仿真实验结果表明,算法运行时间比值在一定误差范围内验证了计算量理论分析的正确性,新的性能分析方法可以有效地评价融合算法性能,为融合算法的性能分析提供参考。

