振动/静电环境下引信安全失效率计算方法

汪仪林，马秋华

(1.西安机电信息技术研究所，陕西 西安 710065；2.机电动态控制重点实验室，陕西 西安 710065)

0 引言

在GJB 373A《引信安全性设计准则》中明确要求“在预定的解除保险和解除隔离流程开始前：防止引信解除隔离或作用的失效率应不大于一百万分之一”；“身管发射的弹药出膛口前：防止引信解除隔离的失效率应不大于一万分之一，防止引信作用的失效率应不大于一百万分之一”；“从启动解除保险和解除隔离流程或身管发射弹药出膛口到安全分离：防止引信解除隔离的失效率应不大于一千分之一。”[1]。

在GJB/Z 29A-2003《引信典型故障树手册》中，给出了多种典型安解系统在勤务处理、发射、安全距离内安全失效率和作用率定量计算结果[2]。随着武器系统发射过载越来越低，电和电磁环境日益复杂，在安全失效率的定量分析中，须计入振动、电和电磁效应的影响，而以往计算中未体现这些因素对安全失效率计算结果的影响，也未提供相应的计算方法，导致安全失效率定量计算不够完善(例如在后坐保险装置设计时，为了有利于解保而将解除的过载设计的过低，在安全失效率计算时，这个门限对计算结果几乎没有影响)，会引起设计偏差，同时会导致在研究中对环境研究的缺失。本文针对此问题，提出了振动/静电环境下对引信安全失效率计算方法。限于篇幅，又不失一般性，只进行解除保险和解除隔离流程开始前安全失效率的计算。

1 典型引信机电安全系统的安全失效率计算

1.1 典型引信机电安全系统

典型机电安全系统原理框图如图1所示。

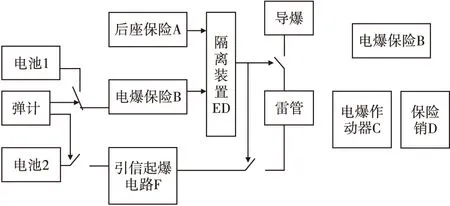
图1 典型引信机电安全系统原理框图Fig.1 The figure of the typical electromechanical fuze safety system

若后坐保险A和电爆保险B是完全独立的，则执行解保流程1；电爆保险需在后坐保险开启的时间窗内解保才能解除保险，则执行解保流程2。

1.1.1 解保流程1

1) 勤务处理时，后坐保险A、电保险装置B将隔离装置E锁定在隔离状态，弹上电源未激活，弹上控制系统、引信电路不工作。后坐保险A为可恢复的弹簧保险装置，电雷管短路机构使电雷管处于短路状态，导弹上的开关1使电爆保险B中的电点火管处于短路状态；

2) 导弹进入不可逆的发射过程，电池1、电池2激活，弹上控制系统工作；

3) 导弹发射，发动机工作、离架后，电爆保险B中的电点火管短路解除，给引信电路供电；

4) 后坐保险机构A在不大于6g的持续的轴向后坐过载作用下解除保险；

5) 导弹飞行至安全距离，弹载计算机向电爆保险B中的电点火管发出点火信号，在火药气体驱动下，电保险装置B解除对回转体的锁定，隔离装置E在扭力簧和钟表机构的作用下运动，解除电雷管短路并逐渐解除隔离。引信处于待发状态。

1.1.2 解保流程2

步骤1)—步骤3)同流程1；

4) 后坐保险机构A在不大于6g的持续的轴向后坐过载作用下解除保险，并开启时间窗；

5) 导弹飞行至安全距离，弹计向电爆保险B中的电点火管发出点火信号，在火药气体驱动下，电保险装置B解除对隔离装置E的锁定，此时，若在后坐保险保持在解保状态或在开启的时间窗内，隔离装置E在扭力簧和钟表机构的作用下运动，解除电雷管短路并逐渐解除隔离；若在后坐保险开启的时间窗外，无法解除隔离，引信处于安全状态。

1.2 典型机电安全系统解保流程开始前安全失效率计算

解保流程开始前，解除隔离的概率P11的计算见式(1)。

P11=P(A11B11)+P(E11)=
P(B11|A11)+P(A11|B11)+P(E11)

(1)

式(1)中，P(A11B11)为后坐保险和电爆保险均解除的概率；P(B11|A11)为后坐先于电爆保险失效的概率；P(A11|B11)为电爆保险先于后坐失效的概率；P(E11)为隔离机构隔爆失效的概率，其值取为：P(E11)=3×10-7。

由于后坐保险和电爆保险的解除为相互独立的事件，则：

P(B11|A11)+P(A11|B11)=P(B11)×P(A11)

(2)

式(2)中，P(A11)为解保流程开始前后座保险A失效的概率；P(B11)为解保流程开始前电爆保险B失效的概率。

1.2.1 解保流程1开始前解除隔离的概率计算

式(1)可以写为：

P11=P(B11)×P(A11)+P(E11)=
P(a1)×[P(c1)+p(d1)+P(z1)]+P(E11)

(3)

式(3)中，P(a1)为后坐保险件不能将隔离装置锁定在隔爆位置的概率，其值取为：P(a1)=7×10-4；P(c1)为电做动器自作用的概率，其值取为P(c1)=5×10-5；P(d1)为电爆保险件不能将隔离装置E锁定在隔爆位置的概率，其值取为：P(d1)=10-3；P(z1))为弹计给出错误控制信号导致电爆保险解除的概率，其值取为P(z1)=0.5×10-3。

解保流程开始前解除隔离的概率P11计算：

P11=7×10-4×(5×10-5+10-3+0.5×10-3)+
3×10-7=1.55 ×7×10-7+3×10-7=
13.85×10-7

1.2.2 解保流程2开始前解除隔离的概率计算

解保流程2必须后坐保险先于电爆保险解除才能解除隔离，因此式(1)改为式(4)：

P11=P(B11|A11)+P(E11)

(4)

后坐保险先于电爆保险失效和后坐保险后于电爆保险失效概率各为P(A11B11)/2，即：P(B11|A11)=P(A11|B11)=P(B11)×P(A11)/2。

代入式(3)，式(4)则有：

P11=P(B11|A11)+P(E11)=
P(a1)×[P(c1)+p(d1)+P(z1)]/2+P(E11)

(5)

P11=1.55×7×10-7/2+3×10-7=8.425×10-7

很明显，对保险件解除有顺序要求时，具有更高的安全性。

2 振动/静电环境下引信安全失效率计算方法

2.1 静电环境对引信安全失效率影响的计算方法

考虑静电的影响将式(5)改写为式(6)：

P11=P(B11|A11)+P(E11)=P(a1)×
[P(c1)+P(c2)+P(d1)+P(z1)]/2+P(E11)

(6)

式(6)中，P(c2)为电爆做动器在电和电磁环境下意外作用的概率。

P(c2)的计算方法：

设静电放条件下电爆作动器作用概率Pe见式(7)：

Pe=1-exp (-E/2)

(7)

式(7)中，E为施加到电爆保险件归一化电能。

按照GJB 373A的要求，最大不作用能量Em的定义为Pe=0.001对应的能量，即：

0.001=1-exp(-Em/2)

(8)

求得，Em=0.002。

设计考虑人体静电，并按照GJB 786《预防电磁场对军械危害的一般要求》规定，留有约16.5 dB(0.022 5倍)的裕量[3]，对应的作用概率为：P(c2)=1-exp(-Em×0.022 5/2)=2.25×10-5

将计算结果代入式(6)，则有：

P11=7×10-4×(5×10-5+10-3+2.25×10-5+
0.5×10-3)/2+3×10-7=1.572 5×7×10-7/2+
3×10-7=8.504×10-7

略高于式(5)的计算结果，若设计裕量不够时，则可能不满足要求。

2.2 振动对引信安全失效率的影响的计算方法

考虑振动的影响将式(5)改写为式(9)：

P11=P(a1)×[P(c1)+P(z1)+P(d1)]/2+
P(a2)×[P(c1)+P(z1)+P(d1)]+P(E11)

(9)

式(9)中，P(a2)为运输振动环境下后坐保险装置处于解保状态并开启有效时间窗的概率。

P(a2)的计算方法：

根据振动环境的功率谱，由功率谱可产生的随机过程作为后坐保险的激励，统计此激励下后坐保险解除次数和每次解保的持续时间，计算P(a2)的数值。

为了方便，以某直升机挂飞振动为例加以说明。

图2(a)为某直升机挂飞的振动谱，根据谱产生随机过程如图2(b)所示；计算振动条件下，120 h内过载超过6g，不同持续时间的次数列于表1。

图2 某典型直升机的振动谱图及其随机过程图Fig.2 The vibration spectrum and randomize process of the typical helicopter

宽度t/ms次数Nmi=Ni-Ni+1≥281 96380 557≥3140 6139 6≥41010≥500≥600

由于振动时，后坐保险处于运动状态，设后坐保险解除并开启时间窗的条件为：过载不小于6g、持续时间不小于3 ms，过载小于6g后坐保险件恢复，考虑保险件之间和隔爆件之间的运动关系，对应时间窗宽为6 ms；若电爆保险在时间窗内解除，则解除对隔爆件的锁定，隔离装置在扭力簧和钟表机构的作用下运动，解除电雷管短路并逐渐解除隔离；若电爆保险在时间窗外解除，则不能解除保险，引信处于安全状态。

若振动过载大于6g的宽度为3 ms，时间窗t3=6 ms；若振动过载大于6g的宽度为4 ms，时间窗t4=7 ms；依此类推。

由表1数据计算P(a2)：

P(a2)=[m3×t3+m4×t4]/T

(10)

式(10)中，T为挂飞时长，120 h=432×106ms。P(a2)=[1 396×6+10×7]/432 ×10-6=19.6×10-6。

代入式(9)：P11=1.55×10-3×(7×10-4/2+19.6×10-6)+3×10-7=5.73×10-7+3×10-7=8.73×10-7，满足GJB373A安全失效率的要求。

考虑后坐保险解除的过载存在散布，若有5%的后坐保险在2 ms持续过载下即可解除，式(10)则可写为：

P(a2)=[m3×t3+m4×t4]/T×0.95+
m2×t2×0.05/T

由表1数据算得：

P(a2)=19.6×10-6×0.95+80 557×5/432×10-6×0.05=
110.8×10-6

代入式(9)：

P11=[P(a1)/2+P(a2)]×
[P(c1)+P(z1)+P(d1)]+P(E11)=
1.55×10-3×(7×10-4/2+110.8×10-6)+3×10-7=
7.14×10-7+3×10-7=10.14×10-7

几乎不满足GJB373A安全失效率的要求,所以为地面武器系统设计的安全系统，在机载条件下的适应性，需要仔细评估。

3 不同平台及解保条件下引信安全失效率计算

3.1 空中补给静电环境对引信安全失效率的影响

若要将为地面武器设计的安全系统用于直升机载武器，则需要考虑空中补给的静电影响。根据GJB 573A《引信环境与性能试验方法》的方法601静电放电试验的要求[4]，人体静电能量Erm按25 kV、500 pF电容储能计算，直升机空中补给的静电能量Ezm按300 kV、1 000 pF电容储能计算。

电容储能计算：

E=qV=cV2

(11)

式(11)中，q为电容的电荷量；V为电容上的电压。

将人体静电和直升机空中补给静电电压和电容值代入式(11)，则有：

人体静电能量为：

Erm=(25×103)2×500×10-12=0.312 5 J

直升机空中补给的静电能为：

Ezm=(300×103)2×1 000×10-12=90.0 (J)

原设计为人体静电并留有16.5 dB的裕量，而10×lg(Ezm/Erm)=24.5 dB，即原16.5 dB的裕量则变为：16.5-24.5=-8 dB，即式(8)计算的最大不作用能量的6.3倍。

代入式(7)，电爆保险作用概率P(c2)=1-exp(-0.002×6.3/2)=6.3×10-3。

代入式(6)：

P11=7×10-4×(5×10-5+10-3+6.3×10-3+
0.5×10-3)/2+3×10-7=55.3×10-6

不满足GJB 373A对安全失效率的要求。

3.2 不同直升机挂飞振动对引信安全失效率的影响

不同型号直升机振动谱不同，按照GJB 150A.16《军用装备实验室环境试验方法第16部分：振动试验》的振动条件[5]，计算振动环境对安全失效率的影响。

图3(a)为GJB 150A.16中直升机挂飞的振动谱，图3(b)为利用该谱产生随机过程。计算振动条件下，120 h内后坐过载超过6g，不同持续时间的次数，将结果列于表2。

图3 某典型直升机的振动谱图及其随机过程图Fig.3 The vibration spectrum and randomize process of the typical helicopter

宽度t/ms次数Nmi=Ni-Ni+1≥3514 003465 441≥448 56247 333≥51 2291 222≥677≥700

后坐保险解除和开窗宽度同2.2节，则有：

P(a2)=[m3×t3+m4×t4+m5×t5+m6×t6]/T=
[465 441×6+47 333×7+1 222×8+7×9]/432×10-6=
3 133 816/432×10-6=7.25×10-3

代入式(9)：

P11=(7×10-4/2+7.25×10-3)×1.55×10-3+3×10-7=
7.6×10-3×1.55×10-3+3×10-7=12.08×10-6

明显不满足GJB 373A安全失效率的要求。

3.3 解保阈值及持续时间对引信安全失效率的影响

为了方便讨论，将图3振动谱过载超过7g，持续时间大于3 ms的次数列于表3；过载超过8g，持续时间大于3 ms的次数列于表4；过载超过9g，持续时间大于3 ms的次数列于表5。

表3 120 h内挂飞振动过载超过7 g且不同宽度的次数Tab.3 The number of overload which is more than 7 g at different duration in 120 hours vibration process

表4 120 h内挂飞振动过载超过8 g且不同宽度的次数Tab.4 The number of acceleration of gravity more than 8 gat different duration in 120 hours vibration process

表5 120 h内挂飞振动过载超过9 g且不同宽度的次数Tab.5 The number of acceleration of gravity more than 9 g at different duration in 120 hours vibration process

3.3.1后坐保险解除并开启时间窗的条件为过载为7～9g、持续3 ms的安全失效率计算

若坐保险解除并开启时间窗的条件为：过载7g、持续4 ms，由表3算得：

P(a2)=(m3×t3+m4×t4+m5×t5+m6×t6)/T=
(124 936×6+4 674×7+20×8)/432×10-6=
1.81×10-3

代入式(9)：

P11=(7×10-4/2+1.81×10-3)×1.55×10-3+
3×10-7=3.65×10-6

若坐保险解除并开启时间窗的条件为：过载8g、持续4 ms，由表4算得：

P(a2)=(m3×t3+m4×t4+m5×t5+m6×t6)/T=
(20 230×6+243×7+1×8)/432×10-6=
0.285×10-3

代入式(9)：

P11=(7×10-4/2+0.285×10-3)×1.55×10-3+
3×10-7=1.28×10-6

若坐保险解除并开启时间窗的条件为：过载9g、持续4 ms，由表5算得：

P(a2)=(m3×t3+m4×t4+m5×t5+m6×t6)/T=
(1 786×6+10×7)/432×10-6=0.025 0×10-3

代入式(9)：

P11=7×10-4/2+0.025×10-3)×1.55×10-3+
3×10-7=0.863×10-6

后坐保险解除并开启时间窗的条件为：过载为9g、持续3 ms，可满足安全失效率的定量要求。

3.3.2后坐保险解除并开启时间窗的条件为过载为6～8g、持续4 ms的安全失效率计算

若坐保险解除并开启时间窗的条件为：过载6g、持续4 ms，由表2算得：

P(a2)=(m4×t4+m5×t5+m6×t6)/T=
(47 333×7+1 222×8+7×9)/432×10-6=
0.790×10-3

代入式(9)：

P11=(7×10-4/2+0.79×10-3)×1.55×10-3+
3×10-7=2.07×10-6

若坐保险解除并开启时间窗的条件为：过载7g、持续4 ms，由表3算得：

P(a2)=(m4×t4+m5×t5+m6×t6)/T=
(4 674×7+20×8)/432×10-6=0.076 1×10-3

代入式(9)：

P11=(7×10-4/2+0.076 1×10-3)×1.55×10-3+
3×10-7=0.96×10-6

后坐保险解除并开启时间窗的条件为：过载7g、持续4 ms，可满足安全失效率的定量要求。

若坐保险解除并开启时间窗的条件为：过载8g、持续4 ms，由表4算得：

P(a2)=(m4×t4+m5×t5+m6×t6)/T=
(243×7+1×8)/432×10-6=3.96×10-6

代入式(9)：

P11=(7×10-4/2+3.96×10-6)×1.55×10-3+
3×10-7=0.847×10-6

后坐保险解除并开启时间窗的条件为：过载8g、持续4 ms，安全失效率与原设计相当。

3.3.3后坐保险解除并开启时间窗的条件为过载6g、持续5 ms的安全失效率计算

由表2算得：

P(a2)=(m5×t5+m6×t6)/T=
(1 222×8+7×9)/432×10-6=0.022×10-3

代入式(9)：

P11=(7×10-4/2+0.022×10-3)×1.55×10-3+
3×10-7=0.878×10-6

后坐保险解除并开启时间窗的条件为：过载6g、持续5 ms，可满足安全失效率的定量要求。

上述计算表明，图3所示振动谱的挂飞振动条件下，后坐保险启动阈值提高，可以降低安全失效率。当阈值提高至9g时，可满足安全失效率的定量要求；增加解保过载所需的持续时间，是更为有效的降低安全失效率的技术途径，后坐解保过载持续时间由3 ms增至5 ms，可满足安全失效率的定量要求；现有设计中为了提高解保可靠性，往往把后坐启动过载设置较低，安全失效率有可能不满足GJB 373A《引信安全性设计准则》中“在预定的解除保险和解除隔离流程开始前：防止引信解除隔离或作用的失效率应不大于一百万分之一”的要求。为了保证解保可靠性而不得不设置较低的启动过载时，应提高过载持续时间，以确保在可能经历的环境下仍具有较高的安全性。

4 结论

本文提出了静电、振动环境下引信安全失效率计算方法，该方法通过指数概率计算、振动谱随机过程统计计算得到静电放电、运载平台等可信环境下的安全失效率，及解除后坐保险不同过载阈值和持续时间下的安全失效率。计算表明，在解除保险过程中有顺序要求时，有利于满足安全失效率的定量要求；适应地面静电要求的引信机电安全系统上机后，有可能不满足安全性要求；引信配用同样弹药用于不同载体时，因载体的振动谱不同而对引信安全失效率产生不同影响，需仔细审核引信安全性；引信安全系统的后坐保险不能一味降低解保过载，在不得不降低解保过载时，应增加过载持续时间，并根据可信环境复核安全失效率的计算结果。