MEMS陀螺仪加速参数退化的可靠度评估

刘 吉，于丽霞,武锦辉

(1.中北大学信息与通信工程学院，山西 太原030051；2.中北大学仪器与电子学院 ，山西 太原030051)

0 引言

MEMS陀螺仪广泛应用于航空、航天、国防等领域，其在应用过程中的质量和可靠性要求越来越高，而衡量器件可靠性重要指标的可靠度评估问题备受关注，尤其是如何采用高效准确的可靠性试验与评估方法得到符合MEMS陀螺仪原理、敏感结构尺寸、加工工艺及工作规律的可靠度指标[1-3]。

以失效时间为依据的可靠度评估方法只利用了样本的正常和失效两种状态，忽视了退化过程的微观变化；基于性能退化的可靠度评估方法试验时间足够长，试验样本数量足够多，否则对样本可靠度做统计推断的精度较差[4-5]。针对此问题，本文提出了MEMS陀螺仪加速参数退化的可靠度评估方法。

1 MEMS陀螺仪结构及退化评估方法

本文研究的MEMS陀螺仪基于静电驱动、电容检测原理，结构如图1所示，其中角速率敏感元件是核心部分，主要由驱动模块、微结构和检测模块组成。描述MEMS陀螺仪特性的参数有很多，其中零偏易于稳定测量又能客观反映样本的工作状态，是应用领域关注的最基本参数，因此选择零偏作为加速退化试验的特征参数[6]。

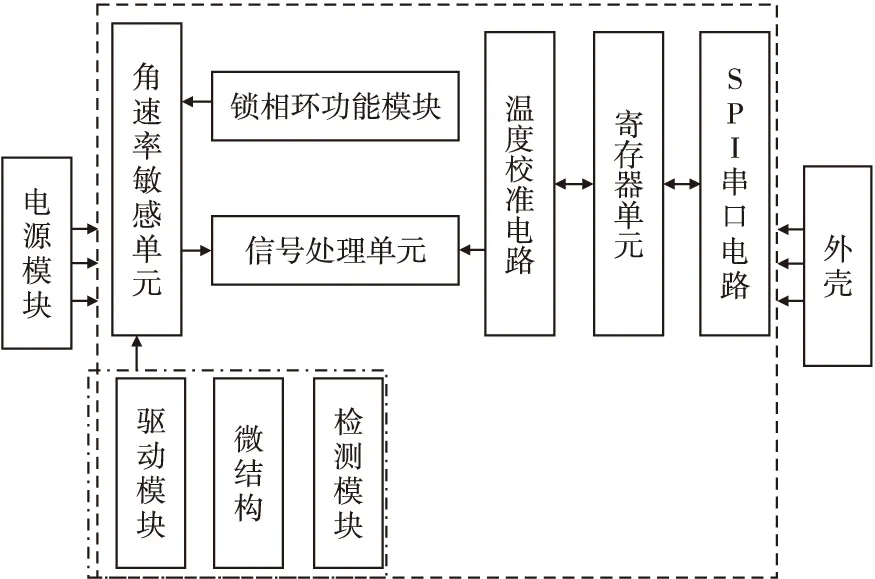
图1 MEMS陀螺仪组成结构框图Fig.1 Principle diagram of MEMS gyroscope

MEMS陀螺仪在实际应用环境中常伴随高温、温变、瞬态高温等恶劣环境，而制作芯片的硅材料受温度变化影响显著, 不但结构尺寸发生变化，而且弹性模量、残余应力等性能也会变化，从而导致器件失效，造成测试弹体信息的精确度下降。为快速得到样本失效敏感参数退化量与温度的关系，采用加速恒定步进应力的加载方式，最高应力不能大于该样本结构材料、制造工艺所能承受的极限应力，且保证不同应力下退化失效机理一致。依据阿伦尼斯模型，确定尺度参数与应力的关系，利用试验数据计算加速参数，从而得到可靠度指标[7-8]。

2 加速参数退化的可靠度评估方法

加速参数退化可靠度评估的核心是合理建立参数退化模型和相关参数的加速模型。建立参数退化模型包括基于退化轨迹拟合和基于退化量分布拟合，其流程如图2和图3所示[9-10]。

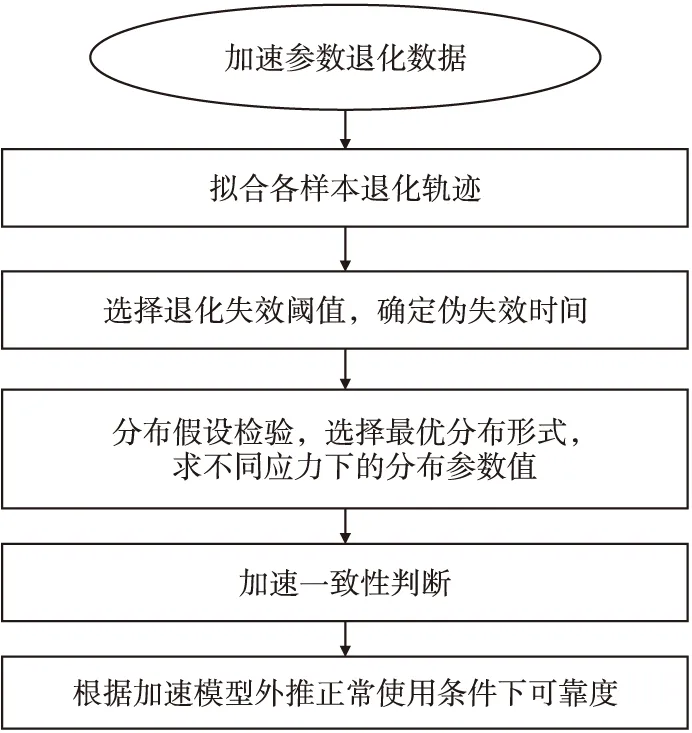
图2 加速退化轨迹评估流程Fig.2 Assessment process accelerated degradation distribution

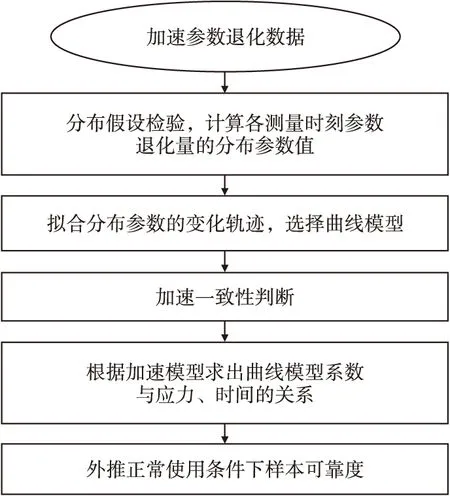
图3 加速退化量分布评估流程Fig.3 Assessment process accelerated degradation distribution

基于退化轨迹拟合的方法根据各样本的加速参数退化趋势，选择适当的退化轨迹模型；根据应用需求，选择退化失效阈值，确定伪失效时间；对伪失效时间分布假设检验，选择最恰当的分布形式，估计分布参数；通过加速一致性判断，选择加速模型求出分布参数与应力的关系；外推正常使用条件下样本的总体参数及可靠度参量函数。

基于退化量分布拟合的方法是对多个样本在不同测量时刻的退化量分布规律进行建模，能够反映出参数退化量的统计特征随时间的变化规律。其主要思路是对各个测量时刻的退化数据分布假设检验，计算各个时刻参数退化量的分布参数估计值；拟合分布参数随时间的变化规律，选择曲线模型，求出各应力水平下曲线模型系数；通过加速一致性判断，选择加速模型，求出曲线模型与应力水平的关系；根据加速方程，求正常应力下满足退化失效阈值时样本的分布参数随时间的函数关系，从而得到可靠度函数。

3 MEMS陀螺仪加速参数退化可靠度评估验证实验

本文对15个MEMS陀螺仪样本开展了加速参数退化试验，图4是根据样本在三组高温应力(T=70 ℃,100 ℃,120 ℃)下加速退化试验中零偏值变化情况绘制的退化轨迹，结合应用背景，假设该样本的退化失效阈值是增加3% (即Df=3)，正常工作温度为T0=25 ℃。应用上述加速参数退化的可靠度评估方法对其进行可靠度评估。

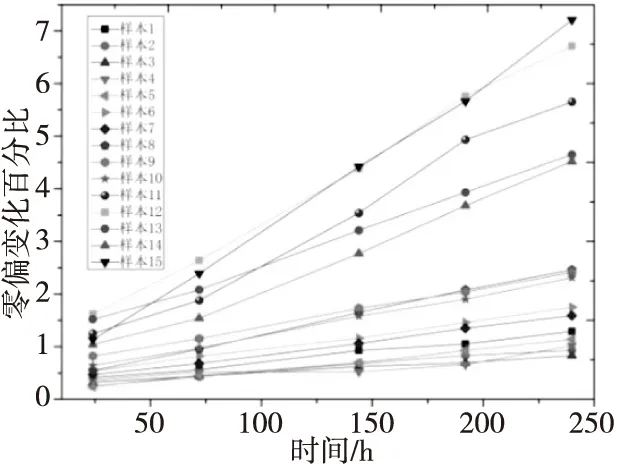
图4 不同应力下样本的参数退化轨迹Fig.4 Parameter degradation traces of samples under different stresses

3.1 基于退化轨迹的拟合方法

根据图4估计所有应力水平下所有样本的退化轨迹模型参数，外推每个样本到达退化失效阈值的时间，并分布假设检验，结果如图5所示。三个应力下假设检验AD统计量值分别为2.48，2.683，2.4(Weibull分布)，2.357，2.511，2.332(正态分布)。Weibull分布适应性较好，正态分布计算相对简单。因此应用两种分布形式的统计分析方法对所得到的退化伪失效时间分析。

图5 不同应力下退化伪失效时间的分布假设检验Fig.5 Distribution hypothesis test of degenerate pseudo-failure time under different stresses

3.2 基于退化量分布的拟合方法

对不同温度应力，不同测量时刻的参数退化量分布假设检验，结果如图6所示，不同时刻样本退化量基本服从正态分布和Weibull分布，且不同时刻所服从的Weibull分布形状参数m近似相等。

服从正态分布时，均值与均方差随时间的变化曲线如图7所示，在不同温度应力下参数退化量的均值与均方差是时间的线性函数，且求得的方程系数随应力增加而增加。

假设样本参数退化量均值与均方差方程系数与温度的关系满足Arrhenius加速模型，分布参数与时间、温度的关系为：

图6 不同温度应力，不同测量时刻参数退化量分布假设检验图Fig.6 Hypothesis test chart of parameter degradationdistribution under different temperature stress and measurement time

图7 不同温度应力下参数退化量均值与均方差曲线Fig.7 Mean and mean square error of parameter degradation under different temperature stresses

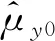
服从Weibull分布时，尺度参数与形状参数随时间的变化曲线如图8所示。尺度参数是时间的线性函数，且方程系数随应力增加而增加，形状参数随应力增加而减少。

假设样本参数退化量尺度参数方程系数及形状参数与温度的关系满足Arrhenius加速模型，建立相应的加速方程，并求得分布参数与时间、温度的关系：

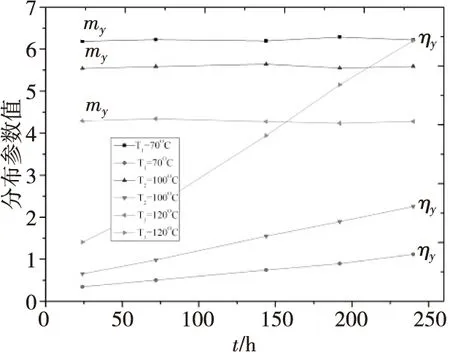
图8 不同温度应力下尺度参数与形状参数曲线(m：形状参数；η：尺度参数)Fig.8 The parameter of scale and shape under different temperature stress

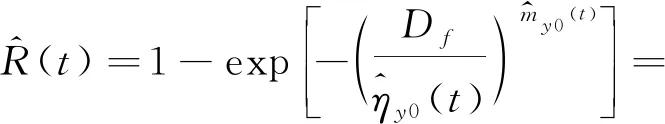
图9是可靠度评估曲线，基于退化轨迹的拟合方法过程简洁易懂，两条曲线形状接近，服从正态分布的评估结果较保守(曲线偏左)，与假设检验结果中正态分布统计量值较小一致。基于退化量分布拟合的方法反映了退化参数所服从分布形式的参数随时间与温度应力的变化情况，能够更准确的反映样本的实际退化情况。

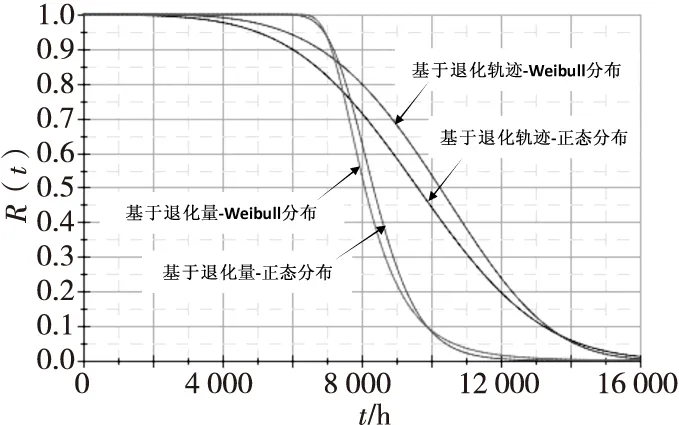
图9 不同评估方法得到的MEMS陀螺仪可靠度曲线Fig.9 MEMS gyroscope reliability curve obtained by different evaluation methods

4 结论

本文提出了MEMS陀螺仪加速参数退化的可靠度评估方法。该方法首先对样本的结构特点和表征性能退化的特征参数、敏感应力及加载方式进行了理论分析，然后形成了基于退化轨迹拟合和退化量分布拟合两种方式的加速参数退化可靠度评估方法，应用其流程对15个MEMS陀螺仪样本开展了加速退化试验，通过对试验数据分布假设检验，选择恰当的分布形式计算分布参数并验证退化失效机理的一致性，最后利用建立的加速模型评估样本在正常使用环境中的可靠度。通过对比实验结果表明，退化轨迹拟合方法过程简洁易懂，退化量分布拟合方法建立了分布参数与时间和应力的关系，体现了样本参数退化之间的差异性，能够反映MEMS陀螺仪在温度应力下退化的实际情况，其结果相对退化轨迹的拟合方法准确度更高，因此可促进可靠度指标对样本实际研制工作的指导。