基于GAN的半监督低分辨雷达目标识别算法

朱克凡，王杰贵，吴世俊

(1.国防科技大学电子对抗学院，安徽 合肥 230037；2.中国人民解放军96713部队，江西 上饶 334100)

0 引言

雷达目标识别(Radar Target Recognition，RTR)是雷达研究的一个重要方向。由于高分辨雷达研究成本高、周期长、难以普及，现役雷达大部分是低分辨雷达，且随着脉冲压缩技术的普及，传统低分辨雷达也能拥有很高的径向分辨力，能够提取目标一维距离像等细微特征，基于低分辨雷达的目标识别技术研究仍然是雷达研究的一个重要热点[1-4]。

在现代战争中，当雷达的脉冲重复频率较低或者目标是先进的非合作目标或隐身目标时，通常难以获取足够多的训练样本[5]。在进行雷达侦察任务时，采集到大量无标签数据，对其进行半监督学习能够有效提高目标识别率。目前，对于雷达目标的半监督学习方法主要是基于支持向量机(Support Vector Machine, SVM)。文献[6]基于信号调制谱特征利用多核直推式支持向量机(TSVM-MKL)算法实现了对飞机目标的分类。文献[7]基于信号RCS特征通过TSVM-MKL算法实现了对弹道目标的分类，但一方面SVM的核函数选择比较困难，另一方面基于SVM的目标识别算法需要先对回波信号进行特征提取，会损失数据信息，不利于目标识别率的提高。

随着深度学习理论的出现，卷积神经网络(Convolutional Neural Networks, CNN)由于能够自学习数据深层本质特征[8]，在各个领域具有广泛应用[9-12]，使基于采样数据实现对雷达目标的直接识别成为可能，而生成对抗网络(Generative Adversarial Network, GAN)可以生成逼迈真实数据颁的生成样本[13-16]，将生成样本与无标签样本组成真假样本集，通过生成器与判别器的对抗学习，充分利用无标签数据信息，提高判别器的判别能力。

因此，为解决雷达侦察过程中数据库标签样本不足导致目标识别率难以提高的问题，本文将GAN应用于低分辨雷达目标识别领域，并引入CNN作为分类器，提出了基于GAN的半监督低分辨雷达目标识别算法。

1 低分辨雷达目标回波建模

现代雷达辐射源信号常采用线性调频(Linear Frequency Modulation, LFM)信号，使用脉冲压缩技术可使雷达具有很高的径向分辨力，当雷达目标的尺寸大于径向分辨力时，运动目标占据多个距离单元，此时可以使用多散射点模型来模拟目标回波信号。

当雷达发射机发射的是LFM信号时，幅度归一化后可以表示为：

(1)

(2)

(3)

接收机采用变频技术对接收信号进行处理，首先产生一个与发射信号斜率相同的LFM参考信号：

(4)

(5)

(6)

(7)

将变频后的信号输入低通滤波器，对其进行数字采样，获得目标回波采样数据：

(8)

2 基于生成对抗网络的半监督低分辨雷达目标识别算法

2.1 GAN模型

GAN由生成器G和判别器D组成，其中生成器G的作用是根据输入的噪声序列z(通常服从正态分布[10])来尽量产生服从真实数据分布Pdata的生成样本G(z)以欺骗判别器D，而D的作用是判断输入样本是真实样本x还是G(z)，G与D之间相互对抗，互相促进，在不断的对抗中，两者会达到纳什均衡，最终G能够捕获到x的分布并产生能够以假乱真的G(z)，而D则由于无法正确区分x和G(z)，输出逼近一个固定值。GAN的流程如图1所示。

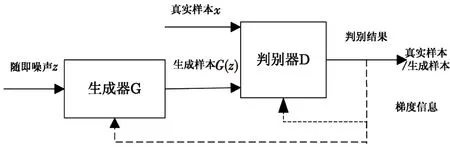
图1 GAN流程图Fig.1 The flow chart of GAN

GAN的目标函数V(D,G)可以表示为：

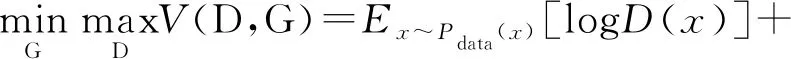
(9)

2.2 基于GAN的半监督识别模型

GAN的判别器D是二分类模型，作用是区分真假样本。在半监督识别算法中，使用CNN替代判别器，输出层连接Softmax分类层，实现分类器的作用，分类器C的输入为标签样本、无标签样本和生成样本，并在K个目标类别外，给无标签样本和生成样本赋予第K+1类真假类别，分类器的作用是当输入标签样本时，输入对应的标签，当输入无标签样本时，在真假类别中输出1，当输入生成样本时，在真假类别中输出0。此时，分类器对三类样本的损失函数如下：

Llabel=-E[logC(x|y)y]

(10)

Lunlabel=-E[log(1-C(x)K+1)]

(11)

Lfake=-E[logC(G(z))K+1]

(12)

式中，Llabel，Lunlabel，Lfake分别是分类器对标签样本、无标签样本和生成样本的损失函数，C(x|y)y表示当输入属于y类的样本x时，分类器C识别为y类的概率；C(x)K+1表示当输入无标签样本x时，分类器识别为K+1类的概率；C(G(z))K+1表示当输入的是生成器产生的生成样本G(z)时，分类器识别为K+1类的概率。由于分类器使用的是Softmax损失函数，利用Softmax函数的特性，即输入各维减去同一个数，Softmax函数输出结果不变。可以令C(x)→C(x)-C(G(z))K+1，则C(G(z))K+1=0，此时，分类器的类别可以用K维来替代，分类器对三类样本的损失函数调整为：

Llabel=-E[C(x|y)y-LSE(C(x))]

(13)

Lunlabel=-E[LSE(C(x))-softplus(LSE(C(x)))]

(14)

Lfake=E[softplus(LSE(C(G(z))K+1))]

(15)

在分类器的损失函数中引入权重系数w，则分类器的总体损失函数为：

(16)

生成器的损失函数为：

LG=-Lfake

(17)

则基于GAN的半监督识别模型的目标函数V(C,G)可以表示为：

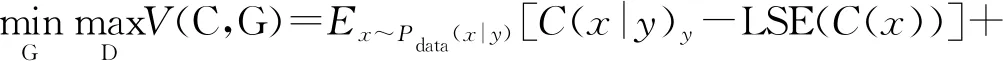
(18)

流程如图2所示。

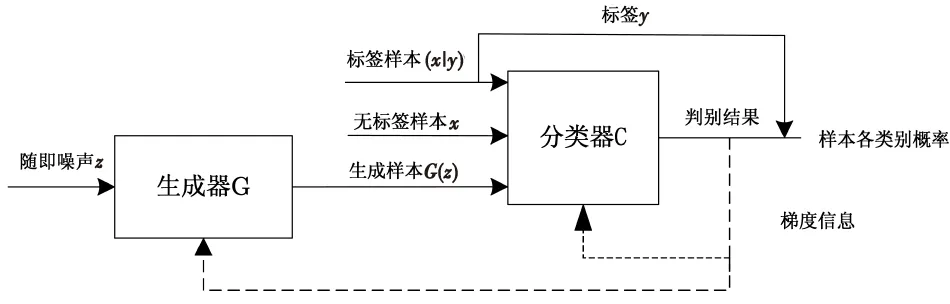
图2 基于GAN的半监督识别模型流程图Fig.2 The flow chart of semi-supervised recognition model based on GAN

2.3 基于GAN的半监督低分辨雷达目标识别算法

在基于GAN的半监督低分辨雷达目标识别算法中，生成器产生逼近真实数据分布的生成样本，分类器为区分生成样本和真实样本，需要挖掘无标签数据中深层本质特征，然后通过标签数据的监督学习选取更利于目标分类的特征，最终实现提高分类器识别性能的目的。

将标签样本，无标签样本和生成样本输入GAN中，训练生成器和分类器，然后将训练好的分类器单独取出作为低分辨雷达目标的识别网络，实现对雷达目标的有效识别。识别算法流程图如图3所示。

识别算法实现步骤如下：

1) 从真实数据集中随机采样m个标签样本(x|y)和m个无标签样本x，从正态分布中随机产生m个噪声z作为噪声样本；

2) 将标签样本、噪声样本和无标签样本作为一批训练样本输入GAN来训练生成器和分类器；

3) 按照预先设定的训练批次和迭代次数，循环步骤1)、步骤2)，将GAN训练完毕；

4) 取出GAN的分类器部分，作为低分辨雷达目标识别网络实现对低分辨雷达目标的分类识别。

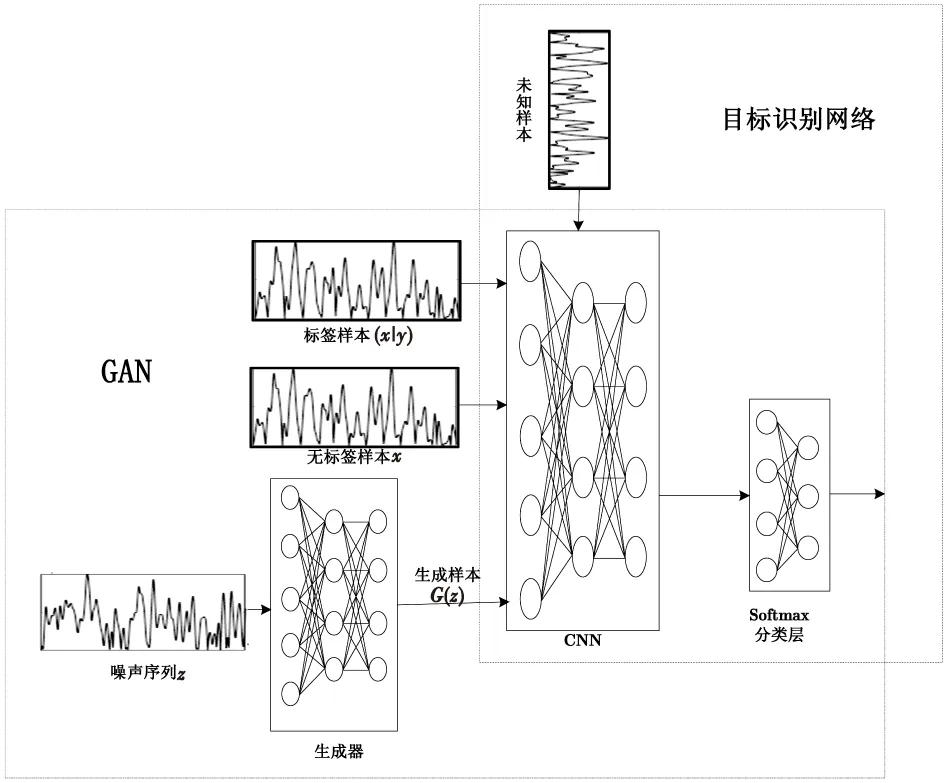
图3 基于GAN的半监督低分辨雷达目标识别算法Fig.3 The semi-supervised low-resolution radar target recognition algorithm based on GAN

3 实验结果与分析

3.1 实验数据集

实验数据集由仿真软件Matlab生成，仿真参数设置：LFM信号载频为3 GHz，调频周期为0.1 ms，调频带宽为100 MHz，采样频率为5 MHz。数值仿真实验对3类目标进行目标识别，分别为人，摩托车和卡车。人的速度是0～6 km/h，摩托车是0～40 km/h，卡车是0～80 km/h，取1个调频周期内的采样数据作为1个样本，通过计算可知样本大小为1×500维，并对通过低通滤波器的采样数据进行幅度归一化和取绝对值处理。在训练样本集中，每个目标类型产生480个标签样本和960个无标签样本，共4 320个样本；测试样本集中每个目标类型产生400个样本，共1 200个样本，其中训练样本集与测试样本集分别独立产生。实验中采用Adam优化器，学习率为0.000 5，动量为0.5，每个批次24个样本，生成器的输入噪声序列服从正态分布。

3.2 网络模型设计

由于实验设备限制，实验中未使用GPU，设计的GAN网络中生成器使用最简单的全连接层，采用三层全连接层，网络模型结构如图4(a)所示，将N×100维的噪声作为生成器的输入，通过两层全连接层后维度转换成N×500的生成样本，其中前两层全连接层先连接归一化层，对全连接的结果做归一化处理后，再进行非线性运算。前两层的激活函数是Softplus函数，第三层的激活函数是Sigmoid函数。分类器采用一维CNN结构，共包含3个卷积层、3个池化层、1个全连接层及Softmax分类器。各卷积层分别包含6个1×13的卷积核，12个1×11的卷积核和30个1×5的卷积核；各池化层分别采用1×4，1×4及1×2的小窗口对卷积后的特征进行不重叠的下采样；Softmax分类器输出1×3的目标识别概率向量。网络模型结构如图4(b)所示。

图4 生成对抗网络结构Fig.4 The structure of GAN

3.3 分类器损失函数参数选择

分类器的损失函数由两部分组成，包括标签样本的分类误差以及无标签样本和生成样本的真假判别误差，其中真假判别误差对分类器损失函数的影响通过权值系数w调节。

由于分类器的主要作用是分类，且无标签样本数往往多于标签样本数。为了防止分类器过多的关注真假判别问题，影响对目标的识别，权值系数w通常远小于1。

为了更好地识别雷达目标，针对不同的权值系数w，进行识别实验。采用信噪比为-6 dB的仿真目标回波采样数据作为网络输入，进行100次蒙特卡洛实验。不同w值下，三种方法的平均识别率如表1所示。其中，当w等于0时，基于GAN的半监督识别算法退化为基于CNN的识别算法。

表1 不同w下的平均识别率Tab.1 Average recognition rate with different w

从表1可以看出，随着w增加，识别率呈现先增加后减少的趋势；当w等于0.01时，平均识别率较高，所以本文算法中选取w=0.01作为权值系数。

3.4 基于GAN的半监督识别模型生成样本

采用信噪比为-2 dB的仿真目标回波采样数据作为网络输入，权重系数w为0.01，训练迭代次数与损失函数的变化如图5所示。图5(a)，(b)分别是分类器判别标签样本和无标签样本的损失函数随训练次数增加而变化的情况。图5(c)表示生成器的损失函数变化情况。

图5 损失函数随训练次数变化图Fig.5 Loss function changes with training frequency

从图5可以看出，分类器前期无法正确区分各类样本，生成器由于逐渐学习到真实样本的特征，损失函数在初期有略微下降现象，后期分类器逐渐学习到真实样本特征并通过监督学习实现对不同样本的有效识别。生成器和分类器在训练过程中相互对抗，在图中呈现出大幅度的震荡，生成器在训练过程中逐渐学习到真实样本的特征，生成样本分布也逐渐逼近真实样本分布，但在总体趋势上，生成器的损失函数逐渐上升，表明分类器的识别能力强于生成器的生成能力，生成器生成能力的增强促使分类器的识别能力的进一步提高。较单纯依靠标签样本训练的CNN，基于GAN的半监督识别方法的识别能力更强。

当输入同一噪声序列时，生成样本随迭代次数Epoch增加产生的变化如图6所示。可以看出，随着训练的加深，生成样本从无意义的噪声逐渐蕴含真实样本特征，且毛刺也在逐渐减少，分布上也越来越逼近真实样本分布，促使分类器挖掘数据中更深层本质特征以区分真假样本。

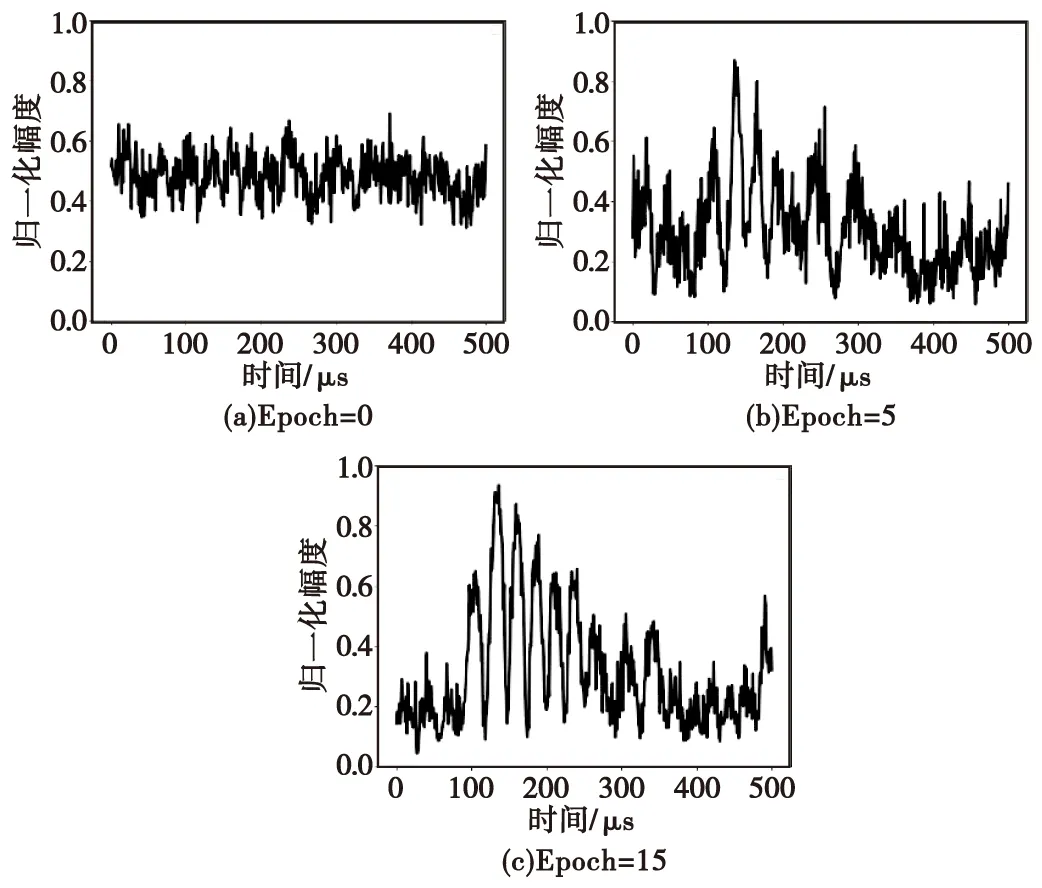
图6 相同噪声在不同迭代次数下产生的生成样本Fig.6 Samples generated by the same noise in different iterations

3.5 基于GAN的半监督低分辨雷达目标识别算法的识别效果

3.5.1 对三类目标的识别效果

为了验证基于GAN的半监督低分辨雷达目标识别算法的可行性，采用信噪比为-2 dB的仿真目标回波采样数据作为网络输入，权重系数w为0.01，进行人、摩托车和卡车三类目标的识别实验。表2是三类目标的识别混淆矩阵，混淆矩阵中每一列表示目标所属的真实类别，每一行表示一维CNN的识别结果。

从表2可以看出，虽然三类目标的识别效果有差异，但识别效果最差的摩托车在信噪比为-2 dB时，识别率仍达到了95.5%，说明基于GAN的半监督低分辨雷达目标识别方法能够有效地对人、摩托车和卡车进行识别。

表2 三类目标识别混淆矩阵Tab.2 Recognition confusion matrix of three kinds of target

3.5.2 样本数对识别效果的影响

为验证本文方法在不同样本数下的识别性能，采用信噪比为-2 dB的仿真目标回波采样数据作为网络输入，权重系数w为0.01，将本文方法与基于CNN的识别方法和文献[6—7]中基于TSVM-MKL算法的识别方法进行比较。

3.5.2.1 无标签样本数对识别效果的影响

实验中标签样本数为120，由于侦察过程中会接收到大量无标签样本，实验中无标签样本与标签样本分别采取(1∶2),(1∶1),(2∶1),(3∶1)和(5∶1)的比例形成训练数据集。通过100次蒙特卡洛实验，三种方法的平均识别率如表3所示，其中基于CNN的识别方法由于不使用无标签样本，识别率不变。

表3 不同比例下各方法的识别率Tab.3 The recognition rate of each method with different proportion

从表3可以看出，本文算法的识别率随着无标签样本比例的增大，呈现先增长后降低的现象，这是由于权值系数w是固定的，随着无标签样本数增多，其对分类器识别性能的影响也就增大，太多的无标签样本反而会影响分类器的识别性能；且无标签样本数越多，网络的训练时间越长。综合考虑，无标签样本与标签样本按照2∶1的比例形成训练数据集能够较好的训练识别网络。

3.5.2.2 标签样本数对识别效果的影响

实验中标签样本数分别为120,240,480,960和1 920，无标签样本与标签样本采取2∶1的比例形成训练数据集。通过100次蒙特卡洛实验，三种方法的平均识别率如表4所示。

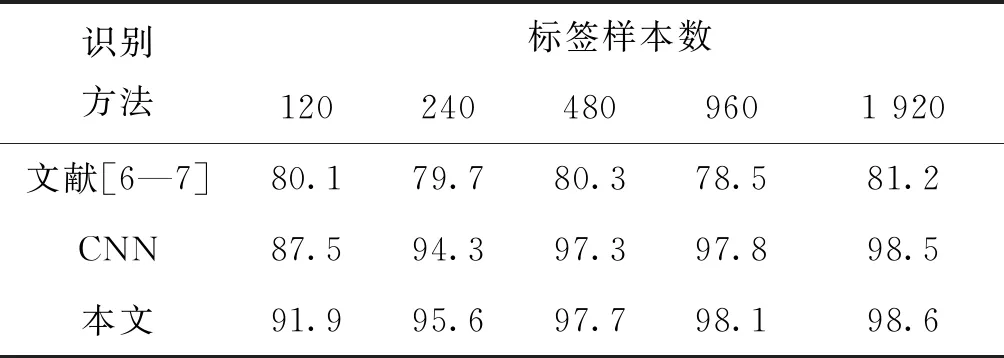
表4 不同标签样本数下各方法的识别率Tab.4 The recognition rate of each method with different labeled sample sizes

从表4可以看出，文献[6—7]算法识别效果受标签样本数影响较小，识别率维持在80%左右，而本文算法和基于CNN的识别方法受标签样本数影响较大。但当标签样本数为120时，本文算法识别率仍达到了91.9%，较文献[6—7]方法提高了11.8%，较基于CNN的识别方法提高了4.4%，进一步证明了本文算法的有效性。

3.5.3 信噪比对识别效果的影响

为验证本文方法在不同信噪比下的识别性能，将本文方法与基于CNN的识别方法和文献[6—7]的识别方法进行比较。用添加高斯白噪声的方法对数据进行加噪处理，信噪比分别是-10 dB，-8 dB，-6 dB,-4 dB和-2 dB。通过100次蒙特卡洛实验，三种方法的平均识别率如图7所示。

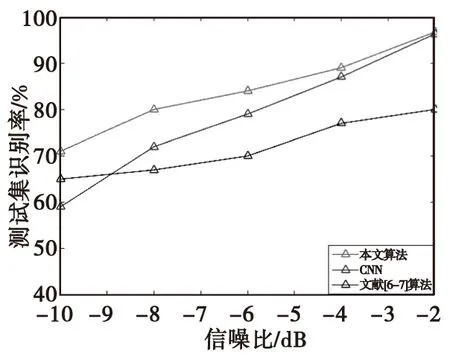
图7 3种方法在不同信噪比下的平均识别率Fig.7 The average recognition rates of thethree methods at different SNR

从图7可以看出， 采用CNN的识别方法由于是基于采样数据的直接识别，保留了数据全部信息，当信噪比较大时，现有标签样本能够较好的训练CNN，识别率明显高于文献[6—7]算法，而当信噪比为-10 dB时，噪声较大，基于CNN的识别方法通过现有标签样本较难学习数据深层特征，识别率低于文献[6—7]算法。而本文所提基于GAN的半监督低分辨雷达目标识别算法，在利用CNN实现对采样数据直接识别的同时，利用了大量无标签样本，挖掘了数据更深层本质特征，识别效果明显优于基于CNN的识别方法和文献[6—7]算法。

3.5.4 算法识别时间对比实验

对文献[6—7]算法和本文算法的识别时间进行计算，结果如表5所示。可以看出，本文算法由于在识别过程中无需对信号进行特征提取，识别时间远远少于文献[6—7]算法的识别时间。

表5 两种算法的识别时间Tab.5 The recognition time of the two algorithms

4 结论

本文提出了基于GAN的半监督低分辨雷达目标识别算法。该算法将GAN应用于低分辨雷达目标识别领域，用CNN替代判别器实现多分类功能，将生成样本和无标签样本形成真假类别属性，利用GAN的对抗生成特点，提高分类器的识别能力，然后将分类器取出作为低分辨雷达目标识别网络。仿真实验结果表明，本文所提的基于GAN的半监督低分辨雷达目标识别算法较传统半监督低分辨雷达目标识别方法在识别准确度和运算速度上都有明显优势。