基于稀疏系统辨识的收发隔离方法

郝治理，刘春生，周青松

(国防科技大学电子对抗学院，安徽 合肥 230037)

0 引言

对于无人机等小型平台上的雷达干扰机，接收天线与发射天线之间的距离较近，当干扰机发射干扰信号时,会有一部分干扰信号耦合到接收端。如果到达接收机的干扰信号大于接收机的灵敏度则会影响侦察接收机的正常工作，严重时会发生收发自激。影响收发隔离的主要因素有[1]：1) 干扰发射天线和侦察天线的副瓣作用；2) 由于天线罩的反射，自身的绕射以及周围近距离散射体的反射，会引起多径信号进入接收机。通常情况下这些路径具有小延时、时不变的特性。传统意义上主要通过两种方式来解决干扰机的收发隔离问题：一是降低侦察接收机灵敏度，二是侦察与干扰分时工作[2-3]。但是第一种方式会降低对弱信号的检测概率，第二种方式不能实现收发同时工作，既降低了侦察效率，也影响了干扰效能。

当前，系统辨识成为了解决收发隔离问题的主要手段。早在20世纪70年代，哈佛大学教授Kashyap等人就已经开始了对系统辨识的研究。经过几十年发展，通过对未知系统采用自适应滤波器建模，成功地将最小二乘(Least Squares，LS)法、梯度校正法、极大似然法和自适应最小均方(Least mean Square，LMS)算法等应用于线性系统辨识问题[4-5]。系统辨识是指在输入和输出数据的基础上，从给定的一组模型中，确定一个与所辨识系统等价的模型[6]。利用这个思想，可以把雷达干扰机外界耦合环境看作一个未知系统，利用系统辨识方法估计出其传递函数，进而根据己方发射的干扰信号和系统传递函数估计出耦合干扰信号，最后在接收端完成干扰对消，从而实现收发隔离。然而在现实环境中很多系统都具有稀疏性质，即系统的冲激响应在时间域上只有少量的非零值，比如水声通信信道、回声路径等[7]。实际上，耦合干扰信号可以看作是干扰信号经过不同的耦合路径即不同的延时在接收端的叠加。若指定一个延时单位，由于耦合路径是有限的，在包含最大延时的范围内，并不是每隔一个延时单位都会存在干扰信号的耦合，因此可以将耦合路径看作是稀疏存在的。此时，常用的LS算法虽能够对数据实现较好的拟合[8]，但由于系统噪声的存在，会在真实衰减系数为零的路径处引起较大的估计误差，从而会降低隔离性能。针对此问题,参考零吸引(Zero-Attracting)LMS算法和重加权零吸引(Reweighted ZerovAttracting)LMS算法[9-10]，在LS算法代价函数的基础上引入了待估计系数矢量的l1范数约束，提出了l1-LS和l1-OMP(Orthogonal-Matching-Pursuit)算法。这两种算法增加了估计路径系数的稀疏倾向性[11]，提高了路径系数的辨识精度，进而能够提高收发隔离度。

1 基于LS估计的收发隔离方法

1.1 模型建立

系统辨识用于解决收发隔离问题的实质是将干扰机的干扰信号耦合路径等效为一个符合特定模型的系统。通过发射探测信号对外界系统进行冲激，根据已知的发射信号和接收信号，利用相应的辨识算法对系统的传递函数进行辨识。一旦将系统传递函数辨识出来，就可以在干扰机工作的同时，根据发射信号和系统传递函数估计出耦合到接收端的干扰信号，将此部分信号在接收端对消掉，即实现了收发隔离。基于系统辨识的收发隔离模型如图1所示[12]。

图1 收发隔离模型Fig.1 Transceiver isolation model

d(n)=s(n)+y(n)

(1)

(2)

1.2 LS算法

在线性情况下通常利用FIR滤波器来代替图1中的辨识通路。而辨识通路结构与干扰信号耦合路径基本一致，将滤波器系数看作是耦合路径的衰减系数，即本文需要辨识的参数，构建FIR滤波器模型如图2所示。

干扰机发射的干扰信号x(n)经过图2所模拟的耦合路径到达接收端的过程可以表示为：

(3)

式(3)中，M为假设待辨识路径个数，滤波器系数由wi(n)(i=1,2,…,M)表示，v(n)表示系统噪声。本文假设在稀疏时不变的环境下，因此存在部分wi(n)=0。为了对图2系统进行辨识，需要利用探测信号对系统进行冲激，在本文余下部分x(n)为探测信号。令n=1,2,…,N，进一步将式(3)表示成矩阵形式：

(4)

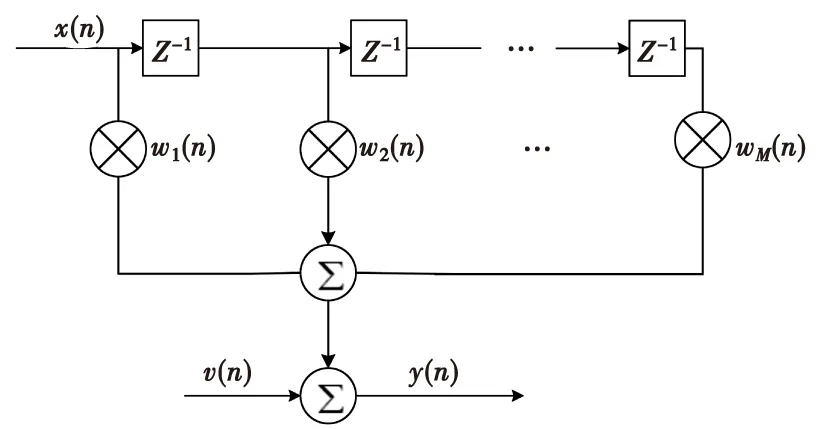
图2 FIR滤波器模型Fig.2 FIR filter model

我们期望利用探测信号构成的矩阵Z和接收信号y求解出滤波器系数w，即求解目标函数：

(5)

对式(5)进行求导，并令其导数值为零：

(6)

可以得到滤波器系数w为：

(7)

到这里已完成了系统辨识，之后当雷达干扰机发射干扰信号时，结合式(2)和式(4)便可以实现收发隔离。但是在本文的稀疏环境下，真实存在的耦合路径个数k远小于滤波器长度M，LS算法会产生较大的信道估计误差[13]，进而会降低隔离效果。

2 基于稀疏约束的收发隔离方法

2.1 l1-LS算法

针对LS算法无法精确估计稀疏路径的衰减系数，本小节提出一种新的算法。该算法的核心思想是挑选出衰减系数不为零的耦合路径所对应的列向量Xk以及滤波器系数wk(k≤M)，并将它们重新放入到新的字典和滤波器矢量组合中，然后利用重新组成的字典和滤波器系数向量对y做最小二乘。算法的求解步骤如下：

首先，在LS算法的代价函数中增加关于w的稀疏约束，通常选择增加‖w‖p，p的取值在[0,1]之间。其中0范数是最能体现稀疏性的代表，但是基于其求解的复杂性，我们最终选择增加w的1范数[14]，即：

(8)

式(8)中，λ是正则化系数，可以用来控制代价函数中拟合误差与稀疏倾向的平衡与折中。利用现有的凸优化方法求解目标函数(8)非常简单，对其进行求解可以使w中接近0的系数更加趋近于0。然后选取参数ξ，ξ的取值略大于系统噪声幅度与探测信号幅度的比值，令w中所有小于ξ的系数为零。

(9)

即认为如果y中某一位置信号强度与系统噪声相当，则此部分接收信号是由噪声作用，而与探测信号无关。

然后根据现有的w，将字典矩阵X中与非零滤波器系数对应的列挑选出来，组成新的字典矩阵，最后仅根据挑选出的列再进行最小二乘，即求解

(10)

式(10)中，wk表示根据上一步中非零系数重新组成的滤波器矢量，而Xk表示由上一步挑选出的列组成的新的字典矩阵，对上式进行求解可得：

(11)

将上式求解的滤波器向量根据前面抽取的位置，重新放入其原位置，这样就完成了对主要耦合路径所对应的滤波器系数的精确求解，而在其余位置对应系数全为0，保证了干扰耦合路径的稀疏性。

需要注意的是，l1-LS算法在第一步求解过程中更加注重的是稀疏性，即所求解的w对接收数据的拟合效果比较差，仅仅是为了剔除逼近0的滤波器系数提供依据。直到第二步才真正对前面挑选出的路径所对应的滤波器系数进行精确求解。l1-LS算法适用于探测信噪比较高的环境下，如果探测信噪比下降，该算法在挑选稀疏存在的耦合路径时，难以剔除噪声的影响，挑选出的路径数往往会大于真实的路径数，即对主要路径的提取结果会比较差。

2.2 l1-OMP算法

当探测信号功率较小，且噪声功率较大，即探测信噪比较低时，本小节采用OMP方法对l1约束下挑选出的路径进行二次筛选，具体实施过程如下：

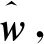
然后，利用OMP算法进行二次挑选，近似求解P0问题：

(12)

每次使l加1，并执行以下步骤：

步骤1 对所有的j，计算优化的参数选择：

(13)

并计算误差：

(14)

步骤2 更新支撑集确定使ε(j)取最小值的点j0，∀j∉Sl-1，ε(j0)≤ε(j) ，并更新支撑集Sl=Sl-1∪{j0}；

(15)

综上，该方法首先利用了l1范数的稀疏倾向性，对干扰耦合路径进行了初步提取，然后再利用OMP算法对初步提取的结果进行二次筛选，这与直接使用OMP算法相比大大降低了计算复杂度。

3 仿真实验

3.1 性能评价指标

为了便于分析算法的优劣性，在进行仿真实验之前，首先介绍一下常用于判断干扰机收发隔离性能的指标。主要包括：隔离度、隔离后信干比和信道估计误差。

1) 隔离度(I)：

(16)

式(16)中，pt表示雷达干扰机发射的干扰信号功率，pr表示经过隔离以后的残余干扰信号功率，可以看出隔离度I反应了发射干扰信号相对于残余干扰信号的大小，当发射干扰信号功率一定时，隔离度越高说明经过隔离的残余干扰信号功率越小，即隔离效果越好。

2) 隔离后信干比(SJR)：

SJR=10lgps/pr

(17)

式(17)中，ps表示隔离之后雷达信号的功率，pr表示经过隔离之后的干扰信号的功率。可以看出隔离后信干比越大表示隔离性能越好。

3) 信道估计误差(SD)：

(18)

式(18)中，w0表示真实的FIR滤波器系数，w表示经系统辨识方法估计出的滤波器系数，信道估计误差值越接近于零，表示对路径系数的辨识越精确，最后的隔离效果就会越好。

3.2 高探测信噪比下的实验分析

测试在高信噪比环境下三种算法的隔离性能。仿真环境和参数设置如下：设定系统噪声是均值为0，标准差为0.01的白噪声，探测信号与系统噪声的功率比取40 dB。设干扰机侦察接收机的接收频率范围为[0 MHz,500 MHz]。理论上应该选择伪随机噪声作为探测信号更容易获得系统的冲激响应，但实际中无法产生纯净的伪随机噪声。而文献[8]指出探测信号x(n)的选择应该使XTX为对角阵，除了伪随机噪声以外，宽带线性调频信号刚好能近似满足这一条件，因此这里选择带宽为400 MHz，频率变化范围为[50 MHz,450 MHz]的宽带线性调频信号作为系统辨识探测信号。信号的脉冲宽度设为2 μs，采样时间与信号脉冲宽度相同，采样频率设置为1 GHz。

假设侦察接收机正在接收的雷达信号是中心频率200 MHz，带宽50 MHz的线性调频信号。假设雷达干扰机是针对于该信号施放基于DRFM的移频干扰信号，移频量设为1 MHz，假目标数设为4，且干扰信号的频率范围设为[175 MHz，225 MHz]。设干扰信号与系统噪声的功率比为40 dB，因此隔离度达到40 dB时，才能实现干扰机的收发同时工作。

假设滤波器阶数为30，设待辨识的路径系数为w0=[0.9,0,0.7,0,0.5,0,…,0.3,…,0]，只有在1,3,5,27位置上存在干扰信号耦合现象。虽然系统辨识要控制对数据的拟合误差在一定范围内，但是本文所提出的两种算法第一步重点考虑路径的稀疏性，故正则化系数λ的取值应该略大于拟合误差前置系数，在此取1。在本文的应用环境中，ξ和ζ取值为0.03。进行50次Monte-Carlo模拟仿真实验，并对所得结果进行分析，判断本文所提出的两种方法用于雷达干扰机收发隔离的实际效果。

如图3所示，干扰机接收端同时收到混合信号与雷达信号。可以看出，此时耦合干扰信号已经完全覆盖住了雷达信号，这将导致雷达无法正常识别有用信号，会影响其侦察工作，无法实时检测外界雷达信号，也会对之后干扰机的干扰工作造成一定的影响。

图3 接收混合信号与雷达信号Fig.3 Receiving mixed signals with radar signals

图4显示了经过本文两种算法隔离之后的信号与雷达信号，其中图4(a)是l1-LS算法的隔离效果，图4(b)表示l1-OMP算法的隔离效果。容易看出经过这两种算法隔离后的信号与干扰机接收的雷达信号基本吻合，即两种算法均成功地隔离了影响接收机工作的耦合干扰信号。

图4 隔离后信号与雷达信号Fig.4 Isolated signal and radar signal

图5从干扰信号的角度更直观地显示了l1-LS和l1-OMP算法对耦合干扰信号的隔离程度，通过对比可以看出经过本文两种算法隔离后残余干扰信号不过在-40 dB左右，即耦合干扰信号基本被隔离掉。

图5 耦合干扰信号和残余干扰信号Fig.5 Coupling interference signal and residual interference signal

为了进一步分析本文算法的隔离性能，下面根据3.1节介绍的隔离性能指标对比本文两种算法与LS算法的优劣性。

图6分别显示了三种算法的信道估计误差，图6(a)、(b)分别对LS算法与l1-LS和l1-OMP算法的信道估计误差进行了对比，容易看出LS算法的SD要远大于本文两种算法。通过计算均值，可以得到LS算法的SD为-45.6 dB；l1-LS算法的SD为-63.7 dB；l1-OMP算法的SD为-64.7 dB。即本文提出的两种算法在高信噪比条件下辨识精度相当。

图6 信道估计误差Fig.6 Channel estimation error

图7显示了三种算法分别进行50次仿真实验后的信干比变化曲线，隔离前信干比为-2 dB,容易看出经过本文两种算法隔离后的信干比明显优于LS算法隔离后的信干比。

最后，图8显示了伴随50次实验的隔离度变化曲线，分析图7容易得到，在本文的仿真环境下，本文两种算法对消之后的隔离度相对LS算法有了一定的提高，基本达到了40 dB，满足了隔离需求。

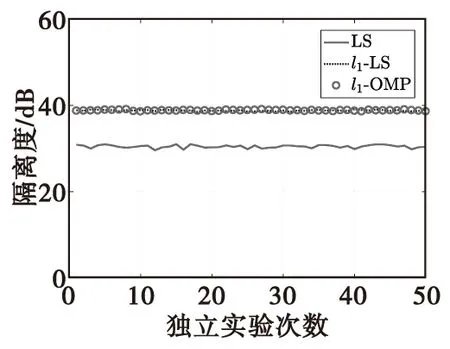
图8 隔离度Fig.8 Isolation

综上所述，在路径稀疏且高探测信噪比的环境下，本文所提出的两种算法均能满足雷达干扰机的隔离需求。并且根据第2节对两种算法的描述，两者第一步所得到的结果是一致的，而OMP算法是一个循环过程，每次循环都要进行LS运算，仅是其最后一次LS运算都与LS算法的复杂度相当，故l1-OMP算法的复杂度要高于l1-LS算法。

3.3 低探测信噪比下的实验分析

验证在低探测信噪比的环境下l1-OMP算法是否还能保持良好的隔离性能。探测信号与系统噪声的功率比取20 dB，仿真环境和参数设置与实验1相同。首先对l1-OMP算法的隔离效果进行分析。

隔离前的频谱图与图3相同，图9表示经过l1-OMP算法隔离后的效果。可以看出，经过该算法隔离以后的信号与所侦察的雷达信号基本吻合，即耦合干扰信号基本被对消掉，并且对于正在侦察的雷达信号没有造成影响。分析图10，残余干扰信号被压制在-40 dB左右,即干扰信号能量基本被对消掉。

图9 隔离后信号与雷达信号Fig.9 Isolated signal and radar signal

为了进一步验证l1-OMP算法在低信噪比条件下的优越性，同样对三种算法的隔离性能进行分析。

图10 耦合干扰信号和残余干扰信号Fig.10 Coupling interference signal and residual interference signal

图11分别显示了三种算法的信道估计误差，从图11(a)、(b)分别对比了LS与l1-LS算法、l1-LS与l1-OMP算法的信道估计误差。经过计算，LS算法的信道估计误差均值为-20.17 dB；l1-LS算法的信道估计误差均值为-43.49 dB；l1-OMP算法的信道估计误差均值为-58.03 dB； 故l1-OMP算法在低信噪比环境下依然保持着较高的辨识精度。

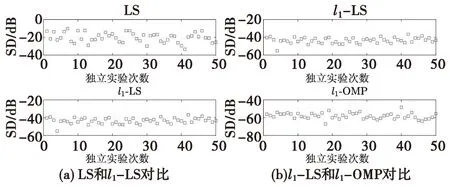
图11 信道估计误差Fig.11 Channel estimation error

图12显示了三种算法隔离后的信干比变化曲线，容易看出经过l1-OMP算法隔离后的信干比最高，而经l1-LS算法隔离后的信干比虽然总体优于LS算法，但相对于高信噪比环境下的性能有所下降。

图12 隔离后信干比Fig.12 Isolation ratio

最后，图13显示了经过三种算法隔离后的隔离度变化曲线，可以得到，在低信噪比的仿真环境下，l1-OMP算法对消之后的隔离度依然很接近40 dB，而l1-LS和LS算法已经无法满足实际隔离需求。

图13 隔离度Fig.13 Isolation

4 结论

本文提出了两种基于稀疏系统辨识的收发隔离方法。这两种方法能够充分利用干扰耦合路径稀疏这一先验信息，在对路径系统进行辨识时首先将主要耦合路径提取出来，然后在此基础上进行精确辨识，提高了稀疏背景下的系统辨识精度。理论分析和仿真实验表明，在稀疏高探测信噪比环境下，l1-LS和l1-OMP算法均能使干扰机达到隔离需求，但是l1-OMP算法的复杂度要高于l1-LS算法。而在低探测信噪比环境下，虽然两种算法的辨识精度依然优于LS算法，但l1-LS算法的辨识精度以及隔离性能均有所下降，而l1-OMP算法仍然可以达到隔离需求，能够实现雷达干扰机的收发同时工作。