一种基于齿科序列图像的超分辨率重建算法

程 斌，汪 伟

(上海理工大学 光电信息与计算机工程学院，上海 200093)

1 引 言

医学影像在临床上应用广泛，能够为疾病的诊断提供科学、直观的依据；同时也能够结合临床的症状、化验等结果，为最终病情的确定和后续的治疗计划提供重要参考.但是，由于物理分辨率的限制，成像的质量远远不能满足医学上的需求.为了获取更高分辨率影像，常采用减小传感器像素尺寸或增大成像阵列芯片大小等硬件的方法.但当像素尺寸减小时，加性噪声几乎维持不变，有效信号的能量将随传感器像素尺寸成比例减小；而后者高精度光学传感器的增大又将会显著增加成本，给医疗设备的普及带来重要阻碍.因此，为了规避硬件发展的瓶颈，许多研究者深入地分析了图像的成像过程，构建出较为理想的图像退化模型，并尝试利用同一场景下获得的低分辨率序列图像，通过软件计算来重构出高分辨率的影像.这一思想得到了快速发展，且很快成为了目前研究的热点问题之一.

当前，基于空域的超分辨率序列图像重建算法不断被提出，包括非均匀插值法、迭代反投影法(iterative back projection,IBP)、凸集投影法(projection onto convex sets,POCS)、最大后验概率法(maximum a posterior，MAP)，POCS-MAP混合法等[1,2].在医学中，Wissam基于两正交的低分辨率核磁共振(magnetic resonance imaging，MRI)数据集和电子计算机断层扫描(computed tomography，CT)数据集，在上采样的插值过程中，利用欧式距离计算出每个像素置信度，并结合区域和局部信息，构造损失因子，修补了IBP算法中的高分辨率图像初始估计[3]；Esben Plenge等人考虑不同的数据和噪声模型，根据MAP法可灵活调整数据保真项(如l1,l2范数)和正则项(如Tikhonov，总变分正则项等)的特点，将IBP、MAP+ Tikhonov正则项、MAP+Lambda权重正则项3种序列图像超分辨率重建(multi-image super resolution reconstruction，MISR)方法计算结果与通过高分辨率硬件成像设备直接获取的MRI图像进行比对分析，发现MISR方法能获得更好的评价结果[4]；Jonghye Woo等结合Markov随机场，提出了一种基于舌头MRI序列图像的重建方法[5]；除此之外，Hayit Greenspan对MISR方法在医学图像MRI，FMRI(functional MRI)，PET(positron emission tomography)上的应用进行了回顾与分析，并以大脑影像为例，比较了不同MISR方法的效果与局限性[6].

除了上述提到的MRI图像外，M.Dirk Robinson等在前人应用的基础上，将MISR扩展到乳房X光片(X-ray digital mammography)和光学相干断层扫描(optical coherence tomography,OCT)应用领域上[7]；Hong等利用光流法配准后，基于IBP方法完成了超声图像的超分辨率重建[8].在2016年，Springer期刊上发表了一篇《智能优化在生物医学中的应用》专刊[9]，详细介绍了超分辨重建算法的发展，重点谈到了最优化方法在医学图像重建上的应用.并结合癌症成像数据库，对采用bicubic插值、IBP、POCS、通过稀疏表示的梯度下降法这四种方法的重建结果进行了分析.

与基于空域的方法相对应，研究者们也提出了基于频域的超分辨率序列图像重建算法.在频域中，成像模型内的卷积、几何运动等操作都将被转换为线性的计算，超分辨率重建问题等效为了线性逆向模型的求解，各种频域变换如离散余弦变换、小波变换、Contourlet变换等在医学上相继得到了应用.Kumar V.R.等人通过对小波变换后子带系数的奇异值估计和插值法重建了大脑CT、胰腺CT和胸部X光片[10]；Yan Shen等基于Contourlet变换重建了乳房X射线图，帮助乳腺癌诊断中的钙化检测[11].在2005年，Arthur L.等提出了非下采样Contourlet变换(the non-subsampled contourlet transform,NSCT)[12]，该方法相对于小波变换、Contourlet变换具有平移不变性的特点.国内的杨贞萍，周靖鸿等人分别则采用该变换，选用光流法配准和矩阵乘法配准，通过系数融合策略重建出文本图像[13]和遥感图像[14]，这也给该变换在医学图像上的应用提供了可能.

近年来，基于学习的超分辨率重建算法[15,16]得到了快速发展，其中单帧图像的超分辨率重建(single-image super-resolution reconstruction,SISR)方法较多，比如Yang的稀疏表示模型、Dong的卷积神经网络SRCNN、Ledig等提出的生成对抗网络SRGAN等[17]，并且有关研究人员都用在了医学图像上[18-20]，而基于学习的MISR方法相对较少，其大多在SISR基础上，在前级输入中加入运动补偿处理，或设计网络中就考虑多帧信息的融合问题，如VSRnet (video super-resolution with convolutional neural networks)[21],VESPCN (video efficient sub-pixel convolution network[22],Dynamic filter generate on network[17]等.

牙科疾病的多样性和个体的差异性给学习类的重建方法带来了重要麻烦，存在针对不同的病患群体和不同的病灶类型，需获取大量的训练样本和实时效率的问题；而在传统的MISR方法中，文献[13]、文献[14]等提出的配准方法又只能处理序列图像间的平移情况；另外口腔图像细节的损失将会严重影响牙医的最终诊断，因此本文提出了一种针对医学齿科序列图像的超分辨率重建算法.该算法创新性地将点云中的配准方法，即迭代最近邻点法[23,24](iterative closest point，ICP)引入到齿科序列图像的超分辨率重建过程中，并分别在配准点集筛选和配准策略上进行了改进，增强了算法的鲁棒性与精确度，从而可以克服实际检测过程中口腔内部组织三维运动所带来的配准难题；其次，算法中采用基于多尺度的NSCT变换来融合齿科序列图像的有效信息，NSCT变换具有平移不变性的特点，其非下采样的过程不但可以弥补图像分解过程中信息的丢失，使边缘等细节特征得以保留，而且通过对子带系数的处理，可以将噪声信息从图像信息中有效滤除，从而改善超分辨率齿科图像的重建结果，更好地辅助牙医诊断病情和制定治疗计划.

2 基于齿科序列图像的超分辨率重建

2.1 图像退化模型

图像的退化过程是超分辨率重建算法得以实现的理论基础和依据.现常用的图像退化(观测)模型如图1所示.

图1 图像退化模型[1]Fig.1 Image observation model

上述模型数学表达为：

yk=DBkMkx+nk(1≤k≤p)

(1)

其中x表示高分辨率图像HR；yk表示第k张低分辨率图像LR；Mk表示几何形变矩阵；Bk对应着模糊矩阵，如传感器、运动、光学等模糊，常被模型化成各种点扩散函数(a point spread function, PSF)；D代表下采样矩阵；nk、p分别表示加性噪声和低分辨率序列图像帧数.

超分辨率算法的重建过程，即是图像退化模型的逆过程.因此，要实现高分辨率图像的重建，必须完成如下三个步骤：矫正低分辨率序列图像之间的几何运动、去除模糊和噪声、图像上采样处理，这也构成了本文算法的理论基础.

2.2 齿科序列图像超分辨率重建算法流程

如图2所示，齿科序列图像超分辨率重建步骤可简述如下：

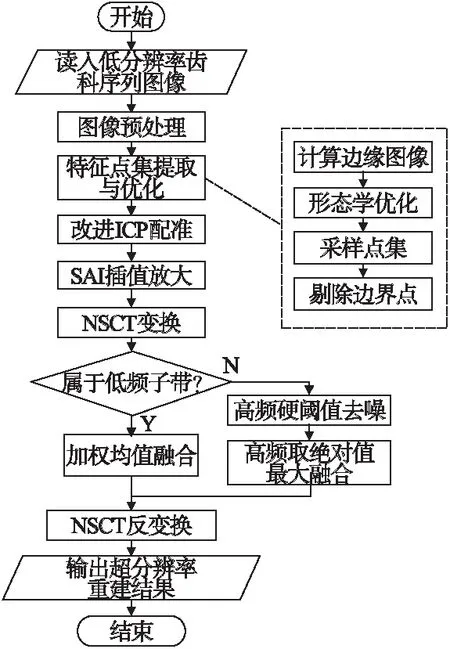
图2 本文重建算法主流程Fig.2 Main flow chart of the proposed reconstruction algorithm

1)读入从口腔诊疗设备获得的低分辨率齿科序列图像，并进行预处理；

2)结合梯度算子计算边缘图像，形态学优化后，提取出初步特征点集，然后经过采样和边界点剔除，形成优化后的配准点集，如图2中虚线框部分所示；

3)设定鲁棒损失函数，进行ICP算法的迭代配准过程，求得最优几何变换矩阵，并对序列齿科图像进行矫正；

4)利用软判决自适应插值法，插值放大已配准的低分辨率序列图像；

5)采用NSCT变换，提取各图像的低频子带和高频子带，对低频子带系数采用加权均值融合的策略，对高频子带系数用硬阈值去噪后，采用取最大绝对值的融合策略；

6)将NSCT各个子带系数完成融合后，再结合NSCT反变换，得到最后的超分辨率重建齿科图像.

2.3 图像的预处理

为改善口腔视频图像存在的噪声干扰及光照不均匀现象，首先需对源图像进行预处理，即图像直方图均衡化：

(2)

式(2)中rk代表归一化后的离散灰度级，且0≤rk≤1,k=0,1,2,…,n-1；ni为图像中第i个灰度级的像素数；n为图像中的像素总数.

2.4 图像的配准

在序列图像的超分辨率重建方法中，最基本的思想就是整合捕捉到的多帧低分辨率图像信息来提高空间分辨率，而信息整合的好坏，很大程度上取决于图像配准的精度.

本文采用迭代最近邻点法配准低分辨率序列图像，矫正序列图像间存在的几何运动.经典ICP配准方法最早由Besl和McKay提出[23]，并在点云的配准上得到了广泛应用.但该方法对异常点对不敏感、干扰点的存在会引起配准效果的急剧恶化、点集之间需满足包含的关系，而超分辨率重建结果严重依赖于配准效果.所以，本文创新性地在点集的筛选和配准策略上改进了ICP算法，以提高低分辨率齿科序列图像间运动估计的精度.

2.4.1 配准点集提取与优化

通过对多种已有特征点提取方法的比较与分析，本文利用预处理图像中的梯度信息和边缘信息，提取出牙体硬组织的边缘特征点作为初始配准点集.

1)牙体硬组织边缘图像LRE的计算

在常用边缘检测算法中，相比于Canny算子,Sobel算子虽然检测精度较低，但具有较低的运算复杂度、对噪声不敏感.故本文采用Sobel算子提取低分辨率图像LR的边缘图像:

LRE=Sobel(LR)

(3)

2)边缘图像的优化

对所获得的边缘图像采用数学形态学中的膨胀操作，既提高了配准点集中有效点的数量，又减少了干扰点在点集中所占的比例，可有效提高配准的精度.

(4)

(5)

3)初始配准点集采样

为了降低计算量，利用采样函数对初始特征点集E进行采样：

Model=sample(ER)

(6)

Data=sample(ETi)(i=2,3,…,M)

(7)

式(6)和式(7)中，ER表示参考帧的初始配准点集，ETi为序列中第i待配准帧的初始配准点集,M为低分辨率医学序列图像帧数，sample()为预设的采样函数，一般可选为均匀采样或者随机采样函数.

4)配准点集的优化

在低分辨率序列图像间的几何运动，造成图像的四周边界处差异最大，而从这些边界处提取出的配准点集间很少存在包含关系，即会对配准迭代的过程产生不利影响.因此，需要去除图像边界处的边缘点，从而优化配准点集：

Model′=Model(|x-xmid|≤T1,|y-ymid|≤T2)

(8)

Data′=Data(|x-xmid|≤T3,|y-ymid|≤T4)

(9)

其中，T1，T2，T3，T4分别为设定的参考帧点集与待配准帧点集坐标变化阈值，xmid、ymid分别为图像中心像素的横坐标与纵坐标.

2.4.2 ICP算法迭代

基于低分辨率参考帧和待配准帧完成特征点集提取和优化后，得到优化点集Model′和Data′.在经典的ICP配准策略中，所有最近邻点对的权重都是相同的；但是，对于匹配点间欧式距离过大的情况，极大概率是属于异常干扰点.因此，为增加配准过程的鲁棒性，引入鲁棒损失函数来调整不同匹配点对所对应的权值，从而减少异常匹配点对的干扰.其改进后的ICP算法迭代步骤可简要描述为：

1)设置鲁棒损失函数.常见的鲁棒损失函数[25]及对应的权值函数如下：

-Huber函数

(10)

(11)

-Tukey′s Biweigh函数

(12)

(13)

-Cauchy函数

(14)

(15)

其中r指的是残差，kHu、kTu和kCa为预设值.

2)输入低分辨率参考帧点集Model′和待配准帧点集Data′，根据鲁棒损失函数调用相应的权值函数，并设置初始旋转矩阵和平移向量为单位矩阵E和零向量；

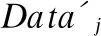
4)以配对点对之间的欧式距离为依据，结合权值函数，确定所有配准点对的权值ωj；

5)根据上述权值大于0的配对点，求得使目标函数Dmin最小化的刚体变换，得出平移参数和旋转量；

(16)

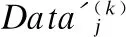
(17)

其中R(k)，T(k)分别为迭代计算的旋转矩阵和平移向量.

6)如果变换点集与源点集之间的均方根误差RMSE小于某一给定阈值,或达到设定的最大配准迭代次数时，停止迭代计算；否则，将变换后的点集作为新的待配准点集，按照步骤3)至步骤5)继续与源点集迭代计算，求取最优的变换参数.

其完整的配准迭代过程伪代码[25]如下：

算法.The Modified ICP algorithm

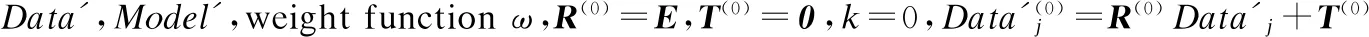
输出:R(k),T(k)

1.Repeat

2.k=k+1

5. if anyωj>0 then

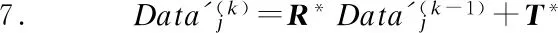
8.R(k)=R*R(k-1)

9.T(k)=R*T(k-1)+T*

10. else

12.R(k)=R(k-1)

13.T(k)=T(k-1)

14. Terminate iteration

15. end if

16. until convergence

17.ReturnR(k),T(k)

2.5 软判决自适应插值放大

在改进ICP配准法完成齿科序列图像的帧间配准后，本文选用在保持图像空间一致性上有优异表现的软判决自适应插值法(soft-decision adaptive interpolation，SAI)[26]提高图像空间分辨率，有效降低插值后的模糊、振铃和锯齿现象.

如图3所示，黑点代表已知的低分辨率像素点，白点和灰点表示待插值的高分辨率像素点.SAI插值算法将先建立图像的分段自回归过程(PAR)模型，其中模型参数分别由图3(b)中八邻域像素值、图3(c)中四邻域像素值得出.然后，基于指定滑窗中的最小均方误差估计出图3(a)中灰点的像素值；最后，将模型旋转45°，估计出白点的像素值，从而得到完整放大后的高分辨率图像.

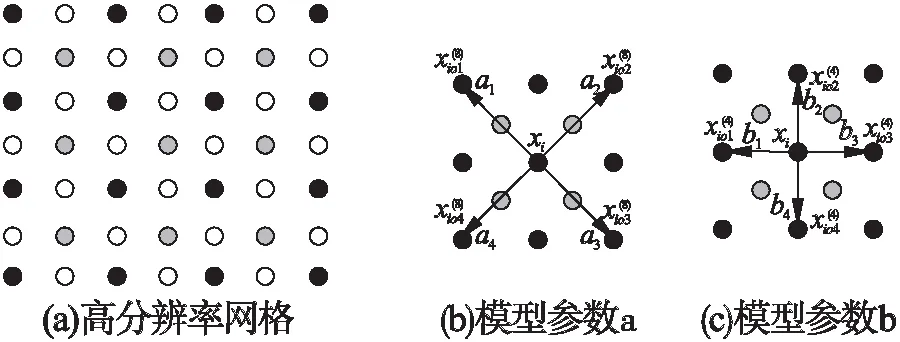
图3 SAI插值法Fig.3 Soft-decision adaptive interpolation

因此，对已配准的低分辨率齿科序列图像采用SAI插值法放大factor倍，其计算公式可表示为：

(18)

2.6 NSCT域图像融合

插值放大后的低分辨率序列图像像素增加，但图像间的信息仍然独立，需结合NSCT变换[12]实现齿科序列图像信息的有效融合.相对于Contourlet变换，NSCT去掉了金字塔分解和方向滤波器分解中的下采样及综合滤波前的插值过程，而改为对滤波器进行上采样、再对信号进行分析滤波和综合滤波，有效减少了信息的丢失.其融合过程可表述为：

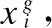
(19)

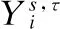
(20)

2)HRi序列图像经过NSCT变换分解后，本文采用的融合策略为：低频采用加权均值的融合方法，主要由于超分辨率重建的重点是重建参考帧，所以会改变参考帧在均值融合过程中所占的比例；高频采用比较经典的取绝对值最大的融合方法，同时为有效减少图像噪声，会在高频融合前，进行一次硬阈值去噪，即去噪阈值设为对应子带系数的均方差倍比.

NSCT变换后低频系数的融合：

(21)

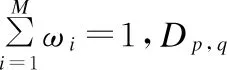
NSCT变换后高频系数的融合：

(22)

(23)

(24)

(25)

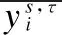
3)融合后便可得到优化的低频分量和高频分量，低分辨率齿科序列图像间的信息进行了整合与互补，采用NSCT反变换，得到最后的超分辨率齿科重建图像HR.

(26)

其中c-1为NSCT反变换算子.

3 实验结果

3.1 建立图像数据库

本文所采用图像数据库均来源于通过口腔诊疗设备采集的齿科视频文件，共截取20,000余帧，分辨率皆为640*480.按照实验的要求，从中选取200帧较为清晰的图片作为超分辨率重建结果的参考图像.根据这200张图像，会根据图1的图像退化模型模拟生成800张低分辨率图像，即1张高清图像对应于4张低分辨率图像.因退化图像相对于参考图像会存在相对的几何运动，考虑到序列图像间差异度较小，其平移的像素范围预设为[-10,+10]，角度旋转范围为内[-10°,+10°]；除此之外，生成的退化图像中还添加了高斯噪声，其方差范围为(0.0001～0.0005).最终生成的800张退化图像构成了算法测试数据库，其中平移情况占30%，旋转情况占30%，旋转与平移两种情况皆有的例子占40%.

为充分验证本文算法的有效性，我们设计了相关实验，所采用的仿真平台为：Windows10操作系统、64位Intel Core i5处理器、主机频率2.5GHZ、8G运行内存、Matlab2016b.

3.2 算法评价体系及实验设定

在超分辨率的重建过程中，配准精度根据均方根误差(root mean square error,RMSE)[25]这一通用方法来评价,如式(27)，n为配准点数，di为配准后点集与目标点集之间欧式距离的测量值与平均值的偏差:

(27)

对于超分辨率重建结果的评价方法有主观的评价标准和客观评价的标准，本文中采用峰值信噪比(peak signal-to-noise,PSNR)和结构相似性度量(structural similarity,SSIM)作为最后重建的评价指标[27].

(28)

(29)

式(28)中，m,n分别表示图像高和宽的像素数；P为图像像素灰度的最大可能取值，对于一般的灰度图，P=255.PSNR取值范围为[0,+)，其值越高，则认定图像质量越好.式(29)中，μ1，μ2分别为滑动窗口内像素的均值；σ1，σ2分别为滑窗内像素的方差；σ12为两幅图像对应滑窗内像素的协方差；k1，k2为常数，一般设定k1=0.01，k2=0.03.SSIM取值区间为[-1,+1)，其值越大表示图像质量越高.

实验中，设定LR低分辨率序列图像帧数M为4，重建倍数factor为4；在配准点集优化的过程中，根据实际过程中几何运动的程度和图像大小，阈值T1，T2，T3，T4分别设定为70、55、70和55；ICP迭代过程中，RMSE阈值设为0.000001，最大迭代次数设为100，鲁棒损失函数选择Tukey bi-weight函数；NSCT采用1级金字塔分解及4次方向分解，分别采用“maxflat”多尺度滤波器和“dmaxflat7”菱形最大平坦滤波器；融合过程中，低频权值向量ω设为(3/6,1/6,1/6,1/6)，高频硬阈值去噪中的阈值α参考文献[12]设为3.

3.3 实验结果

1)齿科序列图像配准算法验证实验

SIFT (scale invariant feature transform)[28]，即尺度不变特征变换，是一种基于图像局部特征的描述子，通过在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量.为验证ICP配准方法的有效性与准确性，基于测试样本库，将ICP配准法与SIFT特征点配准法进行实验比对.

在测试的200组源图片中，我们发现其中存在11幅图像由于SIFT特征点集的缺少，导致采用SIFT法，不能得出相应的单应变换矩阵；在其他成功配准的齿科图像中，因为齿科图像灰度变化缓慢，分布均匀，造成SIFT特征点提取的不稳定，易收敛于局部最小值.表1中结果说明：SIFT配准法的RMSE明显大于ICP算法求出的结果，而ICP算法稳定性较好，计算复杂度低.

表1 SIFT配准与ICP配准相关统计结果
Table 1 Statistical results related to SIFT and ICP registration

RMSE平均时间RMSEmaxRMSEminSIFT配准3.2460.053s15.7130.224ICP配准0.4340.045s1.4650.012

2)超分辨率重建算法验证实验

以图4中低分辨率序列图像为例，采用本文算法得到的实验结果如下所示：图4(a)是从低分辨率序列图像中选取的参考帧；图4(b)是在低分辨率序列中，与参考帧存在几何相对运动的第i帧；经过ICP配准算法的迭代计算后，可求出位移变换矩阵，图4(c)给出了对序列图像中第i帧配准后的结果.

在ICP配准的过程中，特征点集的提取与变换过程如图4(d)至图4(f)所示：图4(d)是未优化的配准点集，存在很多干扰点；图4(e)中点集经过优化后，ICP算法的包含关系得到满足；图4(f)显示了点集的配准结果.结合SAI插值法对图4(f)进行处理，得到高分辨率图4(g).对序列中的其他帧采用同样的方法进行配准和插值处理后，得到高分辨率的序列图像，对该序列图像中的每一帧依次进行NSCT变换，并采用基于NSCT变换域的改进融合策略，得到重建后的低频分量和高频分量如图4(h)和图4(i)所示.图4(j)对应于NSCT分解后的频谱图；图4(k)为重建结果；图4(l)为真值图.在该例中，ICP配准结果的均方根误差RMSE为0.4634，重建结果的PSNR和SSIM分别为37.029和0.909.

图4 典型案例重建算法示意图Fig.4 Reconstruction steps for a typical case

图5 3组实例对应低分辨率序列与Ground Truth图Fig.5 Corresponding LR sequence and Ground Truth diagram

3)超分辨率重建算法比对实验

为了充分显示本文算法的有效性与优越性，现结合图5实例分析对比4种算法重建结果：1)直接采用cubic插值法；2)对序列低分辨率图像采用本文中的改进ICP算法进行帧间配准，配准后的序列图像采用SAI插值算法，然后在Contourlet变换域(contourlet transform,CT)中，采用与本文算法相同的融合策略完成序列图像的超分辨率重建；3)对序列低分辨率图像采用SIFT算法进行帧间配准，配准后的序列图像采用SAI插值算法，然后在NSCT变换域中，采用与本文算法相同的融合策略完成序列图像的超分辨率重建；4)本文所提出的超分辨率重建算法.

实验结果如表2所示，表2中每一例的第一行对应PSNR值、第二行对应SSIM值.

表2 不同算法实验结果
Table 2 Evaluation results of different algorithms

CubicICP+SAI+CTSIFT+SAI+NSCTICP+SAI+NSCT例132.72335.98820.81536.0880.8110.8860.7590.890例234.09237.24319.15737.9830.8380.9110.8210.930例334.22838.42838.48138.8090.8200.8840.8920.901

由实验数据可知，3例LR图像经cubic插值，重建后的HR图像PSNR和SSIM都较低；而采用方法2后，通过ICP配准和在Contourlet变换域中完成序列图像的融合，评价指标明显上升；方法4即本文算法，将Contourlet变换改成NSCT后，PSNR和SSIM得到了进一步提高，图像效果更佳；如果将方法4中的改进ICP配准算法变更为SIFT特征点配准算法，即方法3，当配准精度与ICP配准相当时，如例3重建结果表现良好，例1和例2则由于配准误差较大，使得重建的指标急剧下降，PSNR只有20.815和19.157.

通过实验比对分析，本文所提出的算法取得了最好的实验效果.其中，改进ICP算法和基于NSCT变换域的融合策略较其它算法，在齿科序列图像的超分辨率重建过程中，具有一定的优越性.

4)测试图库统计分析结果

为定量分析本文算法的有效性，使用超分辨率重建算法比对实验中所提及的4种不同算法，对200张由源图像生成的800张测试图像进行了超分辨率重建，并统计了重建后的评价指标.齿科序列图像重建结果的峰值信噪比PSNR如图6所示：其中横坐标是PSNR峰值信噪比；纵坐标是对应PSNR值下的样本个数；白灰条形图表示cubic双三次插值重建样本数(方法1)；浅灰条形图表示使用ICP配准、SAI插值、Contourlet变换域融合重建的样本数(方法2)；深灰条形图为SIFT特征点配准、SAI插值然后采用NSCT分解融合的重建样本数(方法3)；黑色条形图表示的是本文提出算法的重建样本数(方法4).

由图6可以看出，cubic插值法重建结果(方法1)相对于方法2和方法4的重建结果，其PSNR值分布在较低数值段；而比对方法2和方法4，即基于Contourlet变换域融合与基于NSCT变换域融合的实验对比中，即使采用相同的融合策略，在较高PSNR值区间内，方法4所对应的重建样本数明显多于方法2所对应的重建样本数；另一方面，比对方法3和方法4，即都在NSCT变换域中进行融合时，虽然有些通过SIFT特征点配准算法所得的重建结果与通过ICP配准算法所得重建结果在PSNR值上相当，但是由于SIFT配准在齿科图像应用上效果的不稳定性，使得方法3所对应的PSNR值在图6上呈现出零散分布的状态.因此，综合稳定性与峰值信噪比来看，本文算法有效提高了齿科图像的重建效果.

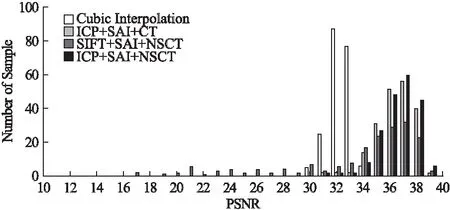
图6 四种不同超分辨率重建算法重建结果PSNR分布Fig.6 PSNR statistical distribution of 4 different SR algorithms

基于构建的齿科低分辨率图像库，表3分别列出了4种不同重建算法重建结果的平均指标，包括峰值信噪比PSNR、均方根误差MSE和结构相似性度量SSIM.可以看出，cubic插值算重建效果最差，PSNR为33.275，SSIM为0.824；而当采用方法2，即采用ICP配准、SAI插值和Contourlet变换融合时，相应指标明显上升，低分辨率序列图像信息得到了有效利用；但是相对于NSCT，CT变换过程中由于存在下采样的过程，不可避免会损失图像信息，细节等，NSCT就表现出更优的效果.

表3 不同超分辨率重建方法的平均精度对比
Table 3 Average indicators comparison of different SR reconstruction methods

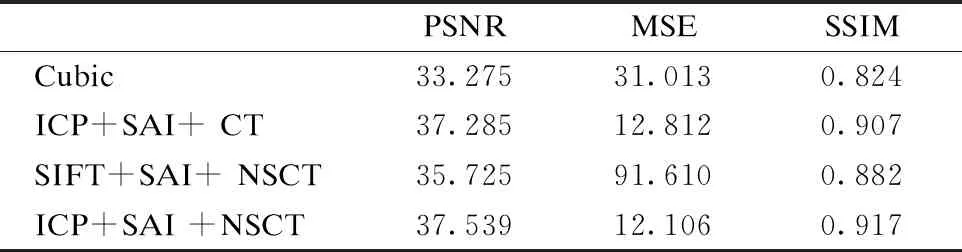
PSNRMSESSIMCubic33.27531.0130.824ICP+SAI+CT37.28512.8120.907SIFT+SAI+NSCT35.72591.6100.882ICP+SAI+NSCT37.53912.1060.917

另外，重建结果的好坏还严重依赖于配准的精度，SIFT在齿科图像重建过程中，由于特征点的缺少和误匹配的存在，导致了方法3整体上劣于方法4，即本文提出算法.本文所提出针对齿科低分辨率序列图像重建的方法，无论是在精度上还是稳定性上都有较大的优势.

3.4 实验结果分析与讨论

通过对实验结果的分析，本文所提出的超分辨率齿科序列图像重建算法，能够有效提高重建高分辨率图像的表现及客观指标，其主要原因在于：

1)经典ICP配准法要求目标点集与源点集存在包含关系，本文则提出了改进ICP的配准策略，引入了鲁棒损失函数，又优化了点集的筛选，使得低分辨率序列图像的配准精度得到了有效保证，同时跟SIFT特征点配准法相比，明显鲁棒性较强；

2)软判决自适应插值法的应用，有效保护了图像的空间一致性，边缘以及牙齿图像细节等信息；

3)NSCT变换相对于傅里叶变换、小波变换等，利用类似轮廓段的结构表征图像，具有良好的稀疏特性，同时由于没有下采样过程，图像保留细节的能力加强；

4)对NSCT变换后的系数进行了有效融合，低分辨率序列图像重建主要重建参考帧，低频融合时加强了参考帧所占比重；高频融合时，硬阈值的去噪可以降低噪声，然后又采用取绝对值最大的方法融合，实现信息的有效互补，整体提高超分辨率的重建效果.

但是从测试样本库的重建结果来看，基于本文所提出的超分辨率齿科序列图像重建算法仍存在不足之处，主要如下：

1)基于点集配对的ICP配准法，仍然无法做到完全的正确配对，同时干扰点的存在会影响配准结果；

2)多分辨率多尺度的变换不可避免的会损失一些图像信息，另外由于既要去除噪声，又要充分保留图像信息，而且序列间的互补信息需要有效融合，之间的权衡关系无法做到完全精准，因此本文所提出的融合策略需要进一步加强.

4 结束语

本文提出了一种基于齿科序列图像的超分辨率重建算法，该算法首先对低分辨率的齿科序列图像进行预处理，减少光照的影响；然后选取牙体硬组织的边缘点作为特征点集，通过改进的ICP配准法，在点集筛选和迭代策略上进行创新，引入鲁棒损失函数，以此矫正低分辨率齿科序列帧间的几何运动，有效减少了偏差较大点的干扰；其次，已配准的序列图像选取有边缘保护作用的SAI插值法放大后，基于超分辨率重建参考帧的特点，通过调整NSCT变换域的去噪与融合策略，实现信息的有效互补，最后利用NSCT的反变换得到超分辨率齿科图像的重建结果.实验结果表明，不论是主观视觉效果上、还是峰值信噪比、结构相似性等客观指标上，本文算法都能够有效提高齿科序列图像的超分辨率重建效果.