考虑级联失效的有向WSNs节点重要度评估模型
邓玉静,王倩悦,尹荣荣,刘 彬
1(燕山大学 信息科学与工程学院,河北 秦皇岛 066004)2(燕山大学 电气工程学院,河北 秦皇岛 066004)
1 引 言
近年来,随着无线通信技术及传感器设备的发展,采用大量具有传感、处理和无线通信能力的传感器节点来监视指定传感领域的无线传感器网络(Wireless Sensors Networks,WSNs)被广泛应用在智能交通、智慧城市、工农业控制及生物医疗等控制领域[1,2].现实世界中的网络多数是有向无标度网络,即度分布服从幂律分布的非同质拓扑结构的有向网络,如食物链网络[3]和引文网络[4].当网络面对随机攻击时,无标度网络比随机网络的抗毁性更强,而当网络面对蓄意攻击,尤其是攻击关键节点时,无标度网络的抗毁性异常脆弱.这是由于当无标度网络中5%的重要节点受到攻击时,会引发节点的级联失效致使整个网络快速崩溃,降低网络的抗毁性.因此,建立能够判定网络关键节点的算法,并对关键点进行针对性的分析和维护,有助于提高整个网络的可靠性与抗毁性[5,6],这也就使网络关键节点的判定研究成为研究者们关注的热点.
目前,对于有向无线传感器网络的关键节点判定问题,研究者们做了大量研究.文献[7]利用引文分析方法,根据超文本中链接结构计算网络中每个网页的被访问频率,提出了PageRank算法,该算法成功地设计了可伸缩的搜索引擎Google.文献[8] 基于扩展哈希技术和网页的唯一访问数,使用基于哈希的索引数据结构动态地对web查询进行分类,提出了一种改进的PageRank算法对web页面进行排序.文献[9]针对传统PageRank算法精度不高的问题,提出一种逆向随机游走PageRank算法,该算法具有更好的稳定性,并在迭代次数较少时也能保持较高精度.文献[10]考虑到有向网络的方向特性的问题,基于网络基序和多元统计分析,提出了一种新的方法来描述有向生物网络中节点的重要性,为进一步挖掘有向生物网络中未发现的节点特征提供新方法.文献[11]为了分析有向通信网络的中间节点的重要性,提出一种以节点表示端到端路由的快速寻找算法,该方法运算简单,具有一定的实用性.文献[12] 建立了一种度量加权有向网络中节点中心度的指标,以有向度中心性为初始值,引入了异步更新过程,迭代使用更多的网络信息更新节点的重要性.文献[13]考虑多种指标,构建了三种影响力矩阵,采用层次分析法构建了有向加权网络模型节点重要性评价方法.然而,以上节点重要度的评估方法皆局限于节点间的相互独立性,未考虑网络传输负载的时变动力学特征.当节点的负载大于其容量时,节点出现故障,则其负载会被分配到其他节点上,这就加剧了其他节点的负载压力,而当邻居节点的负载超过自身容量时也会失效,产生级联故障传播,造成大规模网络的瘫痪[14].针对这个问题,文献[15] 考虑级联失效局域信息,构建了最近邻分配和全局分配两种规则的复杂网络节点重要度判定模型.文献[16]针对级联失效问题,建立了一种重载函数模型,提出了一种考虑级联失效的节点重要性评估方法,可以找到一些潜在的关键节点.文献[15,16]虽然考虑了节点间相互影响可能会造成的级联效应,但是没有考虑网络的方向性特征.
以上研究虽然取得了一定的成果,但均未综合节点之间的相互影响以及节点之间相互影响的方向性.针对以上问题,本文在有向无线传感器网络中基于级联失效对节点重要度进行分析.首先,考虑网络节点层级关系、负载、容量及负载重分配规则,建立有向网络级联失效模型,并推导出节点失效后引起的负载震荡状态值.然后,引入经典Pagerank算法,建立节点度择优的分配规则对其平均分配规则进行改进,将失效节点引发的邻居节点平均负载震荡状态值作为节点的初始重要度值,构建考虑级联失效的有向无线传感器网络节点重要度判定算法——NCFD(Noderank considering cascading failure in directed wireless sensor networks).最后,通过实验仿真验证算法的有效性.
2 有向网络级联失效模型
本节考虑无线传感器网络中节点的负载、容量和负载重分配规则三种因素,对有向网络级联失效进行建模,分析有向网络的级联失效过程.运用数学公式,推导得到节点失效后在其分配范围内引起的负载和能量的震荡状态值,为下一节构建级联失效相关的节点重要性评估模型奠定基础.
2.1 级联失效模型
现实生活中很多网络都是有向的,例如无线传感器网络中数据在实际传输过程中总是朝着基站方向传播,网络中的节点由sink节点和普通节点组成,而处于不同层级的节点所承担的负载也不同.本文按照网络中普通节点到sink节点的跳数对网络拓扑进行分层.有向网络分层结构如图1所示,按照图1网络中的数据传输方向,处于n层的节点是处于n-1层节点的父节点,相应地,处于n-1层节点是处于n层节点的子节点(如2号节点是8号节点和12号节点的子节点;相应的8号节点和12号节点均为2号节点的父节点).
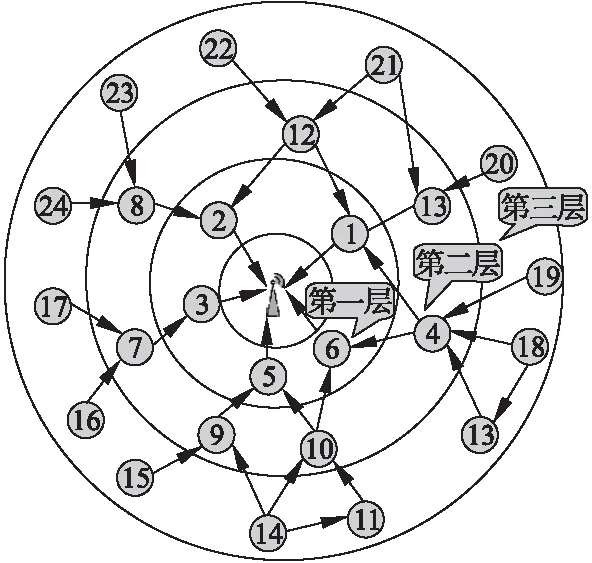
图1 网络分层示意图Fig.1 Layered network
根据有向分层网络拓扑结构特性,节点的入度越大,说明其接收的数据量越大,其负载也会相应的增大.而当邻居节点的入度较大时,邻居节点传输过来较大的数据量也会增加节点的负载.因此,本节考虑节点的层级关系、节点入度以及邻居节点的入度对节点的影响来定义节点负载的非线性函数,具体表达式如下:
(1)
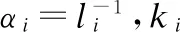
节点的容量是节点能够承担负载的极限值,根据ML模型,节点容量与其初始负载呈正比关系,即:
Ci=(1+τ)Li,τ≥0
(2)
其中,Ci是节点i的容量,τ是网络的能力容量参数,表示节点处理额外负载的能力,Li是节点i的初始负载.
图2 有向网络级联失效后的负载重分配示意图Fig.2 Load redistribution after cascade failure in directed networks
由图2的有向网络可以看出,当节点i意外失效后,来自其父节点j1,j3的数据将无法流入,同时流出到其子节点j2的数据也将被中断.这就导致父节点j1,j3的负载以一定的分配规则被重新分配给其父节点或其他的子节点,也将导致这些节点因过载而失效,此过程循环进行,直到网络中的再分配节点不出现过载现象.同时,而子节点j2无法接收来自i的数据,会因数据少载而被禁用.最终,这两种失效现象导致大规模网络崩溃.
根据有向网络节点数据传输的方向性,当节点i失效时,其负载将返回给其父节点,也可能会转移到该父节点的其他子节点.父节点j增加的负载将按照公式(3)所示的负载重分配规则进行分配[18]:
(3)
当节点i失效时,其子节点因无法接收其传输过来的数据而导致负载减少,根据子节点的承载能力,子节点w减少的负载将按照公式(4)所示的负载重分配规则进行分配:
(4)
因此,根据以上原则,节点i失效后,它的父节点负载更新为:
(5)
子节点负载更新为:
(6)
上述是一次有向网络失效节点的负载重分配的过程.节点负载更新完成后,若节点j的负载超过其容量,则节点j也会因过载而失效,网络将进行新一轮的负载重分配,而新的负载重分配将导致更多节点失效,形成级联失效,负载重分配一直进行到网络中没有负载过载现象停止.
2.2 级联失效震荡状态值
若使节点j不会引发后续的级联失效,则其负载更新之后该满足如下条件:
Lj+ΔLj→i≤Cj
(7)
根据公式(1)和公式(2),上面的不等式可以细化为:
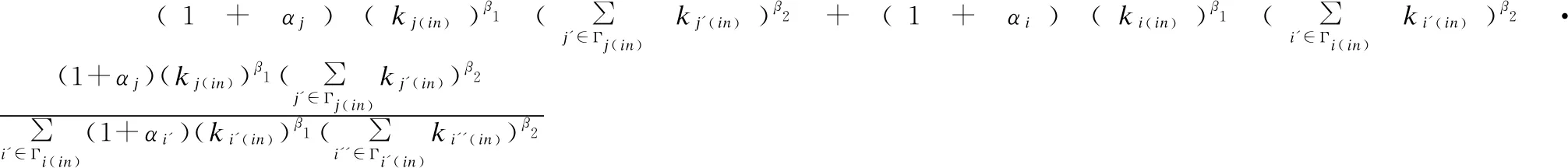
(8)
化简为:
(9)
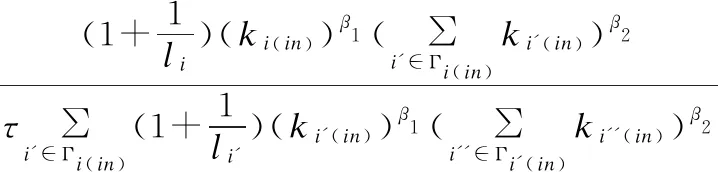
(10)
若F(i)的值大于1则节点j过载,若F(i)的值小于或等于1则节点j不过载.
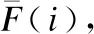
(11)
3 节点重要度评估方法建立
本节借鉴PageRank算法[15]的网页连接价值重要性排名的思想,结合上一节推导得到的级联失效震荡状态值,建立考虑级联失效的有向无线传感器网络节点重要性评估模型NCFD.
PageRank算法是用于搜索引擎中网页排序的经典算法.其数学公式如下:
(12)
其中,PR(x)为网页x的重要度值;σ为阻尼系数;n为指向x的网页数目;PR(Yi)为指向x的网页Yi的重要度值;Cout(Yi)为Yi的出边数量.由公式(12)可以看出,当n越大,x的链接源越多,PR(Yi)越大,指向x的网页的重要度越高,则网页x越重要.
现实网络中节点因所处的层级、负载及容量不同而其对应的重要度也不同.PageRank 算法的平均分配思想,在一定程度上降低了节点重要度的排序准确率.因此,本文将每一个节点的初始重要度定义为节点级联失效后引起的平均震荡状态值,同时将其按照节点度所占比例进行分配.在有向网络G(V,E)中,节点数N=|V|,节点v与节点v1,v2,…,vf相连,则节点v的重要度NR(v)为:
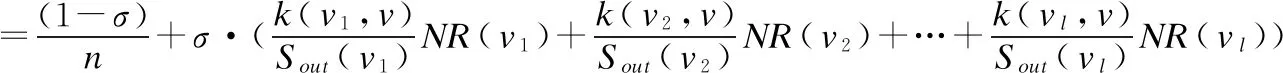
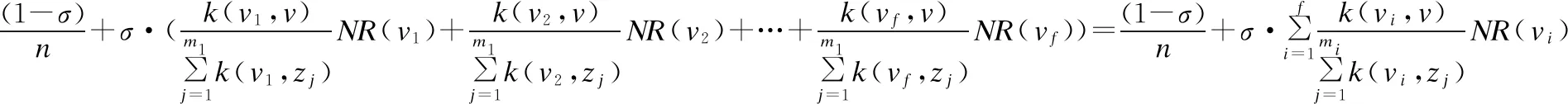
(13)
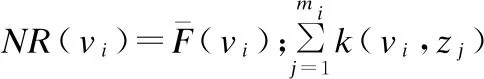
NCFD计算各个节点的重要度的算法步骤如算法1所示.

算法1.NEIAlgorithm输入:AdjacencymatrixA=(aij)N×NofdirectednetworkGwithNnodes输出:TheorderSofnodevStep1.Initializetheloadadjustableparameterandcapacityparameter,andcalculatetheinitialloadandcapacityofthenodebyEq.(1)andEq.(2).Step2.Deletenodev.Step3.UpdatenodeloadbyEq.(5)andEq.(6).Step4.Judgewhetheranewfailurenodeisadded,ifso,deletethefailurenodeandreturntoStep3,otherwiseturntoStep5.Step5.CalculatetheaverageoscillationstatevalueF(i)byEq.(11).Step6.CalculatetheimportanceNR(v)ofnodev.Step7.Whetherallnodesaretraversed,ifso,turntoStep7,otherwise,selectdifferentnodespandreturntoStep2.Step8.S=SortvbyNR(v).
4 仿真实验
本节仿真实验中,首先对比分析PageRank算法与本文NCFD算法所判定出无标度网络的节点重要度,然后分别采取删除两种算法判定的关键节点和保护所判定出的关键节点两种措施下的网络抗毁性进行分析和评估,以验证本文所构建模型的准确性和合理性.本实验的实验结果均取50次实验的平均值.具体的实验环境参数见表1.
表1 NCFD实验数据表
Table 1 Experimental parameters
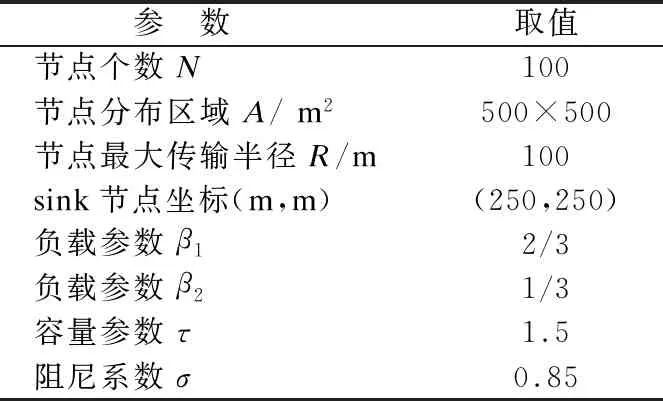
参 数取值节点个数N100节点分布区域A/m2500×500节点最大传输半径R/m100sink节点坐标(m,m)(250,250)负载参数β12/3负载参数β21/3容量参数τ1.5阻尼系数σ0.85
4.1 节点重要度分析
在图3所示的网络拓扑结构(其中sink节点在监测区域的正中心)上,分别根据公式(12)和公式(13)计算PageRank算法和本文NCFD算法的节点重要度值,并绘制出如图4所示的节点的重要度分布图.
由图4中可知,PageRank算法与本文NCFD算法判定出的节点重要度分布趋势一致,节点5,23,25,68,74,86,89,90,92,93,94,95,97,98都是网络中的重要节点,验证了本文NCFD算法的有效性.本文NCFD算法判定出节点8,28,60,80,87,100的重要性也较高,这是由于本文考虑了节点失效引发级联失效的震荡程度以及节点所处不同层级的因素,这些节点失效极有可能触发节点间的“级联效应”,加速网络崩溃.说明本文NCFD算法能够判断出网络中潜在的关键节点,使得节点重要度的判定更加全面.
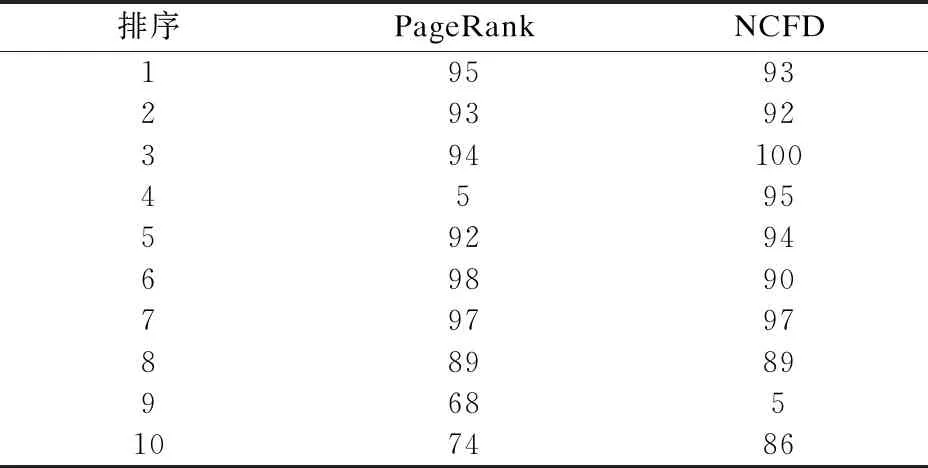
由表2可知,PageRank算法中重要度值最高的节点是95号节点,而其在NCFD算法中排名仅为第4.在NCFD算法中100号节点重要度值排名第3,而PageRank算法中其排名并未进入前10.这是由于NCFD算法考虑了节点失效后引发的级联震荡的作用.由于95号节点的震荡状态值较93号节点低,所以其重要度低于93号节点,而100号节点的震荡状态值较高,其失效后引发网络级联失效的可能性很大,所以100号节点重要度较高.因此,NCFD算法判定的结果更加全面.
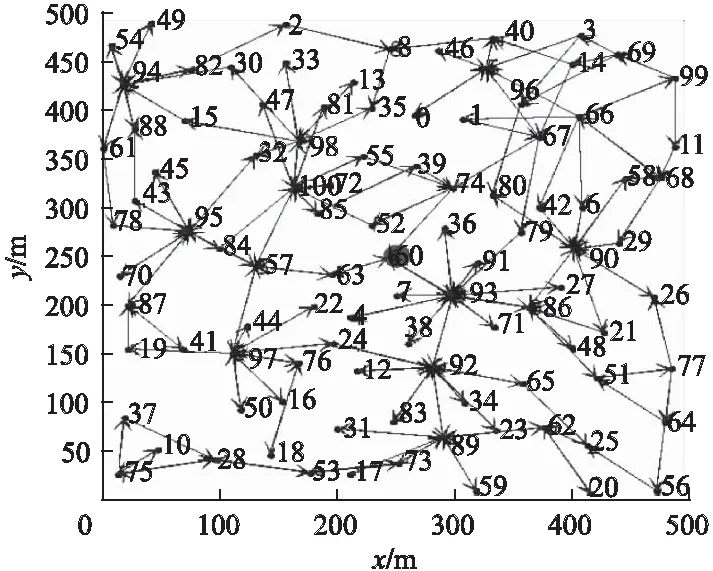
图3 网络拓扑结构Fig.3 Network topology
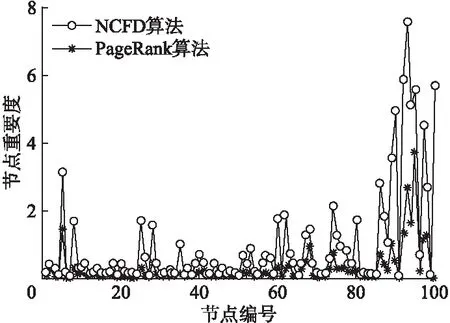
图4 节点重要度分布Fig.4 Node importance distribution
4.2 网络抗毁性分析
统计PageRank算法和本文NCFD算法所判定出的节点重要度排名靠前的10个节点,排序结果如表2所示.
表2 节点重要度排名前10的节点编号
Table 2 Node numbers with node importance in Top 10
排序PageRankNCFD19593293923941004595592946989079797889899685107486
为了进一步验证算法的准确性与合理性,分别按照两种算法所判定出的重要度顺序逐次移除节点,并观察包含sink节点的连通块中节点数目的变化情况,统计结果如图5所示.
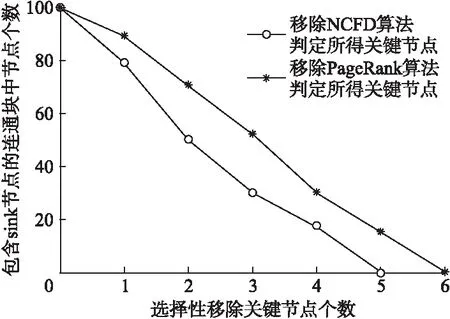
图5 移除关键点后连通块的变化情况Fig.5 Change of connected block after removing critical nodes
由图5中可知,选择性移除两种算法所判定出的关键节点,包含sink节点连通块中节点数目均呈下降趋势,且NCFD算法的下降速度明显较快.当移除4个关键节点时,PageRank算法的网络连通块中节点数目约为35%,而NCFD算法已经少于总节点数目的20%了.这是由于NCFD算法不仅对PageRank算法平均分配的不合理性进行了改进,而且考虑一个节点失效可能引发的网络级联失效效应,引入了级联失效震荡状态值参数,使得判定结果减少了遗漏关键点的情况.
下面分别对网络中由两种算法所判定出的重要度排名前10的节点采取保护措施,然后逐次随机移除网络中的节点,并观察网络中包含sink节点的连通块中节点数目的变化情况,统计结果如图6所示.
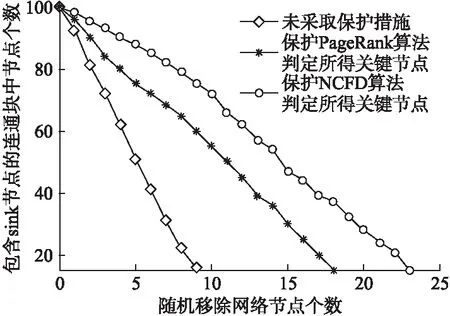
图6 随机移除下连通块的变化情况Fig.6 Change of connected blocks under random removal
由图6可知,面对节点随机失效,保护由NCFD算法所判定出的关键点时,网络的容忍力均比保护PageRank算法和未采取保护措施时强.随着网络中失效节点数量的增加,保护由NCFD算法所判定出的关键点时,网络中包含sink节点的连通块节点数目下降速度最慢.而且,当随机移除20个节点时,可以看出包含sink节点的连通块中仍有30个节点,而在另外两种措施下,网络包含sink节点的连通块的数目均远少于30个.同时图6也说明了保护由NCFD算法判定所得关键点比保护由PageRank算法判定所得关键点的网络能表现出更强的抗毁性,这也进一步验证了NCFD算法的准确性.
5 结 论
本文针对目前无线传感器网络节点重要性评估方法中未综合考虑节点之间相互作用及数据传输具有方向性的问题,提出了考虑级联失效的有向WSNs节点重要性评估模型.通过Matlab仿真实验验证了该方法能有效地评估有向无线传感器网络节点的重要性.而且采取选择性移除和随机移除两种攻击下本文NCFD算法可以明显地增强网络的抗毁性,因此,本文构建的有向WSNs节点重要度评估模型及级联失效模型可以为提高网络鲁棒性研究提供理论支持.本文仅采用了Matlab仿真实验进行验证,如何在实际网络中验证及应用将是下一步的研究工作.

