自适应强跟踪卡尔曼滤波器载波环设计*

王福军，丁小燕，王 前，白英广

（1.北京卫星导航中心，北京 100094；2.河北省科学院地理科学研究所河北省地理信息开发应用工程技术研究中心，石家庄 050000）

0 引言

载波跟踪环路是卫星导航接收机设计的核心环节，载波跟踪环路设计要同时考虑动态适应性和跟踪精度指标，自适应跟踪技术能够较好地解决这个问题。传统载波跟踪环路自适应跟踪技术主要有两类，一类是锁相环变环路带宽技术，通过在线检测和估计信号和噪声模型参数，自适应地调整锁相环路等效噪声带宽［1-2］。另一类是以锁相环和锁频环组合为代表的自适应阶数技术。通过实时鉴频判断经验门限硬选择，或自适应调整权重来确定锁相环和锁频环在载波跟踪环路中作用［3-5］。自适应跟踪技术在一定程度上能够改善传统跟踪环路的动态性能和稳定性，但是传统跟踪环路是在S 域建立对噪声和信号的建模，对动态应力、晶振抖动等非平稳过程建模困难，因此，基于模型的自适应跟踪技术通常无法达到最优且不稳定，而且，在跟踪过程中无法得到预测的跟踪状态误差，实现自适应跟踪。

卡尔曼滤波算法能够很好地对信号进行估计和预测，而且对跟踪环路中的信号很容易建模，近年来在GNSS 载波跟踪环路中得到广泛应用。根据观测量的不同可以分为两类：一类是用鉴别器输出结果作为观测量，状态方程和观测方程均为线性的［6-7］；另一类直接用IQ 支路相关积分结果作为观测量，观测方程为非线性的［8-10］。两类卡尔曼滤波算法的优异性能均是建立在对载波跟踪环路的准确建模和噪声模型参数的准确估计基础上的，否则，卡尔曼滤波器的性能就会下降甚至发散。因此，同样需要研究适合应用到GNSS 载波跟踪环路的自适应卡尔曼滤波技术。

线性自适应卡尔曼滤波算法具有实时性好、可靠性高、易于在基带处理中实现等优点。本文结合线性模型的自适应Qk/Rk算法［10］和强跟踪算法［7-9］，提出了一种线性自适应强跟踪滤波算法。在稳态运动场景下，采用自适应Qk/Rk卡尔曼滤波滤波器跟踪环路，实现自适应场景噪声变化，当场景切换时，利用强跟踪技术提高跟踪环路鲁棒性。

1 基于卡尔曼滤波器的跟踪环设计

1.1 状态转移方程和观测方程

跟踪环的状态转移方程可表示为

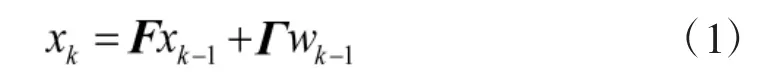
qk为载波多普勒频率变化率噪声（即多普勒频率二次变化率）功率谱密度，可以根据载波相位动态性进行估计。

观测方程可以表示为

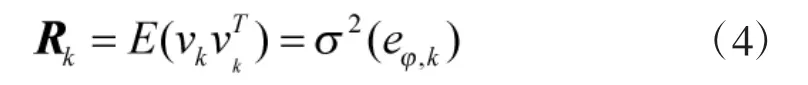
1.2 卡尔曼滤波器模型

则xk的估计可按下述过程求解：

1）时间更新方程

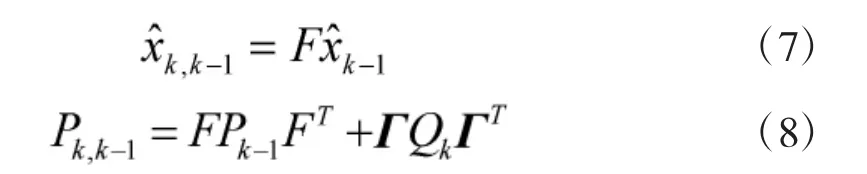
2）测量更新方程

1.3 数控振荡器（NCO）更新

NCO 控制量应该与第k+1 步环路输入信号相位匹配，其中载波频率估计可以由式（11）求得，但第k+1 步的卡尔曼增益和测量残差在第k 步是未知的，可以认为第k 步和第k+1 步的卡尔曼增益和测量残差近似不变，则第k 步输入的NCO 控制量表达式为［13］

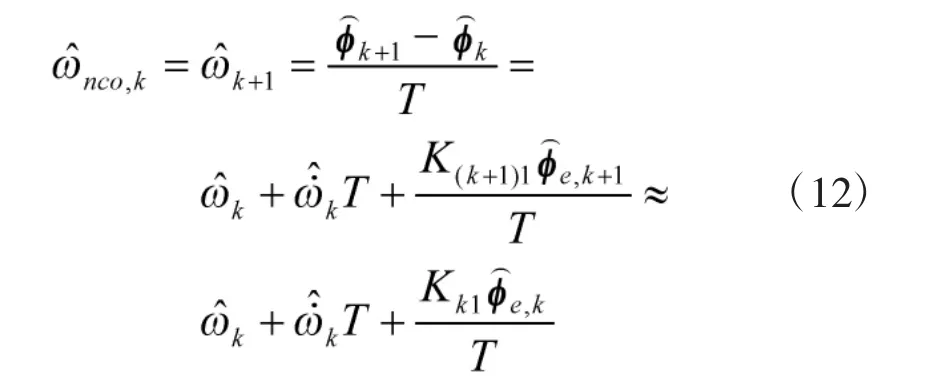
1.4 小结

对于标准卡尔曼滤波，在初始时刻，卡尔曼增益和估计误差依赖于先验估计误差的协方差P0和观测噪声方差Rk的相对权重，即P0/Rk，为了保证环路的鲁棒性，通常会取一个比较大的P0，此时环路等效噪声带宽和卡尔曼增益Kk比较大。随着跟踪算法的递推，初始时刻的P0值估计误差将被快速校正并收敛，环路等效噪声带宽和卡尔曼增益随着P0/ Rk的减小而下降。当跟踪环路进入稳态区域后，P0值稳定，其值取决于过程噪声协方差Qk与和观测噪声方差Rk的相对权重，即Qk/Rk。研究表明［7］，当环路稳定后，卡尔曼滤波器与3 阶PLL等价，其增益为：

因此，标准卡尔曼滤波不具备自适应等效噪声带宽的能力。

2 自适应跟踪技术

2.1 算法分析

载波跟踪环路的最终设计目标是在保证稳定跟踪的同时，在尽量多的时间内具有较高的跟踪精度，也就是说，自适应卡尔曼滤波要解决两个问题，一是在场景切换时滤波器要具有稳健的跟踪能力；二是在场景稳定后滤波器又具有较高的跟踪精度。针对第1 个问题，通过上面对标准卡尔曼滤波器工作原理分析可知，在初始时刻，通过选取比较大的P0值可使环路具有较大的等效噪声带宽，因此，可以将场景切换过程类似于初始阶段，通过强制调整Pk值来改变环路等效噪声带宽。强跟踪滤波器就是通过实时估计新息统计量调整状态预测误差的协方差矩阵Pk，提高环路的稳定性。针对第2 个问题，稳态跟踪精度主要依赖于与场景相匹配的Qk/Rk值，不同场景的Qk/Rk一般是不同的，为了保证稳态跟踪精度需要实时在线估计Qk和Rk。自适应Qk/Rk卡尔曼滤波算法能够给出Qk和Rk值的估计。

2.2 强跟踪卡尔曼滤波算法

强跟踪滤波器是针对扩展卡尔曼滤波器对系统模型不确定性、初始状态统计不准确和应对突变等不确定因素鲁棒性较差而提出的［8］。它通过实时估计新息统计量调整状态预测误差的协方差矩阵以及相应的增益矩阵，强制使不同时刻的新息序列保持相互正交，即将基本卡尔曼滤波器递推方程中的式（8）修改为

式中，Pek为卡尔曼滤波新息协方差，其值为

滑动窗口宽度m 可以根据实际场景需要确定，窗口宽度越大，估计值越准确，但算法响应能力越差。

2.3 自适应Qk/Rk 卡尔曼滤波算法

目前应用比较广泛的基于极大后验（MAP）估计准则的sage-Husa［14］方法能够对Qk和Rk值进行无偏估计，但该方法很容易引起发散，且对初始条件的选取非常敏感［15］，如果应用到载波环路中需要增加条件限制。本文参考文献［10］提出Qk值改进估计方法，其表达式如下：

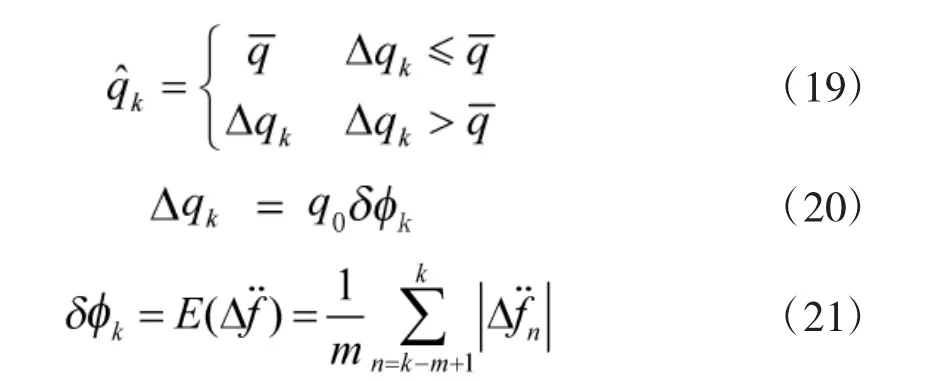
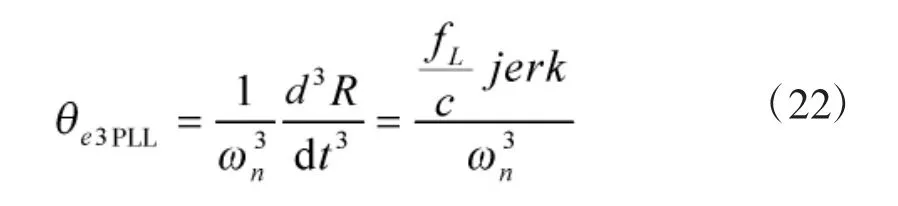
式中，θe3PLL量纲为Hz，fL为载波频率，c 为光速，jerk为动态信号的视距加加速度，则载波多普勒频率二次变化率为：

综合式（14）、式（23）和式（24）可得

测量噪声矩阵Rk可以通过载噪比来估计［7］：

式中，（C/N0）k可以根据信号加噪声的功率在不同噪声带宽上的差异进行估计［12］，计算方法为

式中，Pwb（k）为带宽为1/Tcoh的宽带带宽功率，Pnb（k）带宽为1/（MTcoh）的窄带带宽功率，Pnw（k）窄带功率Pnb（k）与宽带功率Pwb的比值，μp为k 个时刻Pnw（k）的平均值，主要为了降低比率的噪声量，Tcoh为相关积分时间，M 值和K 值根据经验确定。

2.4 小结

通过以上分析，自适应Qk/Rk卡尔曼滤波算法能够实时在线估计系统噪声方差Qk和观测噪声方差Rk，相比标准卡尔曼滤波，具有较好的跟踪精度和一定的动态适应性。但是，当初始参数设置误差较大或载体进行剧烈运动场景切换时，由于算法对Qk值和Rk值估计收敛速度慢，跟踪环路仍然可能失锁，因此，算法适合载体运动状态变化不剧烈的运动场景内跟踪。而强跟踪算法是在载体运动状态剧烈变化时，通过强制调整状态预测误差的协方差矩阵以及相应的增益矩阵，提高算法鲁棒性。当载体运动状态剧烈变化结束后，仍然通过初始设定的固定Qk值和Rk值对载体进行跟踪，一般不同运动场景的Qk值和Rk值是不同的，因此，不能保证跟踪精度，该算法适合载体运动场景切换时的暂态跟踪。

针对以上问题，本文提出了自适应强跟踪滤波算法。通过实时在线估计新息y～k统计量，根据新息y～k统计量大小调整Qk值、Rk值、Pk，k-1值以及相应的增益矩阵，因此，算法既能保证跟踪环路跟踪精度，也提高了动态适应性。

3 仿真与比较

本文用于GPS L1 频点信号仿真的数据有2 组：实测静态数据和由仿真软件生成的动态仿真数据，中频信号频率为9.548 MHz，采样率为38.192 MHz，环路更新率为1 ms。为了验证本文提出算法的有效性，分别对标准卡尔曼滤波（简称算法1）、强跟踪滤波（简称算法2）、自适应Qk/Rk滤波（简称算法3）和自适应强跟踪滤波（简称算法4）4 种算法进行仿真。为了确保公平性，设置标准卡尔曼滤波和强跟踪滤波算法的qk和Rk值为相同的固定常数q0和R0，自适应Qk/Rk滤波和自适应强跟踪滤波算法的值也设置为q0值。动态场景仿真参数见表1。下页图1～图3 是在不同仿真条件下，4 种跟踪算法的载波相位误差和多普勒频率跟踪效果对比图，图1～图3 中阶段1 的多普勒频率不为0（大约38 Hz），主要是由捕获引起的捕获频率误差。

表1 仿真参数表

图1 仿真条件1 载波相位误差和多普勒频率跟踪效果对比图

图1 为算法1～算法4 对静态实测数据跟踪的载波相位误差和多普勒频率对比图，载波相位误差标准差分别为0.018 42 Hz，0.014 81 Hz、0.018 42 Hz和0.014 81 Hz。从图1 中可以看出，1）在初始阶段，算法1和算法3 跟踪结果完全相同，算法2 和算法4 跟踪结果完全相同，且算法2、算法4 比算法1、算法3 更快进入稳定状态。一是由于载波相位误差大和初始化参数不准确等原因，导致初始载波相位跟踪误差大，算法2、算法4 的自适应衰减因子k 在跟踪过程中发挥了作用，使环路有更宽的等效噪声带宽，因此，能够更快地进入稳定状态；二是由于初始载波相位误差还没有大到使自适应Qk/Rk估计算法认为出现模型外系统噪声程度，因此，算法3、算法4 中的自适应Qk/Rk估计算法没有发挥作用。2）在稳定阶段，算法1～算法4 的跟踪精度基本相同。由于跟踪精度主要依赖于Qk/Rk值，算法1、2 的qk和Rk值为固定常数q0和R0，且R0值是根据实测静态场景的观测噪声方差统计量设置的，接近真实统计量；算法3 和算法4 的模型内系统噪声方差也为q0，实时估计的Rk也接近R0，因此，4 种算法的跟踪精度基本相同。

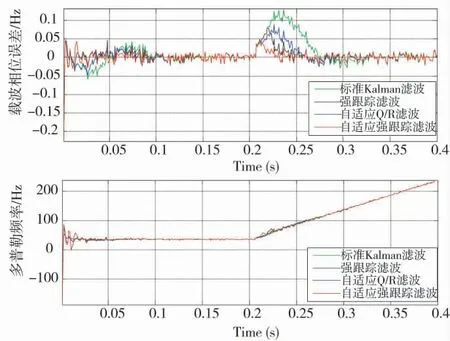
图2 仿真条件2 载波相位误差和多普勒频率跟踪效果对比图

图2 为算法1～算法4 对仿真2 数据跟踪的载波相位误差和多普勒频率对比图，载波相位误差标准差分别为0.036 21 Hz，0.020 01 Hz 和0.023 57 Hz、0.016 83 Hz。从图中可以看出，1）在初始阶段，4 种算法按照跟踪精度（由低到高）、收敛时间（由长到短）、等效噪声带宽（由小到大）指标排序依次为算法1、算法3、算法2 和算法4。算法3 好于算法1 是由于自适应Qk/Rk算法实时估计的Rk值更接近真实值；算法2 好于前两种算法是由于自适应衰减因子k 在跟踪过程中发挥了作用，说明针对较大的载波相位误差，强跟踪算法比自适应Qk/Rk算法更灵敏；算法4 好于前三种算法是由于自适应衰减因子k和自适应Qk/Rk算法同时发挥作用。2）在场景切换阶段，4 种算法的跟踪效果排序与初始阶段相同，不同点是算法3、算法4 中自适应Qk/Rk算法不但实时估计Rk值，而且由于跟踪误差比较大，也估计出存在模型外系统噪声，提高相应的Qk值及等效噪声带宽，进一步提高算法的动态性能。

图3 为算法1～4 对仿真3 数据跟踪载波相位误差和多普勒频率对比图，载波相位误差标准差分别为0.102 8 Hz，0.025 01 Hz、0.105 1 Hz 和0.019 86 Hz。从图中可以看出，在遇到运动状态变化较大的场景切换时，算法1 和算法3 失锁，而算法2 和算法4 仍能稳定跟踪，且算法4 动态适应能力强于算法2。

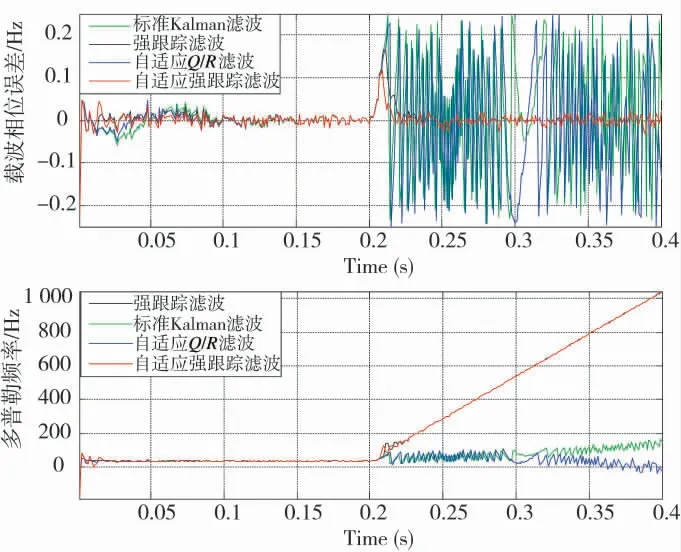
图3 仿真条件3 载波相位误差和多普勒频率跟踪效果对比图

4 结论

本文提出的自适应强跟踪算法对于初始状态统计不准确、场景切换（运动状态突变）和噪声变化等不确定因素表现出良好的滤波性能。利用自适应Qk/Rk滤波算法实时估计和修正噪声统计量来自适应跟踪过程中的噪声变化，引入强跟踪技术有效解决算法对初始值敏感、容易发散等问题。该算法比自适应Qk/Rk滤波算法具有较强的鲁棒性，比强跟踪算法具有较强的噪声自适应性，在GNSS 载波跟踪环路应用中有广阔的前景。