基于Radon 变换的弹道目标平动补偿*

韩立珣，许 丹，田 波，冯存前，王业峰

（1.空军工程大学防空反导学院，西安 710051；2.解放军32147 部队，陕西 宝鸡 721000）

0 引言

弹道导弹防御需要雷达对弹道目标进行识别。近年来，随着电磁技术和诱饵技术的不断发展，传统的雷达目标识别方法存在着一定的缺陷，需要引入新的目标特征进行综合识别［1］。微动是弹道目标在飞行中产生的微小运动，不易模仿，可作为雷达目标识别的新的特征［2-3］。弹道目标运动时，会出现平动和微动两种运动。平动分量与微动分量相互叠加，回波的多普勒曲线由于平动将导致曲线倾斜、平移、折叠，影响微动信息的提取，因此，在进行弹道目标微动特征提取时，需要对其进行平动补偿［4］。

文献［5］用中心法和重心法对含有速度的锥体进动目标进行了速度估计。文献［6］以含有加速度分量的锥体摆动为研究对象，分别利用峰值法和模板法对加速度进行了补偿和仿真比较，验证了补偿方法的有效性。文献［7］通过分析得出了平动近似为多项式，推导了瞬时多普勒极值点与多项式参数和微动参数的关系。文献［8］利用经验模态对强散射点信息进行了分解，得到了平动分量与微动分量，实现了平动分量的补偿。然而上述方法的关键都在于准确地得到某个散射点的多普勒信息，并没有充分利用目标整体的散射点多普勒信息。

考虑到散射点平动分量的一致性，本文从目标整体信息出发，利用Radon 变换对弹道目标时频曲线进行投影变换，通过熵值法和高斯函数拟合估计图像中峰值位置，从而达到平动参数的估计。该方法利用了目标的整体信息，不需要对时频曲线进行分离处理。仿真结果表明该方法的准确性和适应性。

1 弹道目标中段模型

图1 弹头进动模型示意图

在弹道中段中，弹头在诱饵释放的过程中会受到扰动，扰动会使弹头产生进动。如图1 所示，建立弹头进动坐标系O-xyz，以锥旋轴为z 轴，定义初始时刻对称轴与z 轴所在平面为yOz 平面，x 轴方向符合右手螺旋准则。进动角为θ，进动角速度为ωc，锥顶为D，半锥角为ε，锥体高度为h，底面半径为r，锥顶与原点的距离为h1，底面中心与原点的距离为h2。定义雷达视线方向与对称轴构成的平面为底面圆环的电磁波入射平面，该平面与圆环交于p、q 两点，雷达视线与锥体对称轴夹角为β。初始时刻雷达到坐标原点O 的距离为R0且满足远场条件。

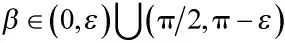
则散射点D、p、q 微动距离变化表达式为：

弹道目标运动主要包括两个部分，一个是高速平动，另一个是具有周期性的微动。由于微动周期较小，当在几个微动周期内对弹道目标运动进行分析时，平动速度可近似为二阶多项式［7］。以散射点D 为研究对象，此时，平动距离为：

其中，v、t 分别为目标t 时刻的速度和加速度。由于弹道目标的速度和径向距离很大，可通过雷达测量值进行预补偿，补偿后的表达式为：

假设雷达发射波长为λ 的单频信号，目标上散射点k 的散射系数为σk，则窄带雷达得到回波基带信号为：

结合式（5）得目标各散射点的微多普勒表达式如下：

2 基于Radon 变换的平动补偿

对式（6）进行时频变换可得到第3 节中的图2，从图中可看出平动分量使散射点微多普勒曲线产生折叠，直接进行参数提取较为困难。但平动导致了微多普勒曲线整体上呈现一次函数倾斜趋势，一次函数的参数与平动参数有关。因此，可以考虑从目标微多普勒曲线整体出发，利用Radon 变换对平动参数Δv 和a 进行估计。

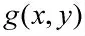
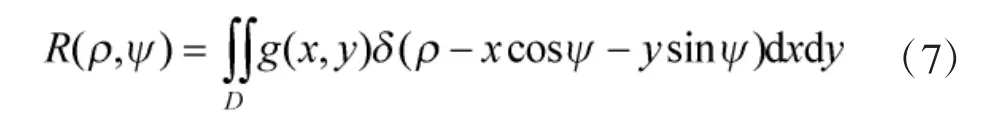
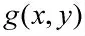
当时频图中曲线数量较多时，各条曲线并不是严格服从相同的线性趋势，这将导致Radon 变换得到的累积亮点散焦，不利于参数提取。因此，在提取参数时引入最小熵值和高斯函数拟合的方法估计平动参数。定义熵：

综上所述，弹道目标平动补偿的步骤为：

1）利用雷达距离和速度测量值对目标回波信号进行预补偿。

3 仿真实验

图2 为该雷达获得的目标回波时频分布，图中三条微多普勒曲线相互叠加，同时由于平动分量的存在，微多普勒曲线出现整体呈现倾斜。图3 为采用Radon 变换对时频图进行处理得到的结果，图4 为熵值与变化关系图，可得到的参数估计值=3.17 和=82.46 后，由式（9）可以计算得到平动参数Δ=4.12 m/s，=1.88 m/s2，与理论值较为接近。设平动补偿函数为，将代入式（10）中进行补偿。图5 为补偿后的时频图，可以看出曲线的折叠和倾斜得到了消除，补偿效果较好，证明了本文方法的有效性。

图2 目标回波时频图

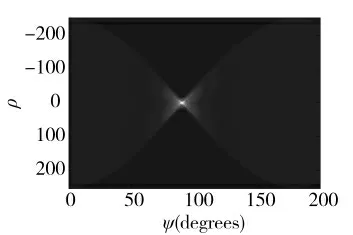
图3 Radon 变换结果

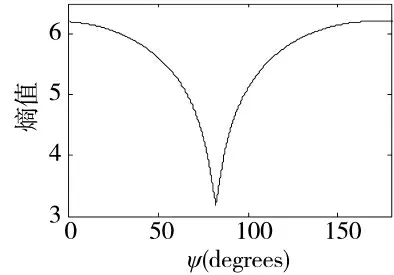
图4 熵值与变化关系

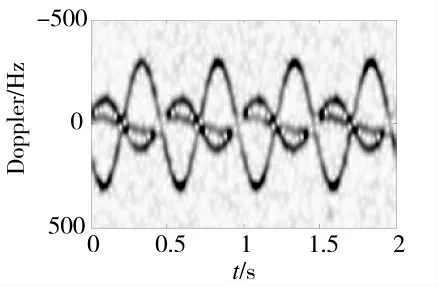
图5 平动补偿后的时频结果

在信噪比（-6 dB，6 dB）之间以2 dB 为间隔进行蒙托卡罗仿真，每一个信噪比条件下采用100 次仿真实验，仿真结果如表1 所示。

表1 平动参数估计性能

可以看出本文提出的方法相对文献［7］的方法而言，参数估计的性能更好，特别是在低信噪比情况下尤为明显。原因是文献［7］利用强散射点进行分析，只利用了一小部分的目标回波信息，而本文提出的利用Radon 变换提取整个微多普勒曲线的倾斜系数，拟合出目标的平动参数，这一方法利用了更多的回波信息，从而可以获取更加精确的参数估计值。

仿真实验均在同一台计算机（CPU 为Intel Core i5 3.3 GHz，内存为4 GB）上进行处理，文献［7］所提的算法在参数提取上平均用时1.039 s，本文所提算法在参数提取上平均用时0.453 s。

4 结论

本文对多散射点目标的平动补偿问题进行了研究，利用目标整体的平动趋势，采用Radon 变换对目标整体微多普勒曲线进行了参数投影，利用熵值法和高斯函数拟合对平动参数进行了估计。仿真结果表明该方法具有较好的补偿效果，为弹道目标微动参数求解打下了一个基础。由于弹道中段存在着各种诱饵和碎片，下一步将对弹道群目标的平动补偿进行研究。