多维体验,构建数学生态课堂

【摘要】本文以《平行线的性质》教学为例,论述建构数学生态课堂的途径,提出从学生的认知矛盾中展开构建、在体验中关注生成、在理解中形成关联、在应用中建立体验的教学建议,促进数学生态课堂的建设,形成系统性学科认知。
【关键词】初中数学 《平行线的性质》 生态课堂 实践体验
【中图分类号】G 【文献标识码】A
【文章编号】0450-9889(2020)41-0048-02
“两条平行线被第三条直线所截,同位角相等。”这是“平行线的性质”,教师在执教这节课的内容时,主要从学生思维的矛盾、体验、理解和应用中展开关联构建,创设生态化课堂情境,形成数学学科核心素养。在探索“平行线的性质”过程中,由于学生已经掌握了同位角、内错角、同旁内角和直线平行的条件等内容,因此教师借助学习旧知展开对应探索,在教学导入、目标设定、教学突破、训练设计等多个环节展开梳理,促使学生顺利进入平行线的性质探究之中。
一、在矛盾中构建,创设生态课堂情境
“平行线的性质”涉及同位角等因素,教师应结合学生的生活经历导入新课,能够促使学生自然进入关联思考环节。
教学片段1:创设情节,导入新课
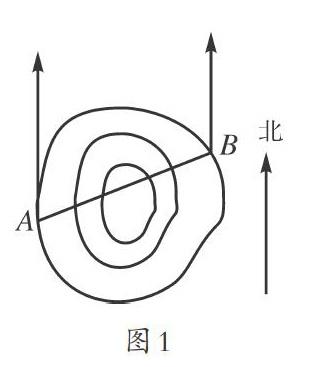
教师先引导学生回顾平行线的判定定理,然后利用多媒体投放地形图案例。(如图1所示)
观看这个图例,可以找到A、B两个点,这两个点位于龙山的两端,现在要从A点开始挖掘隧道,走向是北偏东68度。如果A、B两端同时开工,B地要按什么样的方位进行施工才能准确对接呢?要解决这个问题,需要借助“平行线的性质”相关内容。学生开始思考和讨论,对相关内容进行对应研究,课堂学习气氛逐渐浓厚。
在这个片段中,教师从学生的生活实际出发,搜集学生比较熟悉的实际问题,为学生设定了学习情境。这个案例带有生活气息,能够顺利引起学生的关注,激发学生主动探究的积极性。学生在解决现实生活中的数学问题时,第一时间会想到如何运用学习旧知的方法展开对应操作,但发现旧知不能解决问题后,自然会产生一种矛盾心理,思维构建也随即打开,“平行线的性质”涉及同位角、内错角、同旁内角等多个数学因素,如何进行对应思考和构建,这是学生要直面的问题。教师利用多媒体展示图例开展助学操作,符合生态课堂构建的特点。
二、在体验中生成,打造生态课堂环境
学生进入学习环节后,要对涉及因素进行梳理和思考,形成多种体验。教师要关注学生的学习表现,及时发现问题,并做出必要的引导,能够自然形成教学动机。
教学片段2:合作交流,探究体验
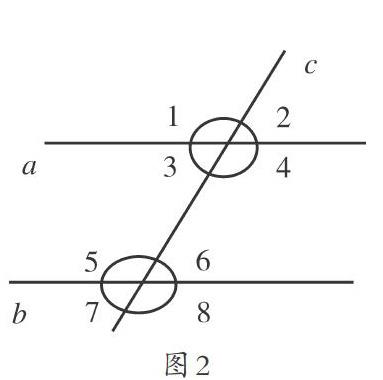
“平行线的性质”涉及两条平行线和第三条直线,三条线交叉形成同位角、内错角、同旁内角等,教师在黑板画出这个示意图(如图2),并要求学生自行操作,在白纸上画出这个图形,对图形中所有角进行测量,归纳总结自己的发现。
学生开始绘制并测量相关角的度数,教师深入到课堂之中,对学生的学习及操作情况进行观察,提示学生找出各种角的对应关系。学生找到了同位角相等、内错角相等、同旁内角互补等规律,自然生成平行线的性质的认知。
教师在课堂教学中引导学生展开实际绘图测量活动,给学生提供直接的体验机会。学生根据测量结果进行梳理,得出了一些规律性的认知,这无疑是最为可贵的操作实践。学生是学习的主体,教师围绕学生主体设计教学环节,让学生在自我发现中形成学习思考,由此建立起来的学科认知会更加深刻。
三、在理解中关联,提升生态课堂效率
课堂教学需要多重互动,教师在具体设计和组织时,要充分考虑学生的思维频度,在训练中形成反馈,能够有效提升学习效率。
教学片段3:设计反馈训练,关注思维评价
教师借助简单的图形设计展开训练设计,能够顺利调动学生的主动思维,建立师生互动。如以下几道练习题:
第一题:图3中,a、b两条线被c直线所截,得出∠1=∠2的依据应该是什么?
第二题:图4中,如果AB∥CD,那么( ).
A.∠1=∠4 B.∠1=∠3 C.∠2=∠3 D.∠1=∠5
第三题:在图5的平行四边形ABCD中,下面这些算式不一定正确的是( ).
A.∠1+∠2=180° B.∠2+∠3=180°
C.∠3+∠4=180° D.∠2+∠4=180°
这些题目的难度不大,学生通过自主思考和操作,大多能够顺利得出正确答案。第一题是考查学生平行线的性质推理的,学生都能够顺利找到“同位角相等,两直线平行”。第二题先设定了两条直线平行,通过对角的属性进行判断,自然建立同位角、内错角相等的认知。学生对这些操作不会产生更多的疑问。第三题考查的是同旁内角互补的相关内容,首先要判断两个角是不是同旁内角,就要追溯到两直线是不是平行,这样才能建立相关认知。学生在具体分析讨论中,都能够主动发言,课堂互动频繁和谐,学习构建顺利展开。
在练习设计和指导过程中,教师为学生投放适合的训练内容,成功引发学生对应的思考,并在不断推演中形成学习认知。题目都属于基础过关的范畴,学生解答问题不大,教师与学生形成互动反馈,确保训练顺利推进。
四、在应用中体验,建立生态课堂基础
平行线的性质的应用极为广泛,教师要对接学生生活认知基础开展设计,让学生在应用体验中形成理论并归纳总结。
教学片段4:组织性质归纳总结,形成认知基础
教师投放问题:“平行线有哪些性质?”学生回答:“平行线被第三条直线所截,同位角、内错角相等,同旁内角互补。”
教师再组织学生合作学习讨论:平行线的性质和直线平行的条件有什么样的关联?学生开始互动交流,课堂学习气氛浓厚。平行线的性质和直线平行的条件有诸多关联,同位角相等、内错角相等,这是平行线的性质,也是直线平行的条件,二者是相通的关系。
平行线的性质探究需要系统性训练,教师借助学生掌握舊知展开引导,利用更多生活案例和图式进行对应训练设计,将学生带入实践操作环节,并在实际操作体验中形成学习回馈。教师与学生展开多重对话交流,对平行线的性质相关认知进行归纳总结和升华,将学科教学推向深入。在这个操作过程中,教师从几个角度展开推演,形成崭新的学习动机。
首先,教师利用生活案例进行教学,给学生提供深度思考的机会。学生对生活中平行线的应用缺少对应思考,教师以此作为教学起点,将学生的数学思维引入到生活案例之中,进一步形成对应调动,获得不错的启动效果。
其次,教师借助一些图式展开具体的解读,给学生规划清晰的思考路线,让学生在具体体验中形成学科认知基础。平行线的性质是几何的重要内容,利用图式进行解读和梳理,符合学科教学的基本要求,与学生的认知达成更多的契合。
最后,教师运用训练进行巩固实践,让学生在归纳总结的基础上进入训练环节,促使学生顺利完成平行线的性质认知的构建。教师参与学生训练设计,对学生训练实际做科学评估,形成科学的指导,进而为学生顺利开展学习内化创造条件。课堂教学设计需要充分考虑多种制约因素,唯有达成更多契合,才能形成课堂构建力量。
数学生态课堂的构建,需要教师做出系统性的设计和组织,针对学生的学习体验进行教学调度,能够为课堂构建创造良好的条件。学生是学习的主体,教师在执教过程中,要关注学生的学习体验。“平行线的性质”教学本身没有太大的难度,教师从学生认知基础展开体验设计,让学生逐渐进入学习环节,自然形成学科认知基础。
作者简介:覃超胜(1977— ),广西陆川人,大学本科学历,一级教师,主要从事初中数学教学与研究。
(责编 黄健清)

