基于改进遗传算法的校园食堂外卖配送路径优化研究

王 迪，金 辉，靳泽宇，常广文

基于改进遗传算法的校园食堂外卖配送路径优化研究

王 迪，金 辉，靳泽宇，常广文

（辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001）

以辽宁工业大学校园食堂外卖配送为研究对象，建立以行驶距离最短为优化目标的外卖配送路径数学模型，采用改进的遗传算法进行求解，并利用模拟退火算法求解进行对比分析，结果证明改进遗传算法的有效性。

外卖配送；路径优化；改进遗传算法；MATLAB

随着互联网以及O2O商业模式的不断发展，人们的生活节奏不断加快，网络订餐平台得到高速发展，越来越多的人开始通过的O2O方式(即消费者通过手机、电脑等移动终端，在网络上购买商品，由商家接单后送货上门的方式)购买外卖。由于现在物流配送不能有效满足网上订餐服务的急切需求，导致外卖物流市场中第三方物流企业的进入。第三方外卖配送企业即商家将外卖配送业务外包给物流企业，商家只需要专注于餐饮服务即可，其他的一系列配送服务由这些专业的物流企业来进行，这样既节约成本，也保障了配送服务的标准化[1]。

外卖物流为“短物流运输”，随着手机网络的快速发展，手机订餐服务也快速蔓延开来，尤其是在大学校园，这种以美团、饿了么为代表的订餐APP广受在校大学生的喜爱。这种新型的用餐服务模式得到迅速发展的原因主要由以下3点：第一，学生群体的易接受性。学生是接受新奇事物最快的群体，利于新消费模式的推广。第二，高校区域的密集性。高校是各商家集中最紧密的区域之一，这样的集中性使得配送物流的管理更加的容易。第三，因为学生有固定的作息时间，校园食堂就会存在就餐高峰期，因为某些原因有些学生无法去餐厅就餐，只得借助外卖配送，节约时间，缓解就餐压力。因此做好校园外卖配送管理，不仅有利于学校安全管理，更有利于学生的学习和生活[2]。

涂汉江[3]利用TSP问题对外卖配送进行建模，使用分支限界法进行求解，从而建立一个外卖订餐系统。王帅等[4]利用旅行时间随机的VRP问题建立外卖配送模型，并使用遗传算法进行求解，提高了顾客满意度，并设计了一种配送时间随机的外卖配送方案。郭月等[5]通过研究北京物资学院的校园外卖配送情况，建立基于节约里程法校园外卖路线规划模型，改善了校园外卖配送情况。

外卖配送问题一直是一个难以解决的问题，在配送服务过程中，顾客与商家约定送达时间，一旦外卖未能及时送抵，顾客便会不满，甚至于将这些不好的信息反馈到外卖平台之上，这些信息在别的顾客进行购买时会有很大的消极作用，会损伤商家的信誉，因此，如何合理地解决外卖配送问题具有十分重要的意义[6]。

1 问题描述

为了研究辽宁工业大学校园外卖配送路径，可以将该项目描述为：在辽宁工业大学内，共有4个食堂，可以将这4个食堂看作出发点，4个食堂都要向位于学校内的各个宿舍楼以及各个教学楼和不同地点配送外卖，每个需求点在不同时间段内都有着各自的需求情况，现各个食堂选择的配送方式都默认为电动车配送，且配送车辆都存在容量限制，以行驶距离或时间最短为目标。因为校园外卖配送都在固定的时间段内，因此在满足要求的情况下，本文主要研究各食堂在中午和晚上高峰期外卖配送的最优路径。

2 数学模型的建立过程

2.1 模型假设

(1)每名送餐员都是从食堂出发进行外卖的配送，即把每个食堂点作为外卖配送的出发点即“配送中心”，并且每个食堂的位置已知，送餐员从食堂出发进行外卖配送任务，任务完成后都返回食堂。

(2)每个需求点的位置和外卖需求量均为已知的，并且保证每个配送点都会被服务到，而且每个需求点仅有1名送餐员为其提供送餐服务。

(3)每辆电动车都是有载重限制的，即送餐员在进行外卖配送时，携带的餐盒数量不能超过每辆电动车的最大载重数量。

(4)进行外卖配送的电动车由食堂统一提供，因此电动车的外形、载重能力、车型大小、电池续航能力都是相同的，其中电动车的最大行驶距离也是相同的。

(5)在固定时间段内完成外卖配送，按照辽宁工业大学校园外卖情况调查问卷显示，食堂配送基本上都在中午以及下午的固定时间，在这段时间内，基本上所有的开始送餐时间以及最晚送达时间大致相同，因此所有车辆都会在固定时间段内完成外卖配送。

2.2 数学模型

针对本文的目标，建立如下的模型。

(1)目标函数：

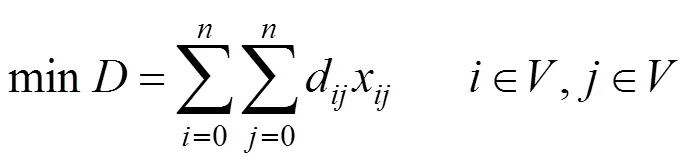
(2)决策变量：

(3)约束条件：

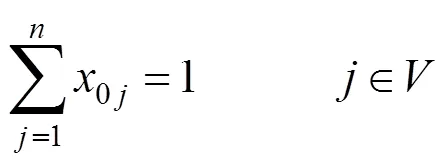
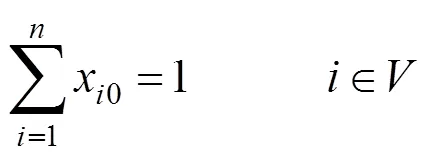
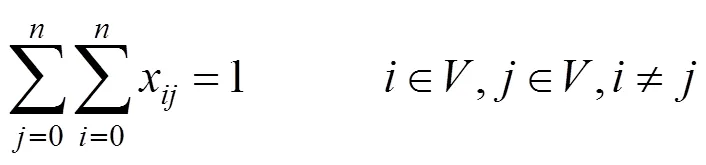
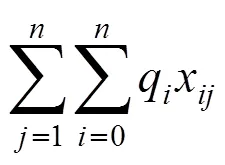
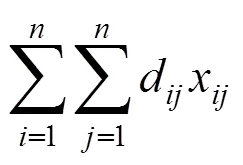
式(3)表示送餐员需要在完成任务后，返回食堂。

式(4)表示在每一次配送过程中，每一个有需求的地点都将会被服务到，每一条配送路径都会连接一个配送中心，并且从该“配送中心”出发只连接一个需求点。

式(5)表示在快递配送服务过程中，每个需求点都有1个送餐员服务，而且仅能被服务1次。

式(6)表示每次配送的送餐量不能超过配送电动车辆的最大载量限制。

式(7)表示优化路径距离不超过电动车可行驶的最大距离。

式(8)表示在每一次配送开始的时候，送餐员都是从食堂出发。

3 模型求解

3.1 改进遗传算法

(1)染色体的编码

遗传算法运算效率和运算结果绝大程度上由染色体的编码方式的好坏直接影响，因此选择合适的染色体编码方式对于遗传算法的实现是至关重要的。

由于本文的外卖配送问题只存在3个食堂点(即配送中心)和18个需求点，数目较小，因此采用较为简单自然数编码的方式对染色体进行编码，将染色体分为21段，其中每一段代表每一个需求点的编号，分别用1，2，…，21表示，其中1，2，3表示的是配送中心，即各个食堂出发点。例如，|19|5|7|9|20|11|13|1|21|3|15|4|8|12|2|6|10|14|17|18|16|就是一条染色体。

(2)初始群体的选取

在遗传算法的求解过程中，初始种群的个体一般是通过随机选取产生的。因此在本文中也采取随机的策略来生成初始种群，首先根据外卖配送的范围，确定大致初始解的空间范围，根据最优个体在空间内的分布，以此选择初始种群范围。

因为根据辽宁工业大学校园外卖配送需求情况，本文共调查选取21个点，3个食堂出发点即“配送中心”，18个需求点，故本文将初始种群的数值设置为100。

(3)适应度函数的选择

适应度函数值的大小代表的是染色体优劣程度的标准，根据“优胜劣汰，适者生存”的标准，适应度函数值越大的染色体就说明它适应环境的能力越强，表明其越优质，反之则越劣质。由于外卖配送的目标函数追求的是行驶距离最短，因此本文利用目标函数D(=1，2，3)的倒数表示种群个体的适应度函数。当总的配送行驶距离越小即目标函数值越小时，适应度函数值也就越大，表明其适应性越好，也就是被遗传到下一代的概率也就越大。

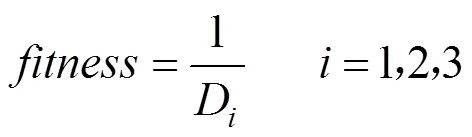
(4)选择操作

种群个体的选择是建立在种群个体的适应度评估的基础上的[6]。随机遍历抽样法、局部选择法、适应度占比选择策略、轮盘赌选择法等方法是遗传算法中常用的选择操作方法。本文采用的则是轮盘赌选择法，具体操作步骤如下所示。

①由初始种群个体的适应函数值(x)，将每个个体的适应度值相加得到总的适应度值D，公式如下：

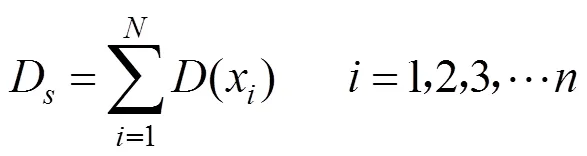
②在[0，s]之间随机产生一个数值；

③然后第一个开始，把每个个体的适应度数值进行相加，当相加数值的大小超过s时，则最后一个累加的个体将作为被选中的个体。

(5)交叉操作

交叉操作是根据交叉率将两个父代个体之间染色体上的基因进行交叉互换，从而产生新的染色体个体的操作。染色体的交叉方法主要有单点交叉、两点交叉、多点交叉等形式。本文采用的是适用自然数编码的单点交叉法，具体操作是首先在个体串中随机生成一个交叉点，在交叉过程中，将这两个个体在交叉点前后的两部分结构进行交叉互换，从而生成两个新个体。若一个染色体的编码长度，则共有-1个可供选择的交叉点[6]。如下面所示，演示了染色体中基因进行交叉变异产生的流程示意过程。

①父代个体染色体的基因排列方式：

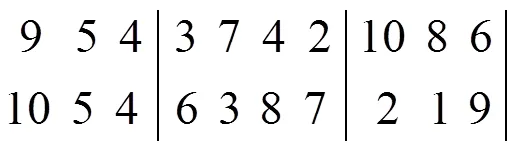
②当满足交叉概率时进行交叉变异：

③子代的交叉变异结果为：

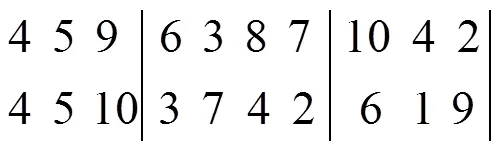
(6)变异操作

遗传变异指的是某些个体的染色体中的某个或几个位置的基因发生突变，转变为其他的同等位置基因，最后生成新的变异个体。变异能够提高种群个体的多样性，使遗传算法具有局部搜索能力，防止算法过早收敛。传统的变异算子有边界变异、均匀变异、高斯变异等。本文根据自然数编码的特点，设计如下所示的变异操作步骤。

①在（0，1）之间产生一个随机数；

②判断随机数与m的大小；

③如果<=m，则随机产生两个基因突变位；

④将这两个基因突变位上的基因进行交换。

例如开始时的基因位置为：

9 5 1 ¦ 6 ¦ 3 8 ¦ 7 ¦ 10 4 2

变异后的基因位置为：

9 5 1 ¦ 7 ¦ 3 8 ¦ 6 ¦ 10 4 2

图1所示为改进遗传算法求解外卖配送路径问题时的基本流程图。

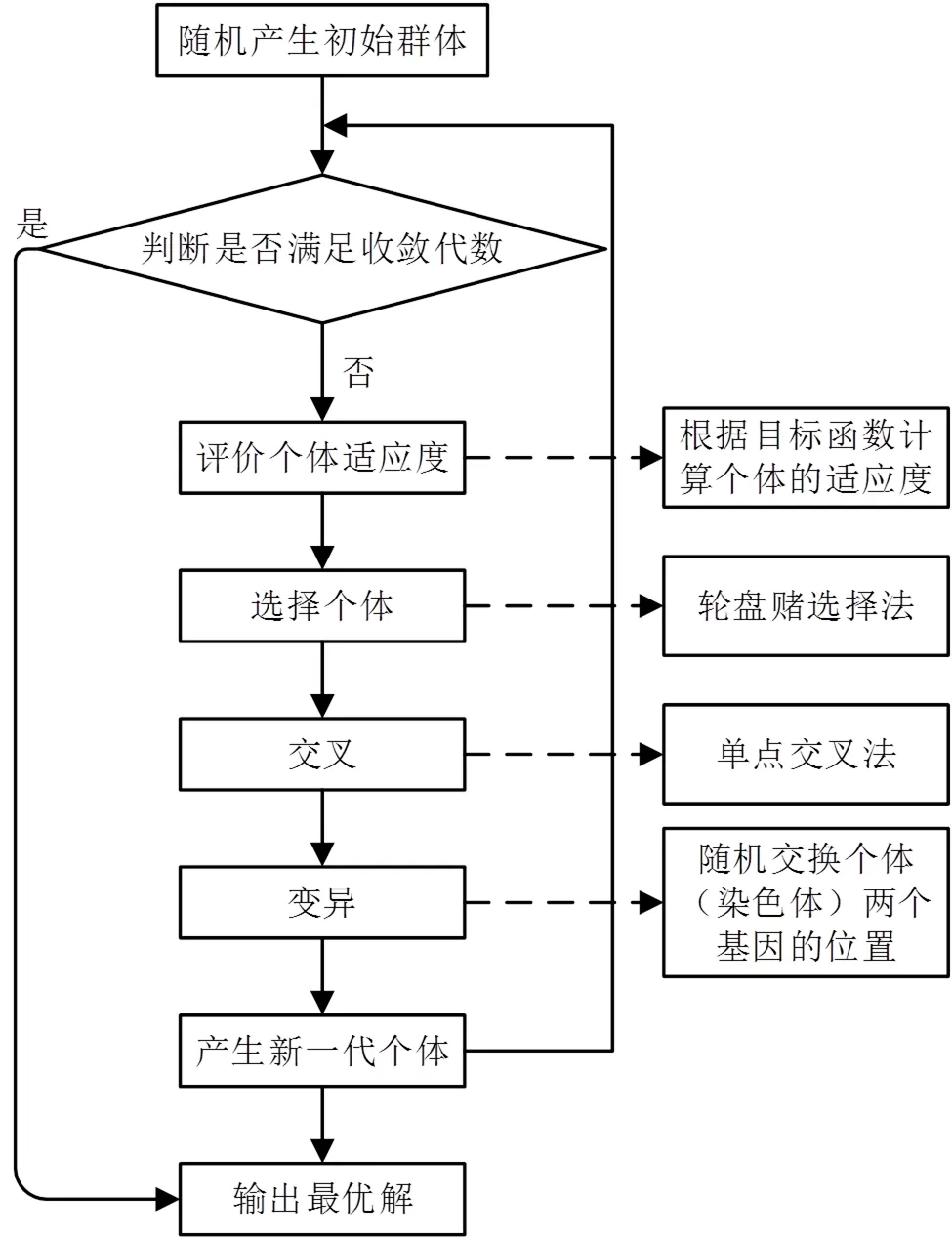
图1 算法流程图

3.2 实例

辽宁工业大学校园共有4个食堂(其中南区2个，北区2个)，由于南区的2个食堂(一、二食堂)建立在一起，故这里以1个配送中心来计算，以下统称为南区一二食堂，北区2个食堂距离较远，故以2个配送中心来分别计算，分别为北区三食堂、北区四食堂。

如图2所示，利用百度地图标记的各食堂的具体位置以及校园内各个需求点位置。

3.2.1 数据处理

(1)得到调查的原始数据后，根据地址在百度地图中查找出其经纬度。例如图中标记的“南区一二食堂”，在百度地图中查找该点，得到的经纬度坐标为(121.130563，41.147333)。表1所示为各个标记点的经纬度坐标。

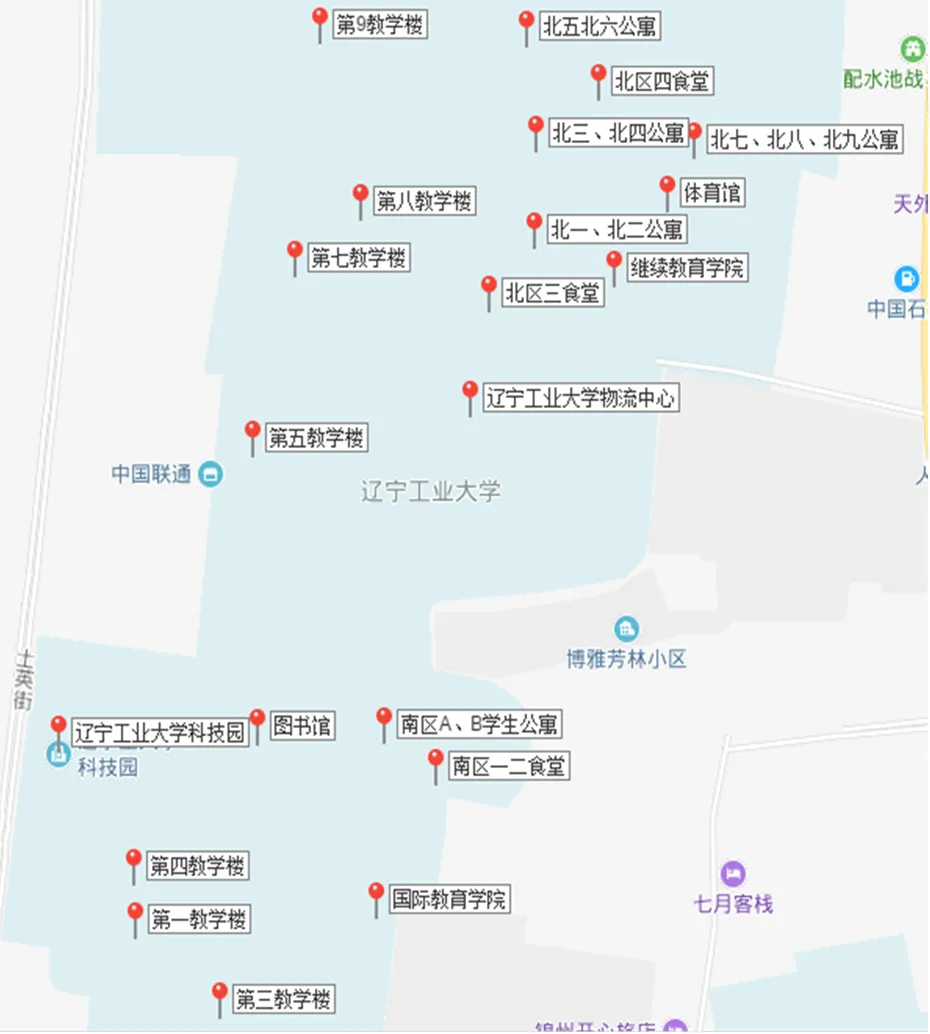
图2 各点百度地图分布图

表1 各点经纬度表

(2)利用Excel软件进行高斯投影换算，将经纬度坐标换算到高斯平面直角坐标。例如编号为1的“南区一二食堂”经纬度坐标为(121.130563，41.147333)，换算之后得到的平面直角坐标为(4568831.498，5718.080486)。因为本文所研究范围在辽宁工业大学校区内，所有编号点的经纬度坐标的差异值很小，经过换算得到的平面直角坐标值的差异主要从千位开始，因此为了方便计算，将坐标值进行处理后得到(8831，5718)。表2所示为各点处理后的平面直角坐标。

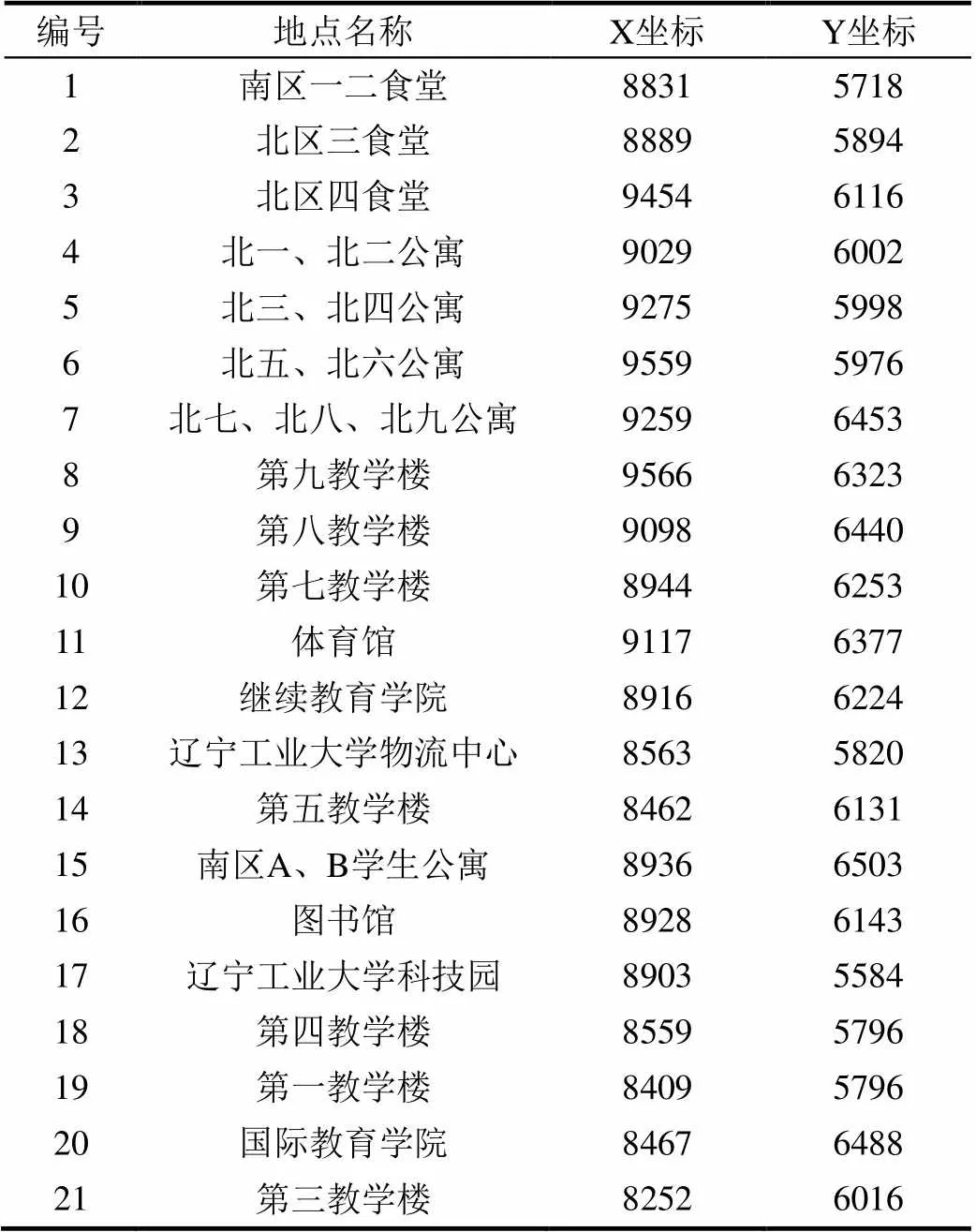
表2 各点平面直角坐标

(3)建立坐标系，并用MATLAB绘制散点图，如图3所示。

图3 各点分布散点图

3.2.2 仿真模拟及结果分析

根据实际情况设定参数值，交叉和变异概率分别为c=0.7%、m=0.06%，迭代次数为200。通过MATLAB进行程序仿真模拟，得到配送路径轨迹图。并利用模拟退火算法求解各个食堂到各个需求点(寝室楼、教学楼等)的最短路径，通过两者之间的比较，直观看出改进遗传算法的求解效果和收敛性。

如图4所示，为改进遗传算法和模拟退火算法求解的以一二食堂为出发点的最优配送路径图，图5为其迭代次数。

由运行结果可知改进遗传算法求得的最优解：3→8→10→14→2→15→1→11→16→17→19→12→18→1→7→9→5→6→4→3；总距离4 465 m。

模拟退化算法求得的最优解：11→1→15→2→14→10→8→9→3→4→6→5→7→13→18→12→19→17→16→11；总距离：4 605 m(此时“1”表示的为出发点，即“一二食堂”坐标点位置)。

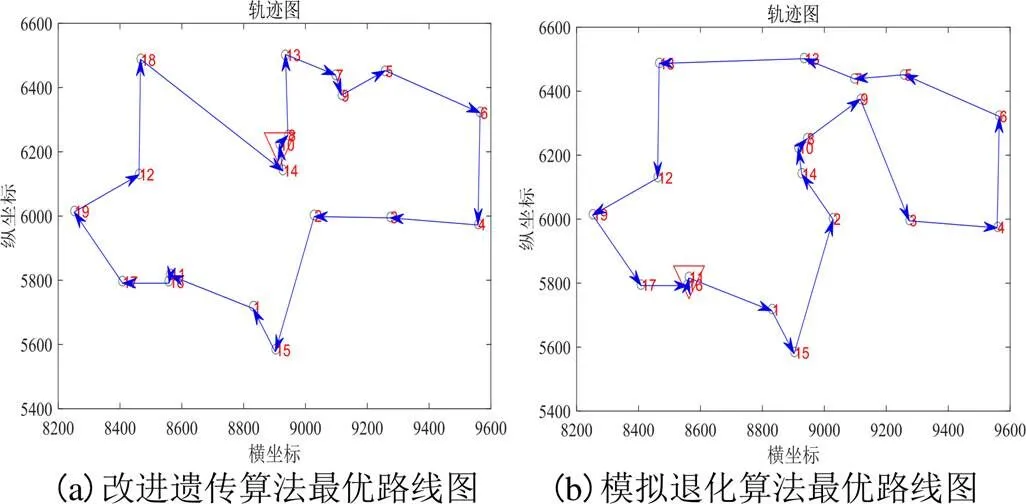
图4 一二食堂到各点的最优配送路径图

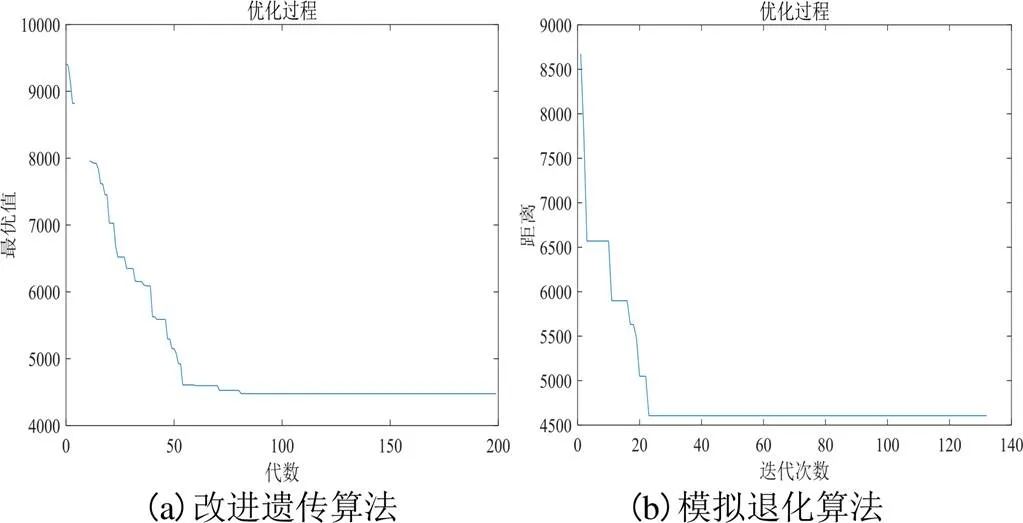
图5 迭代次数对比图

图6所示为三食堂为出发点的最优配送路径图，图7为其迭代次数。

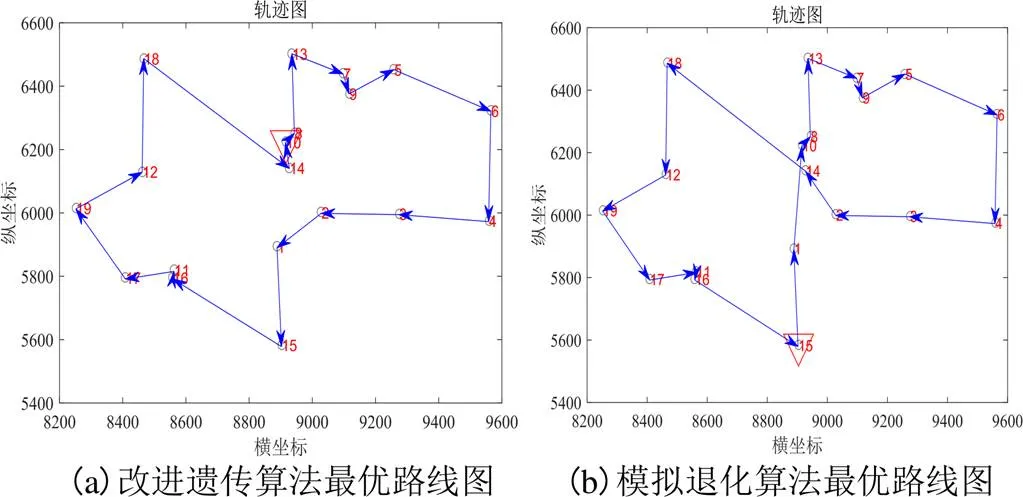
图6 南区三食堂到各点的最优配送路径图

图7 迭代次数对比图

由运行结果可知改进遗传算法求得的最优解：5→6→4→3→2→1→15→16→11→17→19→12→18→14→10→8→13→7→9→5；总距离：4 498 m。

模拟退化算法求得的最优解：15→1→10→8→13→7→9→5→6→4→3→2→14→18→12→19→17→11→16→15；总距离：4 744 m(此时“1”表示的为出发点，即“三食堂”坐标点位置)。

图8所示为四食堂为出发点的最优配送路径图，图9为其迭代次数。

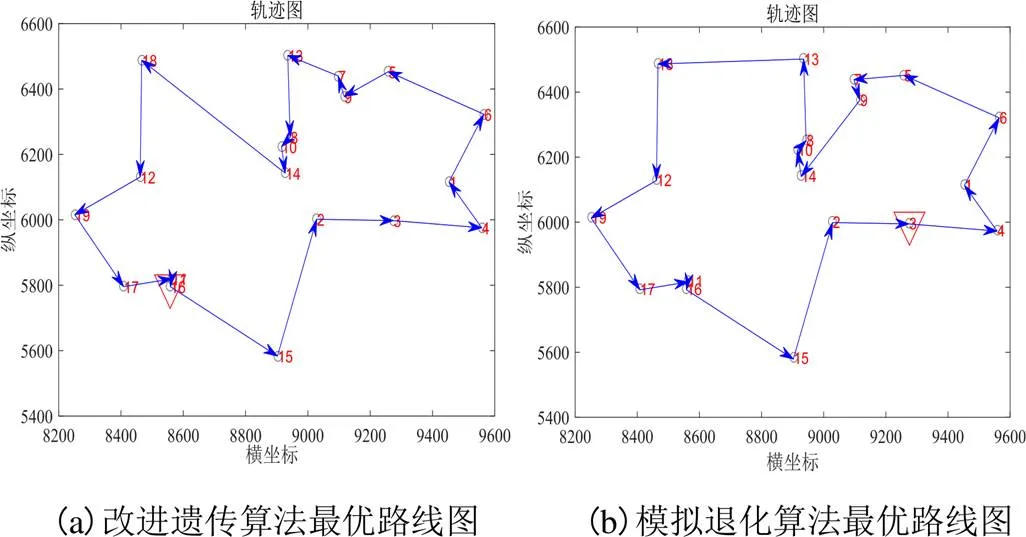
图8 南区三食堂到各点的最优配送路径图

图9 迭代次数对比图

由运行结果可知改进遗传算法求得的最优解：16→15→2→3→4→1→6→5→9→7→13→8→10→14→18→12→19→17→11→16；总距离：4 511 m。

模拟退化算法求得的最优解：3→4→1→6→5→7→9→14→10→8→13→18→12→19→17→11→16→15→2→3；总距离：4 531 m(此时“1”表示的为出发点，即“四食堂”坐标点位置)。

通过以上对比结果分析可以发现，改进的遗传算法求解最优配送路径距离比模拟退火算法求得的距离更优些，但前者收敛速度较慢，迭代时间较长，后者收敛速度较快，因此对于求解较大规模的优化问题时，此改进方法还不能有效满足求解要求，因此需要继续改进。

4 结论

通过本文的研究，优化了辽宁工业大学校园食堂外卖配送路径，在中午以及下午就餐高峰期间可以大大地减少配送成本，缩短配送时间，提高商家的收益。

(1)该配送方法减少了配送距离。相比于以往的人工配送，不同配送人员在配送的过程中会选择不同的下一个配送节点，导致了部分不熟悉的配送人员在校园内绕远，或者在校园内来回往返，通过该方案可以减少不必要的路程，缩减配送距离，提高效率。

(2)该配送方法减少了客户的等待时间。配送效率的提高就意味着顾客等待时间的减少，同时也意味着客户满意度的提高，配送人员可以在短时间内完成配送，大大提高了客户的好感，如果这种好的反馈到市场当中，会导致越来越多的人接受并使用这种消费方式，尤其是这些反馈较好的商家，会提高很大的收益，同时推动整个市场的发展。

[1] 翟劲松, 台玉红. 基于时间窗约束下的外卖配送路径优化[J]. 物流科技, 2018, 41(3): 15-18.

[2] 徐镇邦, 裴兵. 网络订餐服务的物流配送系统探析[J]. 商场现代化, 2014(22): 74-75.

[3] 涂汉江. 集中区域外卖即时配送调度系统的设计实现[D]. 南昌: 南昌大学, 2016.

[4] 王帅, 赵来军, 胡青蜜. 随机旅行时间的外卖O2O配送车辆路径问题[J]. 物流科技, 2017, 40(1): 93-101.

[5] 郭月, 张涵. 校园外卖配送体系研究[J]. 中国市场, 2016(20): 67-69.

[6] 许刚. 基于广义多子代遗传算法的外卖配送问题研究[D]. 哈尔滨: 东北农业大学, 2017.

Research on Optimization of Delivery Path of Campus Canteen Delivery Based on Improved Genetic Algorithm

WANG Di, JIN Hui, JIN Ze-yu, CHANG Guang-wen

（School of Automotive and Traffic Engineering, Liaoning University of Technology, Jinzhou 121001, China）

This paper takes the delivery of the canteen in the campus of Liaoning University of Technology as the research object, and establishes the mathematical model of the take-away delivery path with the shortest driving distance as the optimization target. The improved genetic algorithm is used to solve the problem, and the simulated annealing algorithm is used to solve the comparative analysis. The result proves that the improved genetics the effectiveness of the algorithm.

takeaway distribution; path optimization; improved genetic algorithm; MATLAB

U116.2

A

1674-3261(2019)01-0047-06

10.15916/j.issn1674-3261.2019.01.011

2019-07-17

辽宁省教育厅重大科技平台科技项目(JP2017009)

王迪(1994-)，男，河南南阳人，硕士生。

金辉(1963-)，女(满族)，辽宁锦州人，教授，博士。

优先出版地址：http://kns.cnki.net/kcms/detail/21.1567.T.20191227.1019.008.html

责任编校：孙 林