基于熵权-直觉三角模糊数物流服务商的选择决策研究
徐登科,欧阳璐
基于熵权-直觉三角模糊数物流服务商的选择决策研究
徐登科,欧阳璐
(湖南工业大学 商学院,湖南 株洲 412007)
利用直觉三角模糊数,结合熵权法,通过集结各位专家决策矩阵,计算备选物流服务商各评价属性的综合评价值,再计算各计分函数值和精确函数值比较其大小,得出备选物流服务商评价值大小排序,即得到各物流服务商的综合选择决策排序。
物流服务商;熵值权重;直觉三角模糊数;选择决策
在物流服务供应链中,对功能型物流服务商的选择决策是物流集成商所要重视的一个问题,对物流服务供应链整条链的效益也有着重大影响。田宇结合运用层次分析法和线性规划的方法,构建了基于服务价格、服务质量和顾客服务这三个指标因素的物流服务商竞争力分析的指标体系,研究探讨了多源供应商选择以及最优采购量分配的问题[1]。Desheng Wu采用了决策树、数据包络分析方法、神经网络法相结合的方法来解决复杂多目标的供应商选择问题[2]。A.Azadh等也应用了数据包络分析方法、模糊理论法相结合来解决供应商选择问题[3]。王君等选取发展能力、服务能力和合作能力三大指标,以FHAP方法构建物流服务供应链的绿色供应商评价体系对供应商进行评价与选择[4]。陈可嘉种新的解决多属性决策问题的方法—基于组合权重确定的 GI-TOPSIS 方法,将灰色关联引入传统的理想解法TOPSIS中,并以企业为实例证明该方法对物流供应商选择的可行性[5]。茅盈盈将层次分析法和熵权系数法相结合运用到物流服务商的选择决策中,具有一定的现实意义[6]。Y.Chen和B.L提出了基于三角模糊数的动态多属性决策模型,为物流服务商的选择提供了新的方法[7]。魏倩采用DEA和模糊综合评价相结合的方法为供应链上游外包企业选择第三方物流服务商,用于定量分析的DEA和用于定性分析的模糊综合评价相结合的方法,构建了基于DEA的模糊综合评价与选择模型,具有实用性[8]。将定量分析和定性分析充分结合,并以实例证明该方法的优越性。Wan S.P等将物流服务商的选择作为一种典型的模糊偏好关系的群体决策问题,提出了包括乐观和悲观及混合方法在内的三种方法用于分析和构建直觉模糊线性规划模型并进行分析求解[9]。
层次分析法(AHP)定性偏好占比较大,所以主观影响因素对整个决策起着较为重要的作用,所以运用AHP分析决策方案往往存在着较强的人为偏好因素,通过AHP得出的最终决策能够反应认为的决策偏好,但基于客观事实却存在着较大的差异性。数据包络分析方法(DEA)主要是根据企业多项投入指标和多项产出指标,通过线性规划的方式,对具有可比性的同类型企业进行相对有效性评价的一种数量分析方法。DEA通过分析供应商各项指标的投入和产出效率从而选择出适合企业的供应商,此方法是定量分析方法,但是只是针对供应商的投入产出效率问题,在比较过程中,效率为100%的一些供应商被称为相对有效率供应商,而其它效率评分低于100%的供应商被称为无效率供应商。对供应商的选择具有较强武断性,每个企业的核心能力有所不同,所以其不同指标的投入产出效率也会有所不同。对于复杂的供应商选择问题,DEA并不能较为全面的反映企业对供应商的需求。
对于功能型物流服务商的选择,将考虑因素运用模糊分析方法,可以使定性和定量属性都能够有直观的呈现,再结合熵权法,能够较大程度的保留原始数据,尽量消除各指标权重的主观性,使得专家打分更具客观性。本文在综合参考其他学者文献成果下,运用直觉三角模糊数对物流服务商进行选择决策。
1 熵权-直觉三角模糊数算法
直觉三角模糊数的属性权重之一是通过专家打分的方式进行决定的,但这种方法在实际问题中存在主观性较强的问题,因此需要对专家打分的权重进行客观的分析,尽可能减少主观性的分析。本文引入熵权法到直觉三角模糊数中,通过多种指标属性评价值的变异程度来决定决策问题的属性权重,这样能够避免主管因素而带来的不良影响。
1.1 熵权法
熵权法是一种客观赋权方法。若指标的熵越小,该指标提供的信息量越小,在综合评价中所起作用理当越小,权重就应该越低[6]。因此,可利用熵这个工具,计算出各个指标的权重,为多指标综合评价提供依据。
1.2 直觉三角模糊数定义
1.2.1 三角模糊数
设、分别为模糊数的上限和下限,可能为可能性最大的值,当=(),0,称为三角模糊数,其隶度函数表示为
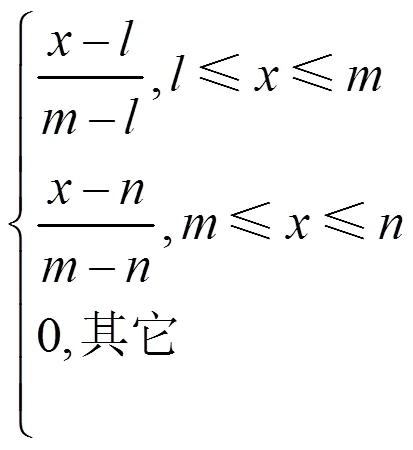
1.2.2 直觉三角模糊数
当直觉梯形模糊数=(〈,,〉;μ,ν)中=时,直觉梯形模糊数退化为直觉三角模糊数=(〈,,〉;μ,ν),隶度函数
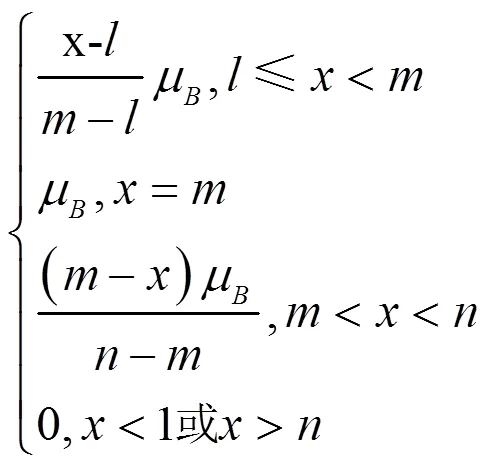
非隶度函数
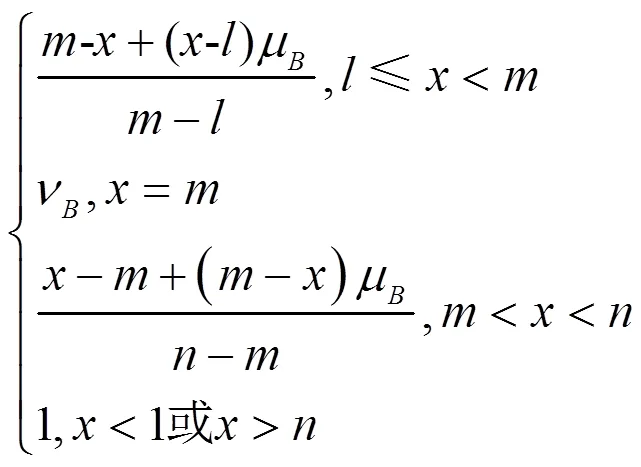
1.2 直觉三角模糊数运算及比较
设两组直觉三角模糊数分别为
1=(〈1,1,1〉;μ1,ν1),
2=(〈2,2,2〉;μ2,ν2)
则
(1)1和2的相关运算规则如下:
1+2=[(〈12,12,12〉;
min(μ1,μ2),max(1,ν2)];
1-2=[(〈12,12,12〉;
min(μ1,μ2),max(ν1,ν2)];
*1=(〈1,1,1〉;μ1,ν1)。
(2)直觉三角模糊数C=(〈〉;μ,ν),则有
计分函数为:()=[(l+2)/4]*(μ-ν);
精确函数为:()=[(l+2)/4]*(μ+ν)。
对于两组直觉三角模糊数1和2,其大小比较原则[10]为:
当(1)<(2),则直觉三角模糊数1<2;当(1)=(2),则考虑(1)和(2),若(1)<(2),则直觉三角模糊数1<2,反之,则直觉三角模糊数1>2。
直觉三角模糊数算法结合熵权法,能够较大程度的保留原始数据,尽量消除各指标权重的主观性,使得专家打分更具客观性。
2 物流服务商的选择决策
2.1 问题描述
设供选择服务商为G(=1,2,3…m),对服务商的评价属性为X(=1,2,3…),各评价属性值为Z,专家对h(=1,2,3…l)评价属性的评价值以直觉三角模糊数=(〈a,b,c〉;μ,ν)表示。
2.2 决策过程
2.2.1 熵权确定
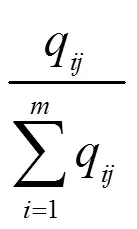
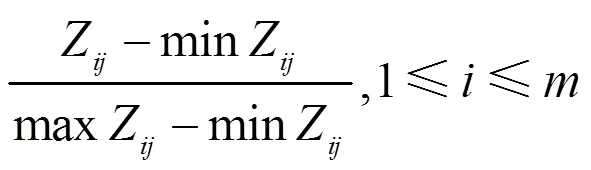
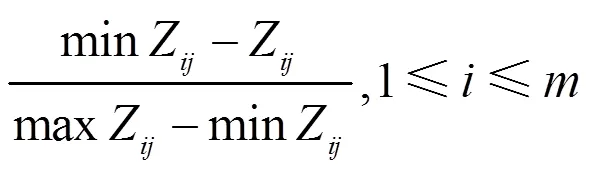
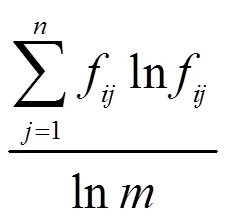

2.2.2 直觉三角模糊数综合排序
步骤一:通过专家打分和统计语言变量等方法得到直觉三角模糊数=(〈a,b,c〉;μ,ν),构造矩阵*=()*n,并规范化矩阵,得到R*=(R)*n=(〈r,s,t〉;μ,ν),且规范化分为效益型评价属性和成本型评价属性:
效益型评价属性规范化公式[11]:
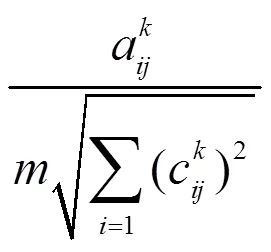
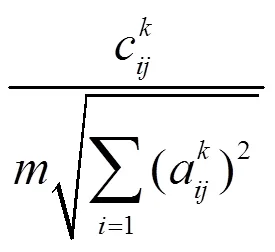
成本型评价属性规范化公式[11]:

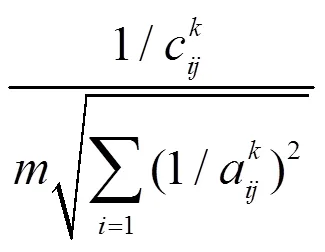
步骤二:利用TIFWA算子对决策矩阵进行集结[10-12],得到矩阵*=()*n。
设A=(〈a,b,c〉;μ,ν)为一组直觉三角模糊数,
TIFWA∶Ω→Ω,TIFWA(1,2,3…A) =
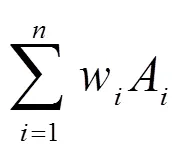
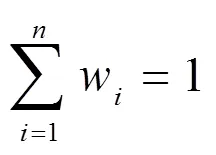
步骤三:结合各属性权重计算服务商以直觉三角模糊数表示的综合评价值。
步骤四:根据步骤三中服务商的综合评价值,比较其大小进行排序。
3 算例分析
3.1 问题描述
假设一物流集成商在选择功能型物流服务商时,以物流成本、服务质量和顾客满意度(X,=1,2,3)为主要考虑因素,且调查得到服务商的各属性值如表1所示;现邀请3位专家h(专家权重w=(0.3,0.4,0.3))对现有的4家物流商(g,=1,2,3,4)进行打分,分别如表2~表4所示。
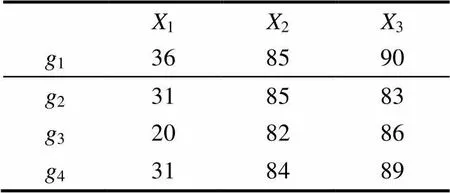
表1 服务商属性值
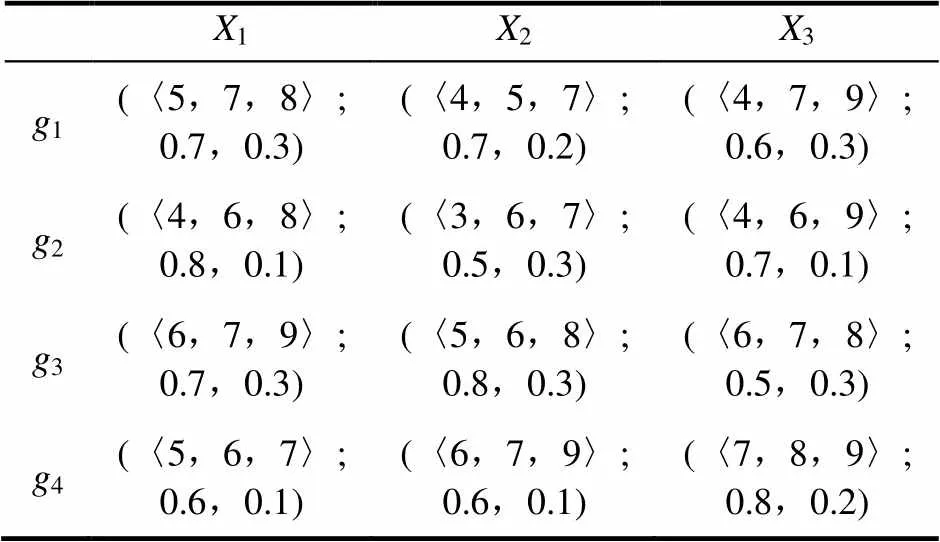
表2 决策矩阵A1
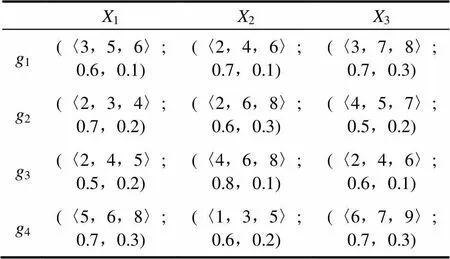
表3 决策矩阵A2
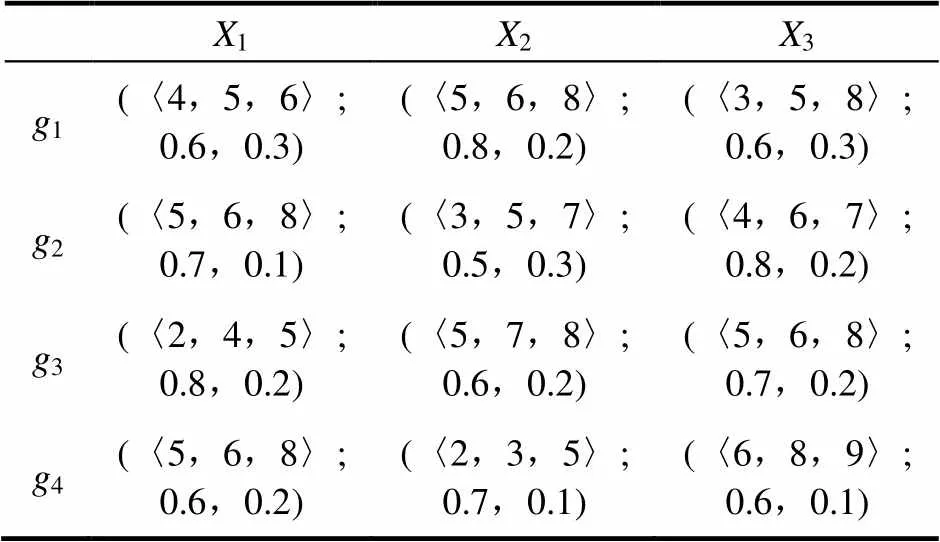
表4 决策矩阵A3
3.2 决策过程
3.2.1 熵权计算
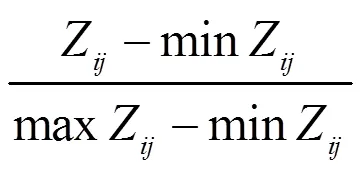
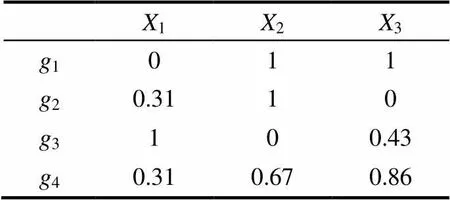
X1X2X3 g1011 g20.3110 g3100.43 g40.310.670.86
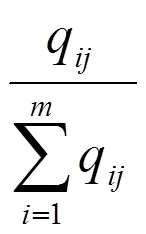
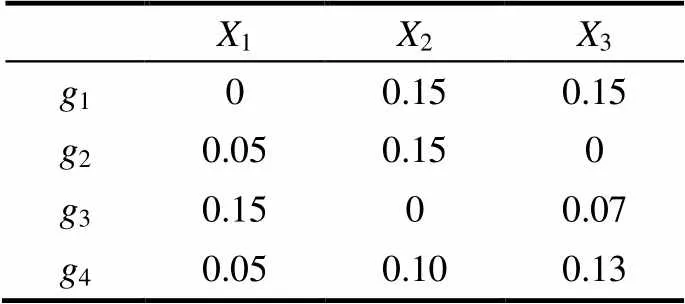
X1X2X3 g100.150.15 g20.050.150 g30.1500.07 g40.050.100.13
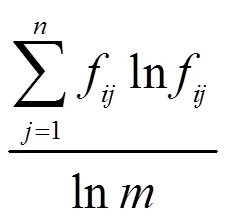

3.2.2 直觉三角模糊数综合排序
(1)1为成本型评价属性,2和3位效益型评价属性,对1、2和3进行规范化处理,得到规范矩阵
规范矩阵1
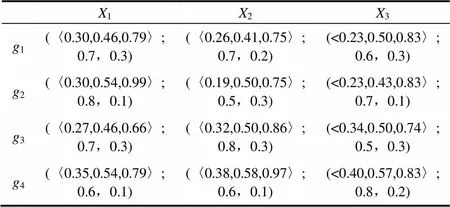
X1X2X3 g1(〈0.30,0.46,0.79〉;0.7,0.3)(〈0.26,0.41,0.75〉;0.7,0.2)(<0.23,0.50,0.83〉;0.6,0.3) g2(〈0.30,0.54,0.99〉;0.8,0.1)(〈0.19,0.50,0.75〉;0.5,0.3)(<0.23,0.43,0.83〉;0.7,0.1) g3(〈0.27,0.46,0.66〉;0.7,0.3)(〈0.32,0.50,0.86〉;0.8,0.3)(<0.34,0.50,0.74〉;0.5,0.3) g4(〈0.35,0.54,0.79〉;0.6,0.1)(〈0.38,0.58,0.97〉;0.6,0.1)(<0.40,0.57,0.83〉;0.8,0.2)
规范矩阵2
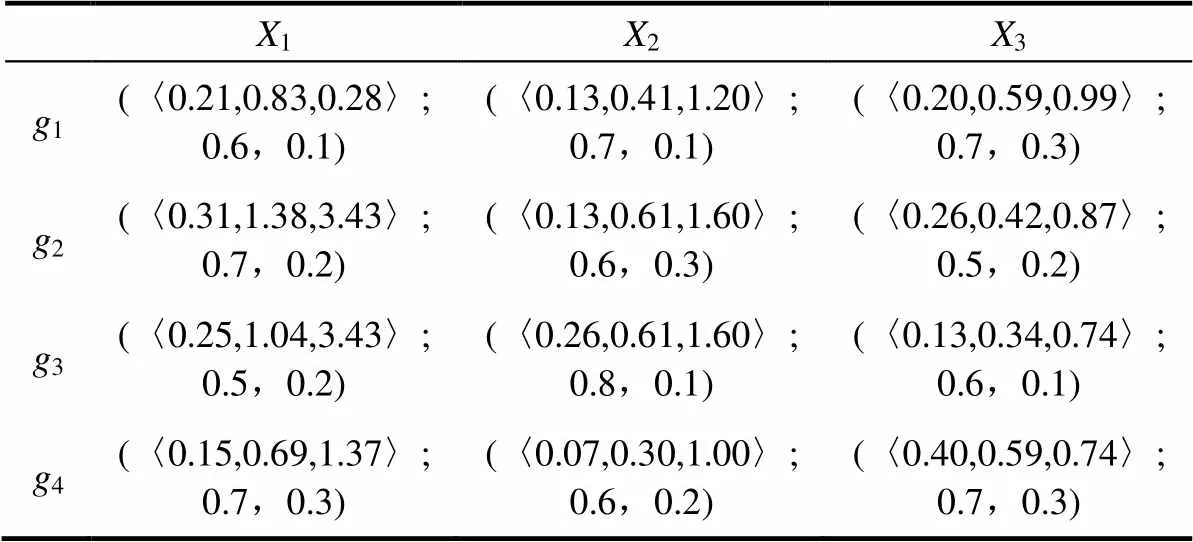
X1X2X3 g1(〈0.21,0.83,0.28〉;0.6,0.1)(〈0.13,0.41,1.20〉;0.7,0.1)(〈0.20,0.59,0.99〉;0.7,0.3) g2(〈0.31,1.38,3.43〉;0.7,0.2)(〈0.13,0.61,1.60〉;0.6,0.3)(〈0.26,0.42,0.87〉;0.5,0.2) g3(〈0.25,1.04,3.43〉;0.5,0.2)(〈0.26,0.61,1.60〉;0.8,0.1)(〈0.13,0.34,0.74〉;0.6,0.1) g4(〈0.15,0.69,1.37〉;0.7,0.3)(〈0.07,0.30,1.00〉;0.6,0.2)(〈0.40,0.59,0.74〉;0.7,0.3)
规范矩阵3
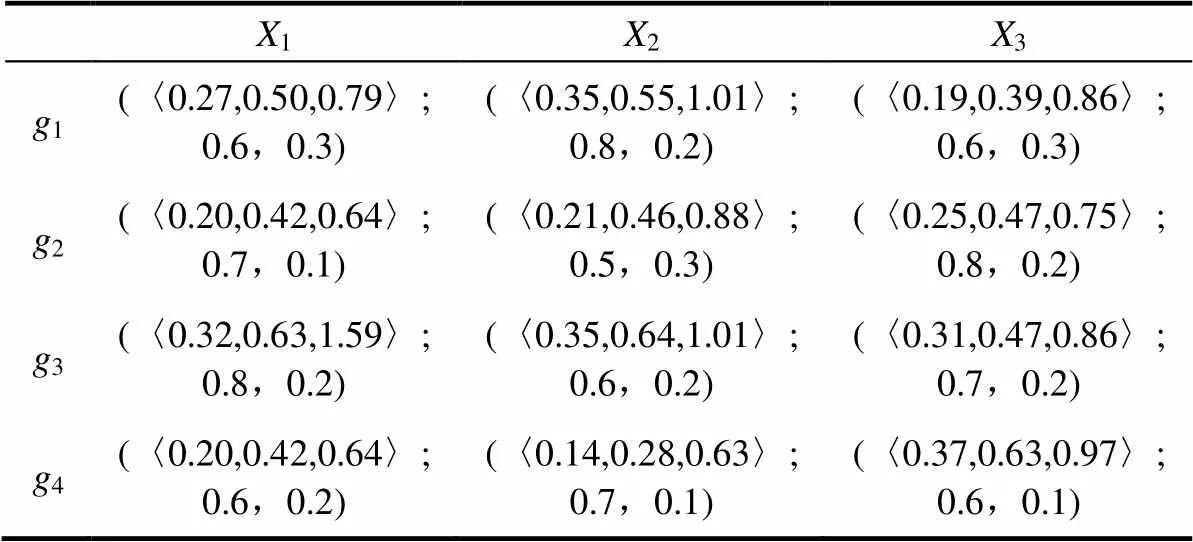
X1X2X3 g1(〈0.27,0.50,0.79〉;0.6,0.3)(〈0.35,0.55,1.01〉;0.8,0.2)(〈0.19,0.39,0.86〉;0.6,0.3) g2(〈0.20,0.42,0.64〉;0.7,0.1)(〈0.21,0.46,0.88〉;0.5,0.3)(〈0.25,0.47,0.75〉;0.8,0.2) g3(〈0.32,0.63,1.59〉;0.8,0.2)(〈0.35,0.64,1.01〉;0.6,0.2)(〈0.31,0.47,0.86〉;0.7,0.2) g4(〈0.20,0.42,0.64〉;0.6,0.2)(〈0.14,0.28,0.63〉;0.7,0.1)(〈0.37,0.63,0.97〉;0.6,0.1)
(2)利用TIFWA算子对决策矩阵进行集结,得到如下决策矩阵:
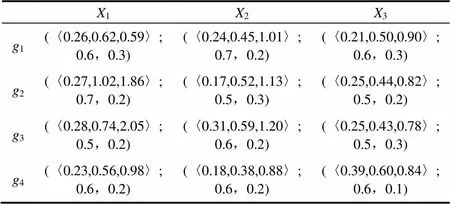
X1X2X3 g1(〈0.26,0.62,0.59〉;0.6,0.3)(〈0.24,0.45,1.01〉;0.7,0.2)(〈0.21,0.50,0.90〉;0.6,0.3) g2(〈0.27,1.02,1.86〉;0.7,0.2)(〈0.17,0.52,1.13〉;0.5,0.3)(〈0.25,0.44,0.82〉;0.5,0.2) g3(〈0.28,0.74,2.05〉;0.5,0.2)(〈0.31,0.59,1.20〉;0.6,0.2)(〈0.25,0.43,0.78〉;0.5,0.3) g4(〈0.23,0.56,0.98〉;0.6,0.2)(〈0.18,0.38,0.88〉;0.6,0.2)(〈0.39,0.60,0.84〉;0.6,0.1)
(3)由属性权重及TIFWA算子得到各服务商综合评价值G=(〈,u,ū〉;μ,ν):
1=(〈0.24, 0.53, 0.81〉; 0.6, 0.3)
2=(〈0.24, 0.70, 1.32〉; 0.5, 0.3)
3=(〈0.28, 0.60, 1.41〉; 0.5, 0.2)
4=(〈0.27, 0.50, 0.91〉; 0.6, 0.2)
(4)分别计算1、2、3和4的计分函数和精确函数:
(1)=[( 0.24+2*0.53+0.81)/4]*(0.6-0.3)=0.158
(1)= [( 0.24+2*0.55+0.78)/4]*(0.6+0.3)=0.475
同理可得
(2)=0.148,(2)=0.592;(3)=0.217,(3)=0.506;(4)=0.218,(4)=0.436
通过比较,得到(4)>(3)>(1)>(2),则有4>3>1>2,即物流服务商1、2、3和4的综合排序为4>3>1>2。
4 结论
上述计算决策过程是综合运用主客观因素进行的,得出结果也更具可信度。而倘若利用AHP进行分析决策,其过程和结果会存在着较强的主观性,AHP分析方法中,对于评价属性的权重赋予是人为的偏好决定的,在这样的分析基础上,会对判断矩阵中的决策结果产生较大的影响,使其最终决策结果社会客观性较弱,且由于AHP需要对各个指标两两对比,其计算也较为繁杂,若是指标过多其计算的结果难免会有所误差。
物流服务商的选择决策关系着物流集成商的效益,对整条物流服务供应链的发展也是非常重要的一环。利用熵权-直觉三角模糊数对物流服务商进行选择决策,对定量和定性属性可以结合计算,也考虑到了物流集成商对各属性的偏好和各位专家的权重信息,整体过程比较客观,有效地提高了选择决策的合理性和有效性。
[1] 田宇. 物流服务供应链构建中的供应商选择研究[J]. 系统工程理论与实践, 2003, 5: 49-53.
[2] Wu Desheng. Supplier selection: A Hybrid Model using DEA, Decision Tree and Neural Network[J]. Expert Systems with Applications, 2009, 36(5): 9105-9112.
[3] Azadeh A, Alem S M. A flexible deterministic, stochastic and fuzzy data envelopment analysis approach for supply chain risk and vendor selection Problem: Simulation analysis[J]. Expert Systems with Applications, 2010, 37(12): 7438-7448.
[4] 王君, 刘凡, 张志勇. 基于FAHP的物流服务供应链绿色供应商选择研究[J].安徽农业科学, 2014, 42(18): 5997-6000, 6017.
[5] 陈可嘉. GI-TOPSIS方法在逆向物流供应商选择中的应用[J]. 中国流通经济, 2014, 28(3): 39-48.
[6] 茅盈盈. HY 公司物流供应商的选择与评估[D]. 上海: 华东理工大学, 2011.
[7] Chen Y, Li B. Dynamic multi-attribute decision making model based on tri-angular intuitionistic fuzzy numbers[J]. Scientia Iranica, 2011, 18(2): 268-274.
[8] 魏倩. 基于DEA与模糊综合评判的第三方物流服务商评价研究[J].中小企业管理与科技: 下旬刊, 2012(4): 215-216.
[9] Wan Shu-Ping, Wang Feng, Lin Li-Lian, et al. An intuitionistic fuzzy linear programming method for logistics outsourcing provider selection[J]. Knowledge-based systems, 2015, 82(JuL.): 80-94.
[10] 聂荣荣. 基于直觉三角模糊数的多准则决策方法研究[D]. 长沙: 中南大学, 2010.
[11] 范荣华. 基于直觉模糊数的物流配送中心选址的评价方法[J]. 统计与决策, 2016(23): 33-36.
[12] 万树平, 董九英. 基于三角直觉模糊数Choquet积分算子的多属性决策方法[J]. 中国管理科学, 2014, 22(3): 121-129.
[13] Li D F, Nan J X, Zhang M J. A Ranking Method of Triangular Intuitionistic Fuzzy and Numbers Application to Decision Making[J]. International Journal of Computational Intelligence Systems, 2010, 3(5): 522-530.
Research on Selection Decision of Logistics Service Provider Based on Entropy Weight-intuition Triangular Fuzzy Number
XU Deng-ke, OU Yang-lu
(School of Business, Hunan University of Technology, Zhuzhou 412007, China)
This paper uses the intuitionistic trigonometric fuzzy number and the entropy weight method to calculate the comprehensive evaluation value of each evaluation attribute of the alternative logistics service provider by assembling the expert decision matrix, and then calculate the value of each scoring function value and the exact function value. The ranking of the evaluation value of the alternative logistics service providers is obtained, that is, the ranking of the comprehensive selection decisions of each logistics service provider is obtained.
logistics service provider; entropy weight; intuitionistic triangular fuzzy number; selection decision
F224
A
1674-3261(2020)01-0057-05
10.15916/j.issn1674-3261.2020.01.01
2019-06-13
徐登科(1962-),男,湖南益阳人,教授,硕士。
优先出版地址:http://kns.cnki.net/kcms/detail/21.1567.T.20191227.1040.018.html
责任编校:刘亚兵

