室内伪卫星信号多径微观参数统计模型

潘树国，王欣怡，蔚保国，夏 炎，高 旺

（1.东南大学 仪器科学与工程学院，南京 210096；2.卫星导航系统与装备技术国家重点实验室，石家庄 050081；3.中国电子科技集团公司第五十四研究所，石家庄 050081）

伪卫星作为可以发送类似轨道卫星信号的地面信号发射器，可以应用于室内独立组网定位[1]，但室内复杂的建筑结构和多变的实际环境使伪卫星应用于室内定位面临诸多困难。多径效应作为影响伪卫星定位精度的主要因素之一，因地域性和时变性较强而无法通过差分技术进行消除，因此现代商用接收机中通常使用的经典延迟锁定环路跟踪技术在密集多径环境中的性能较差。根据多径统计模型设计合适的滤波算法作为一种有效的多径抑制方法在移动通信卫星领域已经得到了广泛的应用，该方法同样适用于伪卫星室内定位，因此一个能全面描述伪卫星多径信号传播特性的统计模型为伪卫星室内定位算法改进和高精度定位的实现提供了研究基础。

多径作为影响接收机性能的重要因素，已经得到了广泛的研究。Kvicera M等人研究了L、S和C波段卫星信号在城市峡谷的穿透损耗，提出了在视距（LOS）和非视距（NLOS）传播条件下的高度依赖经验模型[2]。Jost T等人针对室内多径传播引起的接收功率，穿透损耗和进入损耗之间的确定性关系，提出了一种入口损耗模型，解决了标准穿透损耗模型中未考虑建筑布局与收发设备几何形状相互关系的问题[3]。Jost T等人提出了一种能够复制移动接收器宽带传播信道空间特性的新型宽带卫星信号室内信道模型[4]。Chen X等人详细阐述了关于多径信号生命周期的概念，提出了多径生命周期参数，并用多径生命时间概率分布模型来模拟城市峡谷中多径存在时间的统计特性[5]。Chen X等人又在后续的研究中深入分析了城市峡谷中三个关于多径的核心参数—延迟、功率和寿命，提出并验证了多径延迟遵循 Gamma分布，多径功率延迟分布遵循对数线性衰减模型，并且多径寿命遵循准指数减小[6]。

上述模型均是针对轨道卫星多径信号的统计模型，国内外学者针对伪卫星信号的多径效应也进行了类似的研究。Rusu-Casandra A等人研究了典型办公环境下的单路静态信道和多径衰落信道传播[7]。基于基带样本提出了 GPS伪卫星信号的时间延迟误差和相位分布在单路静态信道中均符合均匀分布的结论。Islam A K M N等人发现GPS伪卫星信号不能完全与已有的衰落信道模型完全匹配，因此提出一种包括Nakagami、Log-normal、Rayleigh和 Loo分布的组合加权模型[8]。Islam A K M N等人又在后续的研究中发现 GPS伪卫星信号在视距路径下，振幅服从Nakagami-m分布且相位服从均匀分布[9]。

上述模型均表征了伪卫星多径信号叠加后的传输特性，由于室内环境的复杂性以及从输出信号中分离出多径的难度较大，单条多径传播特性统计模型的研究较为罕见，即伪卫星多径“微观”参数的特征尚有待揭示，如多径信号的延迟、衰减、载波相位和数量等，这些参数能够更直接地反映多径的行为，不仅有助于提出更加有效的多径滤波算法，同时也为导航模拟器和接收机的多径识别与抑制提供了理论依据。

本文旨在研究伪卫星信号的三个多径“微观”参数，即延迟扩展、功率延迟和生命周期。针对伪卫星应用于室内定位多径微观参数传播特性未知的问题，本文主要提出了适用于伪卫星信号体制的多径微观参数理论模型，并运用确定性建模方法对伪卫星信号在典型室内结构化场景的传播过程进行仿真计算，通过将归纳统计得到的确定性模型与理论模型相匹配，从仿真角度验证了本文提出的理论模型的正确性。

1 伪卫星多径微观参数理论模型

在多径场景中，伪卫星信号在收发设备间存在分裂和叠加两种状态，本节综合考虑室内伪卫星信号体制特点及典型应用环境特征，结合已有的室内无线通信信号统计模型，提出了适宜于伪卫星信号体制的多径微观参数理论模型。

1.1 多径延迟扩展

伪卫星信号载波频率为1575.42 MHz，信号带宽与B1频段卫星信号相同为4 M，信号码宽约为977.5 ns。文献[10]证明了1500 MHz的无线信号在办公室环境中多径延迟的均方根为10～50 ns，因此伪卫星信号码宽远远大于室内无线信道的多径时延扩展经验值，从而伪卫星信号的多径时延扩展可以用平坦衰落来表征。

本文提出室内伪卫星信号的多径延迟扩展特性服从室内通信信号统计模型。该模型是基于窄带信道探测方法的统计结果，与伪卫星信号体制相符，且常用于描述室内无线信道中平坦衰落信号的统计时变特性，其概率密度函数可以用式(1)来表示[11]：

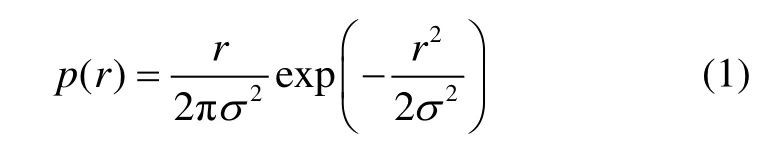
其中，r2=x2+y2为信号包络，σ2为方差，x和y为服从正态分布且相互独立的随机变量。

伪卫星多径成分与室内定位应用场景和伪卫星布局有关，上述模型根据多径成分的不同细分为以下三类：

① 当多径分量中杂波较少，视距信号为主信号且主导作用明显，其他多径分量较弱时，如大厅、走廊等障碍物较少的室内场景，其信号传播衰落情况可用莱斯分布来表征[12]。

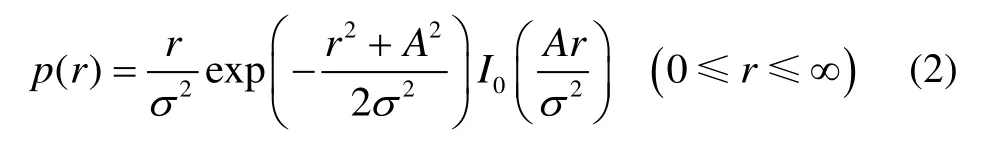
② 当多径分量中杂波严重，视距信号较少且主导作用不明显时，如停车场等障碍物适中的室内场景，其信号传播衰落情况服从瑞利分布。

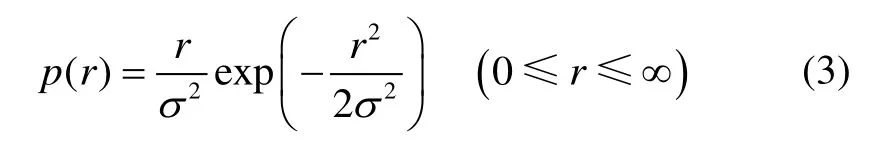
③ 当多径分量中杂波较少，平坦衰落不明显时，如办公室、图书馆等障碍物较多的室内场景，其信号传播衰落情况近似为对数正态分布。

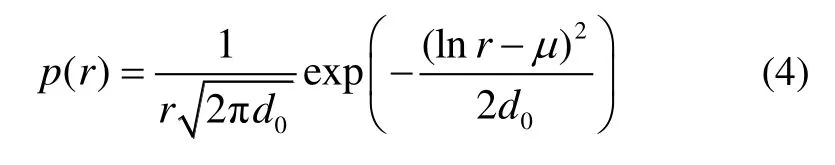
其中，μ为lnr的均值，dr为lnr的方差。

1.2 多径功率延迟

伪卫星信号接收功率为发射功率和路径损耗的差值。当发射功率恒定时，接收功率与路径损耗的变化趋势相反，因此，路径损耗模型对伪卫星多径功率延迟具有一定参考意义。

对于室内环境，基于1.8 GHz实测数据的衰减因子模型可用于预测与传输距离和特殊环境相关的伪卫星信号的路径损耗。衰减因子模型比较明确地考虑了每堵墙所引起的损耗，不仅考虑了距离相关的功率损耗，同时引入了地板衰减因子（FAF），针对一些具体的环境和室内设施所引起的损耗预测更加精确。具体如式(5)所示：

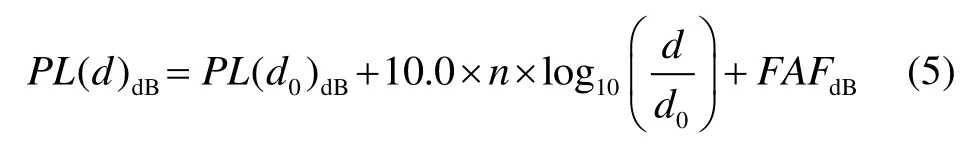
式中，d是收发设备之间的距离，d0是参考距离，n为路径损耗系数，FAFdB为地板衰减因子，PL(d0)dB是参考功率损耗。其值的计算可以参考式(6)[13]：

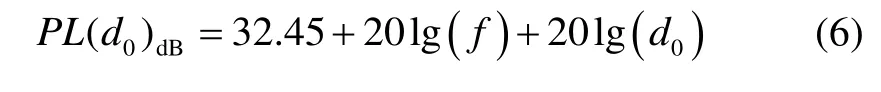
由式(5)可得，室内伪卫星信号的路径损耗随传输距离的增大呈指数增加，入射功率值固定不变，因此，本文提出室内伪卫星信号的多径功率延迟服从指数衰减。

1.3 多径生命周期

多径生命周期指多径从出现到消失的时间。影响多径生命周期的因素来自三个方面：障碍物尺寸，伪卫星、障碍物和接收天线之间的相对运动，以及障碍物的材料。

在文献[14]中，发射源是准静态的，安装在汽车上的接收装置是移动的，生命周期被定义为单个回波的存在时间内接收器移动的距离。在文献[6]中，发射器是不同轨道的卫星，接收装置是静止的，实验环境是密集的城市峡谷，生命周期被定义为接收器连续接收到的单个回波的存在时间。文献[6]中不同轨道多径生命周期的概率密度分布和累积密度分布与文献[14]存在相似的分布形状，说明了即使在不同的实验环境下，多径生命周期也具有相似的分布特性。

伪卫星信号与空间导航信号在电文、扩频码、调制方式上保持着较高的兼容性，因此两者的生命周期也应具有相似的分布特性，同时结合应用环境特征，本文提出短寿命多径大多为透射多径，长寿命多径分量属于反射多径。

2 确定性建模方法

本节提出了针对室内伪卫星多径信号的确定性建模方法。首先在典型室内结构化场景的环境特征和相关参数的研究基础上对室内环境进行场景分类建模；接着提出伪卫星多径信号的跟踪和提取方法，依据射线追踪法找到每对收发点之间的传播路径并计算与每条射线路径相关的复杂电场；最后代入式(7)～(13)依次计算出三种多径微观参数。

2.1 室内结构化场景建模

办公区域是一个易发生多径的环境，代表着一类布局复杂的室内场所，如商场、地下停车场等。因此，本文选择受到多路径严重影响的办公区域作为目标研究环境。

室内三维场景内墙体等实体信息的构建是确定性建模的首要步骤。本文选用Wireless Insite软件对办公区域进行三维场景建模。办公区按面积大小和空间复杂度被划分为四个区域，分别为面积最小、障碍物较少的接待区和面积较小、障碍物适中的封闭办公区，以及面积较大、障碍物适中的会议室和面积最大、障碍物最多的开放办公区。办公区域长50 m，宽30 m，高6 m，占地面积1500 m2，区域面积约为140～400 m2，办公家具高 1～3 m，办公区布局及家具材料均符合实际，具体参数详见表1。办公区域的2D/3D模型如图1和图2所示。

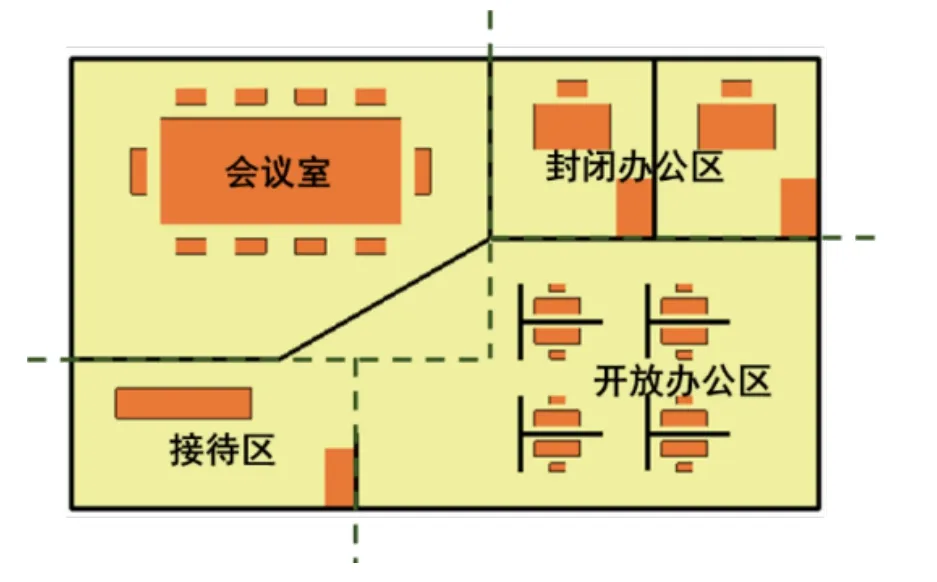
图1 办公区域2D模型Fig.1 Office area 2D model

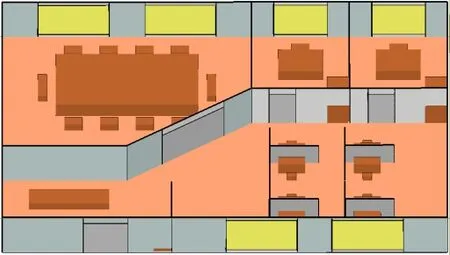
图2 办公区域3D模型Fig.2 Office area 3D model

表1 办公区域模型仿真参数Tab.1 Office area model simulation parameters

伪卫星发射装置布设于办公区的中心位置，为验证多径延迟与伪卫星高度角的相关性，以1 m为基准和步长均匀设置了6种不同高度的伪卫星发射点，发射天线为右旋圆极化全向天线，向外不间断辐射频率为1575.42 MHz的正弦波信号。

伪卫星数据采集点设有两种类型。类型一为9个特殊位置的数据采集点，其随机分布在四个区域，确保每个区域至少存在2个。类型二为遍历模型空间的数据采集点，用于探究多径功率延迟与空间位置的相关性，办公室区域被均匀划分为1500个等距网格，每个网格覆盖1 m2，且每个网格内有且仅有一个数据采集点。接收天线高度均为1 m，同样选用右旋圆极化全向天线。数据采集点及周围障碍物分布如图3所示。

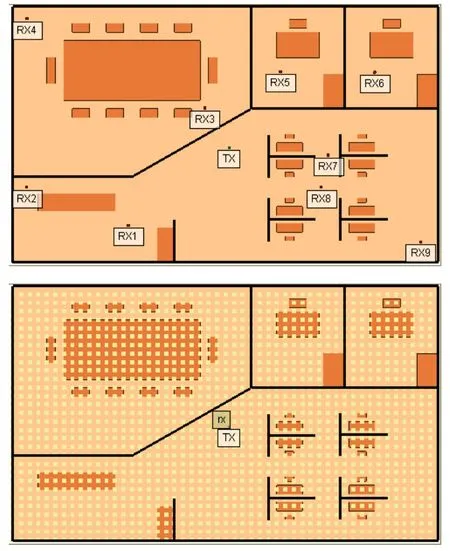
图3 数据采集点及障碍物分布Fig.3 Data collection points and obstacle distribution

2.2 多径信号的跟踪和提取

多径信号在室内结构化场景的跟踪和提取是确定性建模的第二步。

本文采用射线追踪法中具有较高实用价值的镜像法进行多径信号的跟踪。镜像法将伪卫星信号剖分成若干个几何射线管，然后依次进行射线管与室内模型中多面体面的相交测试，再根据镜像点与各平面的交点确定反射、绕射和透射射线管，接着判定射线管是否到达接收点，最终在接收点处根据障碍物形状以及材质相关的反射系数、绕射系数和透射系数计算伪卫星信号的场强分布，同时使用电场与特定天线相结合的方式进行特定场景的电参数计算[15]。镜像法流程图如图4所示。

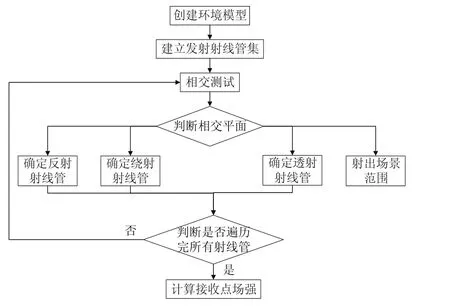
图4 镜像法流程图Fig.4 Flow chart of the mirroring method

在获得所有的信号分量后，需要对多径信号进行提取。接收机在采集伪卫星数据时，因无法区分直射信号和多径信号，各信号分量在接收端按各自的幅度和相位相互叠加，使伪距测量值产生严重误差[16]。然而，当多径相对于直射信号的衰减较大时引起的伪距测量误差通常可以忽略不计，数据接收设备只需要对强大的多径进行衰减，并且当信号分量衰减严重时，它们的参数估计在模型建立时误差较大。因此，本文在处理伪卫星信号实验数据时，为多径的提取设置了如下标准：

1）伪卫星发射点与数据采集点之间只存在一条视距路径，当视距路径之间存在障碍物时，直射径的信号强度往往小于其余信号分量，因此信号强度不作为本文直射径的判定条件。

2）直射径到达数据采集点用时最短，最先到达数据采集点的信号分量视为直射径，其余信号分量均视为多径信号。

3）多径信号相对于直射信号的最大衰减为20 dB，弱于此阈值的信号分量视为无效多径。

2.3 多径微观参数计算公式

多径微观参数的计算是确定性建模的第三步。用射线追踪法计算出每对收发点之间的传播路径及其复杂电场后，代入依据ITU无线通信标准推导得到的伪卫星多径微观参数计算公式[17]，就可以得到每条多径的延迟扩展、平均功率和传输时间。

1）多径延迟扩展

多径延迟扩展是时间延迟的功率加权均方根，用于量度多径的相关效应。伪卫星信号为窄带信号，每条多径的延迟扩展可以表示为：

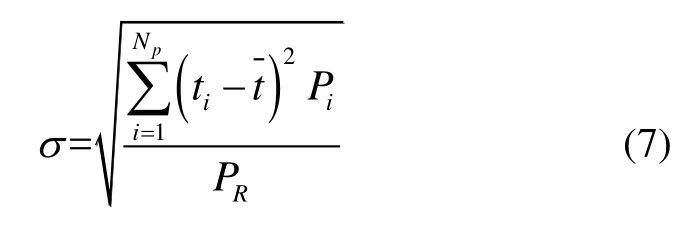
式中，Np为多径信号的数量,Pi为每条多径的平均功率，PR为接收点总功率，ti为每条多径的传输时间，t为平均到达时间，表示为：

2）多径平均功率

多径平均功率表明了每条多径的时间平均功率，可以表示为：

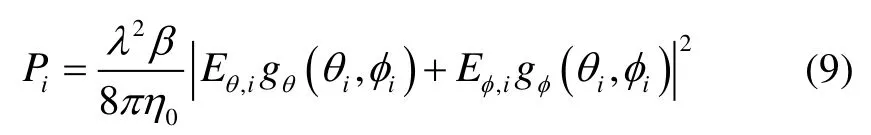
式中，λ为波长，η0为自由空间的阻抗（377Ω），Eθ,i和Eφ,i是接收点处第i条多径电场的θ和φ分量，gθ(θi,φi)和gφ(θi,φi)决定了每条多径的到达方向，可以表示为：

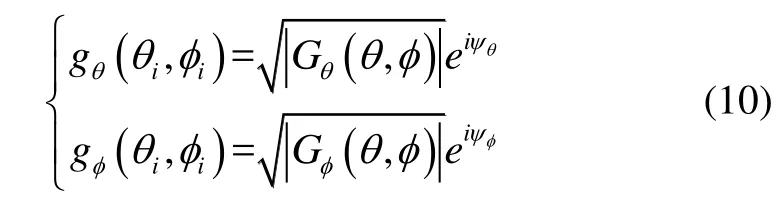
式中，Gθ和Gφ分别为接收天线增益的θ分量和φ分量，ψθ和ψφ分别是远区电场θ分量和φ分量的相对相位。

式(9)中，β是发射波频谱ST（f）与接收波频谱SR（f）的重叠，可以表示为：

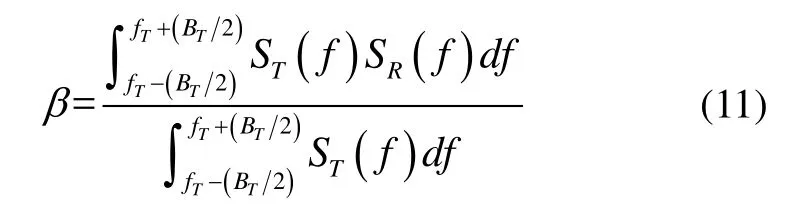
式中，fT和BT分别为发射波形的中心频率和带宽。伪卫星信号属于窄带信号，因此假定为平坦分布，S（f）表示为：

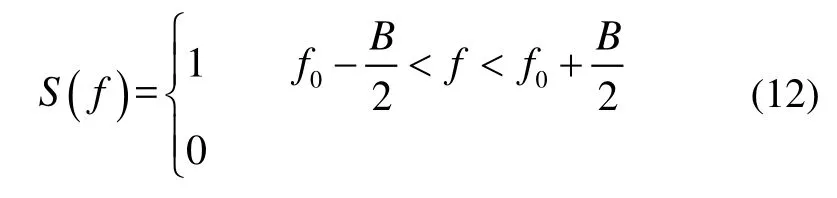
式中，f0为多径信号中心频率，B为信号带宽。

3）多径传输时间

每条多径的传输时间由下式给出：

式中，Li为几何路径的总长度，c为自由空间的光速。

3 确定性建模匹配验证

本节基于确定性建模方法对伪卫星信号在典型场景模型中的传播情况进行计算仿真，从实验环境中跟踪并提取多径进行数据推导和分析统计，建立相应的确定性模型来交叉验证本文提出的理论模型的正确性。

第一类数据收集点共采集到441条多径分量，第二类数据收集点共采集到73500条多径分量，无效多径分量共437条。提取的多径数量足以支持伪卫星信号确定性模型的建立。伪卫星多径信号的延迟扩展、功率延迟与生命周期是本文的主要研究参数。

3.1 多径延迟扩展

多径延迟扩展是特定场景（例如办公室）中多径信号相对于直射信号的延迟概率，表征了伪卫星信号传输的时间色散效应。该模型可以作为多径发生的预判，并且提供多径分量沿延迟维度分布的指南。提取类型一接收点的多径分量，根据式(7)计算可得，多径延迟的范围为0 m（最小值）到100 m（最大值），根据多径延迟的长度将这些多径数据分成20组，每组的延迟间隔为5 m。图5示出了伪卫星信号多径延迟的直方图。

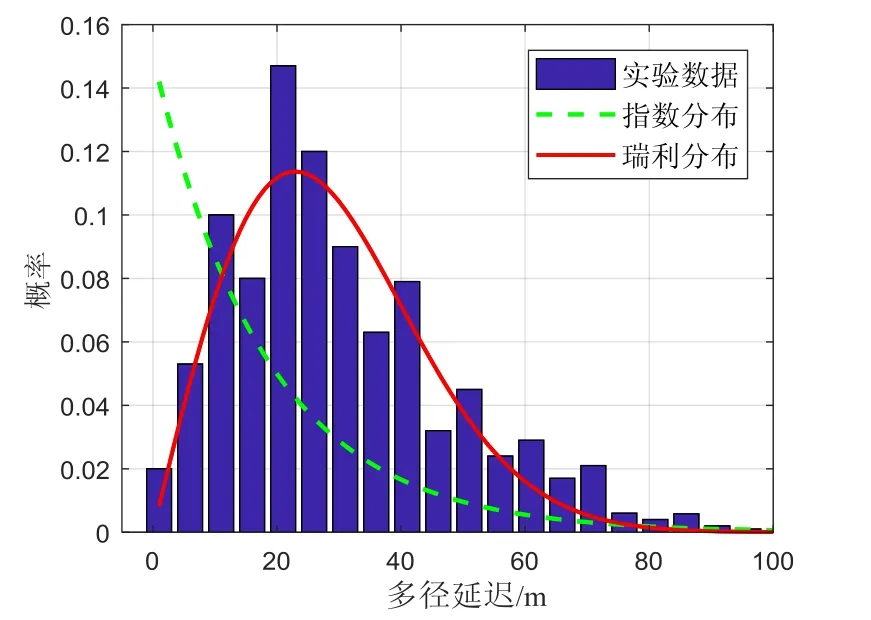
图5 多径延迟扩展概率模型Fig.5 Multipath delay distribution probability model

为得到多径延迟的分布规律，选择指数分布和瑞利分布函数来拟合实验数据直方图，使用回归曲线拟合技术以最小二乘法为标准获得每个候选分布函数的最优系数。均方根误差（RMSE）最小的候选分布函数视为最优匹配分布函数，均方根误差的计算如式(14)所示。两个候选分布函数的最佳特征参数和相应的RMSE值列于表2中。

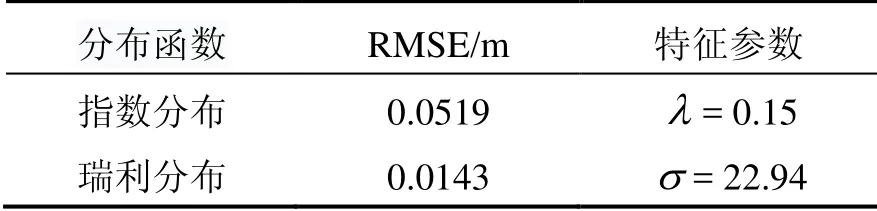
表2 多径延迟候选分布函数Tab.2 Multipath delay candidate distribution function

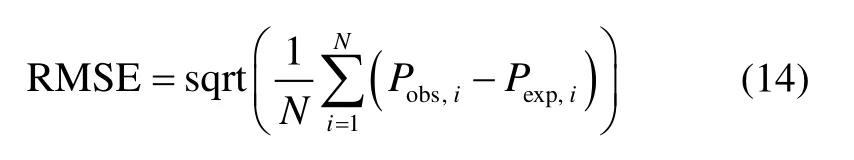
指数分布

瑞利分布

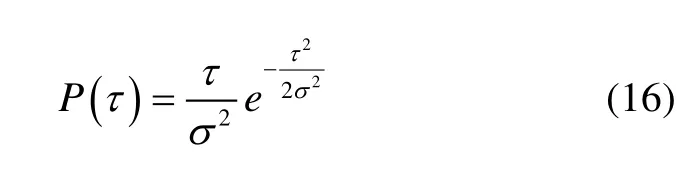
在以上两种候选分布函数中，指数函数是文献[6]采用的模型。由图5可知，指数分布在时延为0时具有最大的分布概率，这与实际经验相矛盾。通常认为，在实际的应用场景中，多径延迟在极大值或极小值处分布概率较小，而在时延的中间值处，分布概率应达到最大值。瑞利分布曲线与实际经验相符合，且与多径延迟的实际计算值RMSE值最小。因此，伪卫星信号的多径延迟扩展确定性模型服从瑞利分布，同时在该实验场景下多径分量杂波严重，视距信号较少且主导作用不明显，因此实验结果与 1.1节中理论多径延迟扩展模型相一致。

多径延迟还与直射信号和非直射信号的交叉角有关，这取决于伪卫星的高度角，即接收点至伪卫星的方向线与水平面的夹角。伪卫星布设高度受室内布局的影响，高度角范围大约为0°～60°，静态伪卫星天线高度角固定不变，不同高度角伪卫星所得的多径分量构成多径延迟分析的样本集，将其均匀划分成等间隔的区间，每个区间范围为10°，将多径数量计数到相应的高度角区间。图6示出了不同高度角范围的多径延迟分布规律。

由图6可知，不同高度角范围的多径延迟分布规律不完全相同，这表明多径发生概率在不同伪卫星高度角范围内是不同的。因此研究多径延迟与伪卫星高度角之间的相关性十分必要。伪卫星高度角在30°～60°之间时，多径延迟服从瑞利分布，多径延迟多发生在20～40 m之间，且高度角越大，长多径的发生概率越小。而当高度角低于30°时，多径发生概率随多径延迟的增加呈指数衰减。这是因为高度角过低时，入射信号不易被反射，并且更可能被障碍物阻拦后发生严重衰减。拟合分布函数的最佳特征系数和相应的RMSE值列于表3中。表中，高度角为0°～30°时，多径延迟服从指数衰减P(τ) =aebτ，其中，a为概率初始值，b为衰减常数。

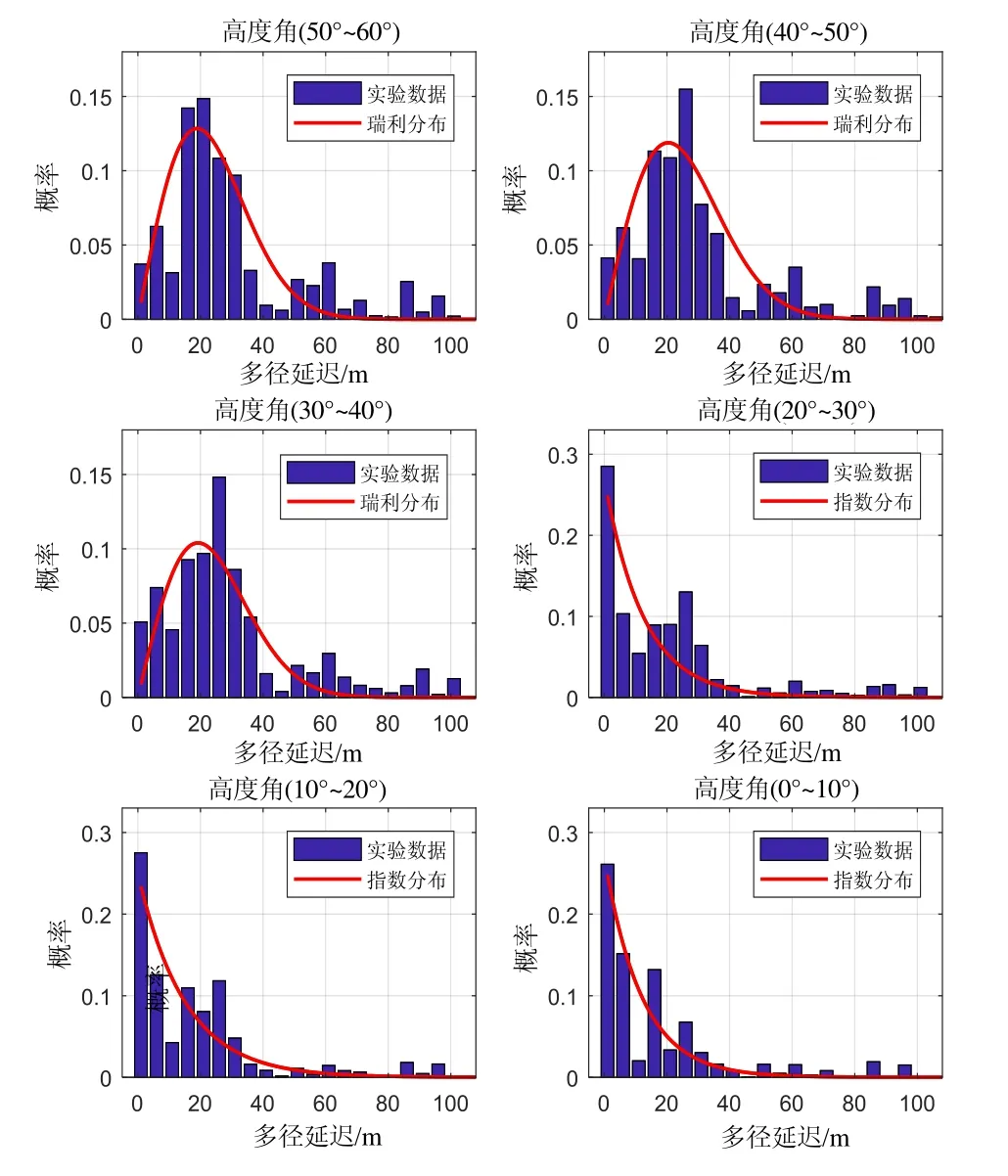
图6 不同高度角范围的多径延迟扩展Fig.6 Multipath delay distribution of different elevation ranges

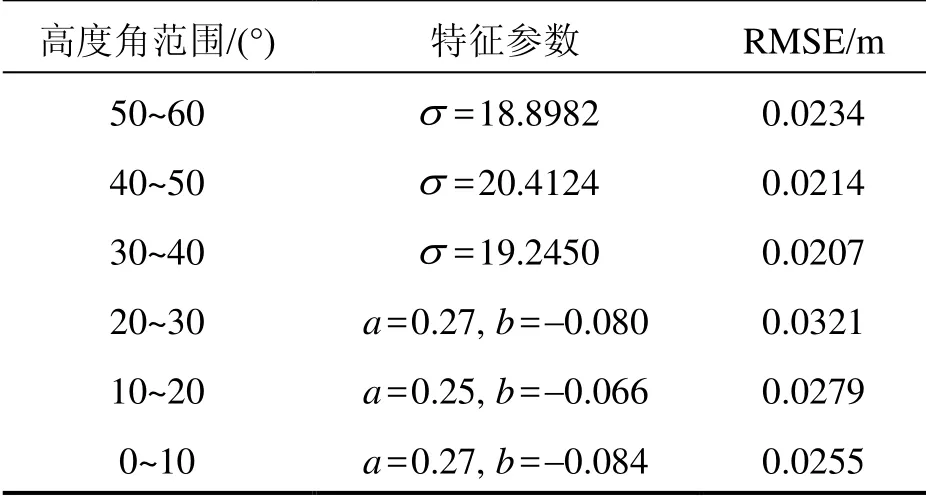
表3 不同高度角范围的多径延迟特征参数Tab.3 Feature parameters of multipath delay for different elevation ranges

3.2 多径功率延迟

多径功率延迟模型表征了伪卫星多径平均功率随多径延迟的变化规律。多径平均功率与信号频率、频谱重叠和电场分量等有关。根据式(9)，对图5中每个区间对应的类型一接收点的多径统计值求平均功率，得到如图7所示的功率延迟分布散点图。

由图7可知，伪卫星多径平均功率随延迟增加呈指数衰减，或在对数比例中表现为线性下降，多径功率延迟分布模型可以用式(17)(18)来表示：

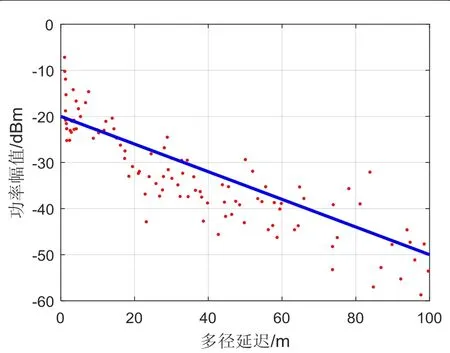
图7 多径功率延迟分布曲线Fig.7 Distribution curve of multipath power delay

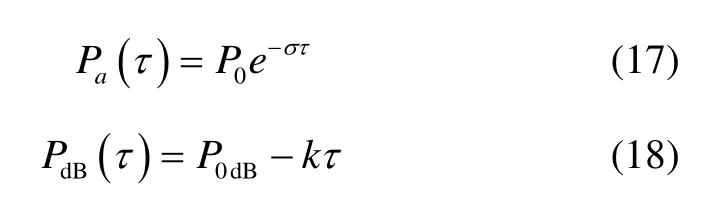
其中，σ=0.6908/m (k=-0.3dB/m)。P0= 1e-20/m(P0dB= -20dB/m)，该模型与文献[18]中论证的实验结果相吻合。因此，伪卫星信号的多径功率延迟确定性模型服从指数衰减，从而证明了 1.2节中本文提出的多径功率延迟理论模型的正确性。

图8是类型二接收点多径的统计结果，表示多径功率损耗与空间位置的作用关系，X、Y轴分别对应办公区模型的长和宽。由图8可知，多径功率损耗与空间复杂度相关性较大，障碍物越多多径功率损耗越严重。

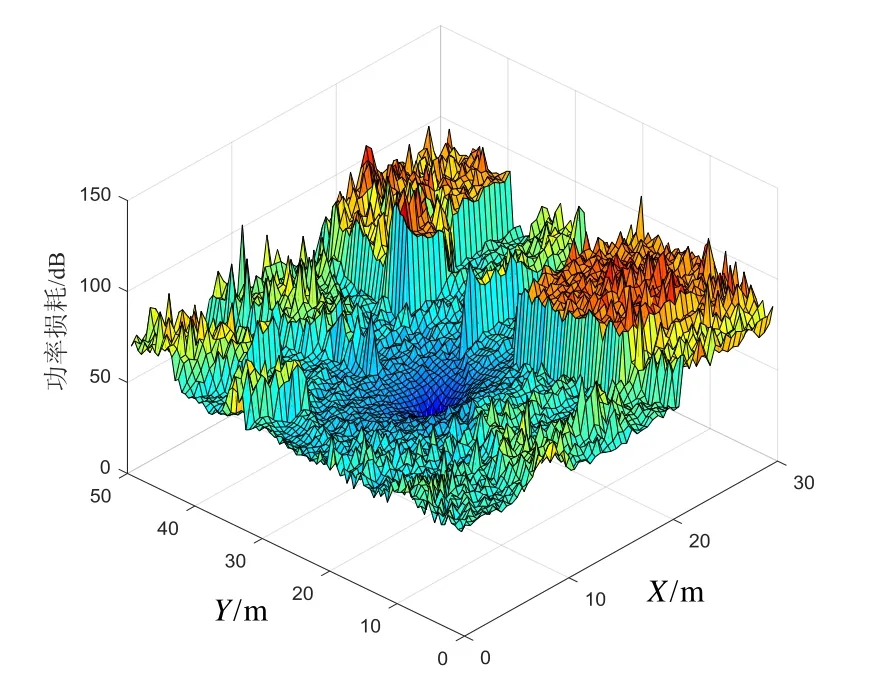
图8 多径平均功率衰减Fig.8 Multipath average power attenuation

3.3 多径生命周期

多径生命周期指多径从出现到消失的时间。本文研究静态伪卫星多径信号的生命周期，选择办公区域作为典型的室内结构化场景，大规模的办公设备及家具充当反射体的角色。由式(13)计算得到类型一接收点中每个多径分量的存在时间，将多径数量计数到相应的时间区间，得到如图9所示的直方图。

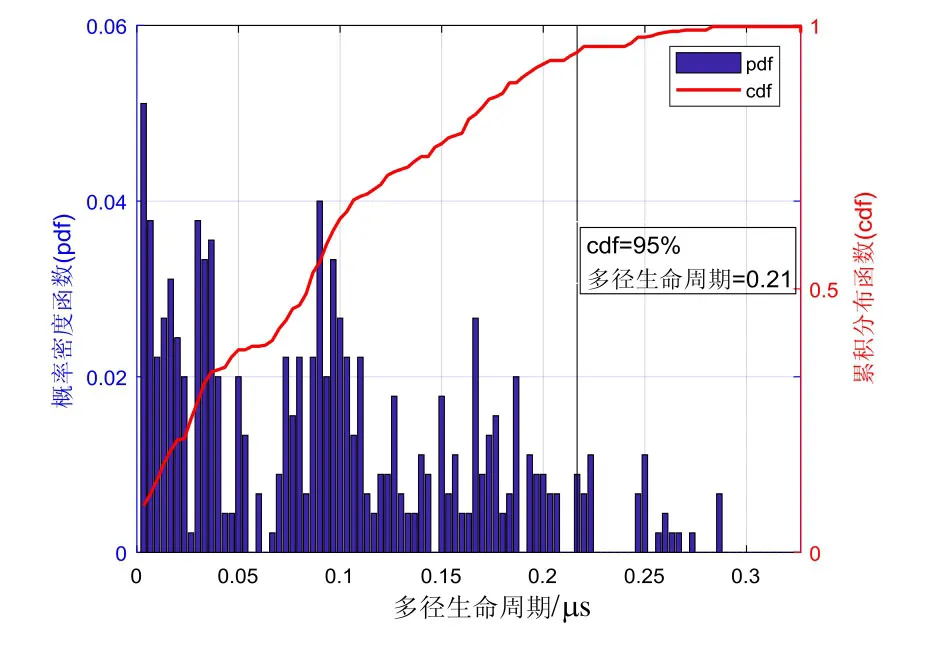
图9 多径生命周期分布曲线Fig.9 Multipath lifetime distribution curve

本次实验的样本集为431条多径的存在时间。多径存在时间覆盖0 μs到0.3 μs。整个时间范围以0.003 μs为步长被均分为100组，图9显示了多径生命周期的概率密度分布和累积密度分布。因实验环境中大量存在木材，混凝土等建筑结构，多径信号穿透这些材料时会产生4～30

dB的功率损耗，即使实验环境是静态的，多径生命周期仍远远小于1 s，最大传输距离大约为90 m。因此，透射多径大多属于短寿命多径，长寿命多径分量属于反射多径。在大约0.21 μs处，累积概率达到95%，大部分多径信号在65 m后消失。

4 结 论

本文通过将提出的伪卫星多径微观参数理论模型与确定性模型相结合，证明了多径延迟扩展模型符合瑞利分布，且多径延迟分布与伪卫星高度角有关。当伪卫星高度角在 30°～60°之间时，多径延迟分布曲线服从瑞利分布；当高度角低于 30°时，指数衰减能更好的解释多径延迟的分布特征。同时，伪卫星多径平均功率随延迟增加呈指数衰减，或在对数比例中表现为线性下降。在办公区域中，多径存在时间覆盖0 μs到0.3 μs，且透射多径大多属于短寿命多径，长寿命多径分量属于反射多径。上述结论进一步揭示了室内环境中伪卫星多径的信道特征，有助于伪卫星接收器和模拟器的设计。后续工作中，伪卫星信号多径参数在非结构化环境下的统计特性有待进一步研究。