基于精英蜂群算法的配电网故障恢复方法

李伦 李棕让 曹兴华 杨鑫 崔璨 朱宗峰 陈雪峰 宫德锋

摘要：  为缩短故障停电时间，降低停电损失，寻找最佳供电恢复方案，本文建立了配电网故障恢复数学模型，并引入精英蜂群算法，构建精英蜂群策略，改进侦查蜂搜索机制，得到配电网故障恢复的整体流程。同时，以某地市供电公司实际配电网系统故障恢复供电案例为例，分别采用标准人工蜂群算法（artificial bee colony， ABC）和精英蜂群算法对目标函数进行运算，并比较两种方法的可行性与优越性。研究结果表明，精英蜂群算法的收敛性能明显好于标准的ABC算法，其对配电网故障后重构的优化结果更好，是一种非常有效且非常实用的配电网故障恢复方法。该研究为配电网故障恢复方法研究提供重要参考，对社会经济的发展具有重要意义。

关键词：  配电网;故障恢复;精英蜂群;数学模型;案例分析;停电时间

中图分类号： TM642+.2; TM711  文獻标识码： A

配电网是电力输送的“最后十公里”，是国民经济和社会发展的重要公共基础设施，配电网的规模直接制约城市与农村的发展[1] 。近年来，配电网投资力度不断加大，但由于历史的原因，配电网尤其是中压配电网发展仍然滞后，城市与农村、东部与中西部电网发展不平衡问题依然突出[2] ，供电可靠性与国际先进水平仍有较大差距，存在着整体发展滞后与地区发展不平衡（城农不平衡、东中西部不平衡）的问题[3] 。由于自身因素的影响，配电网出现接地、跳闸等故障的频率较高，配电网故障直接导致电力用户失去电力供应，造成经济损失，影响供电公司品牌形象[4] 。为优化营商环境，保证用户电力供应，提供优化电能，配电网故障恢复方法研究成为电力系统研究的热点。马天祥等人[5] 针对交直流混合配电网特殊的网架结构和电气特性及交直流混合配电网故障恢复模型，研究了基于二进制粒子群算法的交直流混合配电网故障恢复方法，提出适用于交直流混合配电网故障恢复问的模型，模型应用适用较小，在传统交流配电网中应用较少;陈玮[6] 考虑主动配电网中风光机组出力不确定因素，将电动汽车作为应急调度资源，建立了一个形式为min-max-min的三层鲁棒数学模型，但模型中对配电网故障后恢复涉及较少;宋毅[7] 依托一体化电网规划设计平台，研究基于智能软开关的有源配电网供电恢复方法，在配电网发生故障并隔离后，智能软开关可为失电区域提供有效的电压支撑，该恢复方法结构较为复杂，推广应用存在一定难度。基于此，本文在配电网故障恢复方法中引入精英蜂群算法，利用其寻优率、求解精度高、收敛速度快等优点，以降低停电网损为目标，建立基于配电网故障恢复方法，并以某地市实际配电网部分网络结构为例，实际验证该算法的可行性与准确性，能够减少网损，对降低电力损失，为电力企业具有良好的经济效益。

1 配电网故障恢复数学模型

配电网可看成是由许多分段开关、联络开关及架空线路、电缆线路和用户组成，开关的闭合和断开都会造成网络拓扑结构的变化，配电网的重构通过调整开关状态来达到改变配电网拓扑结构的目的[8] 。实际运行中的系统都反映不同的运行条件，因此配电网需要根据具体的运行条件进行重构。

配电网故障恢复是一个复杂的工程问题，归根结底属于求解最优化问题[9] 。在进行故障恢复时，首先采用等效负荷模型简化网络，即把该问题转化为数学领域的问题。故障恢复由恢复目标和约束条件两部分组成，实际情况下可以按照不同的恢复目的和侧重点进行建模[10 11] 。配电网故障恢复模型为

minf S，X h S，X =0 g S，X ≤0 S∈T  （1）

式中，f（S，X）是所建立数学模型的目标函数，S是控制变量，X是状态变量;h是等式约束条件;g是不等式约束条件;T是所求问题的可行解空间。

1.1 建立数学模型

对所要求的故障恢复目标，建立如下数学模型：

1） 要求恢复的负荷量最多，即失电负荷最小，其目标函数为

minLout =∑ n0 i=1 Pi-PS （2）

式中，n0为停电区节点总数;Pi为停电负荷节点i的负荷量;PS为恢复方案的最大恢复容量;Lout 为失电负荷量。

2） 要求网损最小，其目标函数为

minSloss =∑ n k=1 I2kRk （3）

式中，Ik为线路k上的电流;Rk为线路k的电阻;n为支路总数。

3） 要求开关操作总数最少，其目标函数为

minNum=∑ n i=1 |xi-x′ i| （4）

式中，n为线路开关总数;xi为开关i故障前状态;x′i为恢复后的开关状态。

4） 以负荷均衡为目标，其目标函数为

minF=∑ n b=1 P2b+Q2b S2bmax  （5）

式中，n为网络中闭合的支路总数;Pb，Qb，Sbmax 分别为支路b的有功功率、无功功率及允许的最大容量。

1.2 约束条件

在恢复过程中，配电网故障要时刻满足如下约束条件：

1） 辐射状运行的网络约束为

gk∈Gk （6）

式中，gk为当前的网络结构;Gk是所有允许的辐射状网络配置集合。

2） 线路容量约束为

Il≤Ipl ， l=1，…，Li （7）

式中，Il是经过设备的电流;Ipl 为允许流过的电流上限;Li是设备总数。

3） 节点电压约束为

Uimin ≤Ui≤Uimax ， i=1，…，m （8）

式中，m为开关总数;Ui，Uimax ，Uimin 分别为开关i上的电压、电压最大值和最小值。

由以上分析可知，配电网故障恢复问题是一个包含约束条件的多目标非线性离散问题。本章采用改进蜂群算法的故障恢复模型，并可根据故障恢复目标的要求，建立目标函数。考虑网损和失电负荷，可建立目标函数为

minf=αLout +βSloss  （9）

式中，α和β分别为失电负荷量和网损权重;Lout 及Sloss 的求解见式（2）和式（3），该目标函数同样需要满足式（6）～式（8）所列的约束条件。

2 精英蜂群优化算法

蜂群算法的基本思想，首先将蜂群划分为引领蜂、跟随蜂和侦察蜂三种蜂种，然后随机生成初始种群，算法会在适应度值较优的一半个体周围进行搜索，采用一对一的竞争策略选择较优个体，该过程为引领蜂的搜索过程;利用轮盘赌选择法选取较优个体，并对其领域进行贪婪搜索，产生另一半个体，此过程称为跟随蜂的搜索过程[12 13] ;将引领峰和跟随蜂产生的个体组成新的种群，为避免种群多样性丧失，进行侦察蜂的类变异搜索，形成迭代群。与其他杂交优化算法相比，精英蜂群算法通过构建精英蜂群策略、改进侦察蜂搜索机制以及基于目標函数值选择寻优等方式，实现了精英蜂群算法能够加速算法收敛，同时不易陷入局部最优的效果[14] 。

2.1 精英蜂群策略的构建

采用按比例的适应度进行蜂群算法的选择，体现了生物学中“适者生存、优胜劣汰”的进化过程。智能算法在搜索最优解的过程中容易陷入局部最优，适当变异这些适应度值差的个体，可能会使算法跳出局部最优，最终收敛到全局最优[15 16] 。因此，精英蜂群通过选取排名前ζ%的精英蜂群，利用精英蜂群的记忆信息库，在蜂群位置发生变化时，一只精英蜂参与雇佣蜂和跟随蜂的局部位置更新，指导雇佣蜂和跟随蜂，此时精英蜂群受侦察蜂的全局引导，实现了优质食物源位置更新，达到了不易陷入局部最优的效果[17] 。新的雇佣蜂和跟随蜂位置更新策略为

υi，j =χe，j +φi，j w（χk，j -xave，j ） （10）

其中

φi，j =rand（-1，1）;ω= ωmax - iter MCN ωmax -ωmin  ; χave，j = ∑ D j=1 χi /D

式中，χe，j 表示精英蜂群随机一只精英蜂的第j维空间位置分量;ω表示精英蜂的权重系数;χave，j 表示蜜源第j维位置分量的平均之值;D表示空间维数。

2.2 改进侦查蜂搜索机制

传统人工蚁群算法设置是当食物接近枯竭时，雇佣蜂会转为侦查蜂来寻找新的食物源。将混沌序列算子和侦察蜂的历史经验值相结合来代替随机分布解空间，完成防止陷入局部最优的寻食过程[18] 。由于混沌序列具有较好的随机性和遍历性，本文基于混沌序列，在侦查蜂全局搜索时，结合历史搜索位置信息，对局部寻优进行指导，及时与跟随蜂完成信息交换，放弃跟随蜂寻觅到的枯竭食物源，开始新的蜜源搜索，重复以上过程，实现全局最优解。

1） 侦查蜂的初始分配方法。将各个解的可行域划分为ms等份，并将ms只侦查蜂分配于ms个子空间。设侦查蜂的初始位置[19] 为

χi，j （t0）=lbj+i（ubj-lbj）/m （11）

式中，i为侦查蜂的序号，i=1，2…ms，j=1，2…D。

2） 侦查蜂的侦查策略。由于侦查蜂需要在一定区域内四处游走寻找食物，因此其具有较强的随机性和遍历性。此外，该过程会受到以前经验位置的影响[20] ，因此本文算法引入混沌序列，体现侦查蜂的随机性和遍历性的特性。同时，由于该过程会受到历史侦查信息的影响，借鉴于粒子群算法，本文设置一个混沌搜索项来体现侦查蜂的随机性和大视域的遍历性，再设置一个启发项，来体现侦查蜂在寻找食物过程中所受到历史经验的影响。整个侦查蜂寻食过程为

xi，j （t+1）=xi，j （t）+r1（t+1） lbj+i （ubj-lbj） m + r2（t）（xg，j -xi，j （t））， i=1，2…，m， j=1，2…，D （12）

rk（t）=μ（rk（t-1）（1-rk（t-1）））， rk（t）∈（0，1）， k=1，2， rk（t0）=rand（0，1）， ms=γm （13）

式中，xi，j （t）为在解空间的当前位置;xi，j （t+1）为搜寻后的位置;rk（t）为两个不同混沌序列;rk（t0）为混沌序列的初值。

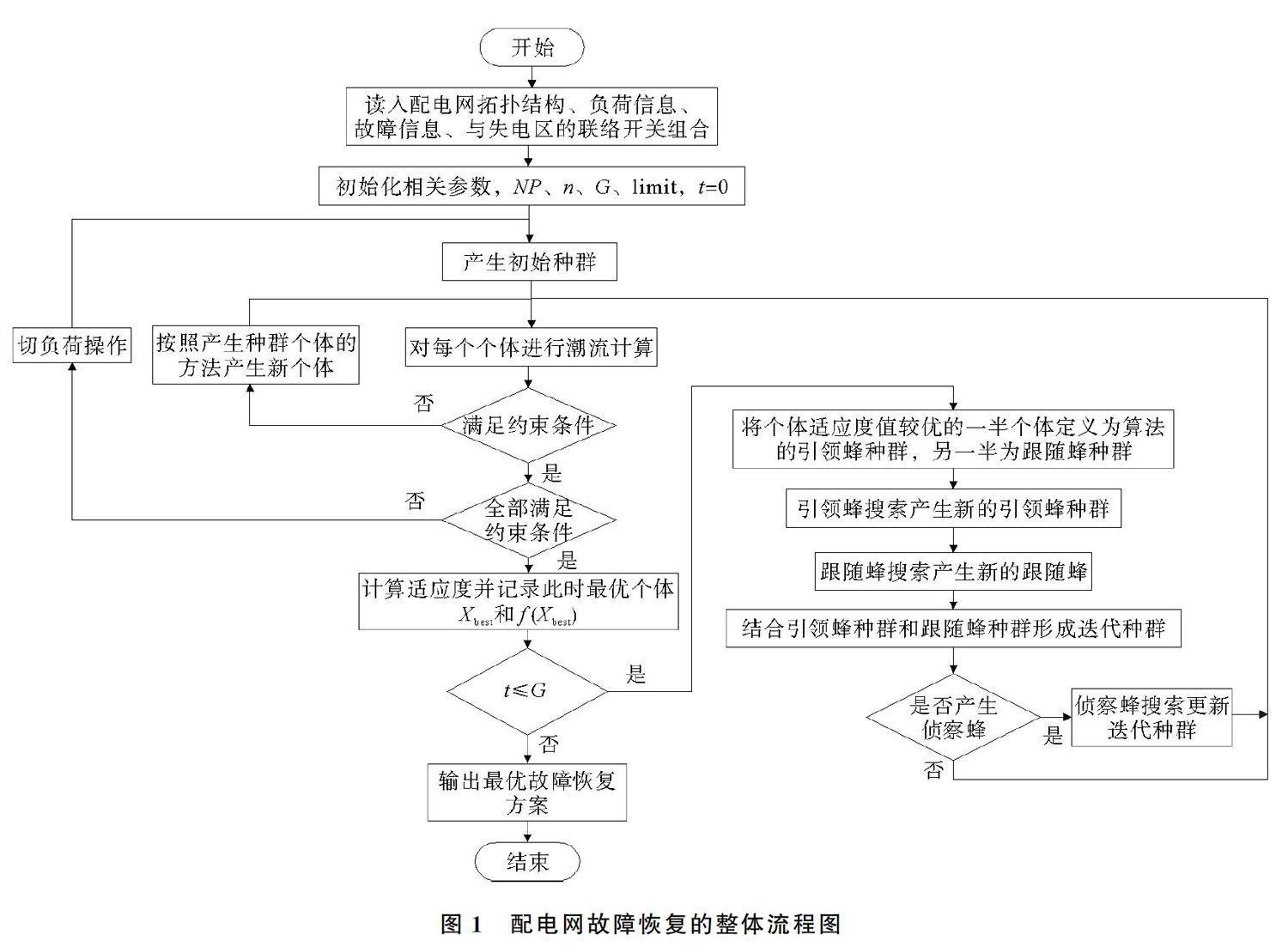
2.3 基于精英蜂群算法的配电网故障恢复整体流程

1） 根据配电网的拓扑结构来初始化参数，包括网络拓扑信息、负荷信息、故障信息、与失电区相连的联络开关、种群规模NP、雇佣蜂数me，侦查蜂数ms，引领蜂数mo，个体维数n和最大进化代数G，进化代数初始值t=0。

2） 根据式（11），对me只雇佣蜂进行初始化设置，并实现侦查蜂的分配，产生初始个体，根据潮流计算结果，检验结果是否满足约束条件，若满足，则进行下一步骤;否则放弃该个体，重复步骤2），直到满足种群规模NP，如果都不满足，则需要从末端进行切负荷。

3） 根据潮流计算结果，计算种群中个体的适应度函数值，选择其中的最优个体xtbest 和最优适应度值f（xtbest ） 。

4） 侦查蜂作大视域全局搜索，初始化混沌搜索项和启发项，根据式（11），求解每只侦查蜂的解空间位置，并完成边界检查和转换，求解ms只侦查蜂的适应度函数值。

5） 将适应度值较优的一半个体构成引领蜂种群，其余个体为跟随蜂种群。

6） 将引领蜂种群中的个体按式（12）和式（13）搜索，产生新个体，计算其适应度值，择优保留形成新的引领蜂种群。

7） 根据按适应度排序的蜜源，选择计算与xi相关的概率Pi。

8） 跟随蜂根据Pi，按式（12）和式（13）产生新解，形成跟随蜂种群，并计算其目标函数值。

9） 判断是否有连续nlimit 代没有发生变化的解，若有，则变为侦察蜂，用下式形成新解来替换较差的解，即

V（j）=xti（j）+（-1+2rand）（xti（j）-xtr1 （j））

10） 通过潮流计算，确定并记录本代种群最优个体和最优解。

11） 若满足终止条件，输出最优恢复方案，否则转至步骤4）。

配电网故障恢复的整体流程图如图1所示。

3 配电网故障恢复案例分析

本文以某地市供电公司实际配电网系统为例，该配电网络有46条支路，50个节点。其中，46条支路为不同型号的电缆接线，在区域内110 kV变电站中，有2台正常运行的110 kV/10 kV配电变压器，有2条110 kV进线，且与110 kV母线互为备用，2台10 kV变压器，出线通过联络开关B1连接。在网架结构内，共选取9个联络开关，标记为B1～B9。为计算方便，10 kV母线编号为3～50。同时，为了表示配电网中多电源的特点，将所选试点区域其他10 kV进线标记为10-1 ～10-9 。某地市供电公司实际配电网系统如图2所示。

当10 kV电缆线路遇到外力损坏、绝缘受潮、化学腐蚀等情况时，绝缘将会降低，从而被击穿，由此引发故障。例如，在所选配的电网区域内，母线3与14之间支路和母线43与45之间支路发生运行故障时，在遥控或人工切除该线路后，可以通过联络开关以及某些分段开关开合操作，调整配电网的运行方式，从而恢复非故障区域的供电。

由于该配电系统可以通过关闭联络开关，实现失电负荷为零和开关操作数少的目标，为了验证算法的收敛效果，本文以网损最小为目标，对配电网进行恢复供电，即故障后重构。网损最小的收敛效果如图3所示。利用式（3）所给出的目标函数，算法中种群规模为20，nlimit =D×ne×2，ne=NP/2为引领蜂个体数;温度T=1000，降温因子为η=0.95，终止温度为10;最大迭代次数为60次。分别采用标准ABC和精英蜂群算法，对目标函数进行运算，并比较两者的性能。由图3可以看出，精英蜂群算法的收敛性能明显优于标准ABC算法。

4 结束语

本文主要对基于蜂群算法的配电网故障恢复方法进行研究。針对网损最小，将改进后的蜂群算法与标准算法、遗传算法和粒子群算法进行仿真性能对比，仿真结果表明，在配电网故障后重构应用中，精英蜂群算法具有优越的收敛性能，电网重构效果得以优化。该算法在实际应用中具有良好的可行性与准确性，能够减少配电网故障后网损，节约电力资源，缩减电力成本，是一种非常有效并且非常实用的配电网故障恢复方法。该研究可为经济社会的发展带来巨大的经济效益。

参考文献：

[1] 张旭， 魏娟， 赵冬梅， 等. 电网故障诊断的研究历程及展望[J]. 电网技术， 2013， 37（10）： 2745 2753.

[2] 肖隆恩， 李闫远， 熊洋建， 等. 电网故障诊断的研究现状与发展趋势[J]. 通信电源技术， 2015（5）： 221 223， 226.

[3] 李春辉. 提高配网故障快速复电效率的思考与建议[J]. 科技与创新， 2014（18）： 23 24.

[4] 寇为刚， 李永祥， 孙艳军. 电力系统故障诊断的研究现状与展望综述[J]. 自动化与仪器仪表， 2015（2）： 4 6， 9.

[5] 马天祥， 王春英， 贾静然， 等. 基于二进制粒子群算法的交直流混合配电网故障恢复方法[J]. 电力系统保护与控制， 2019， 47（9）： 112 119.

[6] 陈玮. 模块化多电平柔性直流输电系统控制策略的研究[D]. 呼和浩特： 内蒙古工业大学， 2017.

[7] 宋毅， 薛振宇， 滕林， 等. 面向一体化配电网规划设计平台的数据集成技术研究及应用[J]. 电网技术， 2016， 40（7）： 2199 2205.

[8] 孙元博， 张承学， 胡志坚. 地区配电网重构与故障恢复问题[J]. 电网技术， 2014， 38（12）： 3366 3371.

[9] 洪小雨. 主动配电网故障恢复重构研究[D]. 北京： 北京交通大学， 2014.

[10] 许寅， 和敬涵， 王颖， 等. 韧性背景下的配网故障恢复研究综述及展望[J]. 电工技术学报， 2019， 34（16）： 3416 3429.

[11] 马瑞， 张海波， 王建雄， 等. 考虑负荷时变性的配电网故障抢修恢复策略[J]. 电力科学与技术学报， 2019， 34（2）： 20 27.

[12] 王林川， 李庆鑫， 刘新全， 等. 基于改进蚁群算法的配电网故障定位[J]. 电力系统保护与控制， 2008， 36（22）： 29 33， 53.

[13] 周坤. 改进的蚁群算法在城市配电网故障恢复中的应用研究[D]. 天津： 天津理工大学， 2015.

[14] 马卫， 孙正兴. 基于精英蜂群搜索策略的人工蜂群算法[J]. 计算机应用， 2014， 34（8）： 2299 2305.

[15] 李世光， 吴娆， 高正中， 等. 基于改进人工蜂群算法的配电网故障恢复[J]. 中国科技论文， 2016， 11（11）： 1269 1274.

[16] 左思然， 王中宇， 范闻博， 等. 一种改进的人工蜂群配电网状态估计方法[J]. 电测与仪表， 2018， 55（24）： 40 45.

[17] 高兆丽， 胥明凯， 丁素英， 等. 基于改进人工蜂群算法的配电网多点故障应急抢修优化调度[J]. 电力系统保护与控制， 2019， 47（13）： 107 114.

[18] ZHU Q B， YANG Z J， MA W. A quickly convergent continuousant colony optimization algorithm with scout ants[J]. Applied Mathematics and Computation， 2011， 218（5）： 1805 1819.

[19] Baraniuk R G. Compressive sensing [Lecture Notes][J]. IEEE Signal Processing Magazine， 2007， 24（4）： 118 121.

[20] Candes E J， Wakin M B， Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine， 2008， 25（2）： 21 30.

Distribution Network Fault Recovery Method Based on Elite Bee Colony Algorithm

LI Lun， LI Zongrang， CAO Xinghua， YANG Xin， CUI Can， ZHU Zongfeng， CHEN Xuefeng， GONG Defeng

（Taian Electric Power Dispatching and Communication Centre， Taian 271000， China）

Abstract：  After the fault occurs in the distribution network， it is necessary to isolate the fault area， and restore the power supply to the non-fault area according to the current network structure and power flow distribution and satisfying the relevant constraints. In order to shorten the outage time and reduce the outage loss， and find the best power supply recovery scheme， this paper introduces elite bee colony algorithm and establishes the corresponding algorithm flow. The feasibility and superiority of this method are verified by comparing the actual distribution network fault recovery power supply cases of a city power supply company. The application effect of this method in practical application is counted and the economic benefits of this method are verified. It provides an important reference for the research of fault recovery methods of distribution network.

Key words： distribution network; fault recovery; elite bee colony