单晶悬臂梁式压电振子的尺寸优化与研究

王乐生 王海峰 王世龙 李海宁

摘要：  为研究悬臂梁式压电振子的发电能力与自身结构尺寸的关系，本文将3种不同形状的基板（矩形、梯形、三角形）与3种不同形状的压电片（矩形、梯形、三角形）排列组合成6种不同形式的单晶悬臂梁式压电振子，并建立6种不同形式的压电悬臂梁有限元模型，利用ANSYS有限元分析软件，对压电片尺寸、基板尺寸和压电片位置进行仿真分析。仿真结果表明，矩形基板、梯形基板和三角形基板的悬臂梁，其压电片与基板的最佳长度比分别为0.15，0.25和0.35，其最佳厚度比分别为0.75，0.75～1和1;压电片为三角形悬臂梁的电压输出与压电片的厚度成正比，而压电片为其它形状的悬臂梁，随着压电片厚度的增加，其电压输出先增后减;压电悬臂梁的电压输出与压电片的宽度、基板的宽度和厚度以及压电片到基板固定端的距离成反比，与基板的长度成正比。该研究为相关领域的科研人员提供了理论支撑。

关键词：  单晶压电振子; 变截面悬臂梁; 静力学分析; 尺寸优化; 压电俘能; ANSYS

中图分类号： TN384  文献标识码： A

随着微型低功耗电子元器件的发展，与之相关的微能源技术逐渐引起研究界的重视[1] 。对于微型电子器件，传统的化学燃料电池因其具有体积大、寿命有限和不易拆卸等缺点，无法满足工程需要[2 3] ，因此，从周围环境中获取能量受到了研究界的广泛关注。环境中的能源包括太阳能、风能、机械振动能等[4 7] ，其中机械振动能较前两种能量更加稳定与持久。通过机电转换系统，将机械振动能转换为电能，可为微电子器件供能。目前，主流的振动俘能分为电磁式、静电式和压电式三种[8 9] 。与前两种方式相比，压电式因其具有能量密度大、受电磁干扰小、稳定性更好的优势而受到研究界的青睐[10] 。谢真真[11] 对矩形压电悬臂梁的结构尺寸进行了优化，总结出矩形压电悬臂梁的发电能力与结构尺寸的关系，但未对多种不同结构形式悬臂梁的发电能力进行总结归纳;费立凯[12] 对不同结构形式悬臂梁的输出电压与厚度比的关系进行分析，但未分析长度和宽度等要素;马小青等人[13] 分析了质量块位置对压电悬臂梁发电性能的影响，发现质量块存在一个最佳位置，使装置开路电压和输出功率最大;刘祥建[14] 对变截面悬臂梁的发电性能进行研究，发现压电梁夹角的增加将使其开路电压先增大后减小;卫海霞等人[15] 对压电片的位置和尺寸进行研究，确定了在一階模态下压电片的最佳尺寸; 邓冠前[16] 主要对不同形状压电振子的振动发电行为进行研究，但未对不同基板下不同压电振子的发电情况进行研究分析。基于此，本文将3种不同形状的基板与3种不同形状的压电片组合成6种不同形式的压电悬臂梁，研究基板和压电片的长度、宽度、厚度及压电片的位置对压电悬臂梁电压输出的影响。通过该研究来探究其内在规律和最佳组合方式，为不同形式压电片基板组合进入市场提供数据支撑。

1 压电悬臂梁的结构及工作原理

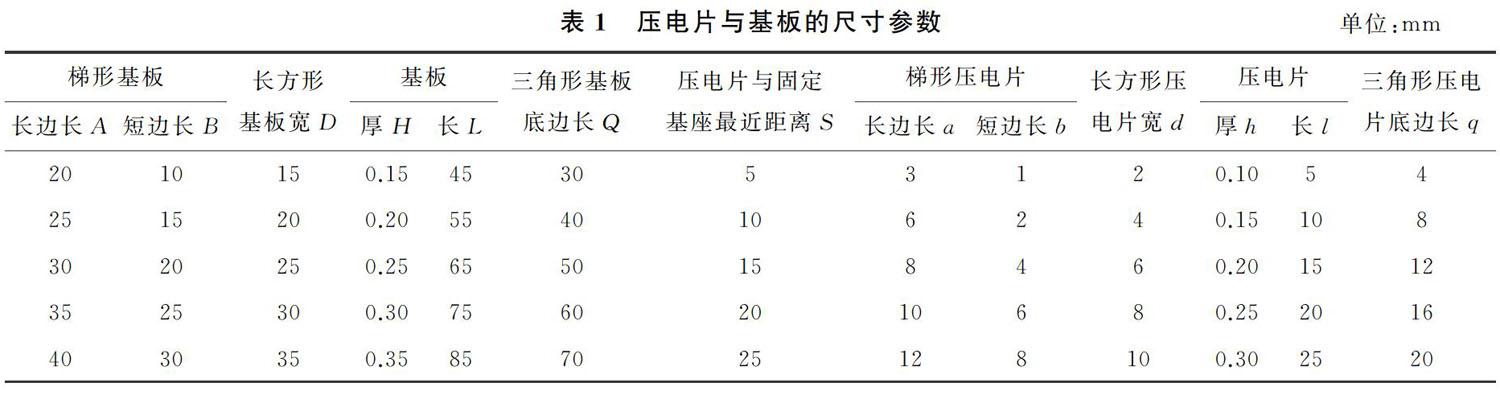
由于6种不同形式压电悬臂梁的工作原理相同，因此可用同一结构表示，悬臂梁结构示意图如图1所示。由图1可以看出，压电悬臂梁是由固定基座、基板及压电片三者组成。其中，L和H分别为基板长度和厚度，l和h分别为压电片长度和厚度，F是作用在自由端、方向为Z轴正方向的力，F=0.2 N，悬臂梁的左端为固定端。由于基板与压电片的几何形状相似，基板和压电片的结构示意图如图2所示。图2中，大写字母代表基板尺寸，小写字母代表压电片尺寸。仿真分析时，压电片与基板的尺寸参数如表1所示。

当压电悬臂梁工作时，自由端因外界环境振动而发生受迫振动，使压电悬臂梁发生弯曲变形，从而引起压电片内应力的变化，在其表面生成自由电荷[17 18] 。压电片所受应力与产生电场的关系为[19 20]

{ S }=[ s E]{ σ }+[ d ]{ E } （1）

{ D }=[ d ]{ σ }+[ ε T]{ E } （2）

式中，{ S }为应变向量;{ D }为电荷密度向量;{ E }为电场强度向量;{ σ }为应力向量;[ ε T]为应力恒定时的自由介电常数矩阵;[ s E]为电场恒定时的短路弹性柔顺系数矩阵;[ d ]为压电应变常数矩阵。

2 有限元模型

本文基板材料选用铜合金，压电材料选用PZT 5H。压电悬臂梁基板与压电片的材料参数如表2所示，给出6种不同形式的压电悬臂梁有限元模型，压电悬臂梁有限元模型如图3所示。

3 仿真分析

3.1 压电片尺寸的优化

当进行压电片尺寸优化分析时，设置矩形基板的长度L=60 mm，宽度D=20 mm，厚度H=0.2 mm;梯形基板下底A=30 mm，上底B=10 mm，高L=60 mm，厚度H=0.2 mm;三角形基板底边长度Q=40 mm，高L=60 mm，厚度H=0.2 mm。当进行长度分析时，设置矩形压电片的宽度d=8 mm，厚度h=0.2 mm;梯形压电片下底a=10 mm ，上底b=6 mm ，厚度h=0.2 mm ;三角形压电片底边长度q=16 mm ，厚度h=0.2 mm。当进行宽度分析时，设置矩形压电片的长度l=25 mm，厚度h=0.2 mm;梯形压电片的高l= 25 mm，厚度h=0.2 mm;三角形压电片的高l=25 mm，厚度h=0.2 mm;当进行厚度分析时，设置矩形压电片的长度l=25 mm，宽度d=8 mm;梯形压电片的下底a=10 mm，上底b=6 mm，高l=25 mm;三角形压电片的底边长度q=16 mm，高l=25 mm。通过ANSYS进行仿真分析，最终得到各个组合中，压电片长度、宽度、厚度与输出电压的关系曲线分别如图4～图6所示。

3.2 基板尺寸的优化

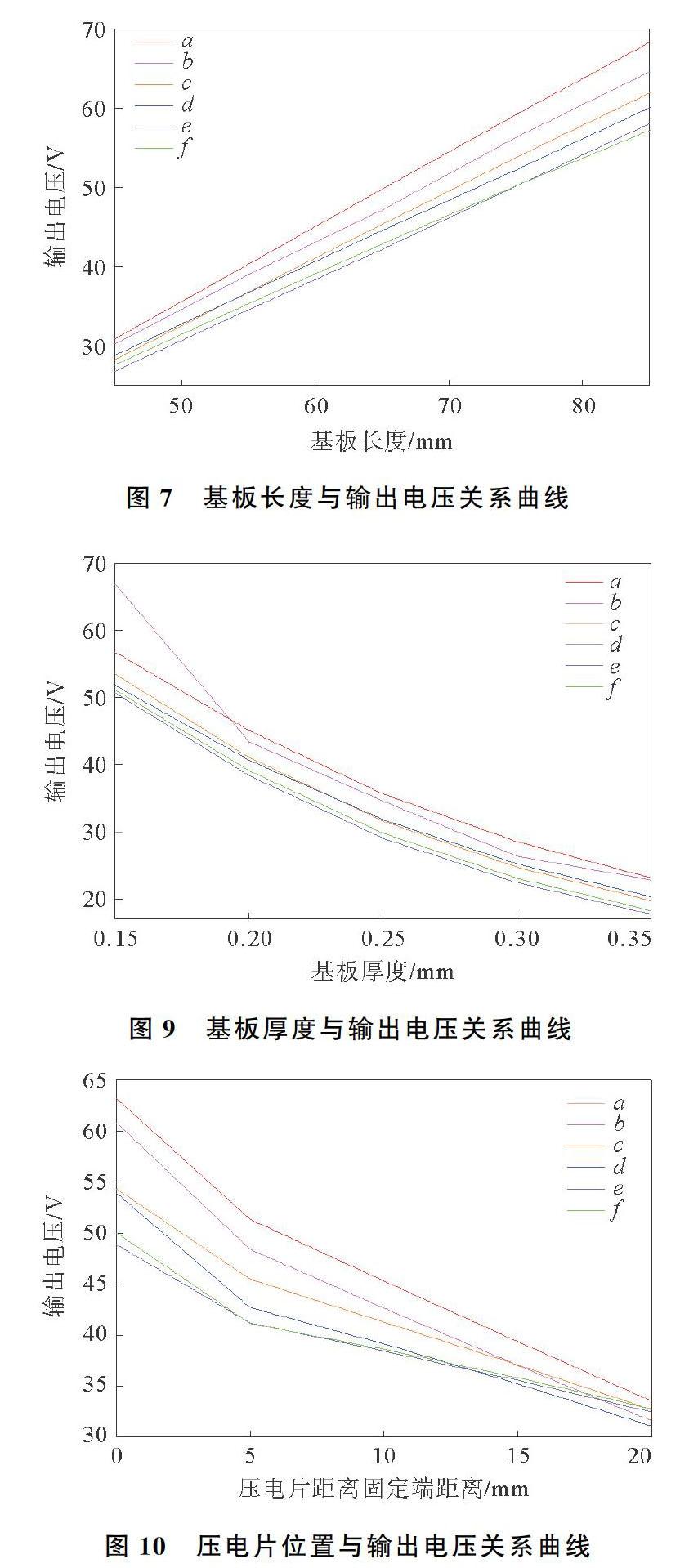
当进行基板尺寸的优化分析时，设置矩形压电片的长度l=25 mm，宽度d=8 mm，厚度h=0.2 mm;梯形压电片的下底a=10 mm，上底b=6 mm，高l=25 mm，厚度h=0.2 mm;三角形压电片的底边长度 q= 16 mm ， 高l=25 mm ，厚度h=0.2 mm 。当进行长度分析时，设置矩形基板的宽度D=20 mm ，厚度H= 0.2 mm;梯形基板下底A=30 mm，上底B=10 mm，厚度H=0.2 mm;三角形基板底边长度Q=40 mm，厚度H=0.2 mm。当进行宽度分析时，设置矩形基板的长度L=60 mm，厚度H=0.2 mm;梯形基板的高L=60 mm，厚度H=0.2 mm;三角形基板的高L=60 mm，厚度H=0.2 mm;当进行厚度分析时，设置矩形基板的长度L=60 mm，宽度D=20 mm;梯形基板的下底A=30 mm，上底B=10 mm，高L=60 mm;三角形基板的底边长度Q=40 mm，高L=60 mm。通过ANSYS进行仿真分析，得到各个组合中基板长度、宽度、厚度与输出电压的关系曲线分别如图7～图9所示。

3.3 压电片位置的优化

通过ANSYS进行仿真分析，最终得到各个组合中压电片位置与输出电压关系曲线如图10所示。在进行压电片位置优化分析时，设置矩形基板的长度L=60 mm，宽度D=20 mm，厚度H=0.2 mm;梯形基板的下底A=30 mm，上底B=10 mm，高L=60 mm，厚度H= 0.2 mm;三角形基板的底边Q=40 mm，高L=60 mm，厚度H=0.2 mm;矩形压电片的长度l=20 mm，宽度d=5 mm，厚度h=0.2 mm;梯形压电片的下底a= 7 mm，上底b=3 mm，高l=20 mm，厚度h=0.2 mm;三角形压电片的底边长度q=10 mm，高l=20 mm，厚度h=0.2 mm。

4 结束语

本文主要对单晶悬臂梁式压电振子的尺寸进行优化分析，建立了6种不同形式的压电悬臂梁有限元模型，并采用ANSYS软件进行仿真分析。仿真结果表明，矩形基板的电压输出比其他形状基板的电压输出高，与市场上主流基板形状一致。电压输出与基板的厚度、宽度和压电片到固定端的距离成反比，与基板的长度成正比，符合基本的力学规律。压电片为三角形的悬臂梁在压电片厚度达到一定值后会随着压电片厚度的增大急剧增加，该研究为从事相关领域研究的科研人员研发新型压电片形状提供了思路和数据支撑。下一步将考虑通过添加负载来探究功率与不同形式悬臂梁式压电振子的关系。

参考文献：

[1] Beeby S P， Tudor M J， White N M. Energy harvesting vibration sources for microsystems applications[J]. Measurement Science and Technology， 2006， 17（12）： 175 195.

[2] 袁江波， 谢涛， 单小彪， 等. 压电俘能技术研究现状综述[J]. 振动与冲击， 2009， 28（10）： 36 42.

[3] 陈定方， 孙科， 李立杰， 等. 微型压电能量收集器的研究现状和发展趋势[J]. 湖北工业大学学报， 2012， 27（4）： 1 8.

[4] Roundy S， Steingart D， Frechette L， et al. Power sources for wireless sensor networks[J]. Lecture Notes in Computer Science， 2004， 2920： 1 17.

[5] Whalen S， Thompson M， Bahr D， et al. Design， fabrication and testing of the P3 micro heat engine[J]. Sensor and Actuators A： Physical， 2003， 104（3）： 290 298.

[6] Pascal H， Xavier A， Thomas A. Energy harvesting from galloping of prisms： A wind tunnel experiment[J]. Journal of Fluids and Structures， 2017， 70： 390 402.

[7] Fu Y， Wang G， Mei T， et al. Accessible graphene aerogel for efficiently harvesting solar energy[J]. ACS Sustainable Chemistry and Engineering， 2017， 5（6）： 4665 4671.

[8] 王二萍， 高景霞， 张金平， 等. 压电俘能器研究现状及新发展[J]. 电子元件与材料， 2015， 34（9）： 18 24.

[9] Yoon S H， Lee Y H， Lee S W， et al. Energy-harvesting characteristics of PZT-5A under gunfire shock[J]. Materials Letters， 2008， 62（21/22）： 3632 3635.

[10]  Jansen A J， Fridstedt S， Weernink A J W， et al. A batteryless remote control for volvo， results of a fessibility study[C]∥ ISATA 2000 Conference Automotive & Transportation Technology. Dublin， Ireland： ISATA， 2000： 1 9.

[11] 謝真真. 压电悬臂梁振动能量收集器结构设计及实现[D]. 武汉： 华中科技大学， 2011.

[12] 费立凯. 压电悬臂梁式振动能量收集技术研究[D]. 北京： 华北电力大学， 2013.

[13] 马小青， 龚立娇， 潘巧生， 等. 质量块位置对压电悬臂梁发电性能影响分析[J]. 压电与声光， 2018， 40（5）： 789 792， 798.

[14] 刘祥建. 变截面压电单晶梁发电性能研究[J]. 机械工程与自动化， 2014（5）： 94 96.

[15] 卫海霞， 王宏涛. 悬臂梁能量回收装置压电片位置与尺寸优化研究[J]. 压电与声光， 2016， 38（2）： 235 240， 245.

[16] 邓冠前， 陈仲生， 陶利民. 不同形状压电振子的振动发电行为[J]. 压电与声光， 2010， 32（3）： 440 446.

[17] 許颖颖， 龚俊杰， 宋子玲， 等. 悬臂梁压电发电装置的实验研究[J]. 机械工程与自动化， 2012（1）： 80 81， 84.

[18] 单小彪， 袁江波， 谢涛， 等. 不对称悬臂梁压电发电装置的实验研究[J]. 压电与声光， 2010， 32（4）： 608 610， 614.

[19] Erturk A， Inman D J. On Mechanical modeling of cantilevered piezoelectric vibration energy harvesters[J]. Journal of Intelligent Material Systrms and Structures， 2008， 19（11）： 1311 1325.

[20] 曲远方. 功能陶瓷的物理性能[M]. 北京： 化学工业出版社， 2007： 183 185.

Size Optimization and Research of Unimorph Cantilever of Piezoelectric Oscillator

WANG Lesheng， WANG Haifeng， WANG Shilong， LI Haining

（School of Electromechanic Engineering， Qingdao University， Qingdao 266071， China）

Abstract：  In order to study the relationship between the power generation capacity of the cantilever beam piezoelectric Oscillator and it′s structuralsize， this paper arranges three different shapes of substrate （rectangle， trapezoid， triangle） and three different shapes of piezoelectric sheets （rectangle， trapezoid， triangle）， and combines into six different forms of unimorph cantilever beam piezoelectric Oscillator， and establishes 6 different forms of piezoelectric cantilever beam finite element models. It uses ANSYS finite element analysis software to determine the size of the piezoelectric sheet， the size of the substrate and the position of the piezoelectric sheet Perform simulation analysis. The simulation results show that for the cantilever beams of rectangular， trapezoidal， and triangular substrates， the best length ratios of the piezoelectric sheet to the substrate are 0.15， 0.25 and 0.35， and the best thickness ratios are 0.75， 0.75～1 and 1 respectively;The voltage output of the piezoelectric sheet which is a triangular cantilever beam is proportional to the thickness of the piezoelectric sheet while the piezoelectric sheet is a cantilever beam of other shapes. As the thickness of the piezoelectric sheet increases， the voltage output first increases and then decreases; The voltage output of the piezoelectric cantilever beam is inversely proportional to the width of the piezoelectric sheet， the width and thickness of the substrate， and the distance from the piezoelectric sheet to the fixed end of the substrate， and is directly proportional to the length of the substrate. This research provides theoretical support for researchers in related fields.

Key words： unimorph piezoelectric oscillator; variable cross-section cantilever beam; static analysis; size optimization; piezoelectric energy capture; ANSYS