输电塔风振响应双调谐质量阻尼器优化控制研究∗

刘石 张志强 黄国栋 温作鹏 楼文娟

(1.广东电科院能源技术有限责任公司 广州510080；2.广东电网有限责任公司电力科学研究院 广州510080；3.广东电网有限责任公司湛江供电局 524005；4.浙江大学建筑工程学院 杭州310058)

引言

输电塔是电力系统的重要结构，其安全性对现代社会正常运转至关重要。强风引起的输电线路的破坏在我国时有发生[1，2]，造成了严重的经济损失。因此，采用有效的风振控制措施以降低输电塔风振响应，对减少输电线路的破坏、保障电力安全具有重要意义。

调谐质量阻尼器(tuned mass damper，TMD)作为一种常见的减振装置，在桥梁、高层建筑风振控制方面已有较多研究[3，4]，而在输电塔的抗风设计中研究相对较晚。袁俊等[5]针对加装TMD的大跨越钢管塔展开研究，结果表明TMD 对输电塔动力响应的控制效果略优于粘弹性阻尼器。雷旭等[6]针对输电塔气弹模型设计小型电涡流TMD，并展开风洞试验研究，验证了 TMD 对输电塔不同方向的减振效果。

但TMD 存在减振效果对主结构频率摄动较为敏感的缺点。而研究表明，结构频率会受风速、温度、锈蚀等因素影响而变化[7，8]。此外在输电塔结构长期服役过程中，其结构可能有所损伤导致频率变动。因此，设计一种对结构频率摄动具有较强鲁棒性的阻尼器显得尤为重要。

多重调谐质量阻尼器(multiple tuned mass damper，MTMD)因其具有分布频率，对主结构有较强的减振鲁棒性，许多学者对此进行了研究[9-11]。但 MTMD 构造较为复杂，应用不便。在众多MTMD 形式中，双调谐质量阻尼器(double tuned mass damper，DTMD)由于其相对简单的构造与较强的鲁棒性具有较好的应用前景。Li等[12]针对单自由度结构-DTMD 系统，考虑结构频率摄动的情况，研究DTMD 的减振效果，结果表明DTMD 能实现与MTMD 接近的效果与鲁棒性。闫维明等[13，14]分析了不同参数对 DTMD 共振峰值和调频宽度的影响，并对地震作用下多自由度结构的DTMD 优化设计方法进行研究。

目前针对输电塔的TMD 风振控制方法缺乏对结构频率摄动的适应性，而对于输电塔上DTMD 的风振控制效果尚未有过研究。本文针对某实际工程输电塔结构，建立加装DTMD 多自由度模型的控制方程，对方程进行拉普拉斯变换并求得受控结构频响函数。针对分别加装DTMD 和TMD 的输电塔结构进行风振控制对比分析。分别考虑结构频率固定与摄动两种情况，提出“单频优化”和“宽频优化”两类减振率优化目标并搜寻阻尼器的最优参数，最后对比分析了不同优化目标下DTMD 与TMD 的减振效果及鲁棒性。

1 控制方程及频域计算方法

对于安装DTMD 的多自由度结构，地震荷载下的结构响应已有推导[14]，以下给出风荷载作用下结构响应的频域计算方法。如图1所示，将DTMD 设置在多自由度结构的第k个质点上，主结构所受外力为{f(t)}，下层TMD 的质量、刚度、阻尼分别为m1、k1、c1，上层 TMD 的质量、刚度、阻尼分别为m2、k2、c2，主结构、质点k、下层TMD、上层 TMD 的位移分别为{x0}、x0k、x1、x2。

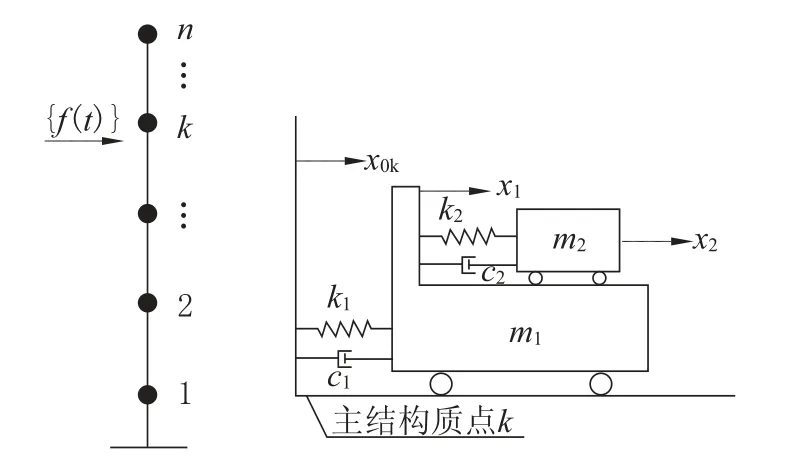
图1 结构-DTMD 理论模型Fig.1 Theoretical model of structure-DTMD system

结构-DTMD 系统运动方程为：

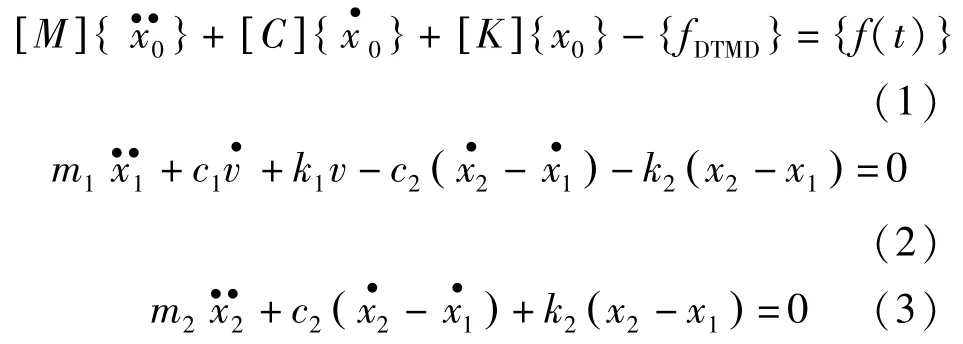
假定DTMD 仅控制结构第一振型，对式(1)～(3)进行Laplace 变换，联立解得结构一阶频响函数为：

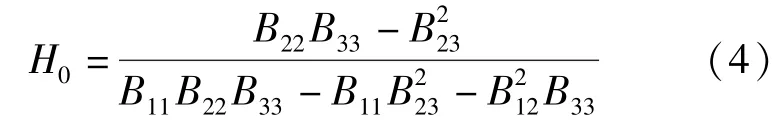
式中：

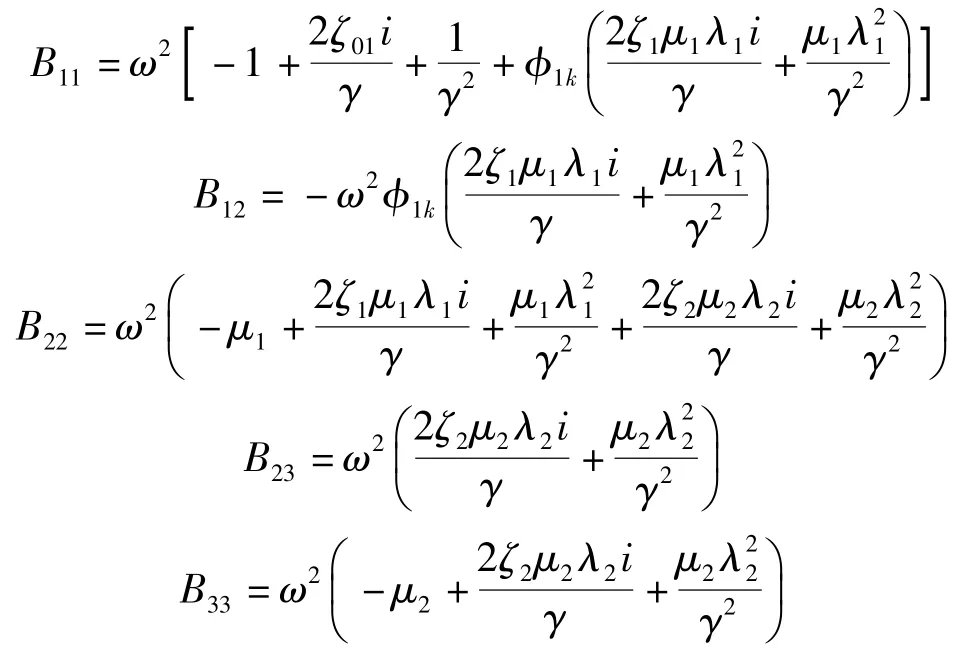
μ1分别为结构一阶模态质量、一阶阻尼比、一阶频率，φ1k为质点k处的一阶振型位移，ω1、ω2分别为下层TMD和上层TMD的自振频率。

对于传统类型的TMD控制下的多自由度结构，其频响函数参见文献[15]。

对输电塔结构所处风场，采用建筑结构荷载规范(GB 50009-2012)[16]规定的B类风场，脉动风速功率谱选用随高度变化的Kaimal谱[17]。输电塔的顺风向风致响应计算流程为[18]：先计算得脉动风速互谱、脉动风压互谱、广义力谱，然后根据各阶模态频响函数、广义力谱求得各阶模态响应均方根，最后通过SRSS方法计算结构响应。

2 阻尼器优化方法

2.1 阻尼器优化目标

定义减振率为：

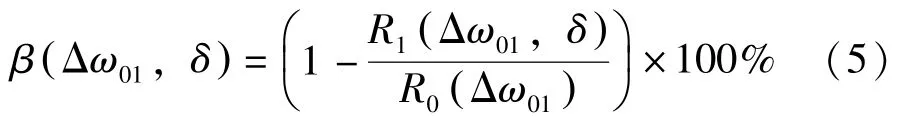
式中：Δω01为结构频率摄动值；δ泛指阻尼器各项可变参数；R1为加装阻尼器的塔顶响应；R0为未加装阻尼器的塔顶响应。塔顶响应可取位移或加速度均方根，本文采用加速度均方根。

定义结构频率未摄动条件下阻尼器能实现的最优减振率：

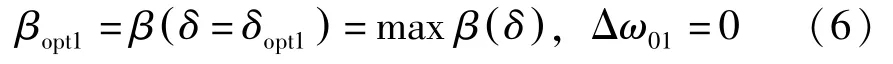
式中：δopt1为阻尼器最优参数。

本文考虑±10%的结构频率摄动范围，在固定阻尼器参数前提下，结构频率摄动区间内最小减振率为：

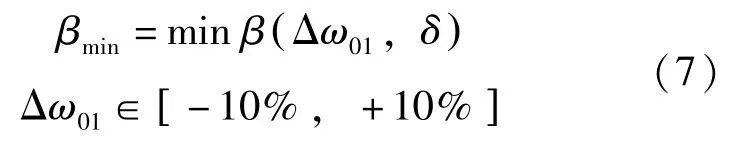
式中：δ为定值。

结构频率摄动范围内，必存在一组最优的阻尼器参数，使得βmin实现最大值，该最大值记为βopt2：

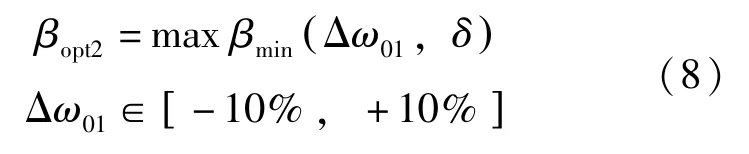
2.2 阻尼器最优参数搜寻方法

以下根据不同的减振率指标提出两类优化目标，利用MATLAB 编写程序分别搜寻阻尼器的最优参数。基于结构频率固定的设定，定义“单频优化目标”为βopt1。基于结构频率摄动的设定，定义“宽频优化目标”为βopt2。

单频优化目标下的阻尼器称为“单频DTMD”和“单频TMD”，宽频优化目标下的阻尼器称为“宽频DTMD”和“宽频 TMD”。其中，单频 TMD即传统类型的TMD，因其基于固定的结构频率进行优化。

定义质量比μ为阻尼器总质量与输电塔一阶模态质量的比值。对于DTMD，其内部两个质量块的相对质量大小也是可变量，故定义下层质量块的质量与DTMD 总质量的比值μ′作为待搜寻的参数：

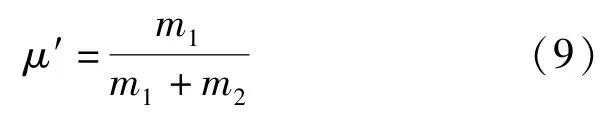
给定结构阻尼比和质量比，在选定的优化目标下，利用程序可对 DTMD 的 5 个参数(λ1，λ2，ζ1，ζ2，μ′)，以及 TMD 的频率比、阻尼比参数(λTMD，ζTMD)分别进行全局最优参数搜寻。

3 输电塔模型的建立

一般而言，随着输电塔高度的增加，输电塔位移响应的共振分量比重增大，从而质量调谐阻尼器可取得更好的控制效果。本文建立的DTMD控制下输电塔响应计算方法适用于任何塔型和塔高，而选用一个高度相对较低的输电塔可检验阻尼器控制效果的下限，即选用其他高度更高的塔时，可预期实现更好的控制效果。本文选用某自立式角钢塔，塔高43.6 m，这种高度的角钢塔在电力工程中较为常见。

3.1 有限元模型

采用beam188 空间梁单元建立输电塔的空间钢材刚架模型，每个杆件划分为1 个单元，全塔共计540 个节点，1386 个单元。弹性模量取E＝2.06×1011N/m2，密度取ρ＝7850kg/m3，泊松比取ν＝0.3。输电塔的三维有限元模型如图2所示，前三阶频率及振型如表1所示。

3.2 多质点模型

为便于频域法计算输电塔响应，建立多质点模型。将输电塔沿竖向分为17 层，每层质量缩聚到层中心质点上。用ANSYS 模型中提取的模态振型和自振频率模拟多质点模型的动力特性。采用瑞利阻尼，令结构X向第一阶和第二阶阻尼比相同。

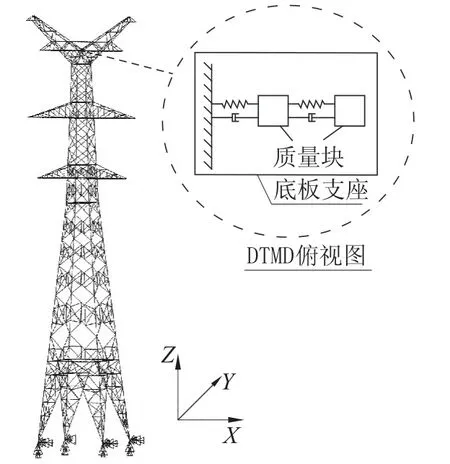
图2 输电塔有限元模型及DTMDFig.2 Finite element model of the transmission tower and DTMD

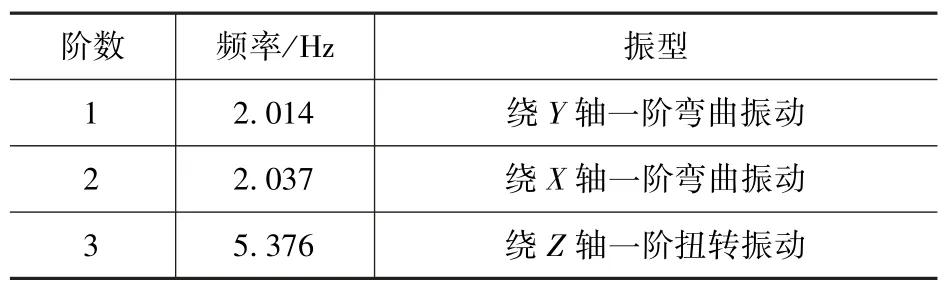
表1 前三阶频率及振型Tab.1 First three natural frequencies and vibration modes

4 数值计算

4.1 计算设置

输电塔X向一阶广义质量为1964kg，若取阻尼器质量比0.02，则阻尼器质量为39.3kg。输电塔顶部空间狭窄，对调谐质量阻尼器的尺寸有限制，可使用专为输电塔设计的小型阻尼器[19，20]。将阻尼器安装在图2塔顶，对应X向归一化振型位移φ1k＝0.84。

对输电塔结构所处风场，取10m 高平均风速为30m/s，来流风向平行于横担方向，且阻尼器运动方向与来流风向平行。取输电塔前10 阶模态计算结构响应，假定阻尼器只控制一阶模态响应，其余阶模态响应不受影响。

以下如未特别说明，默认取结构阻尼比ζ01＝0.01，质量比μ＝0.02。

4.2 阻尼器最优参数搜寻结果

给定8 组不同的结构阻尼比和质量比，在单频优化和宽频优化两种优化目标下，利用程序对DTMD 和TMD 分别进行全局最优参数搜寻，所得结果见表2和表3。由表可知，在各给定参数条件下，单频与宽频DTMD 的ζ1均相当接近0。这是由于搜寻程序中最小精度的限制，实际上ζ1可视为0。另外，由表3可知，随着μ的增大，宽频 DTMD 的ζ2、单频和宽频 TMD 的ζTMD均逐渐增大，而单频和宽频 DTMD 的μ′呈下降趋势。

表2 μ=0.02、不同结构阻尼比条件下的阻尼器最优参数Tab.2 Optimal damper parameters with a mass ratio of 0.02 and different structural damping ratios

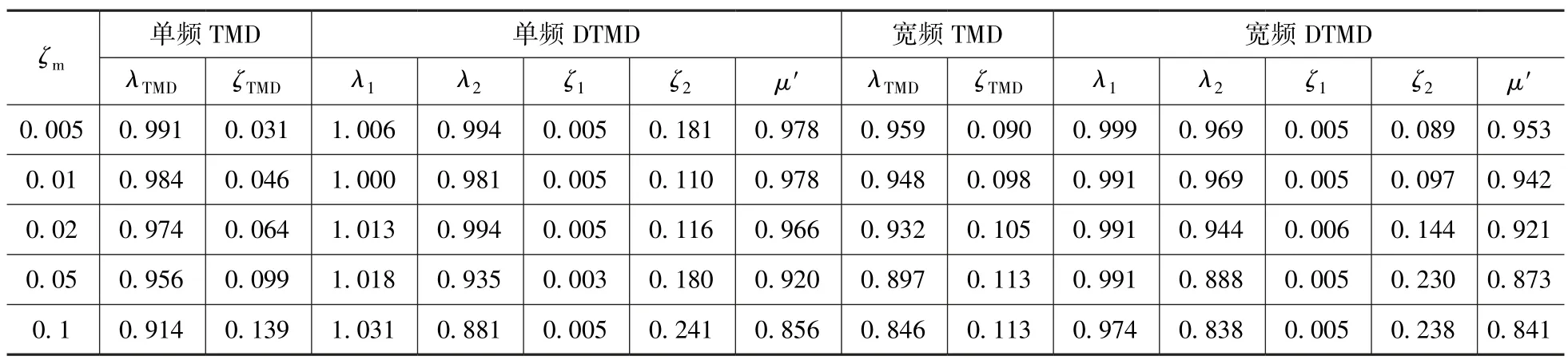
表3 ζ01 =0.01、不同质量比条件下的阻尼器最优参数Tab.3 Optimal damper parameters with a structural damping ratio of 0.01 and different mass ratios

将宽频 DTMD 的λ1及λ2参数、单频 TMD、宽频TMD 的频率比参数沿质量比横轴绘制，如图3所示。由图可知，宽频DTMD 的两个频率比λ1、λ2分别位于单频 TMD 的曲线上下两侧，且λ1与λ2的差值随着μ的增大而增大。这表明在宽频优化目标控制下，DTMD 的两个频率分散到传统类型TMD 最优调谐频率的两侧。此外，宽频TMD 的λTMD曲线比单频TMD 要低，而与宽频DTMD 的λ2较为接近。

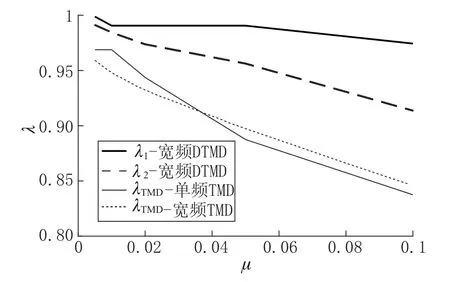
图3 ζ01＝0.01, 各类阻尼器频率比随质量比变化曲线Fig.3 Relation between frequency ratio and mass ratio for different dampers with ζ01＝0.01

4.3 单频优化目标下减振效果分析

基于结构频率固定的设定，对单频优化目标下的优化结果进行分析。

由图4可知，随着μ的增大，单频 DTMD 的最优减振率βopt1持续增大，当μ大于 0.02 时，βopt1增大的趋势变得不明显。因此将μ控制在0.02 以下是较为经济高效的选择。此外，单频DTMD 与 TMD 的βopt1之差维持在 + 0.9%～+1.7% 之间，这表明单频优化目标下DTMD 相对于TMD 减振率的优势对不同质量比条件均成立。

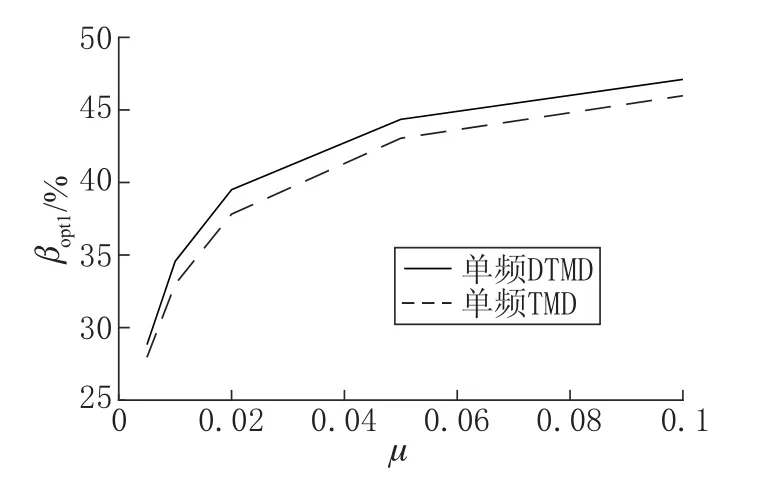
图4 ζ0 1＝0.01, 最优减振率随质量比变化曲线Fig.4 Relation between optimal reduction ratio and mass ratio with ζ0 1＝0.01

由图5可知，随着ζ01的增大，单频 DTMD的最优减振率βopt1持续减小，但单频 DTMD 与TMD 的βopt1之差维持在 +1.2%～ +1.9%之间，这表明单频优化目标下DTMD 相对于TMD 减振率的优势对不同结构阻尼比条件均成立。

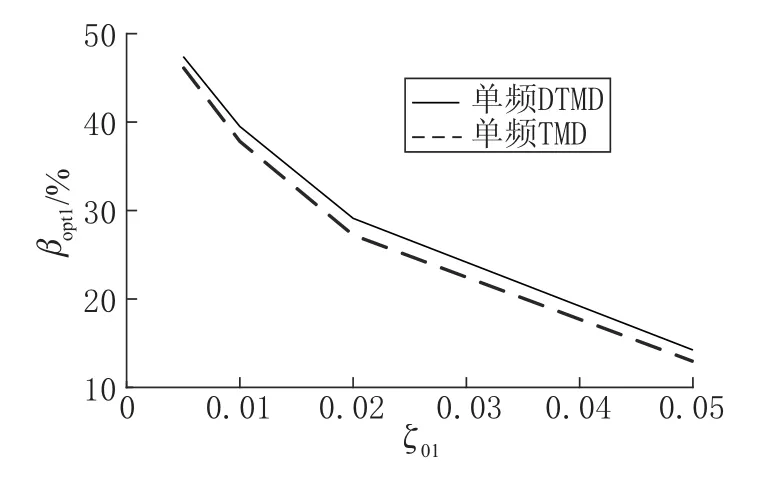
图5 μ＝0.02, 最优减振率随结构阻尼比变化曲线Fig.5 Relation between optimal reduction ratio and structural damping ratio with μ＝0.02

4.4 宽频优化目标下减振效果分析

基于结构频率摄动的设定，搜寻得宽频优化目标下DTMD 和TMD 的最优参数，绘制减振率随结构频率变化的曲线，并将单频优化目标下DTMD 和TMD 的减振率曲线一并绘制进行对比，如图6所示。

图6中，在[-10%，+10%]频率摄动区间内，四种阻尼器的最小减振率βmin由高到低排列，依次为宽频 DTMD 的 32.5%、宽频 TMD 的29.0%、单频 TMD 的 22.6%、单频 DTMD 的20.9%。在结构频率摄动值为0 处，β值由高到低依次为单频 DTMD、单频 TMD、宽频 DTMD、宽频TMD。这表明在区间最小减振率βmin方面，宽频优化目标下的阻尼器比单频优化目标下的阻尼器具有优势，但在原始频率处，宽频优化的阻尼器减振效果有所下降。

图6 四类阻尼器的减振率随结构频率变化曲线Fig.6 Relation between reduction ratio and structural frequency for four types of dampers

由图7和图8可知，在各组结构阻尼比、质量比条件下，依据βopt2指标，各类阻尼器减振效果排序相同，由强到弱依次为宽频DTMD、宽频TMD、单频 TMD、单频 DTMD。

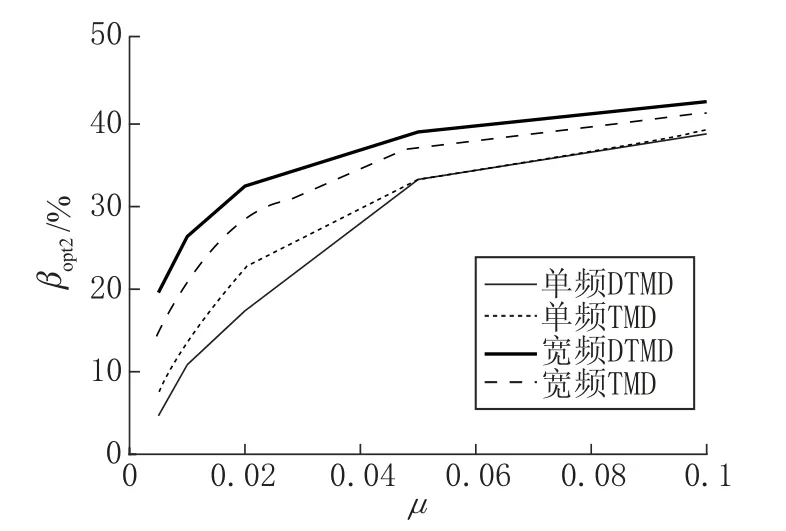
图7 ζ0 1＝0.01, βopt2随质量比变化曲线Fig.7 Relation between βopt2 and mass ratio with ζ0 1＝0.01

由图7可知，随着μ的增大，四类阻尼器的βopt2曲线持续增大，但增大的趋势减缓，其竖向间距逐渐减小。这表明随着μ增大，四类阻尼器逐渐接近其减振效果的极限，且这四者的极限值较为接近。在实际应用中，阻尼器质量不宜过大，μ一般小于 0.02。而在小质量比的条件下，宽频DTMD 相比于其他三类阻尼器的减振效果的优势更为明显。在μ＝0.01 处，宽频 DTMD 与传统类型的单频 TMD 相比，βopt2从 13.9% 提高到26.4%。

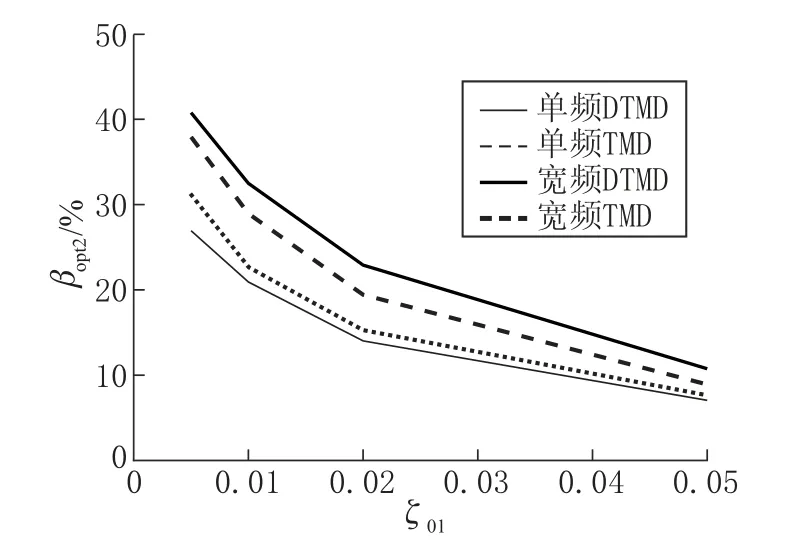
图8 μ＝0.02, βopt2随结构阻尼比变化曲线Fig.8 Relation between βopt2 and structural damping ratio with μ＝0.02

由图8可知，随着ζ01的增大，四类阻尼器的βopt2曲线持续下降，但下降的趋势减缓，其竖向间距逐渐减小。这是由于ζ01增大后，结构响应的共振分量下降，加速度也下降，从而阻尼器的减振效果下降，各类阻尼器之间的βopt2差值亦收窄。在ζ01＝0.01 处，宽频 DTMD 与传统类型的单频TMD 相比，βopt2从22.6%提高到32.5%。

5 结论

本文针对风荷载作用下加装阻尼器的输电塔结构，建立多自由度结构模型并推导了结构-DTMD 系统的频响函数；考虑输电塔结构频率的固定与摄动，根据“单频优化”和“宽频优化”两类优化目标，搜寻得到不同结构阻尼比、质量比条件下阻尼器的最优参数。结论如下：

1.在各组给定条件下，当结构频率摄动时，各类阻尼器减振效果排序相同，由强到弱依次为宽频 DTMD、宽频 TMD、单频 TMD、单频 DTMD。

2.在较小质量比的条件下，基于宽频优化的DTMD 具有明显更强的鲁棒性。μ＝0.01，ζ01＝0.01 时，宽频 DTMD 与单频 TMD 相比，最小减振率的最优值βopt2从13.9%提高到26.4%。

3.综合比较以上四类阻尼器，基于宽频优化目标设计的宽频DTMD 针对结构频率摄动的情况具有较强的鲁棒性，因此对输电塔结构全生命周期的风振控制具有更好的适用性。