单管塔顺风向风荷载的数值模拟与规范对比

张晋元 胡涛

(天津大学建筑工程学院 300350)

引言

在通信铁塔的建设项目中，单管塔由于其造型美观、回转半径大、体型系数小等优点在通信输电设施中被广泛使用。对于单管塔来说，风荷载对其起到绝对的控制作用，主要体现在动力效应上[1，2]。为保证单管通信塔设计的安全性，各国均制定了相应的荷载规范。中国《钢结构单管通信塔技术规程》(CECS 236：2008)[3]是由同济大学主编并于2008年施行的，十年来对于风荷载理论的更深层次研究和各国规范的相继完善，各国规范对脉动效应的计算原理和取值都有了变化，如何合理地对单管塔风荷载标准值进行取值，是目前国内设计人员参与到国际项目设计中面临的主要问题。

徐华刚等通过对美国通信塔计算标准单管塔风荷载计算的介绍，与中国通信单管塔设计规范的计算进行比较，得出两者计算结果的差异[4]。陈俊岭等通过对比分析美国规范、欧洲规范、中国规范中的风荷载计算公式，再通过具体模型的数值模拟，得出了各规范之间风荷载计算的差异[5]。汪大海等以工程实际输电塔为研究对象，通过非线性有限元数值模拟计算，分析了不同情况下风振系数的取值并与国外规范进行对比[6]。

本文根据中国铁塔股份有限公司提供的《通信铁塔标准图集》(Q/ZTT 1002-2015)，选取编号DGT(C)-50-0.65-4PT 型号塔为研究对象，通过MATLB 编制的时程曲线进行非线性数值分析，并将计算的结果与中国《钢结构单管通信塔技术规程》(CECS 236：2008)、美国规范《Structural Standard for Antenna Supporting Structures and Antennas》(TLA-222- G)[7]、欧洲规范《Eurocode 1：Actions on structures—part 1-4：General action—wind actions》(EN 1991-1-4：2005)[8]的计算结果进行对比，为中国《钢结构单管通信塔技术规程》(CECS 236：2008)的修订提供一些客观的参考和借鉴。

1 有限元模型

本算例是一个55m 高的插接式单管通信塔，基本设计资料为：塔主体高度为50m，主体以上为长度5m 的避雷针装置。塔底端的管直径为1.65m，顶端的管直径为0.7m，塔体直径从低处到高处逐渐变小。塔上有4 个平台，间距为5m。上平台离地48m，平台直径均为2.4m，每个平台有 6 副天线，设计资料见图1。钢材均为Q345。

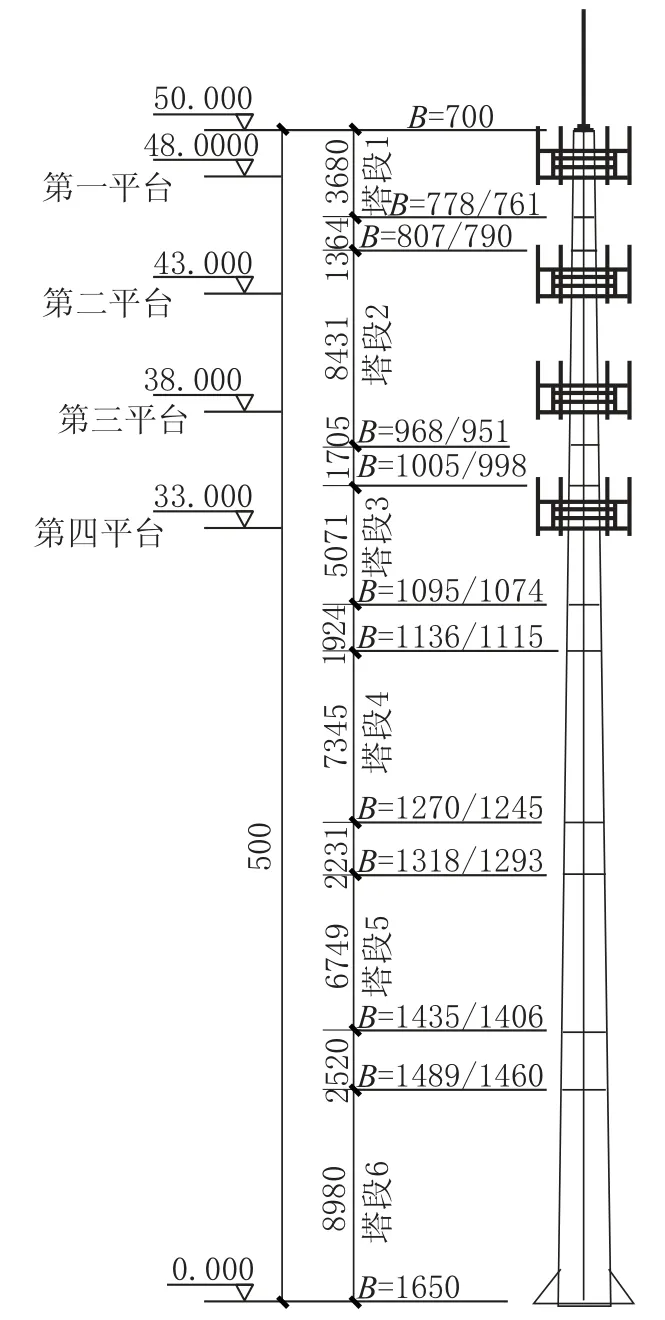
图1 设计资料Fig.1 Design resources

为了提高数值模拟精度的同时提高运算速度，对单管塔模型做了一些处理。内法兰主要起到连接和防止在截面突变处局部弯曲作用，其在水平面内的刚度很大，但是，这对于单管塔的竖向侧向刚度没有多大的贡献，因此在对结构分析时，考虑法兰盘并不能对结构的侧移和弯矩有较明显的贡献[9]，本文在建模中均没有建入内法兰盘，同时忽略了螺栓作用。避雷针由于其迎风面面积很小，对于塔整体风振响应分析意义不大，因此也未建立在整体模型中。

文献[10]指出对于单管塔非线性有限元分析，塔体采用梁单元模型和壳单元模型计算结果差距不大，且梁单元模型简单、方便，故本模型塔体部分选择梁单元模拟。平台部分由于构件较复杂，用实体单元模拟，建立的有限元模型见图2。

本文在对该算例进行脉动风荷载模拟时，将模型离散为10 个质量集聚点(每5m 一个，不考虑避雷针)，即10 个塔段的顶点(图3)。即需要求出质点1～10 的脉动时程曲线。

图2 有限元模型Fig.2 Finite element model

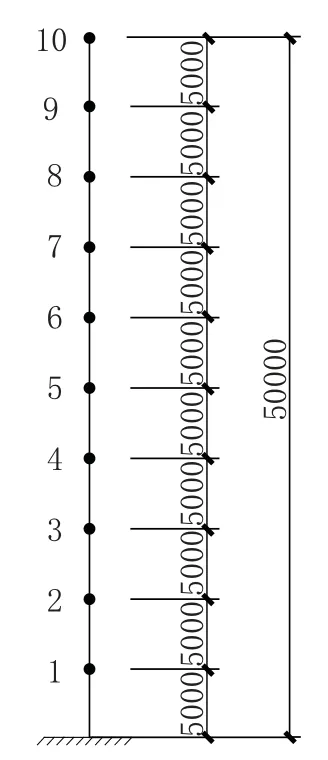
图3 质点模型Fig.3 Particle model

2 风场模拟

作为随机荷载，脉动风需要随机振动理论来描述其变化过程。目前，对于风速时程曲线的模拟方法用的最多的是线性滤波法，包括自回归线性滤波器AR 法(Auto-Regressive Method)和自回归滑动平均线性滤波器法ARMA(Auto-Regressive Moving Method)，而AR 法因其计算速度较快而计算量较小，近些年来被广泛用于求解随机振动问题[11]。

本文采用AR 模型法模拟单管塔风速时程曲线，并将模拟的风谱与目标谱进行对比，以验证模拟风速时程曲线的有效性。

功率谱密度函数反映了某一频域上脉动风的能量分布，其中最具代表性的是Davenport 风速谱[12]。其中Davenport 风谱及参考数值见式(1)：

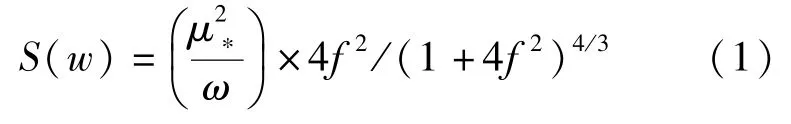
式中：f＝1200ω/V10，V10为10m高度处的平均风速；ω为频率，rad/s；μ∗为剪切波速，μ∗＝kVz/ln(z/z0)，m/s；其中k为卡曼参数，地貌为B类；z0为地面粗糙度常数，z为离地面的高度，m；Vz为z高度处的平均风速，m/s。

样本采集点数为6000，计算阶数P＝4(回归阶数在4阶以上才能得到合理的模拟结果[13])。初始时间t和时间增量dt都为0.1s；初始频率为ω＝0.001Hz；频率增量为Δω＝0.001Hz；截止频率为6Hz；计算时长T＝600s。

由于篇幅原因，图4只给出了3个质点高度处的脉动风速时程曲线。图5给出了50m 高度处脉动风速时程的功率谱密度函数和目标功率谱密度函数的比较。由图可知，仿真风速谱和目标谱基本符合，说明各仿真脉动风速时程随机特性与所需特征吻合。

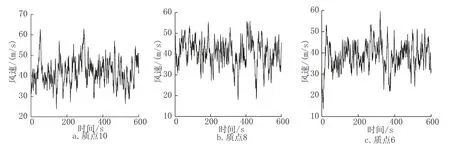
图4 质点10、8、6 处脉动风速时程曲线Fig.4 Pulsating wind speed time history curve at 10，8，and 6

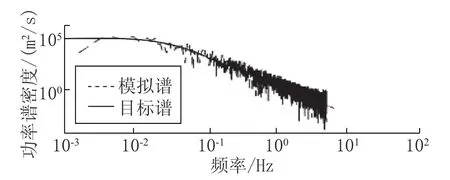
图5 50m 高度脉动风速模拟谱与目标谱比较Fig.5 Comparison of simulated spectrum and target spectrum of pulsating wind speed at 50m height

3 模态分析

本文先进行了塔体结构的动力模态分析，以检验模型的正确性，也为掌握模型塔结构自身的动力特性。图6给出了前2 阶模态分析结果。

由模态分析可以计算出用于动力时程分析所需的阻尼系数。阻尼采用工程中常用的Rayleigh阻尼，将质量与刚度比例阻尼相结合，见式(2)：

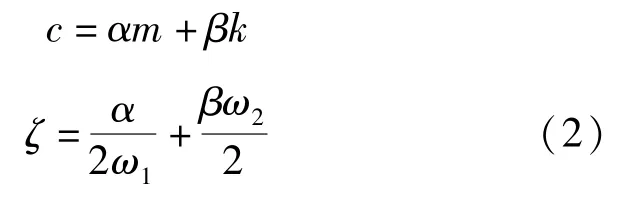
式中：c为阻尼常数；α和β为常数；m和k分别为质量和刚度；ζ为阻尼比；ω1、ω2为自振频率。

由模态分析得到的第一和第二阶圆频率，即ω1＝2πf1＝4.21；ω2＝2πf2＝18.54。根据高耸结构设计规范中对于钢结构单管塔阻尼比可取0.01，因此对于两个振型阻尼比均为0.01。即由式(2)求出α、β为：

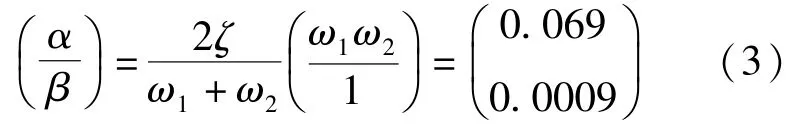
图6 单管塔前两阶模态Fig.6 Two-stage modal diagram of single tube tower

4 风振响应

根据《高耸结构设计规范》 (GB50135-2006)[14]，垂直于高耸结构单位面积上的平均风荷载标准值为：

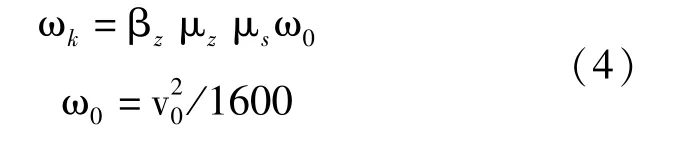
式中：ωk、ω0分别为风荷载标准值、基本风压标准值；μk为 z 高度处风压高度变化系数；μs为体型系数，对于外爬梯的塔体取0.9，平台及栏杆取1.9，通信天线取 1.3；βz为 z 高度处风振系数；v0为基准高度处的风速。

该模型在平台处体型系数较为复杂，为了方便计算，将塔体、平台、通信天线的体型系数根据受风面积合并成一个综合体型系数，见式(5)：

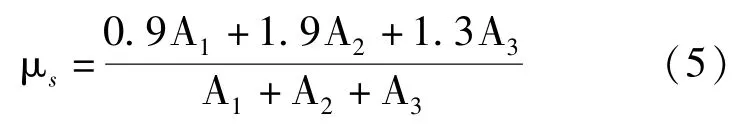
式中：A1表示塔体挡风面积；A2表示平台挡风面积；A3表示天线挡风面积，结果见表1。

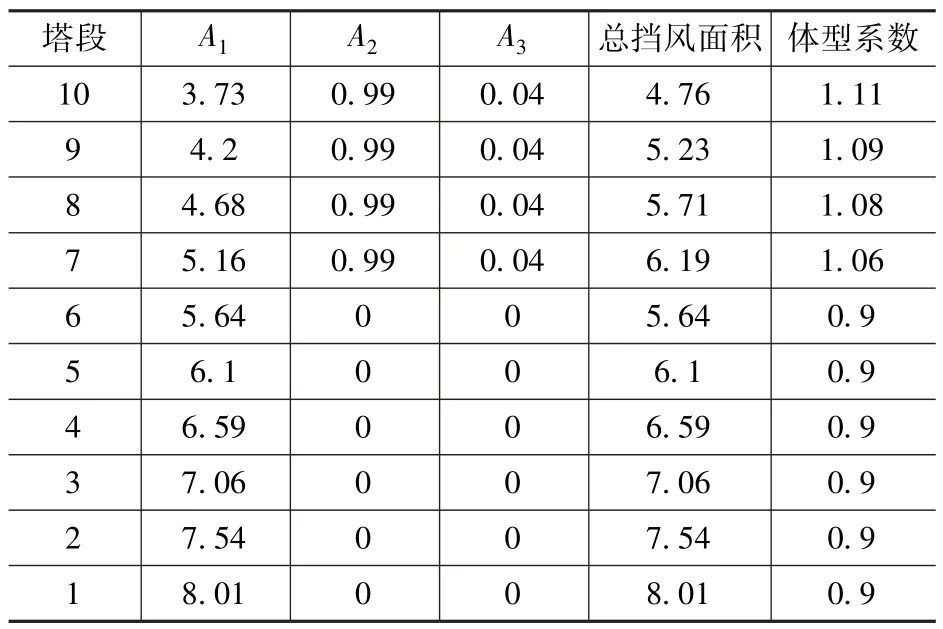
表1 体型系数计算Tab.1 Body shape calculation

由于模拟风速已经考虑了脉动风和风压高度变化系数的变化。因此，根据式(4)求出各个高度处的基本风压后，再乘以式(5)体型系数即可得到风荷载标准值，再由各塔段的挡风面积即可求出作用在各塔段的风荷载值。

将各塔段的风荷载值加载在各段进行动力时程分析，可以得到10 个质点的振动响应(位移响应、加速度响应、基地弯矩响应等)，本文选取位移响应进行比较，由于篇幅原因，只给出了质点9、10 的位移响应曲线(图7)，各个质点位移响应统计见表2。

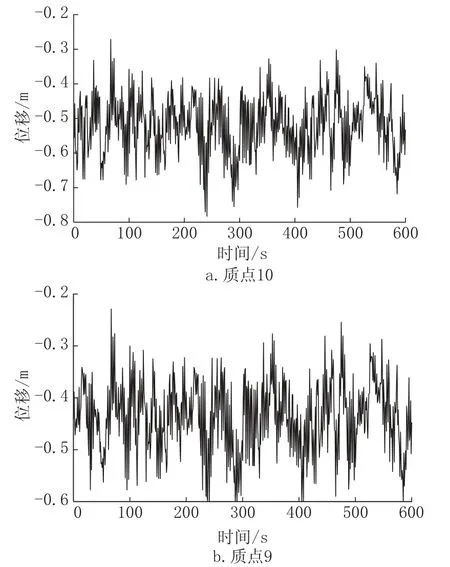
图7 质点9、10 位移响应Fig.7 Displacement response of particle 9、10

表2 位移响应统计Tab.2 Displacement response statistics

对于高耸塔体结构，其第一阶振型对风振响应起主要作用，且只考虑第一阶振型，可由式(6)计算风振系数[15]：

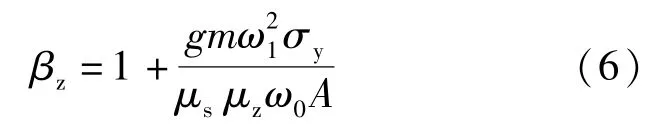
式中：g为峰值因子，取 2.5；m为质量；ω1为第一阶自振圆频率；σy为单管塔顺风向位移均方差；A为迎风面面积；μs、μz、ω0、βz等物理量与式(4)中一致。

由以上信息可以计算单管塔各高度处风振系数及风压值，见表3。

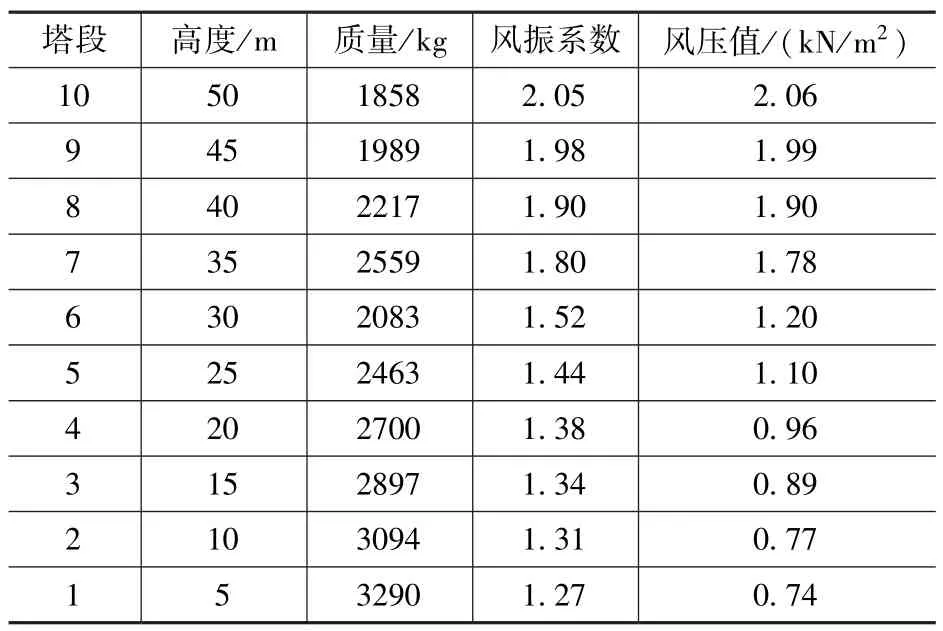
表3 风振系数及风压值Tab.3 Wind vibration coefficient and wind pressure standard value

5 各国规范风荷载标准值及位移响应

由于各国国情不同，规范中定义的平均风剖面不一样，为了便于比较，选取各国标准地貌条件，即与我国荷载规范中的B 类开阔田野地貌条件相对应。TLA-222-G 标准选取C 类地貌条件，EN 1991-1-4：2005 规范选取Ⅱ类地貌条件。

5.1 美国TLA-222-G行业标准

TIA-222-G 标准(以下简称美国规范)对于通讯塔结构及附件的计算给出了详尽的计算公式和说明，在美国乃至世界各国得到广泛应用。

TLA-222-G 标准中风荷载计算公式为：

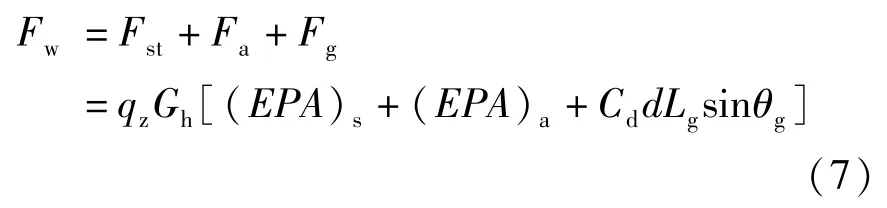
式中：Fst为支撑结构所受风力；Fa为附件，如平台、天线支架等所受风力；Fg为拉线所受风力；qz为高度处的速度压力；Gh为阵风系数；(EPA)s及(EPA)a分别为结构及附件有效迎风面积；Cd为拉线体型系数；d为拉线直径；Lg为拉线长度；θg为拉线与风向之间的夹角。

根据规范计算可得到C 类地貌条件下，模型不同高度处的风压值和位移值见表4。

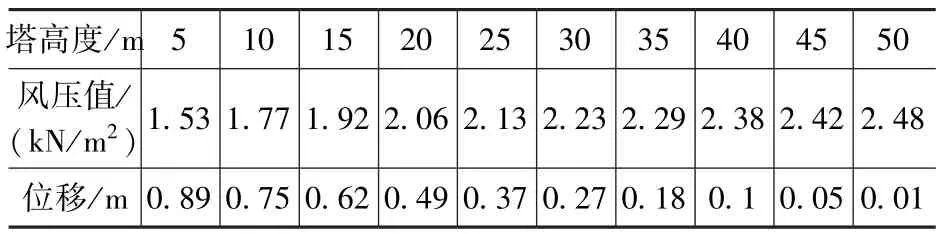
表4 美国规范单管塔各高度处风压值及荷载响应Tab.4 Wind pressure and load response at various heights of single-tube towers in the United States

5.2 欧洲EN1991-1-4:2005国家规范

欧洲规范是一套适用于欧洲大部分地区的通用型建筑规范，其中EN 1991-1-4:2005(以下简称欧洲规范)适用于高度200m 以内的建筑和土木工程结构、跨度不超过200m 的桥梁。对于高耸结构的风作用按式(8)计算：

式中：cscd为结构系数，是尺寸系数cs和动力系数cd的乘积；cf是结构整体或构件的力系数；qp(ze)是参考高度ze处的峰值速度压力；Aref是基准面积。

根据规范计算可得到Ⅱ类地貌条件下，模型不同高度处的风压值和位移值见表5。

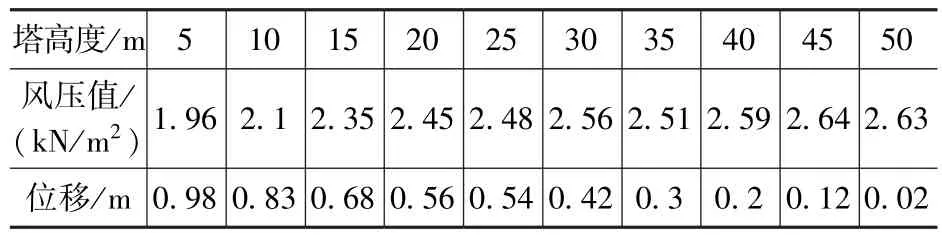
表5 欧洲规范单管塔各高度处风压值及荷载响应Tab.5 Wind pressure and load response at various heights of single-tube towers in Europe

5.3 中国CECS236：2008技术规程

CECS 236:2008(以下简称中国规范)由中国工程建设标准化协会发布，其规定作用于单管塔表面单位投影面积上的水平风荷载标准值应按下式计算：

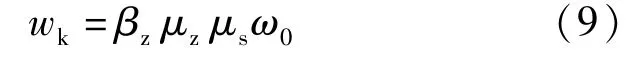
式中：wk为作用在单管塔z高度处单位投影面积上的风荷载标准值；ω0为基本风压；βz为z高度处风振系数；μz为z高度处风压高度变化系数；μs为体型系数。

根据规范计算可得到B 类地貌条件下，模型不同高度处的风压值和位移值见表6。

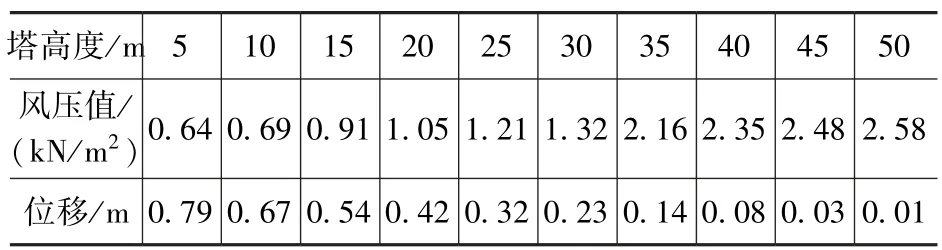
表6 中国规范单管塔风振系数取值Tab.6 Wind vibration coefficient value of single-tube tower in Chinese standard

6 规范比较分析

各规范风压设计值、位移响应对比及其数值模拟结果见图8、图9。可以看出：上部1/4塔段中国规范计算风压值与欧美规范相近；下部3/5 塔段，欧美规范风压值约是中国规范的1.5～2.5 倍，但中国规范涨幅远大于欧美规范；三者都大于数值模拟结果，其中下部1/5塔段，中国规范风压值小于数值模拟结果，偏于不安全。塔身在风荷载作用下的位移：欧洲规范大约是中国规范的1.24 倍，美国规范大约是中国规范的1.13 倍，三者都远大于数值模拟结果，且塔顶位移小于塔高的1/50，在安全的范围内。

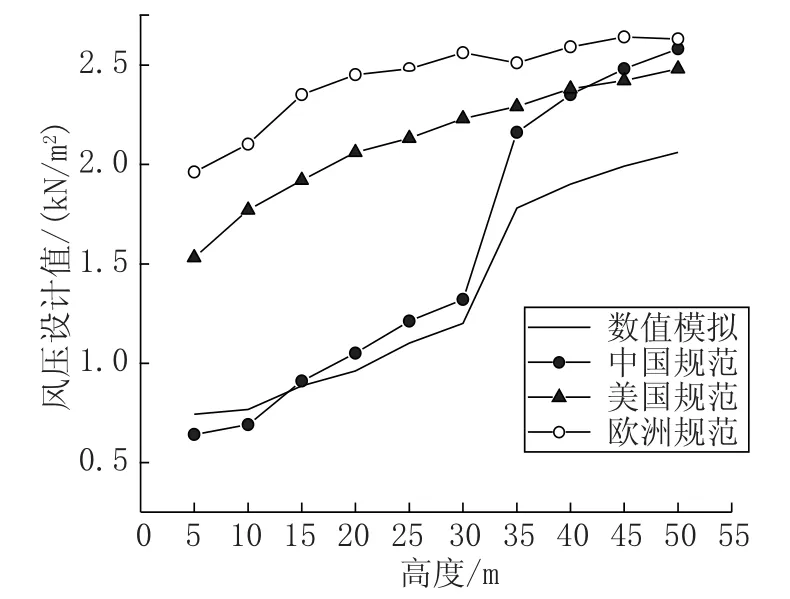
图8 风压设计值对比Fig.8 Wind pressure design value comparison

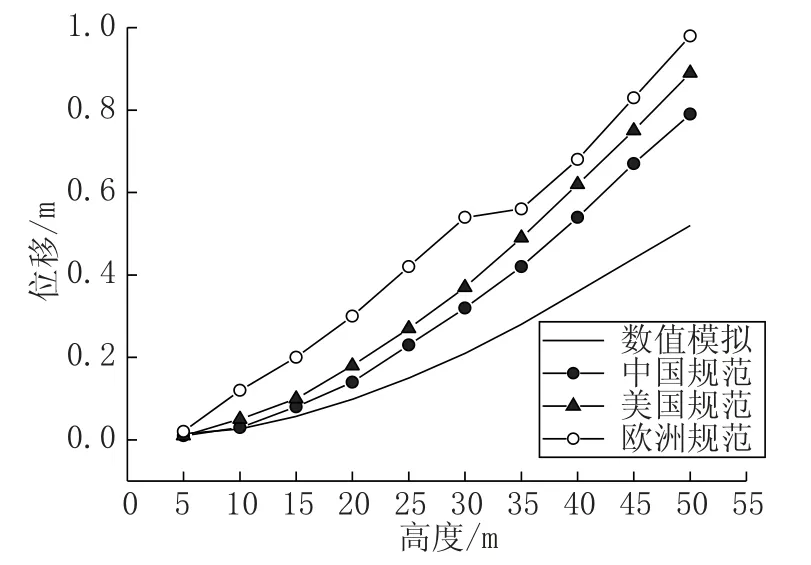
图9 位移响应对比Fig.9 Displacement response comparison

7 结语

本文以实际单管塔结构作为研究对象，基于准常定动力假设，在模拟的风场环境下进行动力时程非线性有限元分析，获得了实际情况下的风荷载并与各国规范进行对比，得出了如下结论：

(1)欧美规范在塔段低处(低于30m)风荷载值远大于中国规范，且管塔结构设计主要由风荷载、位移等因素控制，可见欧美规范对低矮管塔在强度方面比我国规范稍有富余。

(2)中国规范对于高度大于40m 的单管塔，风荷载值偏大，偏于保守。而在高度较低处，中国规范给出的风荷载小于数值模拟得到的结果，缺乏安全性。

另外，对于高宽比较大的圆形截面高耸建筑应当考虑其横风向风振的影响，本文由于限于篇幅和主题不再展开讨论，有待做进一步研究和分析。