正八边形钢板腹梁弯曲性能试验研究

常山 杨明 田林杰 袁鹏飞

(1.东南大学交通学院 南京211189；2.中设设计集团交通设计研究院 南京210004)

引言

蜂窝钢梁是一种较早被人们使用的钢结构，广泛用在高层建筑和展览馆等大跨度结构中[1]。国外对蜂窝钢梁的应用和研究起步较早，在20世纪50年代就出现了挠度的简化计算方法，其中就包括目前最为重要的费式空腹桁架法。1984年，Evans 和Shanmugant[2]提出了一种用于分析蜂窝结构线性和非线性极限承载力的简化分析方法；1991年，Knowles[3]等对蜂窝钢梁的承载能力和挠度计算方法进行了具体分析；2006年，Zirakian 和Showkati[4]为研究蜂窝钢梁的畸变屈曲，进行了六支足尺蜂窝钢梁的试验研究；2011年，Gholizadeh[5]等研究了简支蜂窝钢梁腹板屈曲承载能力，讨论了非线性有限元方法评估梁承载能力和破坏模式的准确性；2011年，Sweedan[6]等采用有限元方法分析了蜂窝梁构件腹板弹性局部屈曲的临界荷载。

我国在20世纪50～70年代，因限制使用钢结构，只有少数冶金企业少量地应用过蜂窝梁[7]。1993年，苏益声和王良才[8]对圆孔蜂窝梁的制作工艺进行了介绍，并基于费氏空腹桁架理论，提出了圆孔蜂窝梁的强度简化计算法。2017年，廖曙波和罗烈[9]通过 MATLAB 数学工具实现了积分运算基本表达式计算圆孔蜂窝梁的挠度，该基本表达式基于费式空腹桁架理论得到。2015年，王培军[10]等提出了一种圆角多边形孔蜂窝梁孔间腹板受剪屈曲承载力的分析方法，研究了跨中集中力作用下的蜂窝梁孔间腹板的屈曲模式和屈曲承载力。

目前对蜂窝钢梁的研究主要集中在挠度计算、极限承载力研究和腹板侧向扭转屈曲等方面。从蜂窝钢梁的研究方向可以看出，蜂窝钢梁的腹板抵抗横向扭转变形能力较差，结构整体稳定性较差，这限制了其在桥梁领域的使用。

本文的工作是基于蜂窝钢梁外观，提出了一种腹板稳定性较好、便于工厂化施工和快速安装的钢结构桥梁。正八边形钢板腹梁是一种新型空腹式钢结构主梁，可用作应急桥梁、人行天桥、景观廊桥以及大型桥梁工程的上部结构。该结构采用一系列带孔洞的正八边形钢板形成腹部结构，再通过高强螺栓与顶底板连接形成主梁(图1)。

图1 正八边形钢板腹梁示意Fig.1 Diagram of steel octagon-web beam

与传统的钢结构相比，该结构具有以下特点：首先，工厂预制。结构中所有部件均可采用工厂预制的方式加工制造，可最大限度地保证构件的制作质量；其次，连接可靠。结构中各部件依靠高强螺栓连接，不需现场焊接作业，不仅极大地减少人工作业难度，还可有效保证连接的可靠性；再次，更换方便。当结构中某部件出现破损时，只需要更换破损部件，不需要长时间占用交通；最后，安装方便。由于工厂预制构件并采用高强螺栓连接，将结构各部件运输到架设地段后，可快速进行拼装连接，不需要长期封闭交通。

因此，对正八边形钢板腹梁的弯曲性能进行理论和试验研究，不仅具有理论意义，还可为其应用到工程实践提供技术支持。

图2 正八边形钢板腹梁挠度计算单元示意Fig.2 Diagram of deflection calculation unit for steel octagon-web beam

1 弯曲荷载作用下的挠度计算

正八边形钢板腹梁为腹板非连续的空腹式结构，可借鉴费氏空腹桁架比拟法对弯曲荷载作用下该结构产生的挠度进行计算。将正八边形钢板腹梁的挠度看成弯曲挠度fM、剪切挠度fV和剪力次弯矩引起的挠度fVM三项之和，即f＝fM+fV+fVM，在进行结构挠度计算时，将结构沿梁长划分为多个单元，对单元进行挠度计算，再通过单元挠度叠加得到结构整体挠度。

假设正八边形钢板腹梁圆形开孔部分截面的等效惯性矩为I1，梁墩部分截面的等效惯性矩为I0(只考虑顶底板形成的截面惯性矩)。则正八边形钢板腹梁截面刚度可以表示为EI(x)，式中η为变量，其中圆形开孔部分的截面其他部分截面η＝0 。

根据单位荷载法，正八边形钢板腹梁的弯曲挠度计算公式为：

正八边形钢板腹梁的剪力挠度计算公式为：

正八边形钢板腹梁在剪力次弯矩影响下的挠度fVM，可以采用单位荷载法进行计算。计算时可以将该挠度看作两部分：一部分是剪力作用下的弯曲变形另一部分是梁墩的转动变形则正八边形钢板腹梁的挠度计算公式为：

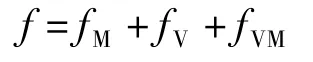
以某高跨比1/10 的正八边形钢板腹梁为例，采用 Q235 钢材制作，弹性模量 210GPa。梁长0.89m，梁宽0.2m。沿梁横向设置两道正八边形钢腹板，正八边形钢腹板圆孔直径为0.04m，所有构件厚度均为3mm。梁左端为固定约束，右端为自由约束，在自由端施加1000N 竖向集中力。按照正八边形钢板腹梁的挠度计算公式可得，该结构的挠度

为验证该公式计算准确性，采用通用有限元软件ABAQUS 2017 建立该正八边形钢板腹梁的有限元模型，采用四节点曲壳缩减积分单元S4R进行网格划分，得到该结构的挠度为5.153×10-4 m。与计算公式值相比，两者误差为2.64%，说明基于费氏空腹桁架理论的挠度计算公式可以准确地计算该结构挠度。

图3 正八边形钢板腹梁挠度(单位：m)Fig.3 Deflection of steel octagon-web beam (unit：m)

2 弯曲性能试验

2.1 缩尺模型试件

根据规范[11]要求，设计了1 根正八边形钢板腹梁缩尺模型试件，图4所示为正八边形钢板腹梁顶板平面尺寸。图5所示为正八边形钢板腹梁的工厂制作。该试件采用Q235 钢材制作，长5000mm，宽 800mm，高 308mm，高跨比 1/15。正八边形钢腹板高300mm，边长124.26mm，中间圆孔直径140mm；横向相邻的两个正八边形钢腹板采用预留有高强螺栓孔道的4 块钢板焊接形成腹部结构单元；顶板底面焊接高40mm、厚4mm、纵向间距 300mm、横向间距 200mm 的加劲肋；顶、底板预留有高强螺栓孔道，且顶、底板两端采用焊接方式连接端部结构；试件两个端部结构为空腹构件，其内部沿横向布置两道等高加劲肋；相邻的腹部结构单元、腹部结构单元与顶、底板的连接均采用8.8 级高强螺栓。所有构件的厚度均为4mm。为防止顶板边缘在较小荷载作用下出现局部失稳，在顶板边缘沿梁长方向焊接厚4mm 的三角形钢连接件，三角形钢连接件与顶板和正八边形钢腹板均为焊接连接。

图4 正八边形钢板腹梁顶板平面示意 (单位：mm)Fig.4 Plan of top slab (unit：mm)

图5 正八边形钢板腹梁制作Fig.5 Manufacture of steel octagon-web beam

2.2 试验加载方式与测点布置

图6所示为试验装置布置，试验采用跨中对称两点加载方式，两个加载点间距1.2 m。加载采用油压千斤顶和反力架设备，施加的荷载大小通过压力传感器测量，油压千斤顶施加的荷载通过分配梁传递给试验梁加载点上部的垫梁。垫梁长度与试验梁宽度一致，采用填埋细砂的方式消除垫梁与试验梁之间的空隙，使得试验梁受力均匀。为检查加载装置和测试仪表的工作状态、各个设备的安全性和可靠性，消除焊接产生的残余应力，先对试件进行预加载，然后卸载。采用分级加载方式，加载过程从零开始逐步递增。

图6 试验装置Fig.6 Setup of test equipment

试验采用TDS-303 静态应变测试仪测量顶、底板在加载位置处和跨中的应变，并在跨中及靠近支点处放置位移计记录挠度。试验梁两端设置为滑动铰支座。

先对试验梁施加30kN 预加载，然后卸载至零。之后采用分级加载的方式进行加载。在加载0～150kN 时，每级加载 30kN；加载超过 150kN后，每级加载10kN，直到试件破坏。

2.3 试验现象

图7所示为试验梁荷载-挠度曲线，由该曲线可以将试验加载过程大致分为三个阶段，各阶级试验现象及规律如下：

第I 阶段(加载小于90.22kN)，试件处于弹性变形阶段，荷载和挠度关系基本为直线。

第 II 阶段(加载在 90.22～ 179.78kN 之间)，荷载和挠度关系近似为直线。试验的挠度随着加载的增加而不断增大。当加载到179.78kN 时，试件跨中的挠度达到17.1mm。

第 III 阶段(加载在 179.78～ 236.50kN 之间)，荷载和挠度关系为曲线。在加载到约183kN 时，试件产生较大异响，此时在两个加载点之间的顶板出现轻微的局部屈曲现象。

在加载超过第III 阶段后，油压千斤顶不能继续加载，挠度变化十分剧烈，认为试件已经处于破坏状态，停止加载。图8所示为试验梁的破坏形式。顶板在加载位置处出现明显的屈曲现象，加载点处的正八边形钢腹板也出现较为明显的屈曲现象。

图7 试验梁荷载-挠度曲线Fig.7 The load-deflection curve of specimen

图8 试验梁的破坏形式Fig.8 The failure phenomena of specimen

3 有限元分析结果

基于通用有限元软件ABAQUS 2017 建立试验梁的非线性有限元分析模型(图9)。试验梁中所有构件均采用S4R 单元进行网格划分，共划分18718 个单元。S4R 是一个四节点线性缩减积分壳单元，该单元适用于较大的应变和应变梯度，特别适用于三维空间问题。模型中采用tie 约束来模拟焊接和高强螺栓连接。有限元模型中建立了四个参考点，其中RP1 和RP4 分别模拟油压千斤顶加载，RP2 和RP3 模拟支座约束作用，参考点与顶板加载部分及端部建立coupling 机动耦合方式，试验梁采用简支约束。

图9 基于有限元软件ABAQUS2017 的试验梁模型Fig.9 A nonlinear finite element model realized by ABAQUS 2017

3.1 荷载-挠度曲线对比

图10为试验和有限元模拟得到的试验梁荷载-挠度曲线。从图10可以看出，试验和有限元得到的荷载-挠度曲线两者基本吻合，尤其在加载初期，两者曲线基本重合。试验得到的结构最大承载力为236.50kN，对应的挠度为27.3mm；有限元模拟得到的结构最大承载力为243.55kN，对应的挠度为31.5mm。试验过程中，试验梁在加载达到236.50kN 之后，由于顶板屈曲较为严重，导致结构在接近其极限承载力后，迅速失效。从两者的荷载-挠度曲线可以看出，有限元模拟结果与试验结果吻合度较好，说明该试验梁有限元模型具有较好的可信度。表1为试验梁加载过程中实测挠度与理论计算挠度值的对比。从表1可以看出，在试验梁处于弹性变形阶段(即加载值小于90.22kN)时，理论计算挠度与实测挠度最大误差小于4.3%，说明提出的挠度计算方法是准确的。当试验梁加载值达到119.70kN 时，试验梁已经进入弹塑性工作状态，因此理论计算挠度与实测挠度差距较大，误差达到了8.9%。

图10 试验和有限元模拟得到的荷载-挠度曲线对比Fig.10 Comparison of load-deflection curves obtained by test and FEA

表1 试验梁加载过程中实测挠度与理论计算挠度值Tab.1 The mid-span deflections of the test specimen under different loads

3.2 应变结果对比

图11为试验和有限元得到的顶、底板在跨中和加载位置处的荷载- 应变曲线。从图11a、11b 和11d 可以看出，试验和有限元模拟得到的顶、底板跨中处的荷载-应变曲线以及底板对应顶板加载处的荷载-应变曲线整体吻合度较好。图11c 所示的顶板加载位置处的荷载-应变曲线变化趋势一致。随着荷载的逐渐增加，顶板加载处由受压转换为受拉，这反映出顶板加载位置处在加载初期顶板为受压状态，而随着加载的不断增大，顶板在两点加载处出现局部屈曲现象，导致该处的应变状态由受压转为受拉。当试验梁达到最大压应力时，有限元模拟得到最大压应变为-441.82με，对应的加载值为 146.94kN，试验得到最大压应变为-517.50με，对应的荷载值为148.23kN，两者得到的加载值接近一致。

图11 试验和有限元模拟得到的荷载-应变曲线对比Fig.11 Comparison of load-strain curves obtained by test and FEA

3.3 应力分布

图12所示为试验梁达到极限承载力时对应的应力分布。从图12可以看出，当试验梁加载到其极限承载能力时，顶板加载处的应力最大，最大应力达到了350MPa 左右。顶板在中间纯弯段处的应力值大部分处在200MPa 左右，底板在中间纯弯段处的应力值大部分处在210MPa 左右，顶、底板应力均超过了Q235 钢材的设计强度。若忽略试验梁腹板的作用，由顶、底板的应力值可以算出试验梁可承受的极限荷载约为240kN，与试验得到的最大加载值236.50kN 较为接近。

在加载点与支座之间的正八边形钢腹板整体受力较小，大部分应力小于100MPa，而在加载点附近的正八边形钢腹板受力较大，最大应力达到了300MPa，大部分应力处在150MPa 左右。

由应力分布结果可以看出，试验梁在加载到极限荷载时，顶、底板应力均达到了Q235 钢材的设计强度值，加载点附近的正八边形钢腹板应力也达到了较大的水平。

图12 极限荷载对应的试验梁应力分布(单位：Pa)Fig.12 Diagram for stress distribution of test specimen under ultimate load (unit：Pa)

4 结论

基于蜂窝钢梁的外观，结合钢圆环腹梁的设计，提出了一种新型空腹钢结构主梁——正八边形钢板腹梁。借鉴蜂窝钢梁的经典挠度计算理论，提出了正八边形钢板腹梁的挠度计算方法，结合规范设计了1 根正八边形钢板腹梁缩尺模型试件，并进行了静载弯曲试验，得到以下结论：

1.基于费氏空腹桁架理论，提出了计算正八边形钢板腹梁的挠度计算方法。通过与有限元方法验证，证实了提出的挠度计算方法是可行的。

2.通过对试验梁进行的静载弯曲试验，得到了正八边形钢板腹梁的破坏形态，顶板在纯弯段区域出现了局部屈曲现象，两加载点位置处的正八边形钢腹板也出现屈曲现象。

3.通过对比试验与有限元模拟得到的荷载-挠度曲线、荷载-应变曲线可以发现，有限元模拟结果与试验结果吻合度较好，说明建立的试验梁非线性有限元模型具有较好的可信度。试验梁静载弯曲试验得到的结构最大承载力为236.50kN，略小于有限元模拟得到的结构极限承载能力值243.55kN。

4.结合试验梁的静载弯曲试验与有限元模拟结果可以发现，正八边形钢板腹梁在达到极限承载力时，顶、底板的应力均超过了Q235 钢材的设计强度，说明该结构具有较好的抗弯性能。