均布荷载作用下等截面连续梁最佳支座布置研究及工程应用

文锋 乔海文

(上海电力设计院有限公司 200025)

引言

连续梁是工程中常用的梁结构，常见诸连续梁桥、单向板、主梁、次梁楼板结构及钢结构中，很多情况下，其计算模型可简化为均布荷载作用下的连续梁模型。对于等截面连续梁而言，特别是对称配筋混凝土梁和钢梁，许多情况下控制梁截面大小的往往是梁内最大弯矩，对于此类问题，如何减小梁内最大弯矩从而减小梁截面和材料用量，是工程中十分关心的问题。

在给定均布荷载大小及连续梁总长条件下，等截面连续梁内最大弯矩只与支座的布置位置相关，改变梁支座间位置可以调整连续梁内弯矩，通过寻找支座较佳的布置位置以优化连续梁内弯矩，例如在桥梁工程中，如何确定大桥的桥墩位置，使得桥梁内力分布合理，从而减小梁截面。

已有相关的研究一般与连续桥梁相关，连续梁桥两端一般无悬挑，其中间跨度(l)相等，两边跨度(l1)略小于中间跨度，以防止边跨支座处负弯矩过大[1]，边跨跨度与中间跨度比被称为边中跨跨径比α(l1/l)，一般认为α应该取值0.5～0.8，此时连续梁桥内力分布较优[2-8]；有文献[9]基于连续梁内弯矩绝对值最小的原则，分析了三跨无悬挑连续梁在均布作用下的最佳支座布置，认为跨径比α＝7/6 时梁内弯矩绝对值最小，但仅分析了三跨无悬挑连续梁，未讨论其他跨度连续梁的优化布置；也有文献[10]从连续梁每个截面正负弯矩绝对值之和最小为原则，分析了2～10 跨无悬挑连续梁在均布荷载及集中荷载作用下的最佳支座布置，分析结果表明，边跨比取0.8 时连续梁内正负弯矩绝对值之和最小。以上有关连续梁跨度确定的研究中，研究对象均为无悬挑连续梁，对于两端有悬挑连续梁的最佳支座布置并未讨论，且讨论中较少以连续梁内弯矩绝对值最小为目标，而文献[9]中仅考虑跨数N＝3 时的跨径比，当跨数不为3 时无法应用。

本文将进一步分析连续梁在跨数N＝1～7 时最大弯矩最小的支座布置，将分四种布置条件进行讨论：(1)两端带悬挑，连续梁支座可随意布置；(2)两端带悬挑，连续梁跨中支座等间距布置；(3)两端无悬挑，连续梁支座可随意布置；(4)两端无悬挑，连续梁支座等间距布置。

通过分析以上四种布置条件下梁内最大弯矩绝对值最小的支座布置规律，给出相应跨度的优化布置方案；并对同跨数条件下四种方案进行对比，分析其差异随着跨数的变化，最后归纳出多跨带悬挑等跨连续梁的优化布置规律。

1 连续梁最佳弯矩分析方法

在弯矩绝对值最小原则下连续梁最佳支座布置，对于给定梁长和支座数的连续梁，确定弯矩最小的支座布置方案，需要同时考虑连续梁弯矩求解方法以及最佳支座布置的搜寻，实际上两者相互影响，选择分析方法时应将二者结合起来考虑。

1.1 连续梁弯矩求解方法

连续梁内弯矩绝对值最小条件下的支座布置，必须进行连续梁弯矩计算，荷载作用下连续梁内弯矩的计算方法有多种，较传统的方法是力法和矩阵位移法，分别属于解析方法和数值方法，这两种方法各有特点，跨数较少时可采用力法直接求解，而当支座较多时或梁上荷载较复杂时，采用数值法效率更高。三弯矩法是一种基于力法的改进方法，通过选择不同的基本结构，确保方程组中每个方程仅含有3 个未知量，方程组系数矩阵为每行仅有三个未知量的稀疏矩阵。

本文拟研究跨数最大为7 的连续梁内弯矩，一共8 个支座，超静定次数为6 次，如果采用力法，则当N＝7 时，6 个支座反力未知量求解需6个方程，方程中系数计算复杂，因此直接选择力法求解是困难的；若采用矩阵位移法或三弯矩法，求解弯矩则相对较为方便。

1.2 最佳支座搜寻

多跨连续梁计算简图如图1所示，梁总长度L和均布荷载q已知，N跨待定跨度变量数为N+1 个，当跨数分别为 1～7 时，对应的独立未知跨度变量数分别为2～8 个，对于无悬挑连续梁，即t1＝t2＝0。

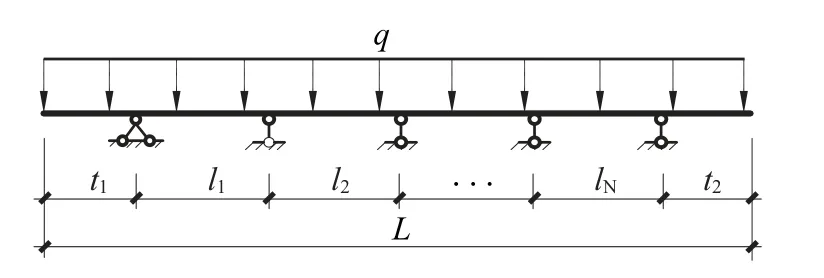
图1 带悬挑连续梁计算简图Fig.1 Sketch of continuous beam with overhang

为寻找多跨连续梁弯矩最小的最佳支座位置，须通过组合各跨不同跨度并计算、比较连续梁内最大弯矩，找到使连续梁弯矩绝对值最小的支座布置，工作量较大。

以7 跨连续梁为例，由于每跨跨度均无约束，一共有8 个待定跨度。无论是采用力法、矩阵位移法还是三弯矩法，8 个待定跨度，编程进行最佳支座布置搜寻时，需要8 层循环嵌套，假设每跨跨度取100 个不同的值，则一共需要对(100)8＝1016个连续梁进行分析计，计算量太大，计算效率将非常低。

1.3 本文求解思路

为避免当跨数较多时搜寻最佳支座布置效率低的问题，在寻找最佳支座布置时，首先采用力法分析跨数N＝1～4 时最佳连续梁的跨度规律。

由于力法属于常用方法，一般结构力学教材中均有详述，其计算原理此处不再赘述。对于任一种支座间距布置，根据力法求得梁各跨跨中及支座处弯矩后，进而求得支座反力和梁中任意位置的剪力，梁中剪力为零处即为可能的弯矩最大处，对比即可求出这一支座布置条件下的最大弯矩值，按照同样的方法，改变支座间距，求解各种支座布置时连续梁内最大弯矩值，并找到使弯矩绝对值最小的支座布置，即为该跨数条件下连续梁的最佳支座布置。

N＝1～ 4 时最佳支座布置如表1所示，由表1可知，最佳跨度均遵循连续梁中心轴对称的特点，因此对于N＝5～7 采用对称结构取半然后采用力法进行分析，当N＝7 时取一半结构，此时待定支座反力数为3 个，待定跨度数为4 个，极大地提高了搜寻效率。

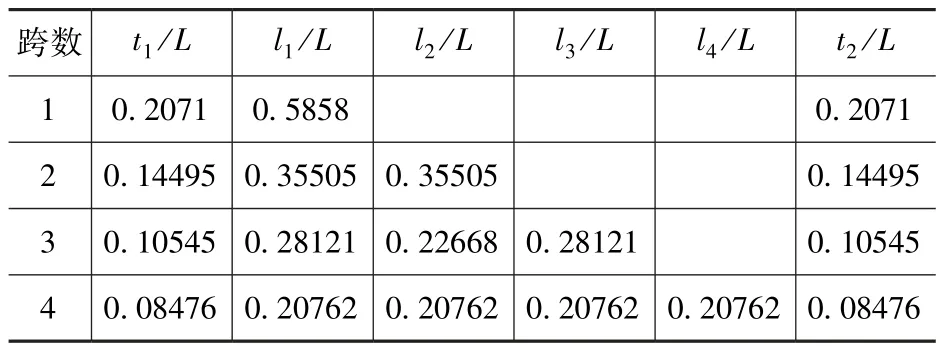
表1 N=1～4 时连续梁弯矩绝对值最小支座布置Tab.1 Optimal arrangement of continuous beam with span number N＝1～ 4

2 带悬挑连续梁最佳支座布置

2.1 1～7跨连续梁最佳支座布置

1.定性分析

均布荷载作用下，每跨梁内最大弯矩与该跨跨度及支座弯矩有关，在连续梁总长及跨数确定的情况下，在梁两端悬挑一定长度可减小跨度，同时悬挑端的支座弯矩可减小临跨跨中弯矩。以单跨为例，简支梁跨度为a，均布荷载为q，无悬挑时跨中最大弯矩为qa2/8，两端悬臂长度为b时(qb2/2 ＜qa2/8)，跨中弯矩为(qa2/8-qb2/2)＜qa2/8，因此从定性分析的角度来说，在连续梁两端适当悬挑一定长度，可减小梁内最大弯矩。

2.定量分析(N＝1～7)

在两端有悬挑条件下，前面采用力法已经计算给出了跨数N＝1～4 时连续梁的最佳支座布置(见表1)，当跨数分别为5、6 和7 时，取一半对称结构进行分析，对应的支座反力未知量数2、3和 3，长度未知变量数分别为 3、3 和 4 个，按照不同跨度条件下梁内弯矩绝对值最小的原则进行搜索，取梁总长L＝10m，均布荷载q＝1000N/m，得到跨数N＝1～7 的最佳支座布置如图2所示。

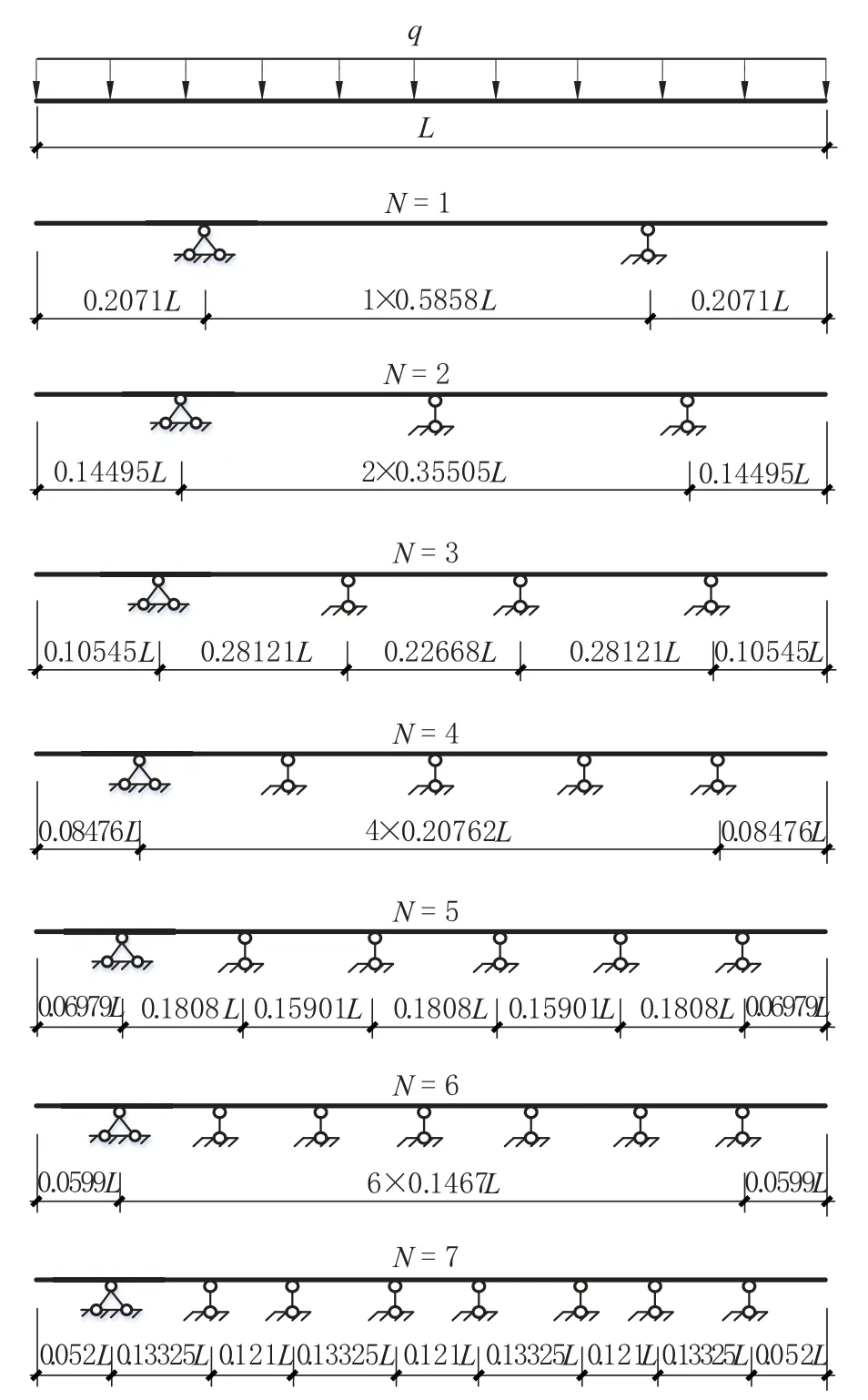
图2 N＝1～7 跨带悬挑连续梁弯矩最小支座布置Fig.2 Optimal arrangements for continuous beam with span(N＝1～ 7) based on minimum moment in beam

根据图2可以看出，最佳支座布置有以下特点：

(1)连续梁最佳支座布置仅与相对支座间距(支座间距/总梁长)有关；

(2)所有最佳支座布置均沿梁中心对称；

(3)当跨数为偶数时，支座间距相等；当跨数为奇数时，奇数跨跨度(l1，l3，l5，l7)相同，偶数跨跨度(l2，l4，l6)相同，且奇数跨跨度大于偶数跨跨度即l1＝l3＝l5＝l7＞l2＝l4＝l6；

(4)最大弯矩一般都出现在支座处，而非跨中。

可以看到，随着跨数的增加，奇数跨跨度与偶数跨跨度越来越接近，说明随着跨度的增加，弯矩最小连续梁支座布置越来越趋于等间距布置。

2.2 等间距支座最佳支座布置

根据图2可知，随着跨数的增加，最佳连续梁支座布置越来越趋近于等跨悬挑布置，等跨悬挑梁跨度变量更少，求解更方便，带悬挑等跨连续梁计算简图如图3所示。

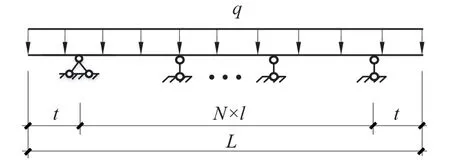
图3 悬挑等跨连续梁简图Fig.3 Sketch of continuous beam with overhang and identical span

1.1～7 跨等跨悬挑连续梁优化布置

对于带悬挑等跨连续梁，通过分析，可得到梁内弯矩最小的支座布置方式，如图4所示，其中当N为偶数时，与带悬挑连续梁最佳支座布置相同。

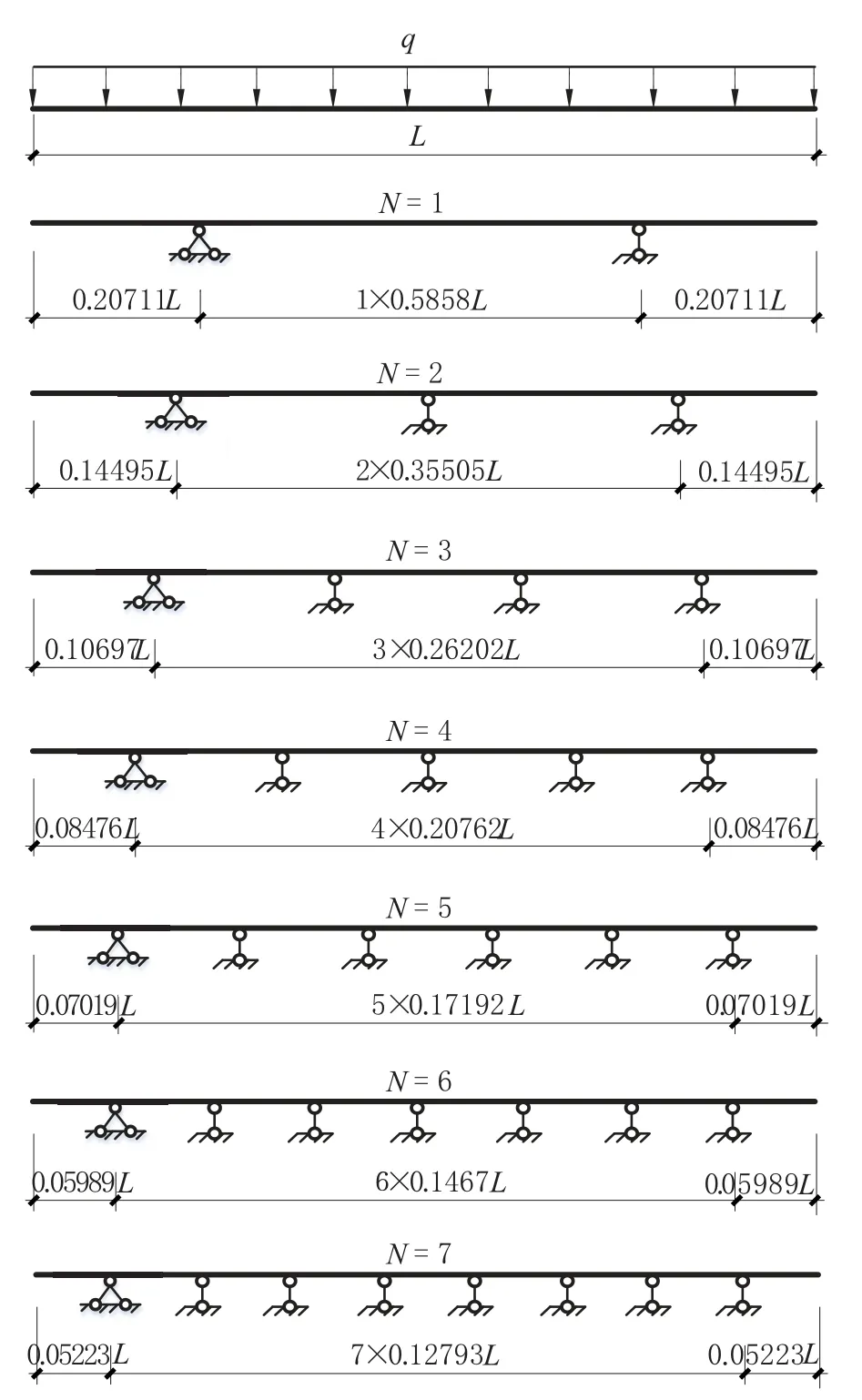
图4 1～7 跨带悬挑连续梁等跨度弯矩最小支座布置Fig.4 Optimal arrangements for continuous beam with overhang and identical span (N＝1～ 7) based on minimum moment in beam

2.N跨(N≥2)等跨连续梁优化布置

对于带悬挑等跨连续梁，无论跨数N为多少，支座布置需要两个值：悬挑长度t及跨中长度l，对于图4中t和l的关系进行对比，见表2。

表2 等跨悬挑最佳布置连续梁悬挑长度(t)与跨度(l)关系Tab.2 Relationship between overhang and span (t/l) for continuous beam with identical span

可以看到，当跨数N＝2～7 时，连续梁等跨度弯矩绝对值最小优化布置时悬挑长度与跨度间距之比(t/l)均为0.40825，故可推断N≥2 时带悬挑等跨布置连续梁弯矩最小支座布置方式为：

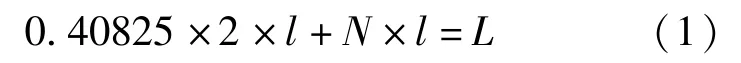
即跨度：

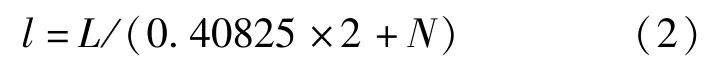
悬挑长度：

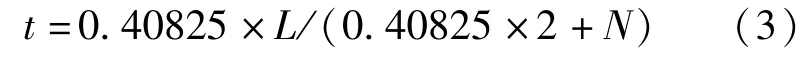
式中：L为连续梁总长度(m)；N为连续梁跨数(N≥2)；l为等跨连续梁跨度(m)；t为悬挑长度(m)。

3 无悬挑1～7跨连续梁支座布置

当连续梁两端无悬挑时，给定长度及支座数的连续梁内力与支座位置相关，通过分析不同支座位置，得到不同的弯矩分布。

3.1 无悬挑1～7跨连续梁最佳支座布置

无悬挑条件下连续梁最佳支座布置可取悬挑长度为0，通过计算，得到无悬挑条件下的1～7跨连续梁最佳支座布置如图5所示。

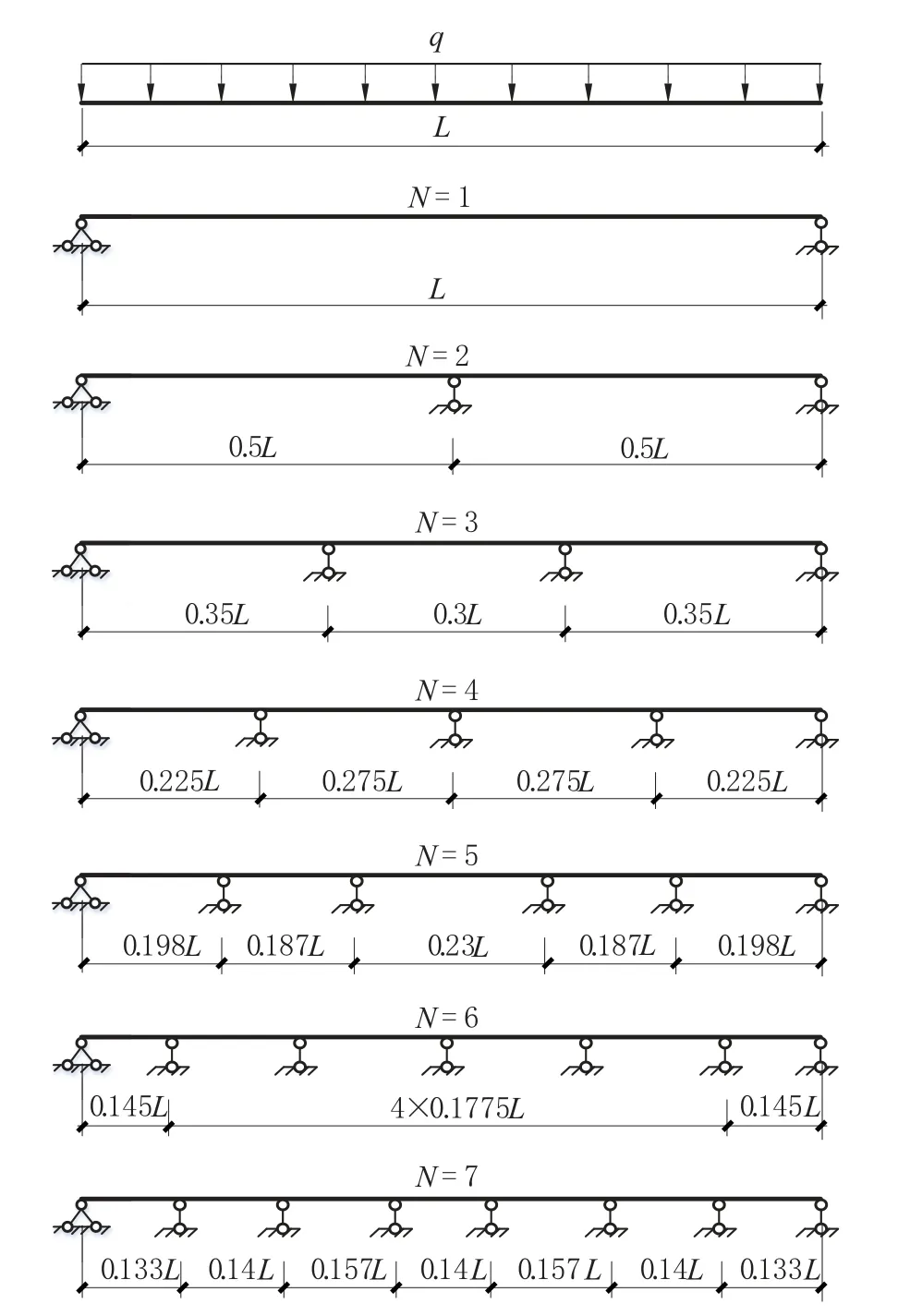
图5 1～7 跨无悬挑连续梁弯矩最小支座布置Fig.5 Optimal arrangements for continuous beam without overhang (N＝1～ 7) based on minimum moment in beam

可以看到，无悬挑条件下，最佳支座布置仍旧是对称的，但对于偶数跨，最佳布置时支座间距并非是等间距，当N＝3 时，结果与参考文献[9]得出的结论是一致的。

3.2 等间距布置

对于无悬挑连续梁，采用等间距支座布置时，布置方式只有一种，即跨度l＝L/N，此时连续梁内最大弯矩不小于无悬挑最佳支座布置时的最大弯矩。

4 对比分析

前面2、3 节给出了四种常用连续梁在梁内弯矩绝对值最小原则下的布置方式：悬挑最佳、悬挑等间距最佳、无悬挑最佳及无悬挑等间距布置方式，假设支座布置不受其他条件限制，对比这些支座布置间的差异，对于工程中连续梁的优化有重要意义。

梁总长L＝10m，均布荷载q＝1000N/m，图6给出了四种不同支座布置时2～7 跨连续梁内最大弯矩的对比，可以看到，有无悬挑，对连续梁最大弯矩影响较明显，但随着支座个数的增加，带悬挑支座和无悬挑支座连续梁内最大弯矩差距在减小，且对于有悬挑最佳和有悬挑等跨最佳布置，当N≥4 时两者差距不大；对于无悬挑连续梁，最佳支座布置和等间距支座布置导致的弯矩差值几乎不受跨数影响。

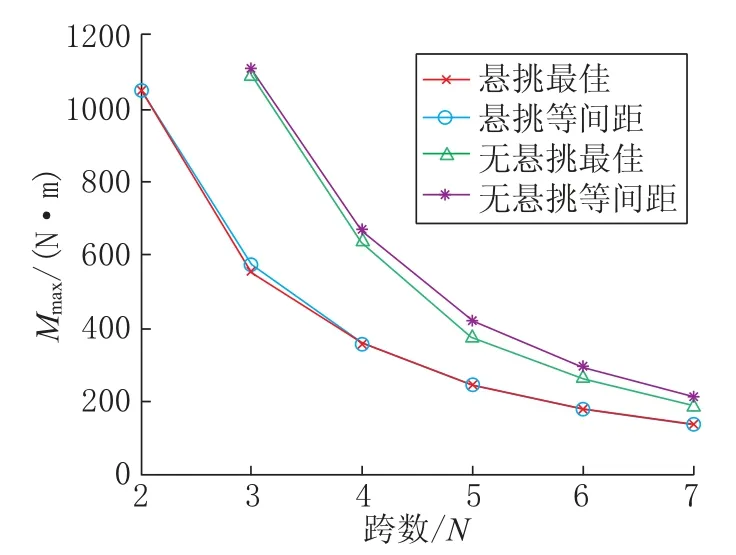
图6 不同跨数时支座优化布置时连续梁内最大弯矩Fig.6 Maximum moment in continuous beam under different arrangements of seat

表3详细列出了1～7 跨连续梁在四种支座最佳布置条件下的最佳支座位置及对应的最大弯矩值，需要注意的是，连续梁内力分布与相对跨度lN/L有关，而与绝对值lN无关。因此对于任意跨度L，根据表3即可求得各跨对应的最佳跨度布置值lN(N＝1，2，…，7) 和悬挑长度t1、t2值。

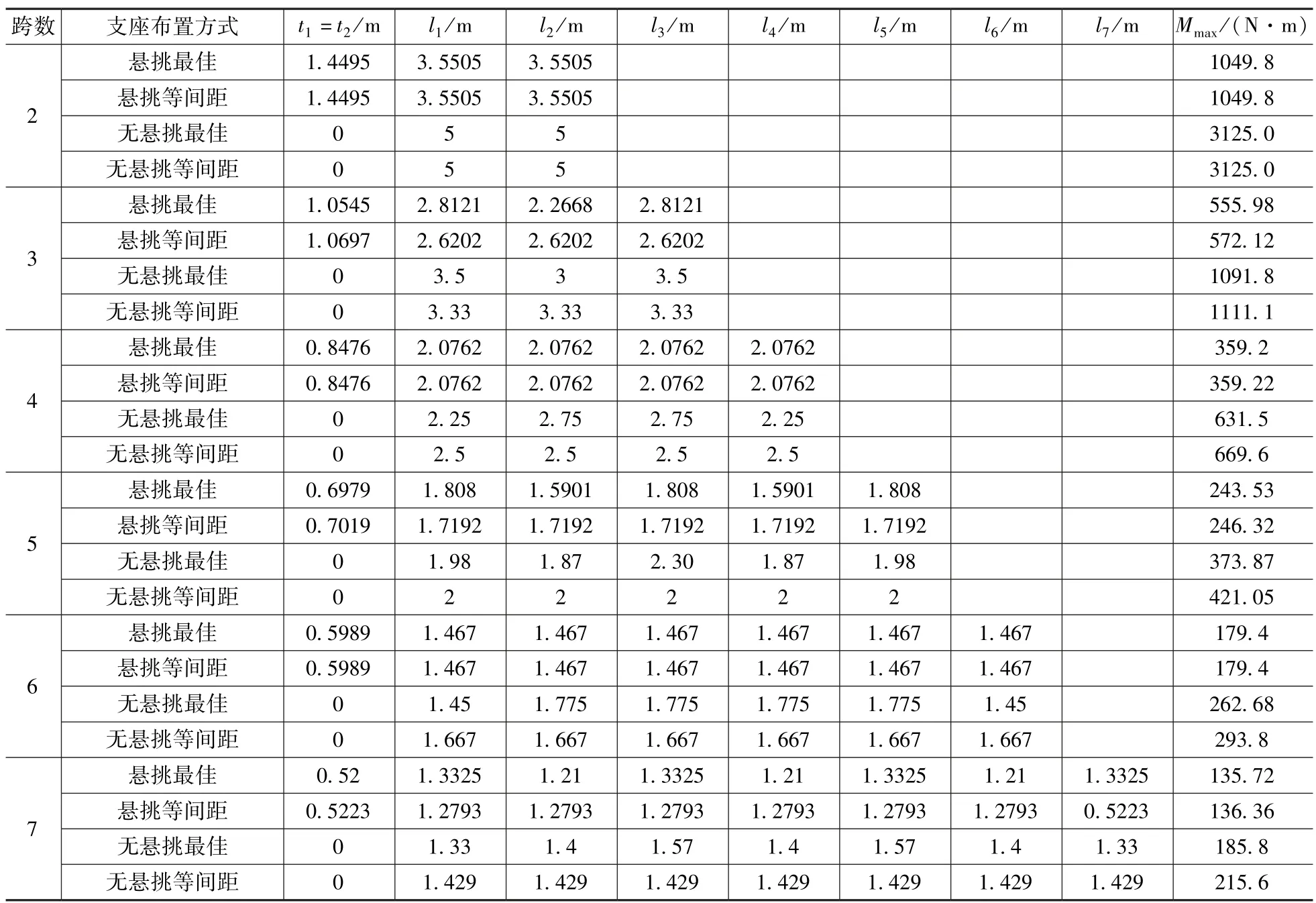
表3 N=1～7 跨连续梁不同支座最佳布置及最大弯矩Tab.3 Optimal arrangements of seat and maximum moment in continuous beam under different conditions(N＝1～7)

5 工程应用

连续梁在工程中应用广泛，这里列举两种常用连续梁形式，分别为光伏支架檩条和连续梁桥，前者可以采用两端悬挑的结构形式，利用带悬挑最佳连续梁布置的结论；后者一般不采用悬挑端，当采用等截面钢梁或者对称配筋混凝土梁时，可以利用本文中的无悬挑最佳连续梁布置的优化结果以实现支座优化布置。

5.1 光伏支架挑檩条—有悬挑连续梁优化

光伏支架是光伏组件的支撑结构，一般采用冷弯薄壁型钢结构，其结构特点是单个组串结构数量大，组串确定结构布置后，将大量重复，而对于单个组串的支架结构而言，檩条的用钢量一般可占到50%甚至更多，因此优化檩条内力和截面，可以减小用钢量和降低成本。

作为对比，选取一个简单算例，采用图7所示的横排布置，采用4×5 组串布置，沿檩条长度方向布置5 块光伏组件，单块光伏组件长×宽尺寸为1956mm×992mm，组件功率为300W，檩条总长为：1956×5＝9780mm，支架选用三跨，即檩条为三跨带悬挑连续梁构件，每个支架包含5 根檩条，其中中间3 根檩条受力大于两边檩条，但考虑到安装方便，一般5 根檩条设计成截面相同构件。

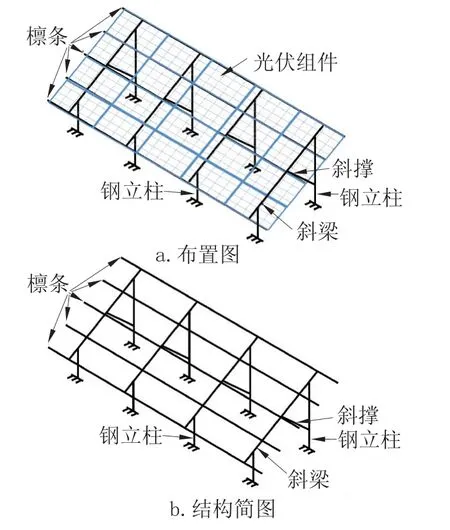
图7 光伏单组串(4×5)透视图Fig.7 Sketch of one set of PV mount system(4×5)

光伏支架荷载一般包括组件及支架自重、风荷载和雪荷载，这里自重荷载取0.2kN/m2，风荷载基本风压为 0.45kN/m2，雪荷载取为0.3kN/m2，进行荷载组合后，最不利荷载q＝1.2×0.2 +1.4×1.3×0.45 +1.4×0.7×0.3＝1.353kN/m2。

传统选择檩条跨度及悬挑长度时，跨距采用等间距，一般不超过3m，檩条悬挑长度一般不超过0.9m，这里为作为对比，选择等间距为2.7m，两边悬挑长度均为0.84m；而根据图2进行优化布置，此时悬挑长度为1.03m，中间跨度从左到右依次为 2.75m，2.22m，2.75m，在给定荷载工况下，檩条应满足强度、稳定性及挠度要求，檩条强度比均取0.9，计算得到两种支座布置条件下檩条用钢量对比如表4所示。

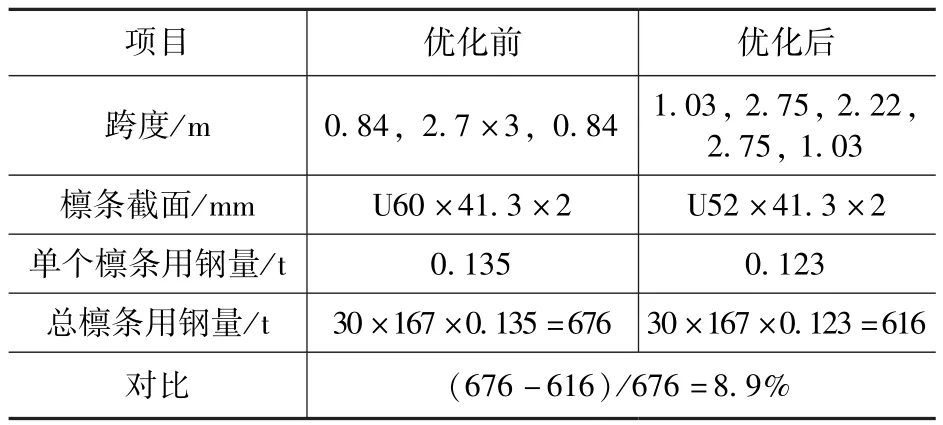
表4 檩条优化前后用钢量对比Tab.4 Comparison the consume of steel for purlin in PV mount

从表4中可以看出，在其他构件不改变的前提下，通过调整支座(立柱间距)位置，对于单个光伏支架组串，仅檩条一项即可节省12.2kg 钢材，考虑到光伏场光伏支架数目巨大，对于一个30MW 的光伏电站，约需要 5000 个组串，仅檩条一项，即可节省约60t 钢材，节省约8.9%的檩条钢材用量。

5.2 无悬挑连续梁桥—无悬挑连续梁优化

在桥梁工程中，当跨度较大时，采用简支梁桥则其跨中弯矩较大，结构自重大且不美观，一般情况下，可采用钢梁、混凝土连续梁、拱桥及斜拉桥等多种形式，在30m～160m 跨度范围内，混凝土连续梁受力合理，施工工艺成熟，具有较好的经济性。

混凝土连续桥包括带悬挑连续梁桥和无悬挑连续梁桥，前者一般适用于 40m～60m 桥梁，一般为三跨，两端跨悬挑，这类型桥由于牛腿施工复杂，且行车舒适度较无悬臂连续梁桥差，因此应用不及无悬挑连续梁桥广。对于无悬挑连续梁桥，如果采用等跨布置，则边跨跨中弯矩及支座弯矩较大，一般为了减小连续梁第1 跨跨中弯矩和支座处的负弯矩，通常是边跨小于中跨，连续梁边跨与中跨跨径比为边中跨跨径比，用α 表示，一般 α＝0.6～0.8。

无悬挑连续梁如图8所示，一般有3～6 跨，有变截面和不变截面两种，本处为了说明，采用最简单的不变截面、板式桥面，板厚度取为1m，连续梁跨数为5 跨，桥梁总长度为100m。

图8 多跨连续梁示意Fig.8 Sketch of continuous beam bridge

为分析不同支座布置及跨度对连续梁桥内力的影响，采用表3中无悬挑最佳支座布置和等间距支座布置及经验法给出的支座布置：

(1)无悬挑最佳支座布置跨度：从左到右依次为19.8m、18.7m、23m、18.7m 和19.8m。

(2)等间距布置则所有跨度均为20m。

(3)经验法推荐的跨距：常规连续梁的边中跨跨径比一般为0.6～0.8，中跨采用等间距，这里采用l1＝l5＝15.5m，l2＝l3＝l4＝23m，边中跨跨径比(l1:l2)为0.67。

根据《公路工程技术标准》 (JTG B01-2014)，整体设计时采用车道荷载，车道荷载由均布活载qk＝10kN/m，集中荷载Pk与跨度lN有关，跨度在 19m～ 28m 之间时，Pk在 236kN～272kN，跨度lN越大，Pk越大，这里统一取Pk＝250kN。

选取横向宽度为1m 的梁单元进行计算，恒载和活载产生最大跨中或支座弯矩时布置方式有差异，恒载在桥梁跨度方向满布，在求跨中最大弯矩时，该跨活载满布，再隔跨布置，集中荷载位于跨中；求活载产生最大支座弯矩时，活载满布在支座左右，然后隔跨布置，集中荷载布置在旁边跨中，恒载和活载作用下跨中及支座最不利布置如图9所示，图中跨中A 最大弯矩为图9a和b 叠加所得，支座B 最大弯矩为图9a 和9c 叠加可得。对于三种不同支座布置，计算得到板式单位宽度连续梁桥内最大弯矩见表5。

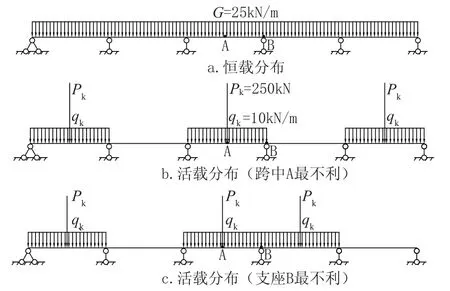
图9 五跨连续梁桥跨中及支座最不利荷载分布示意Fig.9 Load for middle span and seat in continuous beam bridge with five spans

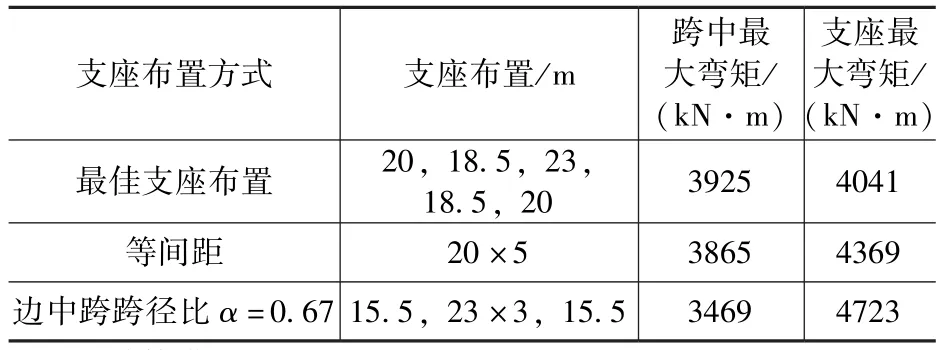
表5 不同支座布置条件下连续梁桥跨中及支座弯矩对比Tab.5 Moment in middle span and seat of continuous beam bridge under different arrangement of seat

由表5可以看到，等间距和无悬挑最佳支座布置在跨中弯矩方面差距不大，但最佳支座布置的支座弯矩较小，同时最佳支座布置对跨中及支座弯矩相差较小，说明内力分布较均匀；而当取边中跨跨径比为α＝0.67 时，跨中弯矩略小于最佳支座布置时的弯矩，但支座弯矩明显大于最佳支座布置时的弯矩。

考虑到混凝土梁抗弯承载力并非只与梁截面几何尺寸有关，而是会随着上、下截面配筋量大或小而增或减。当截面采用对称配筋或钢梁时，则配筋应按照截面正、负弯矩的最大值进行配筋计算，本文优化布置方法将有较好的适用性。

6 结论

通过研究均布荷载作用下连续梁支座布置对连续梁内最大弯矩的影响，给出了1～7 跨连续梁带悬挑最佳布置方式、带悬挑等间距最佳布置方式、不带悬挑最佳支座布置方式和不带悬挑等间距布置方式进行对比，可用于不同应用条件下的连续梁支座布置；将分析结论用于工程实例，表明连续梁支座经过优化后，可大幅减小连续梁内弯矩，主要结论有：

1.对于带悬挑连续梁，当跨数为偶数时，其最佳布置支座间距相等；当跨数为奇数时，奇数跨和偶数跨跨度各自相等。

2.当跨数N≥5 时，带悬挑最佳和带悬挑等间距最佳差异非常小；对于带悬挑等间距布置，当跨数N≥2 时，最佳支座布置时，悬挑长度t与支座间距l之比为0.40825。

3.随着支座个数的增加，带悬挑支座和无悬挑支座连续梁内最大弯矩差异减小，说明悬挑的影响随着跨数的增加而减小。