精心设计“问题链”，有效提高问题价值*—例谈初中数学问题链的设计原则

江苏省海门市东洲国际学校(226100) 江炜炜

问题是数学的灵魂,问题是知识的源泉,问题是思维的起点.在数学课堂教学中,问题是教学内容的生长点,也贯穿课堂始末的纽带,课堂中的每个问题并不是孤立存在,而是相互联系的.对于教师而言,精心设计教学中的每一个问题,串“问”成“链”,对提高问题的价值有积极的作用.笔者是一名初中数学教师,常年奋战在教学一线,对于问题链的设计及实施,笔者实践了多年,经过反复的改进与反思,笔者以为,设计有价值的问题链要始终坚持以设计原则为指导,下面结合实际谈一谈：

一、明确目标、有的放矢原则

教学目标是教学设计及实施的依据和准绳,因此明确目标、有地放矢是教师设计问题链时首先需关注的,从教学目标出发,围绕重难点有顺序、有梯度地设计问题,明确每个问题的设计目的.

如《14.4整式的除法》(人教版,下同)的教学重点是对单项式除以单项式及多项式除以单项式的运算法则的探索,在引入环节可以设置以下问题链：

问题1木星的质量约是1.9×1024吨,地球的质量约是5.08×1021吨,你知道木星的质量约是地球质量的多少倍吗?

问题2你觉得上述算法是否有点繁琐?你从式子和结果中能否发现某些运算规律,能使计算简单一点?

问题3计算(1)：( )·2a=8a3;8a3÷2a=( ).(2)：( )·3ab2=12a3b2x3;12a3b2x3÷3ab2=( ).

问题4观察上述后两个式子的运算,你找到了什么共同特征?

问题5你能尝试归纳单项式与单项式相除的运算法则吗?

设计意图首先由问题1的较大数据让学生体会到机械运算的“不方便”而激发对问题2的思考,再由问题3中已学过的整式乘法进行逆运算到问难4中规律的发现,最终上升到对问题5的探究.整个过程均围绕单项式除以单项式展开,逐层深入,目标明确.

课堂教学中问题应该都是经过斟酌与研磨过的,每个问题都承载着知识,所以设计问题要依据教学目标,让每个问题都有价值,避免“问无实质”和“问多无趣”的现象.

二、了解学情、因材施教原则

对学情的充分了解及掌握是教师进行教学预设所必须的,也是进行因材施教最直接的依据.问题链的设计是教学预设的主要内容,只有充分了解学情才能使问题更具有个性化,利于因材施教.

以《15.2分式的加减(2)》为例,在第一课时掌握了分式加减法运算法则的基础上进一步学会分式的混合运算,鉴于学生的接受能力及前一节内容的掌握情况,笔者设计了这样的问题链：

问题1计算并说说你的运算顺序.

问题2结合有理数的运算顺序,你能尝试说说分式的运算顺序吗?

问题3对于式子你觉得应该以怎样的顺序进行运算?

问题4试着计算上述式子,并说说在运算中你都注意了什么问题.

问题5你能再次总结分式的运算顺序并梳理其中需要注意的地方吗?

设计意图分式的混合运算在代数计算中属于难点,学生初学时会感觉比较困难,因此要循序渐进.问题1的设计是让学生回顾有理数混合运算的运算顺序,为本节课的内容做好铺垫,问题2是对自主学习的引导,让学生有主动探究的意识,在这个基础上尝试探究问题3及问题4,最后通过问题5再次对问题2的猜想进行补充与完善,从而初步完成该部分内容的构建.

“备学生”是充分备课的一部分,在教学设计中的问题链只有适合学生的认识水平及接受能力才能真正达到正确引导的目的,凸显教师主导、学生主体的实质.

三、引导探究、启发拓展原则

设计问题就是设计引导学生探究问题的方法,在提倡学生自主学习的当下,给每个孩子动脑筋的机会,充分挖掘每个孩子的潜力是非常必要的.因此问题链的设计可以以引导学生自主探究为主,同时适当设置延伸问题,给部分孩子提供探索的平台,启发孩子拓展思维.

如在《8.1二元一次方程组(1)》中对二元一次方程组及其解的概念构建环节,可以设置如下的问题链：

问题1下列方程组中,哪些是二元一次方程组?

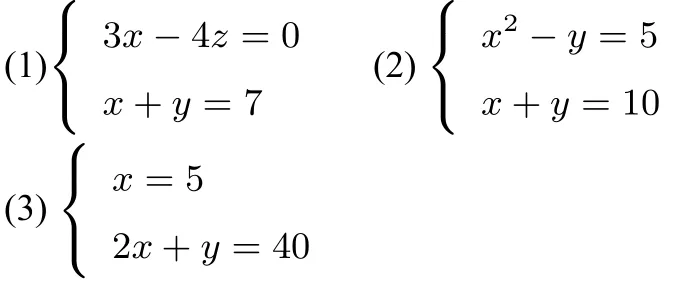
问题2你能用自己语言描述一下什么是二元一次方程组吗?

问题3你能不能猜想一下下列哪一组解是二元一次方程组的解?你为什么这样猜想?

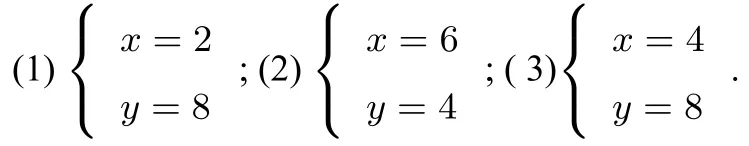
问题4你能用自己的语言描述一下什么叫做二元一次方程组的解吗?

问题5(选学)：用列举二元一次方程组的每个方程的解的方法来求方程组的解显然比较繁琐,能否找到简洁而可靠的方法呢?

设计意图二元一次方程组的第一课时以掌握二元一次方程组的定义及对其解的判断为目标,难度不大,因此以引导学生的自主探究为主.由问题1的具体问题到问题2的归纳、问题3的猜想到问题4的归纳,都由学生自主完成.问题5是对二元一次方程组解法的探究,实则为下一节课的教学内容,在时间允许的情况下展现给学生,但是不在课上解决,而是留至课后由学生自己探索解决,这样有利于激发孩子的探究欲望及学习的自主性,同时也可以为下一节课的内容做好铺垫.

四、注重梯度、循序渐进原则

对每个问题的难度把控是设计问题链时需要注意的,问题要从易到难、逐层加深,只有这样才能符合事物循序渐进的发展规律,体现出“链”的价值.

在《24.1圆有关的性质(1)》中,对圆的定义的应用环节有这样一个典型例题：

如图1,在Rt△ABC和Rt△ABD中,∠C=90°,∠D=90°,点O是AB的中点．求证：A、B、C、D四个点在以点O为圆心的同一圆上．

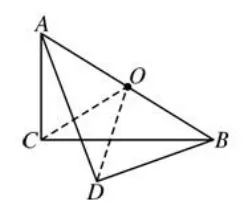
图1

可以设置这的问题链：

问题1什么是圆?

问题2如果给定一个确定的圆,需要你证明一个点在圆上,你有什么方法?

问题3如果要证明两个点同时在一个圆上,你有什么方法?

问题4如何证明四个点在同一个圆上?

设计意图本节课是新授课,同时也是章节起始课,学生独立解决这个问题是有一定难度的,需要教师的引导,将学生的思维打开.由问题1的设置是引导学生回归问题的本质,而后过渡到对问题2的探究,再由问题2逐渐加深到问题3及问题4,梯度明显,由浅入深,利于学生的接受.

问题链的重要价值之一在于它可以将一个个问题连接起来,使得问题相辅相成、环环相扣.问题不在于多,而在于精,问题的难度要始终控制在学生的“最近发展区”,使学生跳一跳够得到,这样的问题才是有意义的.

“教学有法而无定法”,在问题链的设计中,笔者认为上述几点原则是重要的,但并不是全面的,在今后的教学中,笔者会对问题链进行更深入的学习和反思,随时了解学科发展动向,争取以最新的理念设计每一节课,更好地服务于学生.问题好比一颗颗明亮的珍珠,教师要努力将这些散落在课堂每个角落的珍珠串联成美丽的项链,用心串联,使每颗珍珠都能发出璀璨的光芒,让每个问题都能发挥最大的价值.