是教会学生，还是让学生学会——一节市级小班化教学活动公开课的听后感

南京市大厂高级中学 陈业代

2019年4月,笔者参加了南京市高中小班化课堂展示汇报课活动,听了一节《点到直线距离》课,整节课学生小组讨论热烈,小组合作意识很强,答题踊跃,上台讲解大胆大方,让在场听课老师感到小班化教学与传统教学就是不一样．小班化的核心理念就是以生为本,关爱每一个,发展每一个,幸福每一个．它的总体目标是改变传统的教与学的方式,倡导自主、合作、探究学习,关注个体差异,引导构建平等、民主、合作、和谐的师生关系,促进每个学生全面而富有个性的发展．从该节课的教学效果来看,老师的教与学生的学基本到位,也可看出授课老师对“自主、合作、探究”领悟较好．但笔者认为在公式的推导这一环节上还可以再改进一些．

一、课堂实录

问题情境

师：生活中测量铁轨的宽度,人离高压电线的安全距离等等,都离不开我们数学上什么知识?

生众：点到直线距离．

(学生回答很快,因为问题一出来,老师就在投影仪上用PPT展示了本节课标题)

合作探究

师：如何求点P(3,0)到直线2x-y+1=0的距离?请同学们作出图像后思考有哪些计算方法?(全班33人,自然分成八个小组,分组讨论,2分钟后出现几个小组讨论热烈场面)

生1：我们小组的方法是过点P作直线2x-y+1=0的垂线,垂足为Q,先求出直线PQ的方程再与2x-y+1=0联立方程组求出点Q的坐标,运用两点间距离公式法求PQ的长即为点P到直线2x-y+1=0的距离．

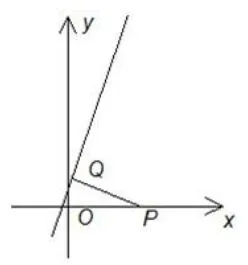
图1

图2

师：很好,这是运用我们上节课点点距离求解．其他小组还有不同方法?

生2：我们这组做法是利用等面积法求解,辅助线和第一小组一样,就是再过点P作x轴垂线交直线2x-y+1=0于点B,设直线2x-y+1=0与x轴交于点A,易算得AP、BP、AB的长,由·AP·BP可求出PQ的长．

师：太好了!这个办法就是构造“直角三角形斜边上的高”这个基本图形来解决的,从运算层面上看,好像比第一个方法更简单一点．其他小组呢?有没有不同方法了?

生3：我们这组也是用两点间距离公式,但与第一小组不太一样,不知道行不行?(这个学生有点胆怯)．

师：你说说看,让大家来评一评．

生3：就是设点Q(x,2x+1),PQ=,当时,PQ的最小值是．

师：同学们说说看,这个方法行不行?

生众：行!

师：这是运用构造目标函数法,这个方法不但行,而且也很好,因为······?

生众：计算不繁．

师：看来同学们都是认真思考问题的,下面给出这么一个问题,你能解决吗?

类比探究求点P(x0,y0)到直线Ax+By+C=0(A2+B2=0)的距离．

(自主探究、小组交流,8分钟后老师提问)

师：哪个小组先说说?

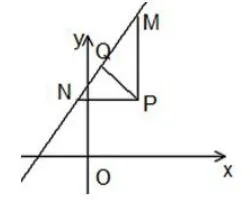
图3

师：很好,老师想问你,你们小组为什么不选用先求Q点坐标再利用求点点距离方法求解呢?

生4：那样的话,Q点坐标太难算了．

师：大家同意这位同学的说法吗?

生众：同意!

师：看来同学们都认真思考过了,学会了选择更佳方案(运算简单)解决问题．

师：其他小组同学还有没有更好的方案?第2小组?

生5：我们小组也是用等面积法的．

师：好的,看来用等面积法得到大家认同．(老师正准备接着讲下面内容,突然第6小组一个同学站了起来)

师：这组同学想很好,就是可想不可求啊,大家课后试试看．

接着老师展示点到直线的距离公式并交待注意事项,再接着就是数学应用即例题教学了(略)．

二、听课后一点感想与思考

1、学生自主了吗?

本节课的重点、难点就是“点到直线距离”公式的推导,授课老师采用由特殊到一般的方法,由学过的点点距离来探讨未知的公式,学生参与度比较高,老师留出时间让学生进行小组合作探究,学生通过动脑、动手,最后选出小组代表走上讲台利用实物投影给同学们展示小组合作成果,学生上课的积极性也能调动起来了,让现场听课老师感觉到学生学习能力很强．然而实际情况并非如此,笔者留心观察了周围四个小组,有三组未能推导出公式,只有一组基本推出来了,但仅是一个特别突出的学生一言论,其他同学是看客罢了．笔者认为,课堂教学要真正体现学生的主体地位,合作学习是建立在个体需求的基础上的,只有学生经过独立思考,有了交流的需要,合作学习才能有坚实的基础,这样的合作学习才会有成效.否则,在学生对问题还没有形成独立见解之前就急于讨论,由于学生的思维没有完全打开,就容易被别人的观点同化,造成人云亦云现象.所以,在合作学习前,特别重要的是要给予学生充分的时间以便独立思考．教师不要怕时间“浪费”得可惜,这恰好是培养学生良好的思维能力和运算能力最佳时机．

2、学生真合作了吗?

课堂上老师放手让学生去小组合作、探究学习是应该的也是必要的,关键是要给学生预留足够的时间去真合作、真探究,而实际上是老师一声令下,事先分好的小组一个个小脑袋凑在一起讨论了,仔细听他们讨论内容,基本都是在说过程、对答案,很少有同学问或讲出怎么想的?为什么这么做?这么做好处是什么?有没有其他更好的解决办法等等．笔者旁边的小组有个同学(生6)就是想用点点距离尝试,刚有一点头绪就被小组另外一个同学的思路打断了,这种合作探究,就无法让学生在探究中获得数学活动的经验,更谈不上提高学习能力了．由于教学时间的关系,教师给学生的合作时间不够．有的小组还未真正进入合作学习主题,有的才刚刚开始．这样的小组合作学习不但达不到合作学习的目的,而且很容易挫伤学生合作学习的热情,养成敷衍了事的不良习惯．另外,课堂教学中学生存在着差异,所以在学生开展小组合作学习的时候,教师应走到学生中间去,在组间巡视,关注学习有困难、默默不语的学生,让他们在老师与同伴的帮助鼓励下,积极地在合作学习中表现自我,从而获得成功的体验．

3、学生学会探究了吗?

在数学课堂上,倡导积极主动勇于探索的学习方式是高中新课标的基本理念之一,通过积极主动的探究活动使学生体验数学发现和创造的历程,可以培养学生的创新意识和创新精神,本节课主要是学生在老师预先设计的几个问题下进行学习的,教师为了完成本节课内容,用在公式的探究和推导上时间不够充分,多数学生没能在“规定”时间内推导出公式,即使有学生完成了推导,也是在老师铺设的“轨道”上进行的,没能训练出学生的思维量,学生主动探究意识不强,探究问题的深度可想而知了．作为老师要善于捕捉学生“意外”的问题,善待学生的质疑,处理好课堂预设与生成的关系,让学生在高效探究中自然生成有价值的知识和技能．本节课生6提出的问题,估计当时老师也是和同学一样想法,就用“课后去想想”搪塞过去了,让学生错过了一次有价值的探究活动,其实这时老师引导学生关注到中x,y并不是问题关键,关键是只要求出x-x0,y-y0即可,当A=0时,有由问题的结构特征可将等式化为设x0-x=Am,y0-y=Bm,代入上式得,因此．当A=0时,公式也成立．显然这样解决问题,抓住了问题的主要矛盾,寻找问题解决的突破口,这种思路体现了解析几何教学中的整体思想,是化繁为简的一种重要方法,也能突显探究问题思维的深度．

公式的推导证明是数学课堂教学的核心,教师要重视公式的推导,让学生理解并掌握公式的来龙去脉．作为教师,我们的任务不是教会学生,而是让学生通过自主学习获取知识,并领悟公式所包含的教学思想方法,灵活地掌握知识,应用知识,达到提高分析问题,解决问题的能力．