一维管单元模型确定裂隙岩体渗透张量的直接优化分析

王俊奇，薛振晓，穆孟婧

(华北电力大学，北京 102206)

裂隙岩体中的渗流影响到水利水电工程、石油工程、土木工程等稳定，还涉及核废料污染的防治、地下结构工程的排水、煤田瓦斯危害的防治、填埋垃圾的污水下渗和地下水资源的开发等。因此，研究裂隙岩体的渗透性规律具有非常重要的实践意义[1]。目前在岩体渗流的研究中，广泛采用的模型有：孔隙-裂隙双重介质模型、等效连续介质模型和离散裂隙网络模型。离散裂隙网络模型由于忽略了岩块本身的孔隙系统及裂隙岩体之间的水交替过程，用于岩体渗流分析更加简便，因此得到迅速发展[2]。

二维离散裂隙网络模型构造较为简单，发展成熟，已有学者在任意裂隙网络裂隙-孔隙渗流[3]、二维无压渗流[4]等方面做出尝试。而三维模型虽能相对精确地描述实际情况，但发展缓慢，目前在面状无限延展裂隙、任意裂隙渗流分析方面的研究已有一些成果[5- 6]。

即使离散型裂隙网络得到快速发展，但用以解决工程问题仍有很多困难，在解决实际工程问题时渗透张量表征渗透能力的连续介质有限元法仍是常用手段。确定渗透张量一般有物理试验法、理论解析法和数值方法。数值法方面，杨天鸿等[7]就二维裂隙网络尝试确定渗透张量；Baghbanan等[8]基于UDEC计算平台，考虑隙宽和迹长关联性研究二维渗透张量，确定REV。LEE I[9]在TOUGH2/ECO2N模型基础上，发展出一种离散裂隙网络DFN和非结构网格生成UMG模型，用以分析结构体中CO2的输运；吴锦亮等[10]生成尺寸不同的三维裂隙网络，采用复合单元法计算各向等效渗透系数，得到模型岩体的三维渗透张量和REV；李新强等[11]利用边界元法研究三维裂隙渗透张量；王俊奇等[12]基于一维管单元用遗传算法反分析尝试确定三维裂隙网络渗透张量。数值试验法在实际研究过程中成本较低，操作简单，可重复性高，是目前计算渗透张量的常用方法。

本文采用数值模拟方法，建立三维渗流模型，生成圆盘形三维裂隙网络，删除孤立和不连通的裂隙，将圆盘形裂隙网络简化为三维空间上的管单元模型网络。管单元的直径通过模型校正管径和隙宽比M的办法确定，即通过优化方法寻找适当的管单元直径，使计算获得的渗透张量值能够满意地拟合实测值。

1 离散裂隙渗流网络管单元模型与渗流解法

1.1 三维离散裂隙网络及研究域的生成

基于沟槽流假定，三维离散裂隙网络渗流发生在相互交错的裂隙圆盘内。根据裂隙圆盘由七个特征参数定义：裂隙圆盘中心的三维坐标x、y、z，裂隙圆盘的半径r，倾向α，倾角β，隙宽b。用蒙特卡罗法生成随机裂隙，形成三维结构面网络系统。为了保证渗流计算的合理性及减小计算规模，在生成域中选取一研究域立方体，祛除无用裂隙，再用深度优先搜索算法求得连通分量，最终确定有效研究域，如图1所示。

表1 裂隙岩体实测数据表

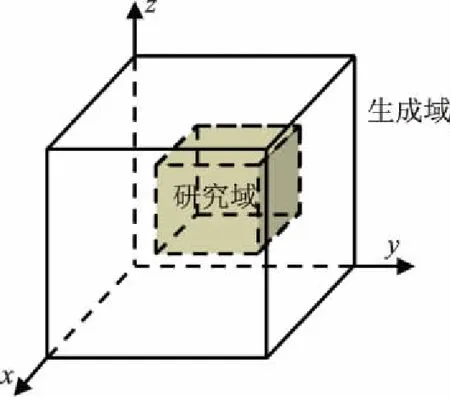
图1 研究域生成示意图

1.2 一维管单元模型

根据平面渗流假定，水在等厚度的整个圆盘平面内流动，有限元计算时需要划分平面网格，分析较大规模的实际问题就不太现实，研究表明[7]裂隙之间水的流动形态是以沟槽的形式流动，据此可以将三维裂隙网络简化成一维管单元进行分析。根据文献[6]建立管单元模型，研究域中相交裂隙产生交线，将交线中点与圆盘圆心相连形成一个管单元，渗流即表现为管单元通道中的水流。因管单元所属裂隙面的不同组对管单元分组，如图2所示。

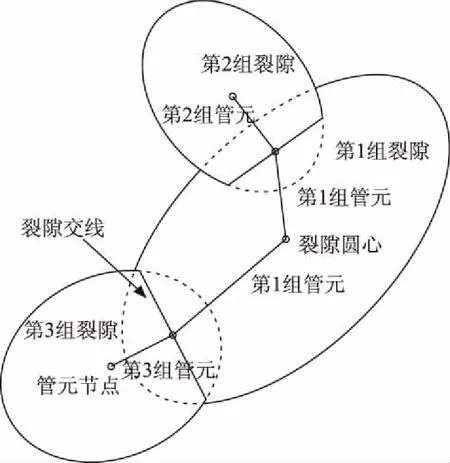
图2 管单元模型

建立了一维管单元模型后，根据文献[8]，可以对渗流区域内所有节点建立有限元方程组，表现成矩阵形式为：

[K]{H}={q}

(1)

式中，[K]—总渗透矩阵；{H}—节点水头的列向量；{q}—节点流量的列向量。

2 算例

2.1 裂隙网络的生成

根据文献[13]，查询获取实测的岩体裂隙数据，见表1。

本文自编渗流计算的有限元程序，输入已知的实测数据，生成100m×100m×100m的生成域，在生成域中心选取20m×20m×20m的区域作为研究域进行分析计算。研究域生成裂隙结构面1978条，其中第1组裂隙的结构面为1226条，第2组为402条，第3组为350条，将这三组不同的裂隙组分别用不同的颜色表示，如图3所示。将其简化为管单元后，研究域中有4104个单元，3303个节点，在研究域边界沿x方向，y方向，z方向分别施加定水头H1=30m，H2=10m，其余边界就为梯度水头边界，给定模型边界条件示意图如图4所示(施加ii方向的水头)，水头变化趋势如图5所示。

图3 研究域三组裂隙的结构面生成图

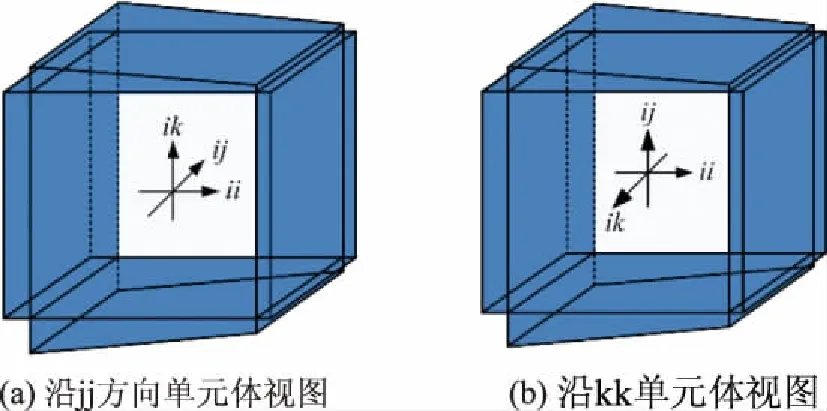
图4 计算模型的边界条件示意图

图5 裂隙网络的节点水头图

2.2 渗透张量的计算

模拟同一个野外实际入渗试验的岩体裂隙网络的渗流，施加如图4所示的水头边界条件，岩石的管径隙宽比M=D/b，其中D为管单元直径，b为裂隙张开宽度。每取一个M值，可以模拟出一个渗透张量矩阵：

(2)

设校准的的渗透张量矩阵为：

(3)

由于渗透张量矩阵的对称性，独立的数据只有6个。

设置目标函数：

(4)

为了得到适当的隙宽比使得计算出渗透张量尽可能地与标准渗透张量吻合，根据文献[14]经验，先取1～20的M值，求出f的值，将计算结果见表2。

表2 裂隙管径与隙宽之比和目标函数的对应关系

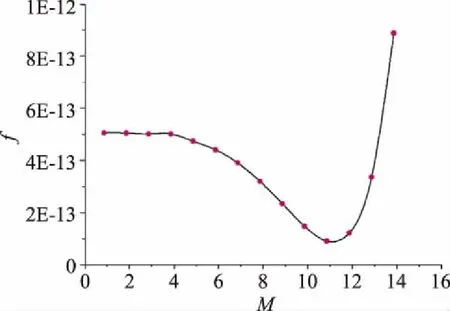
图6 M-f拟合曲线图(M=1～14)

将表2的数据绘制成M-f拟合曲线图可以看出，当M的取值在10到12之间的某一个数值时，f取得最小值，为了精准地求出f的极小值，在10到12之间再插入10个数据求出f的值见表3。

表3 隙宽比为10～12间对应的目标函数值

根据表3中所提供的数据画出以M为横坐标，以f为纵坐标的拟合曲线如图7所示。

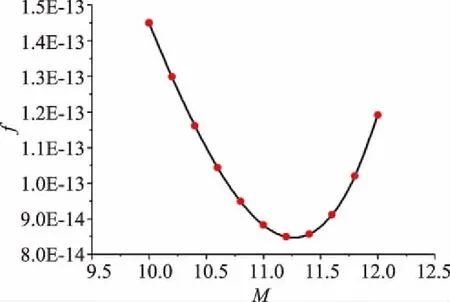
图7 M-f拟合曲线图(M=10～12)

得到拟合函数的趋势线为：

f=10-14(M3-40M2+400M-1000)

(5)

对求导可得：

f'=10-14(3M2-80M+400)

(6)

令f’=0，解得M=11.22，由此可得当管径与隙宽的比值为11.22时，函数取得极小值，即模拟得出的渗透系数与现场测量得到的渗透张量最为接近。权且称此法为直接优化的管单元模型，得到的渗透张量矩阵为：

(7)

继而得到如下相应的主渗透系数和主渗透方向：

(8)

根据文献[9]得到现场勘测的数据，采用边界元方法初步确定主渗透系数和渗透主方向，接着用现场压水试验进行校核，认为具有足够精度，最终得到以下相对精确的结果，本文采用管单元模型计算得到的渗透张量即是以这个计算结果作为拟合的标准进行比对验证：

(9)

用直接优化管单元模型计算出的结果式(8)与工程实例得到的结果式(9)相比，误差(ε为相对误差，θ为绝对误差)如下：

(10)

通过式(10)计算结果比较可以看出：求得的渗透主方向与实测岩体渗透主方向相差较小，不到30°；而求得的渗透主值与实测的渗透主值最大误差为0.61也在合理的误差范围内。

文献[14]具体操作中先做主方向的对比判断，再根据主值进行拟合，目标函数取为：

(11)

采用遗传算法反分析得到的管径隙宽比为M=11.5069，渗透张量计算结果如下：

(12)

(13)

遗传算法优化管单元模型计算出的结果式(13)与工程实例得到的结果式(9)相比，误差为：

(14)

3 结论

(1)一维管单元模型较于三维裂隙渗流网络结构更加简单，渗流计算所需的节点数和单元数更少，因而计算规模减小，为通过裂隙网络渗流确定渗透张量提供可行方法。

(2)通过给定一系列的管径隙宽比M，用直接优化方法计算出当比值M=11.22时，得到的渗透张量与实测的渗透张量相差不大，该比值从统计意义上认为可以用于确定裂隙网络岩体渗透张量。

(3)通过与遗传算法优化管单元模型得到的结果进行对比发现，在拟合渗透主值方面目标函数优化法更精确，在拟合渗透主方向方面遗传算法误差更小。