考虑初始损伤效应的重力坝动力体系可靠性研究

梁礼绘

(中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051)

混凝土坝在全生命周期中结构和材料性能都是随工作状态和环境不断变化的。主要表现为两个方面：一是混凝土本身由于材料特性等因素，不可避免地会有初始缺陷[1]存在(如空隙、微裂缝等)；二是岩石中节理裂隙等对岩石的变形和破坏特征产生不确定性影响[2]。特别是地震条件下，初始损伤状态使得结构对动荷载敏感性增强。当前时段重力坝系统损伤状态及其效应的影响不容忽视。因此，在评估坝体坝基系统抗震可靠性时，应当在结构系统的功能函数中考虑初始损伤状态的描述。

对于材料损伤描述而言：一种是通过唯象学模型以内变量的方法从宏观上处理损伤问题，借助有效应力的概念，将损伤状态以内变量形式引入到损伤状态方程；另一类方法是考虑微裂缝形成的物理机理，从微观力学角度导出材料的损伤方程。封伯昊等[3]利用损伤边界面的概念考虑结构损伤，引入可靠性分析中，进而分析结构安全性。目前，这一交叉领域的研究还处于探索阶段，对于考虑材料初始损伤状态的动力条件下坝体坝基体系抗震可靠性的研究还较少涉及。

本文研究对象是混凝土重力坝。通过引入损伤边界面和有效材料状态参量，分别考虑坝体混凝土和坝基岩体初始损伤效应，分别构造了包含损伤状态的重力坝混凝土和岩基的强度极限状态方程，在此基础上建立了重力坝体系抗震可靠度的分析模式。通过该分析模式，对某混凝土重力坝工程实例在初始损伤状态下的可靠性进行了分析研究。

1 考虑损伤效应的系统功能函数的建立

1.1 材料损伤状态及其效应的引入

混凝土材料初始损伤状态采用损伤边界面进行考虑。损伤边界面，是Fardis[4]研究混凝土损伤时提出的包络面，这一概念包含的应力空间可以用于描述混凝土在单调和循环加载下的损伤。采用Hsieh-Ting-Chen[5]提出的强调大主应力贡献四参数破坏面模型描述混凝土的破坏行为，同时考虑初始累积损伤量D0，取值区间[7]为[0，0.7]。对于本文算例：按照以弹性模量表征的损伤变量的定义，对于刚建成的坝体结构，混凝土的初始损伤为0.05左右，因此，在静力分析时取D0=0.05；动力分析中，根据文献[3]对水工混凝土进行的试验，应变在D0=0.3左右出现拐点，因此，取D0=0.3。本文暂不考虑动力荷载作用过程中的损伤演化情况。

其次，对于坝基岩体，引入有效材料状态参量来表征计算时段前的初始损伤状态。

损伤会使材料微观结构发生变化，从而进入新的材料状态[11]，造成材料特性随损伤而变化，发生变化的材料特性参数被称为有效材料状态参量[12]，例如岩石的有效弹性模量和有效破坏强度。文献[13]指出，损伤后的岩石材料强度就会随其损伤状态和应力状态而变化。根据文献[2]的研究，通过岩石样品裂纹产状的统计观测信息，发现岩石的损伤变量为满足[0，1]区间内的β分布。

1.2 功能函数模型的建立

混凝土材料破坏以受拉破坏为主，重点只考虑混凝土的受拉破坏[14]。对于重力坝结构，本文采用如下复合强度准则：坝体采用考虑损伤边界面的混凝土Hsiegh-Ting-Chen四参数破坏准则；基岩采用考虑材料等效损伤状态的Drucker-Prager准则。

将混凝土损伤边界面模型代入其破坏准则中，经变换，对应于初始损伤边界面的混凝土强度极限状态方程为：

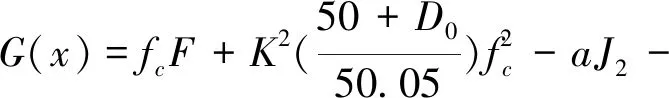
(1)

式中，F—主应力状态函数，根据不同的拉压组合有不同的形式。G(x)>0—可靠状态。

对应于考虑损伤效应DP准则的基岩材料的强度极限状态方程为

(2)

式中，各符号的含义如前所述，G(x)<0为可靠状态。

2 重力坝损伤体系抗震可靠度计算方法

本文研究的重力坝挡水坝段，其功能目标确定为对应于承载能力极限状态的强度安全和抗滑稳定安全，由于稳定问题归根结底是强度问题，因此重力坝整体可靠性归结为坝体和混凝土强度失效路径的体系可靠性。综上，重力坝体系抗震可靠度求解方法的思路为：首先，求解特定地震条件下的特定失效路径的失效概率；然后，考虑重力坝体系不同失效路径的相关性，求解其在特定地震条件下的体系可靠度；最后，考虑地震作用的随机性，基于全概率公式可以得到动力条件下的总失效概率及其可靠指标。

2.1 失效路径功能函数拟合及其失效概率

地震作用下重力坝的响应及失效函数与材料、荷载参数的关系十分复杂，且各变量之间多为非线性的隐式函数关系，如式(1)—(2)。因此，本文采用响应面拟合方法来模拟复杂的隐式函数。

在某特定地震动峰值加速度作用下，基于ANSYS中的可靠度PDS平台，借助APDL语言计入输入变量统计特性，首先采用振型分解反应谱法进行大坝系统动力条件下的随机有限元计算，得到重力坝系统应力场统计特性，进而采用响应面函数将式(1)—(2)统一表达为：

(3)

式中，n—随机变量的个数，a、bi、ci为待定参数。

这样，结构响应量的统计特性也被计入。根据C.G.Bucher和U.Bourgund[15]建议的方法，采用内插技术来确定待定因子。

最后，采用基于该响应面拟合方程，求得特定失效路径的失效概率，进而按照式(4)求解某个特定地震动条件下大坝系统的体系可靠度。

maxPfi≤Pf≤∑Pfi

(4)

式中，maxPfi—各失效路径完全相关的情况；∑Pfi—各失效路径相互独立的情况。

2.2 考虑地震随机性的全概率动力可靠度

特定地震动峰值下重力坝体系的失效概率，可以记为不同水平地震加速度系数条件下的失效概率，较难用精确的解析式表达，因此，通常采用数值拟合积法和全概率公式计算[16]得到总失效概率及其可靠指标。

(5)

β=Φ-1(1-Pf)

(6)

式中，f(A)—水平地震加速度系数的概率密度函数f(A)=Bbe-bA，A≥0，根据现有统计资料，暂取B=0.0499，b=19.948；Φ(•)—标准正态分布函数。水平向运动峰值加速度A与水平地震系数KH之间存在关系KH=A/g，其中g为重力加速度。

3 工程算例

某碾压混凝土重力坝，坝高149m。场地类别为一类场地。设防烈度100年超越概率2%水平峰值加速度为0.284g。竖向加速度代表值取水平向ah的2/3。在动力计算中取无质量地基，动水压按照Westergaard公式计算。考虑材料参数随机性，本文不考虑变异系数小于0.05的变量的随机性，将其视为确定性变量，同时离散化处理地震随机变量。各参数取值见表1，限于篇幅，只列出变异系数较大的变量。对于初始损伤状态，混凝土动力初始累积损伤量取为0.3，岩基的初始损伤由初始孔隙率折算[12]为0.09。

表1 随机变量统计特征值

3.1 失效路径的确定

参照文献[18]的研究，本文考虑地基中2条失效路径、坝体中3条失效路径，以及坝体地基间的一条交叉失效路径，共6种失效路径。对于前四条路径，将坝踵处坝体地基单元中可靠性指标最小的单元作为初始失效单元，采用逐步“杀死单元”的方法，搜寻下一个可能失效单元，进而找到可能出现的失效路径，直到失效路径上的累积失效概率不大于1.00%时，搜寻结束，并认为该路径已达到稳定[19]。

3.2 重力坝体系抗震可靠度

首先分析不同水平地震系数下各典型失效路径的失效概率。

基于响应面法的思想，将不同路径上单元强度的极限状态功能函数作为随机输出变量，采用ANSYS PDS模块进行随机有限元分析，分别拟合了失效单元强度的极限状态功能函数，并计算相应的失效概率和可靠度指标。

同时，重力坝体系可靠度属于串联体系可靠度问题，按照式(4)考虑各条失效路径之间的相关性，估算重力坝强度体系的可靠性及相应的失效概率的上下界限。进而得到不同水平地震系数下各典型失效路径及体系的失效概率，如图1所示。

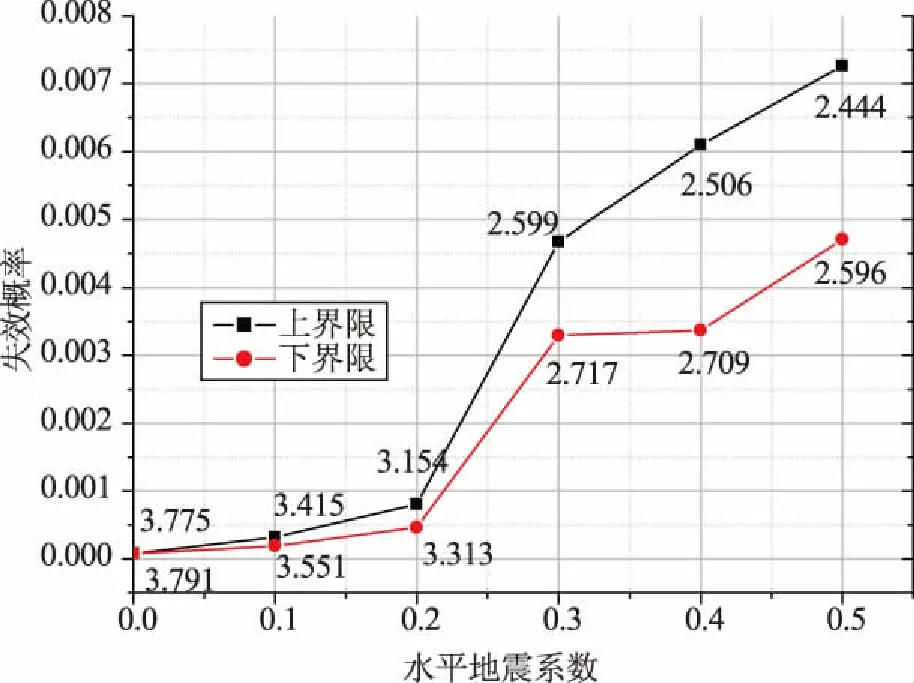
图1 不同水平地震系数下体系的失效概率

图2 不同水平地震系数与失效概率对数值的拟合曲线

由图1可知，不同路径的强度可靠指标随着水平地震系数的增大而减小；随着地震加速度的增大，坝体体系可靠度不再由建基面失效路径决定，而是由靠近坝顶的下游折坡处所在层面的失效路径决定，也体现了地震效应对坝体上部影响显著。本文以对数形式进行描述。对水平地震系数与失效概率上、下界限值的关系进行曲线拟合，得到的拟合函数，如图2所示，方程为：

(7)

式中，上界限拟合函数的参数为C=-4.08398，B1=4.3735，B2=11.5682，B3=-29.5566，B4=8.7709；下界限拟合函数的参数为C′=-5.1039，B′1=17.7353，B′2=-60.2762，B′3=126.1103，B′4=-108.8928。经检验，拟合函数在A=0～0.5的区间内拟合优度均接近于1。

将式(7)代入式(5)并进行A=0.5的右截尾计算，得到重力坝体系在地震作用下的失效概率为Pf=4.63011×10-6～1.0305×10-5，相应的可靠指标为4.258～4.433。

3.3 计入损伤与不计入损伤的对比

针对水平地震系数为0.2的情况，分别对大坝计入初始损伤和未计入初始损伤状态下的典型路径上单元强度可靠性进行分析，结果如图3—4所示。从图3—4可以看出：

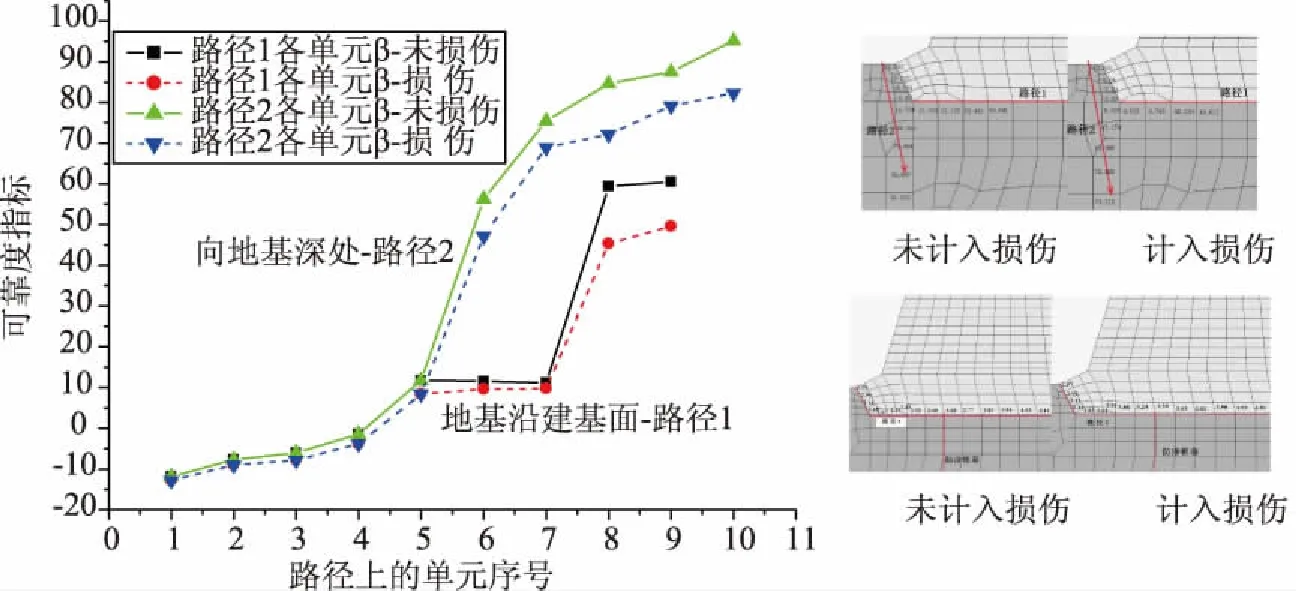
图3 不同初始状态下坝基失效路径单元强度可靠度

图4 不同初始状态下坝体失效路径单元强度可靠度

(1)两种不同的初始状态下，坝体可靠度与坝体应力的分布规律基本一致，混凝土坝体可靠度最低的区域均位于坝踵和下游折坡点单元；坝踵单元的可靠指标分别为β损伤=2.57、β非损伤=2.58；下游折坡点单元的可靠指标分别为β损伤=3.267、β非损伤=3.283。

(2)从数值上看，随着路径向坝体内部发展，单元的强度可靠性不断增大。坝踵区域，基岩材料单元强度失效概率远大于坝踵混凝土。即该条件下，坝踵区域的破坏首先出现在基岩内部并向地基深处发展。

(3)从坝体内部几条失效路径的单元失效概率来看，动力条件下，下游折坡处单元强度最先失效。

4 结论

本文通过引入损伤边界面和有效材料状态参量，分别构造了包含初始损伤状态内变量的重力坝混凝土和岩基的强度极限状态方程，并在此基础上建立了重力坝体系抗震可靠度的分析模式。实例分析表明，该分析模式使得在重力坝运行的特定时段的体系可靠性分析和评价更为合理，并能对混凝土重力坝在运行期内基于损伤演化特征的时变可靠度进行初步预测。主要得出了以下结论。

(1)以损伤内变量的形式，提出了考虑损伤状态耦合影响的混凝土四参数强度准则和岩体修正DP破坏准则，建立了混凝土和岩石材料含初始损伤效应的极限状态功能函数模型，并在此基础上建立了重力坝体系抗震可靠度分析模式。

(2)两种不同的初始状态下，坝体可靠度与坝体应力的分布规律基本一致。混凝土坝体可靠度最低的区域均位于坝踵和下游折坡点，在坝踵和坝踵与基岩的结合部损伤最显著，损伤区域从坝体与基岩结合部向坝体和基岩内部逐步扩展，并逐步向内减弱，同时，在坝趾处也发生一定程度的损伤。对于坝体区域，在动力条件下，下游折坡处单元强度最先失效。

(3)计入初始损伤后，重力坝在坝体地基交接处点可靠度下降较大；敏感性分析表明，在动力条件下，基岩弹模与地基单元强度失效负相关；坝体混凝土单元强度可靠性与基岩弹模负相关，与混凝土抗压强度正相关，且显著敏感性达到10%。即从可靠度的角度说明了坝头部位置换高标号混凝土有利于提高坝体抗震性能。