探究平抛运动与斜面结合问题的解题思路

■陈志宇

平抛运动是物体只在重力作用下以一定的水平速度v0抛出的曲线运动。平抛运动是水平方向的匀速直线运动和竖直方向的自由落体运动的合运动，运动时间t，水平方向的位移x=vxt=v0t，竖直方向的位移y=为平均速度，因为物体在竖直方向上做初速度为0的匀变速直线运动)，合位移s2=x2+y2;t时刻其水平方向的分速度vx=v0，竖直方向的分速度vy=gt，合速度。

图1

如图1所示，在0～t时间内的位移为s，速度的偏转角为θ，位移的偏转角为φ，则，因此tanθ=2tanφ。在t时刻合速度v的反向延长线与x轴的交点A是水平位移的中点，即。过O点作OC平行于AD，过A、D分别作OC的垂线，交点分别为B、C，那么线段DC的长度就是轨迹曲线与OC的最大距离h。由几何关系得AB=CD=h，∠AOC=θ，在△AOB中。

解决平抛运动与斜面结合问题的思路主要有四种：一是利用速度的合成和分解的方法进行求解;二是利用重力加速度、初速度分解进行求解;三是利用动能定理(机械能守恒定律)，并结合运动学公式进行求解;四是利用几何关系，以及解析几何知识进行求解。

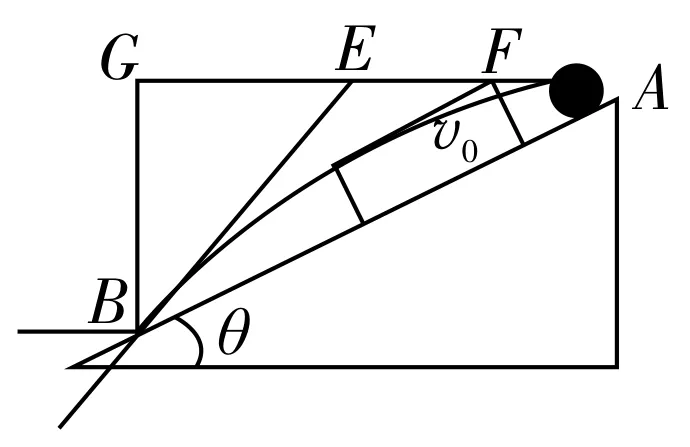
图2

例题如图2所示，在倾角为θ的斜面顶端A处以速度v0水平抛出一小球，落在斜面上的某一点B处，设空气阻力不计，求小球从A点运动到B点所需的时间、落到B点时的速度，以及A、B两点间的距离。若从抛出开始计时，则经过多长时间小球离斜面的距离达到最大?这个最大距离是多少?

解：利用平抛运动的基本规律。设经过t时间小球离斜面的距离达到最大，小球离斜面的最大距离为h，水平位移、竖直位移分别为x、y;t时刻水平分速度、竖直分速度分别为vx、vy;小球从A点运动到B点所用时间为T，水平位移、竖直位移分别为X、Y，A、B两点间的距离为sA B;小球到达B点时的速度大小为vB。

小球离斜面的距离达到最大时，tanθ=(此时合速度方向与斜面平行)，vy=gt，vx=v0。小球从A点运动到B点所用时间T=2t。联立以上各式解得。因为。小球到达B点时的速度的大小vB=。因为E、F分别是AG、AE的中点，所以由几何关系得。

说明：在求解t、T、vB时，可以以A点为原点，以斜面所在直线为x轴，以垂直斜面为y轴，建立直角坐标系，把v0和g沿x、y轴分解;在求解h时，可以以A点为原点，以水平方向为x轴，以竖直方向为y轴，建立直角坐标系，利用平抛运动规律、动能定理和几何关系列式求解，或者利用解析几何知识列函数关系式求解。感兴趣的同学不妨自己试试看。